全屏蔽阀门磁力驱动器驱动性能分析①

2018-01-29郭文君李双喜

化工机械 2017年6期

李莹王骁郭文君杜江李双喜

(1.北京化工大学机电工程学院；2.中国核电工程有限公司)

在化工、核电、航天及航空等领域中，对高放射性、剧毒性介质要求零泄漏[1]。磁力驱动器可以实现阀门动力端(驱动器)与工作端(阀杆)之间的全屏蔽隔离，利用磁力驱动阀门旋转，实现阀杆密封零泄漏，保证设备的安全稳定运行[2～4]。然而，磁力驱动器发热功率的增大会引起定子导体的温升，而过高的导体温升将烧损导体绝缘层，导致磁力驱动器失效[5]。目前的研究内容仅局限于磁力驱动器自身结构参数与工况参数的影响规律分析，缺少结合实际应用场合进行的研究。

为此，笔者结合大型液体火箭发动机阀门的运行工况特点，研制了一种全屏蔽阀门磁力驱动器。基于有限元磁场分析理论，对磁力驱动器内部磁场进行数值计算。研究阀门不同开度对应的负载力矩下磁力驱动器的力矩输出性能与发热特性，分析磁力驱动器结构参数对驱动性能的影响规律。设计并搭建动态负载试验装置，对不同阀门负载力矩下磁力驱动器的性能进行试验验证。

1 结构和工作原理

全屏蔽阀门磁力驱动器的整体结构如图1所示。该磁力驱动器定子通电线圈产生的磁场与转子永磁体产生的磁场相互作用，产生的电磁力矩通过屏蔽套无接触地传递给转子。转子通过传动键直接驱动阀杆旋转，实现阀杆全屏蔽密封条件下阀门的启闭功能。

图1 全屏蔽阀门磁力驱动器

2 磁场有限元模型

全屏蔽阀门磁力驱动器有限元模型不同区域的材料属性见表1，不同阀门开启状态下的载荷与边界条件见表2。

表2 载荷与边界条件

建立磁力驱动器有限元计算模型，采用三角形单元对模型不同区域进行网格划分，如图2所示。根据定子每相绕组电流的有限元计算结果，计算对应的力矩系数。以球阀启动状态、球阀开度为0%和球阀开度为20%对应的密封副摩擦力矩作为磁力驱动器的3种负载力矩工况，采用Ansoft Maxwell对磁力驱动器模型进行负载瞬态磁场分析，具体计算结果见表3。

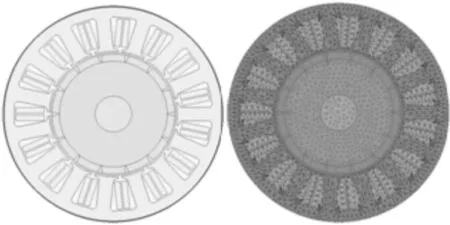
图2 磁力驱动器有限元模型与网格划分

项目球阀启动球阀开度为0%球阀开度为20%负载力矩TL/N·m20.6710.345.09定子绕组相电流I/A2.091.040.51力矩系数KT/N·m·A-19.869.899.92发热功率Pcu/W270.2866.9216.09

由于定子绕组相电流随着负载力矩的增大而增大，因此磁力驱动器内由绕组导体产生的感应磁场的磁场强度也相应增大。当该磁场强度增大到一定值后，磁力驱动器会出现局部磁饱和的现象，使得磁力驱动器的磁阻增大，工作磁通减小，力矩系数减小。在相同结构参数下，磁力驱动器的发热功率与其绕组相电流的平方成反比关系，因此发热功率随着负载力矩的增大而迅速上升。

3 驱动性能分析

全屏蔽阀门磁力驱动器的主要性能参数包括力矩系数KT和发热功率Pcu[6]，计算式如下：

(1)

(2)

其中，a为定子绕组导体并绕支路数，Φ为磁力驱动器的工作磁通，N为定子绕组导体根数，R为定子绕组电阻，ρcu为绕组导体材料的电阻率，Lw为绕组导体总长度，qcu为绕组导体裸线截面积。由式(1)、(2)可知，在一定阀门负载力矩下，力矩系数越大，磁力驱动器定子绕组所需的电流载荷越小，磁力驱动器的力矩输出性能越好。而且，减小发热功率可降低导体绝缘层烧损的危害，提高磁力驱动器在阀门驱动过程中的工作可靠性与安全性。磁力驱动器的工作磁通是影响其驱动性能的重要参数，而屏蔽套、定子和转子的结构参数对工作磁通均有显著影响。

3.1 屏蔽套结构参数

影响磁力驱动器力矩输出性能的屏蔽套结构参数为屏蔽套厚度。采用Ansoft Maxwell对磁力驱动器进行空载工况下的瞬态磁场分析。保持其他结构参数不变，不同阀门开度下屏蔽套厚度对磁力驱动器的力矩系数和发热功率的影响如图3所示。可以看出，随着屏蔽套厚度的增大，工作磁通减小，力矩系数减小。同时，随着阀门负载力矩的增加(阀门开度的减小)，由导体电流感应的磁场逐渐增强，使定子铁芯发生磁饱和，导致磁力驱动器的工作磁通减小，力矩系数减小。随着屏蔽套厚度的增大，发热功率成线性增长趋势，且随着负载力矩的增大，发热功率增长幅度变大。

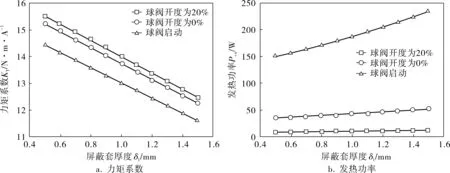
图3 屏蔽套厚度对力矩系数和发热功率的影响

综上所述，为提高磁力驱动器的驱动性能，应减小屏蔽套厚度。但屏蔽套作为阀门的承压件，其厚度决定着阀门的承压能力。因此设计时应综合考虑以上两点因素，选取合适的屏蔽套厚度。

3.2 转子结构参数

转子结构参数(永磁体极弧系数和永磁体厚径比)影响磁力驱动器的工作磁通，进而影响其力矩系数和发热功率。永磁体极弧系数αi和永磁体厚径比Kmr的表达式如下：

(3)

其中，p为转子永磁体极对数，bm为永磁体外圆弧长，Dro为转子外径，δm为永磁体厚度。在磁力驱动器空载工况下进行瞬态磁场分析，提取不同极弧系数和厚径比下的磁力驱动器磁通密度，并进行傅里叶分解，得到对力矩系数和发热功率的影响规律如图4、5所示。

可以看出，力矩系数随极弧系数和厚径比的增大而增大，增大趋势逐渐减缓，发热功率呈先减小后趋于平缓的趋势。当极弧系数和厚径比相同时，由于磁饱和的出现，使得磁力驱动器的工作磁通随着阀门负载力矩的增大而减小，导致力矩系数减小，发热功率增大。

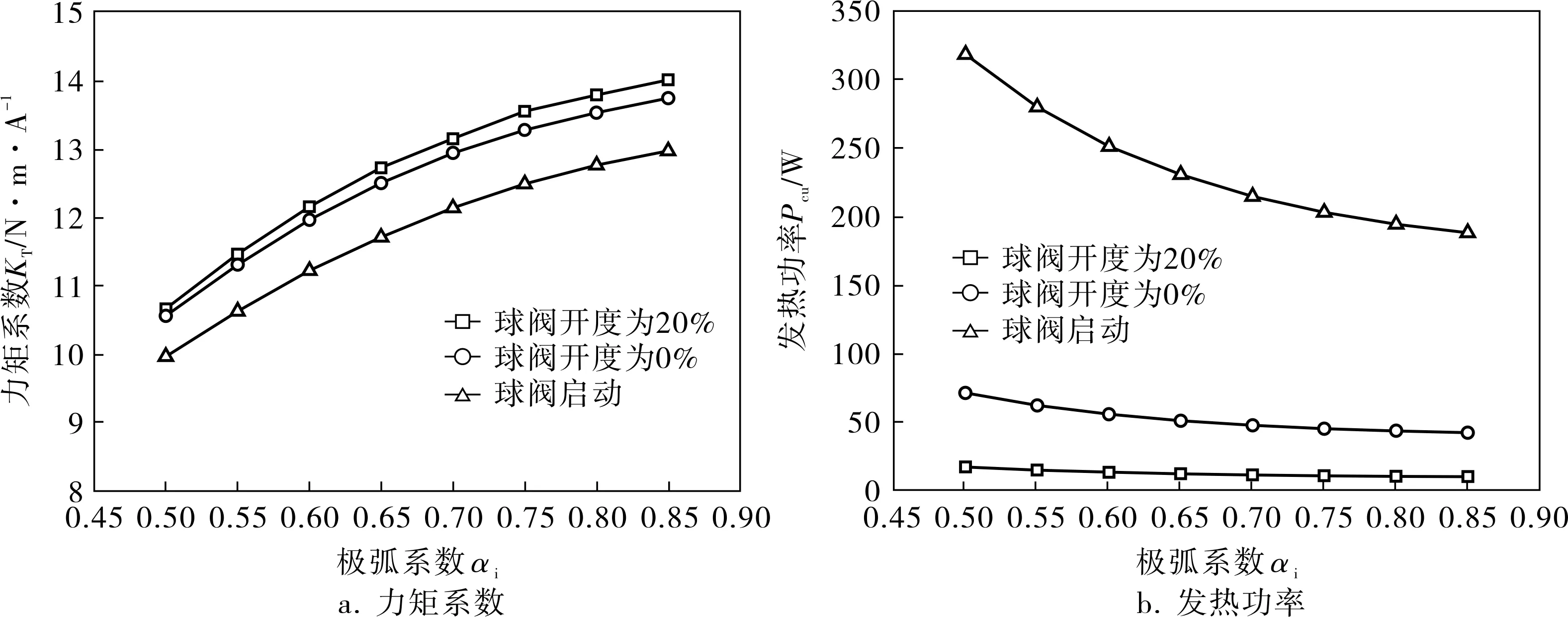
图4 极弧系数对力矩系数和发热功率的影响

图5 厚径比对力矩系数和发热功率的影响

3.3 定子结构参数

影响磁力驱动器力矩输出性能与发热性能的定子结构参数有定子内径Dsi、定子外径Dso、槽顶宽bs2、齿宽bt、槽高hs3和轭高hy。齿槽宽比Kts、定子裂比Ksp和槽轭高比Ksy的计算式如下：

(4)

其中，Rs为槽底圆弧半径。在不同阀门开度下，齿槽宽比、定子裂比和槽轭高比对磁力驱动器力矩系数和发热功率的影响规律如图6～8所示。由于齿槽宽比、定子裂比和槽轭高比的增大均使磁力驱动器出现局部磁饱和现象，故力矩系数存在最大值。当力矩系数较大时，在相同负载力矩条件下，由于定子绕组相电流较小，因此发热功率存在最小值。可见，在球阀设计中必须重点考虑齿槽宽比、定子裂比和槽轭高比对力矩系数和发热功率的影响，防止力矩不足或发热功率过高引起的定子绕组线圈烧损等问题。