基于指数曲线法沉降预测模型的在役储罐疲劳寿命分析①
2018-01-29陈志平苏文强唐小雨范海贵
程 健 陈志平 苏文强 唐小雨 范海贵
(浙江大学化工机械研究所)
随着国家石油战略储备基地和商业油库的建成,大批储罐都已经投产进油,保障这些在役储罐的安全运行意义重大[1,2]。由于工业发展和战略布局的需要,储油罐大部分建造在沿海的软土地基上。储罐地基土层复杂,泥土压缩性能不相同,储罐运行时液位变化引起地基应力场的改变,很容易导致储罐地基发生不均匀沉降。地基的不均匀沉降有可能会使局部结构产生很大的峰值应力,并在物料周转过程中储液升降的循环载荷下发生疲劳破坏,引起重大安全事故。
国内外学者对储油罐在沉降下的结构安全性做了大量的研究工作。傅强等基于弹性基础力学模型分析了储罐的结构应力,表明基础不均匀沉降会导致储罐底板、大角焊缝等部位受力复杂化[3]。赵阳等研究了储罐结构性能与沉降的关系,表明罐周不均匀沉降对其结构的影响最为不利[4,5]。Mousa E A和Ruiz C采用理论分析和实验模拟相结合的方法研究了储罐在不均匀沉降下的应力变化,并指出不均匀沉降过大将导致储罐大角焊缝结构发生破坏[6]。程香等采用有限元分析技术对大型油罐在某个沉降值下的疲劳寿命进行了预测分析。国内外学者尚未对储罐发生不均匀沉降后服役过程中的结构疲劳问题开展研究[7]。笔者根据在役储罐地基实测沉降数据,建立指数曲线法沉降预测模型来预测储罐在役过程中不同时刻罐周各沉降点的沉降值,采用储罐-地基接触有限元方法预测分析储罐的疲劳寿命。
1 沉降预测模型
1.1 指数曲线法沉降预测模型
指数曲线法是一种基于实测沉降数据来预测地基沉降量的方法。其核心为地基固结沉降公式,该公式由曾国熙和杨锡令根据受压层的固结度公式,并参照尼奇波罗维奇的第二公式推导而得[8],后经简化作为预测地基沉降的经验公式之一[9,10],表达式如下:
St=(1-αe-βt)S∞
(1)
其中,St表示在时间t时刻地基的沉降量;t表示地基沉降时间;S∞表示待定的基础最终沉降量;α和β为待定系数,均为正值。对待定参数的求解,需要根据地基不同时间段的实测沉降数据,绘制沉降-时间散点图,进行拟合求解。
但因式(1)包含自然常数e,直接拟合难度大、精度低,因此将式(1)转换成以下函数形式:
(2)
式(2)中,各参数意义不变,只是将St转换成关于1/et的函数。把1/et作为沉降关系曲线的横坐标,St作为纵坐标,根据储罐地基各时刻的实测沉降数据绘制1/et和St的沉降关系的散点图,在MATLAB中对散点图进行拟合求解,即可得到地基沉降-时间预测公式,如图1所示。
1.2 实测沉降数据下预测模型的验证
以文献[11]中记录的1050号油罐基础沉降实测数据图为例,利用油罐6号沉降观测点的实测数据验证该沉降预测模型的准确性。1050号油罐正式投产进油后地基6号沉降观测点的实测沉降数据见表1。

图1 沉降经验公式拟合曲线

表1 1050号油罐地基6号沉降观测点实测沉降数据
注:*取储罐正式服役起始月为0月。
分别采用表1中前6、9、12个实测沉降数据点,将数据中的时间t转换成1/et(t以年为单位)后,对应的沉降实测值不变,绘制沉降-时间散点图,进行沉降指数曲线经验公式拟合法求解。得到了式(3)~(5)的沉降-时间预测公式:
S6t=(1-0.3334e-1.242t)×1067
(3)
S9t=(1-0.3144e-1.359t)×1037
(4)
S12t=(1-0.3226e-1.195t×)1054
(5)
图2为相应的预测曲线与实测数据对比。
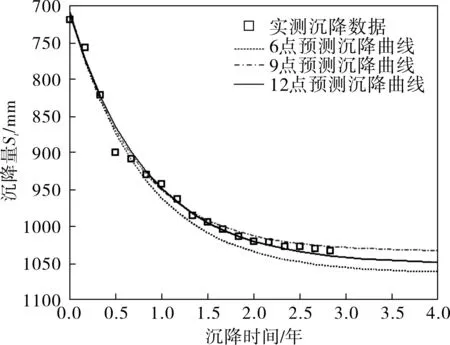
图2 6号沉降观测点实测数据与预测沉降曲线
由图 2看出,随着预测数据量的增加,预测曲线与实测沉降值也越接近,预测结果越精确。其中,采用6个实测数据点得到预测模型的最大误差为2.04%,而采用9个和12个实测数据点的最大误差仅为0.73%和0.67%。说明指数曲线法沉降预测模型得到的沉降增长曲线与地基实际沉降的变化规律相似,能够准确预测出在役储罐地基沉降随时间的变化值。
2 基于沉降预测模型的在役储罐疲劳寿命分析方法
2.1 基于实测地基沉降的弹性地基接触非线性有限元模型
大型储罐的环墙式基础主要由钢筋混凝土环梁和复合弹性砂土地基组成[12],混凝土环梁和复合弹性地基自身也是弹性体拥有不同的弹性模量。罐周测量点均布于外圈的混凝土环梁上。当储罐运行过程中罐周发生不均匀沉降时,实为罐周圈梁上各点产生了向下的沉降位移。因此针对在役储罐地基产生不均匀沉降的实际情况建立弹性地基接触模型,如图3所示。模型考虑了储罐底板与地基的水平摩擦力,把环梁和中间复合弹性地基视为拥有不同弹性模量的变形体。罐周的不均匀沉降值将通过离散傅里叶变换方法得到的不均匀沉降位移函数施加到环梁的上表面,以模拟地基产生不均匀沉降变形。

图3 沉降下的储罐地基接触模型
依据储罐地基的结构参数建立三维有限元模型进行非线性接触分析,其中,储罐大角焊缝(包含未焊透区域)周边区域和地基采用C3D8R实体单元,远离大角焊缝处的罐壁和底板采用S4R壳单元,储罐的固定顶采用刚性平面模拟,其总体与局部模型如图4所示。
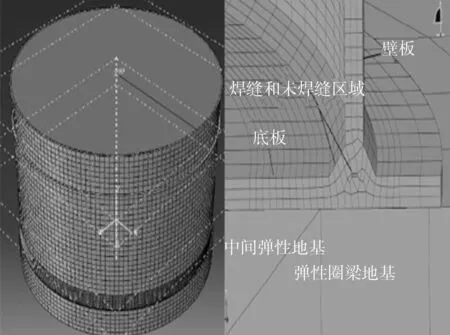
图4 储罐-地基接触有限元模型
储罐整体施加重力加速度g,储液的液柱静压力p施加在储罐的内表面,其大小为:
p=ρ1g(h1-y)
(6)
式中h1——储液的高度;
y——罐体的高度坐标。
由于储罐罐周沉降点的数据是离散的,不能直接作为沉降位移加载到圈梁地基上,需要将离散的沉降点变换为连续的傅里叶级数形式[5,13,14],笔者对实测沉降值采用离散傅里叶变换方法,将离散的沉降点通过有限傅里叶近似拟合成一个连续的三角函数:
(7)

对某实际案例中t=12时刻的罐周实测沉降数据进行离散傅里叶变换。其f(θ)沉降函数曲线与实测数据点对比如图5所示。

图5 沉降函数f(θ)与实测沉降数据效果对比
其中,f(θ)=12.6cos4θ-27.5cos2θ+2.75sin2θ-10.3cos3θ-0.141sin3θ-22.7cosθ+6.86sinθ+1170;加载到环梁上的不均匀沉降位移函数为12.6cos4θ-27.5cos2θ+2.75sin2θ-10.3cos3θ-0.141sin3θ。
采用API 653中判定系数R2≥0.9校核离散傅里叶变换方法的有效性[15]:
(8)
其中,Syy=∑(Sm-Smt)2,SSE=∑(Sm-Sf)2;Sm为实测沉降点的值;Smt为实测沉降点的均值;Sf为拟合函数曲线的值。
由本文拟合得到傅里叶函数f(θ)经过每个罐周的实测沉降点可知,Sm=Sf,SSE=0,故R2=1,已经达到R2的最大值。可认为本文中的离散傅里叶变换方法得到的f(θ)函数曲线是最为准确有效的罐周沉降数据曲线。
2.2 在役储罐不同沉降时刻下的疲劳寿命分析方法
采用指数曲线法对地基实测沉降数据进行预测,得到储罐服役中不同沉降时刻下的地基沉降预测值,建立储罐服役过程中的地基沉降-时间函数模型,作为后续疲劳分析的沉降边界条件。
结合储罐的结构参数和其地基沉降-时间函数模型,采用弹性地基接触有限元分析方法,对储罐在不同沉降时刻下的结构应力进行模拟分析,计算出不同沉降时刻下的峰值应力值SV,得到交变应力强度值Salt=0.5SV。按照JB 4732附录C 中图C1设计疲劳曲线,以及插值法计算在役储罐的许用循环次数N[16]:
(9)
其中,S、Si、Sj为交变应力幅值;Ni、Nj为设计疲劳数据中Si、Sj对应的循环次数。在役储罐的剩余循环次数N′计算式为:
N′=(T-t)a
(10)
其中,T为设计使用寿命;t表示已经服役时间;a表示单位时间内的周转次数。
将N和N′进行对比分析,当N≥N′时表明储罐服役期间不会由于不均匀沉降发生疲劳破坏,当N 某固定顶储罐容积为10 000m3,存储介质为对二甲苯,储罐罐壁和底板材料为Q345R钢板,内径φ28 500mm,罐壁高度17 818mm,最大储液高度17 030mm;边缘板厚度t1=12mm,宽度780mm;腐蚀裕量:底板2mm,罐壁1mm;设计寿命50年,年周转次数60次;各层壁板和地基几何参数列于表2,材料性能参数列于表3。 表2 罐壁和地基几何参数 表3 罐壁和地基材料性能参数 储罐地基经过充水预压处理后正式服役,其罐周地基环梁上均布的8个沉降测量点的实测沉降数据见表4。 表4 储罐罐周各沉降点实测沉降数据 由表4中所列储罐罐周各沉降点实测的现有的16个月的沉降数据,应用指数曲线法,预测储罐后期16月服役过程中的地基沉降值,预测结果见表5。 表5 储罐罐周各沉降点沉降预测值 对表4、5中的实测和预测沉降数据进行离散傅里叶变换,将得到并分离出连续的储罐罐周不均匀沉降函数加载到罐周地基上,建立弹性地基接触有限元模型对储罐结构进行分析,结果分别如图6、7所示,所得的疲劳循环寿命计算结果见表6。 图6 不同沉降时刻下储罐最大Mises 图7 不同沉降时刻下储罐底板与 服役时间月峰值应力MPa许用循环次数N剩余循环次数N'0451.71662830002565.5797729904592.5694629806579.7741129708541.49076296010534.69423295012603.26587294014663.24971293016707.04052292018781.32945291020804.42683290022817.72546289024826.12465288026832.02409287028835.82374286030840.02337285032853.02225284034864.321332830 由表6可知,储罐服役过程中随着地基不均匀沉降值的不断增大,储罐的峰值应力总体呈上升趋势,储罐的疲劳循环次数减小。后期服役过程中,t=20时,储罐的许用循环次数N已经开始小于其剩余循环次数N′,表明此时储罐的疲劳寿命小于其设计使用年限,在服役期间将发生疲劳破坏。此时为了保证在役储罐的安全,可以采取的措施有:降低储罐的年周转次数,使得储罐在使用年限内的剩余循环次数N′小于许用循环次数N;调整储罐液位高度以降低储罐的峰值应力;对储罐地基进行纠偏处理,减小不均匀沉降量,保证储罐运行过程中的安全。 4.1针对建造在软土地基上在役储罐地基沉降特点,构建符合其地基沉降规律的指数曲线法预测模型。使用实测沉降数据对预测模型进行验证表明,指数曲线法沉降预测模型可以准确预测软土地基上在役储罐不同时刻的沉降量。 4.2针对在役储罐发生罐周不均匀沉降的实际情况,建立了基于沉降预测模型的在役储罐疲劳寿命分析方法。该方法由弹性地基接触有限元分析模型和在役储罐疲劳寿命分析方法组成,能够对在役储罐发生不均匀沉降后的疲劳寿命进行准确地预测分析。 4.3对某储罐发生不均匀沉降后服役期内疲劳安全性进行了实例分析。结合储罐周转情况,分析评定了储罐服役过程中的结构疲劳寿命。 [1] 魏化中,张占武,丁克勤,等.大型储罐角焊缝焊趾表面裂纹应力强度因子数值计算[J].化工机械,2014,41(1):88~94. [2] 卫德强,俞接成,张富成,等.含硫原油储罐的腐蚀分析及防腐措施[J].化工机械,2017,44(1):1~5. [3] 傅强,陈志平,郑津洋.弹性地基上大型石油储罐的应力分析[J].化工机械,2002,29(4):210~213. [4] 赵阳,曹庆帅,谢新宇.大型钢储罐的沉降与结构性能的关系[J].工业建筑,2007,37(4):65~68. [5] 陈凌志,赵阳.不均匀沉降下的大型钢储罐结构[J].空间结构,2003,9(3):50~54. [6] Mousa E A,Ruiz C.Stresses in Cylindrical Tanks Due to Uneven Circumferential Settlement[J].Strain,1979,15(1):7~9. [7] 程香,陈志平,刘义君.基于基础沉降监测的在役大型油罐寿命预测技术[J].压力容器,2007,24(1):28~31. [8] 曾国熙,杨锡令.砂井地基沉陷分析[J].浙江大学学报(工学版),1959,(3):34~72. [9] 周鑫,张强,曾奕衡,等.指数曲线与双曲线拟合在软基沉降预测中的对比分析[J].探矿工程,2011,38(11):51~53. [10] 熊春宝,李法超.指数曲线模型预测基坑周边地面沉降[J].测绘与空间地理信息,2011, 34(4):4~6. [11] 徐至钧.油罐基础采用充水预压法加固软弱地基[J].建筑结构,1975,(3):11~25. [12] GB 50473-2008,钢制储罐地基基础设计规范[S].北京:中国计划出版社,2009. [13] Fan H G,Chen Z P,Shen J M,et al.Buckling of Steel Tanks under Measured Settlement Based on Poisson Curve Prediction Model[J].Thin-Walled Structures,2016,106:284~293. [14] Kamyab H,Palmer S C.Analysis of Displacements and Stresses in Oil Storage Tanks Caused by Differential Settlement[J].Journal of Mechanical Engineering Science,1989,203(13):61~70. [15] API 653-2009, Tank Inspection,Repair,Alteration and Reconstruction[S].Washington D C:American Petroleum Institute,2009. [16] JB 4732-1995,钢制压力容器-分析设计标准(2005年确认)[S].北京:新华出版社,2005.3 案例分析






4 结论
