基于小波分析的抗振动信号处理算法研究

熊婷婷

(安徽工业经济职业技术学院 电气工程学院，合肥 230051)

21世纪是一个科技大爆炸的年代，各个领域飞速发展.在很多领域的研究中，都需要对其系统所反馈回来的信号做分析，以此作为根据从而找到系统内部的相关故障[1].然而实际应用中，系统反馈回来的信号受到的影响较大，常常会带有较大的噪声，且故障信号是不稳定的，多是突变信号，这就大大增加了信号提取的难度[2].傅里叶分析在对突变信号检测时常因在时域不能局部化，导致检测到的突变信号不准确[3].

在检测突变信号时，常常用小波分析法，不仅能在时域局部化，同时还可以调节时窗和频窗的宽度[4].当获取一部分突变信号后，信号的函数图是一段连续的信号时，在信号的突变点处得到小波变换的模取极大值；当尺度增大时，多分辨小波分析中噪声所引起的模的极大值就会迅速减小，这样突变信号就得以被识别[5].小波分析被广泛应用，不仅因其能在低噪比的信号中提取出故障信号，还因其能在一定程度上滤去噪声.

1 抗振动降噪机理分析

1.1 小波去噪的概念

小波去噪是根据某一衡量准则去寻找最接近真实信号的信号值，最终目的是为了去除噪声，其本质是数学上的函数逼近问题.由于小波基函数的一系列函数变换会形成一个函数空间，把含噪信号映射到小波函数空间内，找到最佳映射结果，从而得到恢复后的真实信号，这就是小波去噪[6].

1.2 去噪模型构建

在信号提取过程中，设一个信号为f(n)，因噪声影响后为s(n)，基本情况有：

(1)对小波进行一维信号分解.在函数空间中选择一个小波，以层次m进行分解，再对被污染后的s(n)进行m层分解.

(2)为得到原始数据信号小波系数的估值，实验过程中要对小波系数做门限阈值处理，阈值处理可使用软、硬阈值处理，即可根据情况选择适合的阈值形式.

(3)对一维小波进行重构.在(1)中我们对小波进行一维m层的分解，根据m层的低频系数和高频系数(经过量化处理后的1到m层的系数)进行小波重构.

1.3 去噪方法与特点

在了解小波去噪方法前，首先介绍一下小波去噪的主要依据，当尺度不同时小波系数的信号和噪声会有不同的表现特征.函数空间内的函数是不连续的，其中大部分函数集中在小波空间内，且集中在一部分子集内.所有小波系数都受到的是贡献相同的噪声.噪声向量及它的正交变换都是高斯形式[7].

小波去噪方法的分类：(1)强制去噪.先将高频系数(小波分解结构中的高频系数)都设为0，即去除全部高频分量，再将去噪信号重构，此时的信号虽然容易丢失有效信号但信号曲线更平滑.(2)用默认阈值法去噪.利用ddcncmp函数，去产生默认阈值，再进行去噪处理.(3)给定阈值(软硬)再进行去噪.根据公式可在实验过程中获得阈值，相对于默认阈值，这种阈值可信度更高.

小波变换时有四大特点[8]，由于这些特点使得小波去噪得以成功进行.(1)低熵性：小波变换后使小波系数的熵降低.(2)小波变换具有多分辨率特性.当分辨率不同时，对不同分辨率下的噪声和信号进行去噪处理.(3)去相关性.对小波变换的信号可以去相关性，噪声在小波变换后会有白化趋势，综上时域没有小波域利于去噪.(4)可灵活选基.因为小波变换具有选基灵活的特性，所以试验中可以选择多种小波母函数.

2 理论分析

基于一簇函数的连续小波变换：

(1)

式中：设Ψ是一个在频域和时域上有限且固定的函数，且满足：

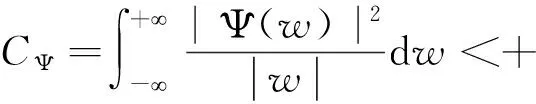
(2)

式中：CΨ为小波常数，Ψ为基小波，Ψ在变换后得到小波函数Ψ(a,b)(t)，其中a是伸缩因子，b是平移因子，定义信号f(t)经过变换后：

(3)

当函数f(t)满足以下条件时：

(4)

上式逆变换后，得：

(5)

在采集汽车上的震动信号s(t)时，一般情况下是由两部分信号组成，即真实信号和噪声信号，具体关系有：

s(t)=f(t)+σe(t)

(6)

式中：σ是指噪声强度.

当去除e(t)且恢复f(t)后，即可获得无噪声的是s(t).小波变换具有多分辨率性，所以在对目标信号和噪声信号进行处理时更易获得真实信号，对比传统方法，小波去噪更具优势.

图1 小波去噪工作机理示意图

综上概括小波去噪的原理为：应用小波变换的方法，把信号进行一维分解，再在不同尺度下去除噪声部分的小波系数，将剩余的小波系数进行增强处理，重构出的信号即为小波去噪后的信号.图1是小波去噪的原理图.

图1中，Fσ是阈值算子，当阈值算子起作用后，模值大的系数会被保留，模值小的系数会被置0，即：

(7)

式中：Cm,n是阈值作用前的小波系数数值，(FδC)m,n为阈值作用后的小波系数数值，δ是可置参数.Mask是掩值算子，它可以保留特定的系数，并将系数置为0.即：

(8)

式中：(Maskc)m,n为阈值作用后的小波系数数值，Q为允许系数条件.

由图1可知，采用小波去噪的过程为：

(1)对采集信号是s(t)进行n层一维分解，分解层次设为n.

(2)给不同层次的分解系数选择阈值，对不同层的系数进行相应的阈值处理.

(3)将分解后的小波系数进行重构，把噪声信号去除从而恢复原始信号.

(4)通过将重建后的信号再次提取从而将振动噪声消除，将新的数据重新保存.

3 实验

3.1 仿真分析与预处理

振动噪声是实际工程应用中最常见的噪声，正常信号多为低频信号，而含有噪声的信号多为高频信号，因为噪声大多不是平稳的白噪声，所以信号中常有尖峰或者突变等现象，如何去处理这些信号，就成了工程应用中最为紧要的任务.

在处理这部分信号时，一般先进行信号的预处理，传统方法多使用傅里叶变换，但对于这类包含高频信号的处理，傅里叶变换很难达到一个良好的处理效果，而小波分析法能对信号进行时域和频域的同时处理，且有自动变焦的功能，所以小波分析更适合处理含有高频信号的噪声，处理结果也更为精确.

3.2 算法设计

在本文中采用了子小波去噪技术，这种技术基于阈值(基于极大极小化思想所选取)处理的思想，以最大概率逼近为约束条件去约束处理后的信号和原始信号，采用软阈值，综上对子波系数做处理，从而提高信噪比，达到很好的去噪效果.

(9)

其中t为软限幅值函数的阈值.

用Matlab来实现Donoho的消噪处理.

软阈值决策算法核心有三步：

(1)采用db4小波对信号进行一定层数的小波分解.

(2)阈值根据式(2)选取，并对子波波系数做软阈值处理.

(3)选择被分解处理后的子波系数，用Mallat算法进行重构，重构后的信号即为消噪信号.

3.3 实验结果与讨论

本文用MATLAB对某震动信号进行仿真处理，以说明小波分析法在去噪时的有效性.输入信噪比为6.493 1 dB的信号，且小波基为sym6，设分解层数为5层，试验中噪声方差0.674 3，实验结果如图2所示.

(a)滤波前

(b)滤波后

从图2中不难看出，对仿真信号在三种阈值条件下去噪后，可以检测到信号的特征频率及信号发生的时间；在采用新阈值函数所得到的去噪信号比其他阈值函数的均方差要小的多.将实验数据列表如表1所示.

由于实验数据量较大，所以给出的是一个周期的特征点的数据值，但是整个周期中的数据都是具有一致性的.根据以上实验结果可得，当经过小波去噪后，数据误差明显降低了，平均误差优于2.5%，相比未处理的误差具有很大的改善.小波分析对于振动信号的处理有更好的效果，小波分析因其具有良好的时间分辨率等特性，在对时变和突变信号进行去噪处理上比传统去噪方法有更好的效果.由此可见，本算法在实现抗振噪声消除上具有较好的效果.

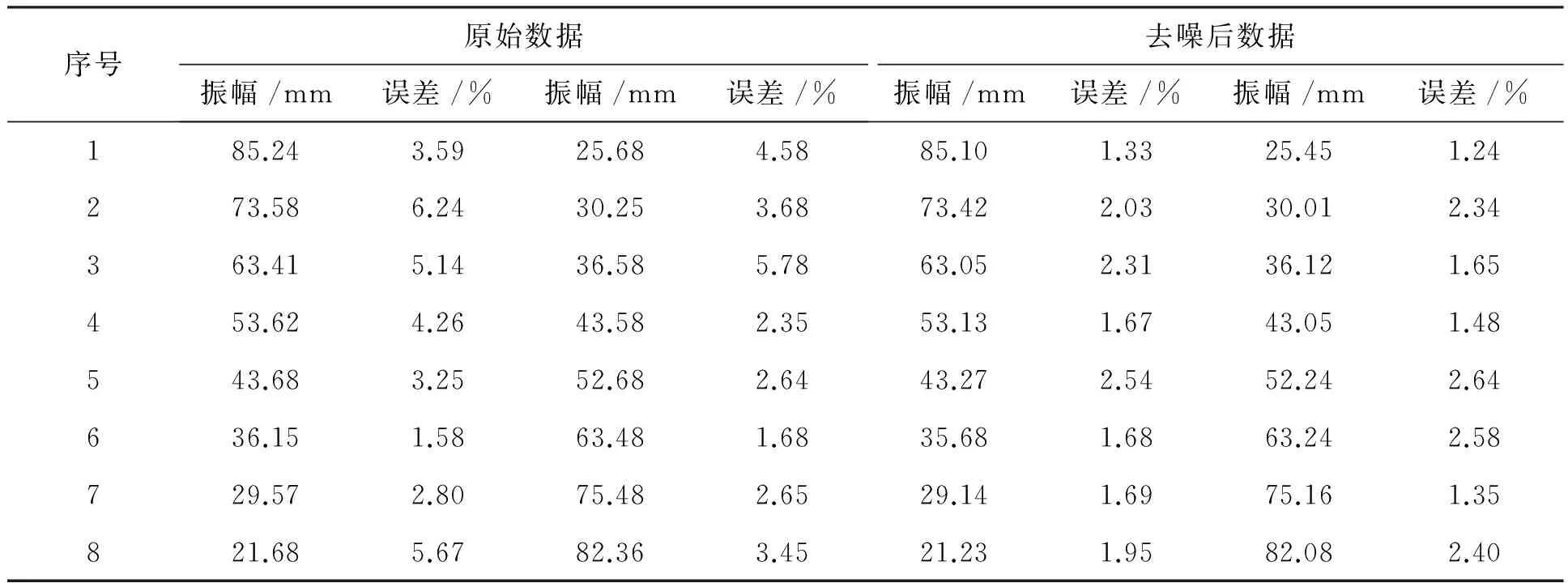
表1 实验数据对比

4 结论

本文研究了一种基于小波分析的信号分析处理算法，用于对振动引起的数据误差进行校正.在介绍了小波分析的基本原理的基础上，给出了小波去噪的特点和工作方法，计算推导了小波去噪对振动噪声抑制的函数形式.由对振动测试的实验数据可知，经小波去噪后的数据振幅相对降低，且总体差异不大，但其误差有了明显的改善.综上所述，本系统中的处理算法对由于振动产生的噪声的抑制效果明显，具有一定的实际应用价值.

[1] EEIKSSON P,FRIBERG O.Ride comfort optic cmizatioan of a city bus[J].Sturcturaul and Mulitidiashplinary Optimization,2000,20(1),67-75.

[2] 张鄂，刘中华，计志红，等.车系统的人体乘坐舒服性仿真及使用研究[J].工程设计学报，2010,17(2)：107-113.

[3] C Sidncy Burrus.小波与小波变换导论[M].程正兴译.北京：机械工业出版社，2008.

[4] 崔华，宋国乡.基于小波阈值去噪方法的一种改进方法[J].现代电子技术，2005，28(1) ：8-9.

[5] 夏均忠，马宗坡，方中雁，等，汽车平顺性评价方法综述[J].噪声与振动控制，2012(4)：1-2.

[6] ISO 2631-1-1997 Mechannial vicbration and shock-evauluation of human expose to whole-body vibration-part 1.general requirements[S].Beijing;Internamational Organnization for Standardization,1997：1-6.

[7] KAREN Y,KAYA N，OZTORK F,et al.A desigan tool to evaluate the vehicle ride comfort characteeistics；modeling,physical testing,and analysis[J].The Intermational Journal of Advanced Manufaacturning Techehonlogy，2012，60(5-8)：755-763.

[8] JAZAR R N.Asvanced vibration[M].New York：Springer US，2013：591-666.