颗粒粒径对回转窑内散体物料休止角的影响规律

刘义伦，王燕鹏，赵先琼



颗粒粒径对回转窑内散体物料休止角的影响规律

刘义伦1, 2，王燕鹏1，赵先琼1

(1. 中南大学 机电工程学院，湖南 长沙， 410083；2. 中南大学轻合金研究院，湖南 长沙， 410083)

为了研究颗粒粒径与回转窑内散体物料休止角的关系，建立回转窑物料运动实验平台。以直径为2~10 mm的玻璃珠为物料样本，测试不同粒径的物料在回转窑中的运动过程。通过数字图像处理法计算物料休止角随时间的响应过程，分析不同粒径条件下散体物料休止角的变化规律。研究结果表明：在回转窑中，无论是单一粒径物料还是多粒径组合物料，休止角的最大值、最小值、均值、极差和周期都会随着颗粒粒径的增大而增大；在多粒径组合物料中，“巴西果效应”使不同粒径的颗粒出现分离，粒径偏大的颗粒运动到物料的外围区域，使得物料休止角的最大值、最小值、均值、极差和周期都增大；在平均粒径相同的多粒径组合物料中，颗粒间的粒径差值越大，休止角的最大值、最小值、均值、极差和周期越大。

回转窑；颗粒物料；粒径；休止角

回转窑是一种广泛应用于能源、化工、冶金等行业中的工程设备，主要用于散体颗粒物料的运输、混合、烧结等过程处理。休止角是回转窑中散体颗粒物料自由界面与水平面之间的夹角[1−2]，也称为安息角，可以表征物料在回转窑中的运动状态，用于监测和控制物料的热工过程[3]，是研究回转窑内传质传热过程的重要特征参数[4−9]。对物料休止角的研究有助于进一步分析和掌握回转窑内传质传热过程。休止角作为反映物料属性的重要参数[10]，其值受物料颗粒间密实度、物料黏度、物料的含水率、表面粗糙度的影 响[11−14]。然而，人们对关于颗粒粒径对物料休止角的影响规律的研究较少。在针对玻璃珠[12−13]、沙粒[11, 15]、铁珠[16]等单一粒径分布颗粒材料的研究中，一些研究者通过漏斗堆积法获得颗粒材料的休止角，认为粒径并不是影响散体物料休止角的直接因素，而是通过颗粒形状、粗糙度等因素来间接影响休止角；一些研究者通过回转窑转动法获得颗粒材料的休止角[1, 17−18]，经测试分析后认为，影响休止角的主要因素是颗粒粒径与回转窑窑直径的比值，而物料填充率和回转窑转速几乎不改变休止角。以上研究虽有涉及回转窑中粒径对休止角的影响，但是，所用颗粒物料的粒径均为单一粒径分布，没有涉及多粒径组合的颗粒物料。而在实际回转窑中，使用的物料一般具有多粒径组合状态的特征，因此，有必要针对这一特征对颗粒物料的休止角进行进一步研究。为此，本文作者通过搭建回转窑物料运动试验平台，以玻璃珠为颗粒样本，测试颗粒物料在回转窑中的运动过程；通过数字图像处理技术对休止角进行计算，从多角度研究粒径与休止角的关系，以探明颗粒粒径对散体物料休止角的影响规律，为控制和优化回转窑内传质传热过程提供参考。

1 实验

1.1 实验设备与材料

回转窑物料运动试验台主要由玻璃钢转筒、带控制器的电动机和减速器构成，转筒在电机的驱动作用下绕其中心轴旋转，通过电动机调速器可对回转滚筒进行0~20 r/min调转速。转筒内物料运动区域长度为50 mm，内径为280 mm，转筒一端封闭，另一端在装料后使用透明玻璃板封闭。由于在实际工业生产中，入窑前的生料经过破碎后的粒径分布为1~12 mm，故本实验选用粒径为2，4，5，8和10 mm的圆球形玻璃珠模拟不同粒径的颗粒物料在回转窑中的运动 过程。

1.2 实验方案

本实验分别对6种不同粒径的玻璃球材质散体物料进行同等条件下的多次单一粒径实验和多粒径组合实验。在实验过程中，试验台水平放置。为方便观察实验并准确提取摄像数据，筒体转速均设置为 1 r/min，物料填充率均为16%。

2 物料休止角的计算

物料的休止角采用数字图像处理法[19]进行计算，具体过程如图1所示。通过Adobe Premiere Pro CS4软件将摄像所得录像解帧为图像序列(5帧/s)；使用Mat lab软件对图像进行滤波、分割等技术处理；在此基础上提取物料的自由界面边缘线，并采用最小二乘直线拟合方法对所提取边缘线进行直线拟合；拟合所得直线倾角即为图像所对应瞬时散体物料的休止角。由于录像通过解帧后所得到的图像序列与相应的时间序列一一对应，故对该图像序列进行批量处理，即可得到某连续时间段内物料休止角随时间的响应过程。

(a) 截取图像物料部分；(b) 提取物料边缘线；(c) 直线拟合边缘线

以直径为8 mm的玻璃珠物料为例，图2(a)所示为采用数字图像处理法计算的物料休止角随时间的响应过程，图2(b)所示为回转窑内物料运动状态示意图。从图2可以看出：当试验台开始工作后，物料休止角由初始值(接近为0°)逐渐增大，在静摩擦力作用下物料随转筒一起转动，两者之间没有发生相对运动；当物料被转筒带到一定高度时(此过程休止角变化情况对应图2(a)中段)，静摩擦力以及离心力不足以克服重力的影响，靠近转筒中心的表层物料开始往下滑动，休止角开始减少；当休止角减少到一定程度后，物料处于最低势能位置，休止角不再减少，物料开始进入一个随转筒运动而上升的状态(休止角变化情况对应图中的段)；当休止角上升达到某一值后又开始下滑，如此往复。物料在转筒内的运动过程是一个上升、下滑、再上升的动态过程，休止角呈现出围绕均值上下波动的周期性变化规律，如图2(a)中的→→→→→等即构成1个完整的运动周期。由于实验并不是在理想条件下进行的，故此图像中的周期性规律并不完全符合数学意义上的理想周期，每个周期、波峰波谷并不完全相同，如图2(a)中的极值点，，和点所对应的休止角也并没有达到该周期内应有的最大值或最小值，该系列点属于“伪极值点”；而→→，→→，→→等也并不能算作完整的周期，与整个运动过程相比，属于“伪周期”；若忽略伪周期的影响，则在物料完成1次上升和下滑的过程中，休止角随时间变化的规律如下：当休止角达到本周期内的最大休止角m后，迅速减小到本周期的最小休止角r，然后又从最小休止角开始不断增大，达到最大休止角时又开始新一轮上升下滑过程。休止角随时间变化范围为m＜≤r，两相邻波峰或波谷所对应时间差即为1个周期。

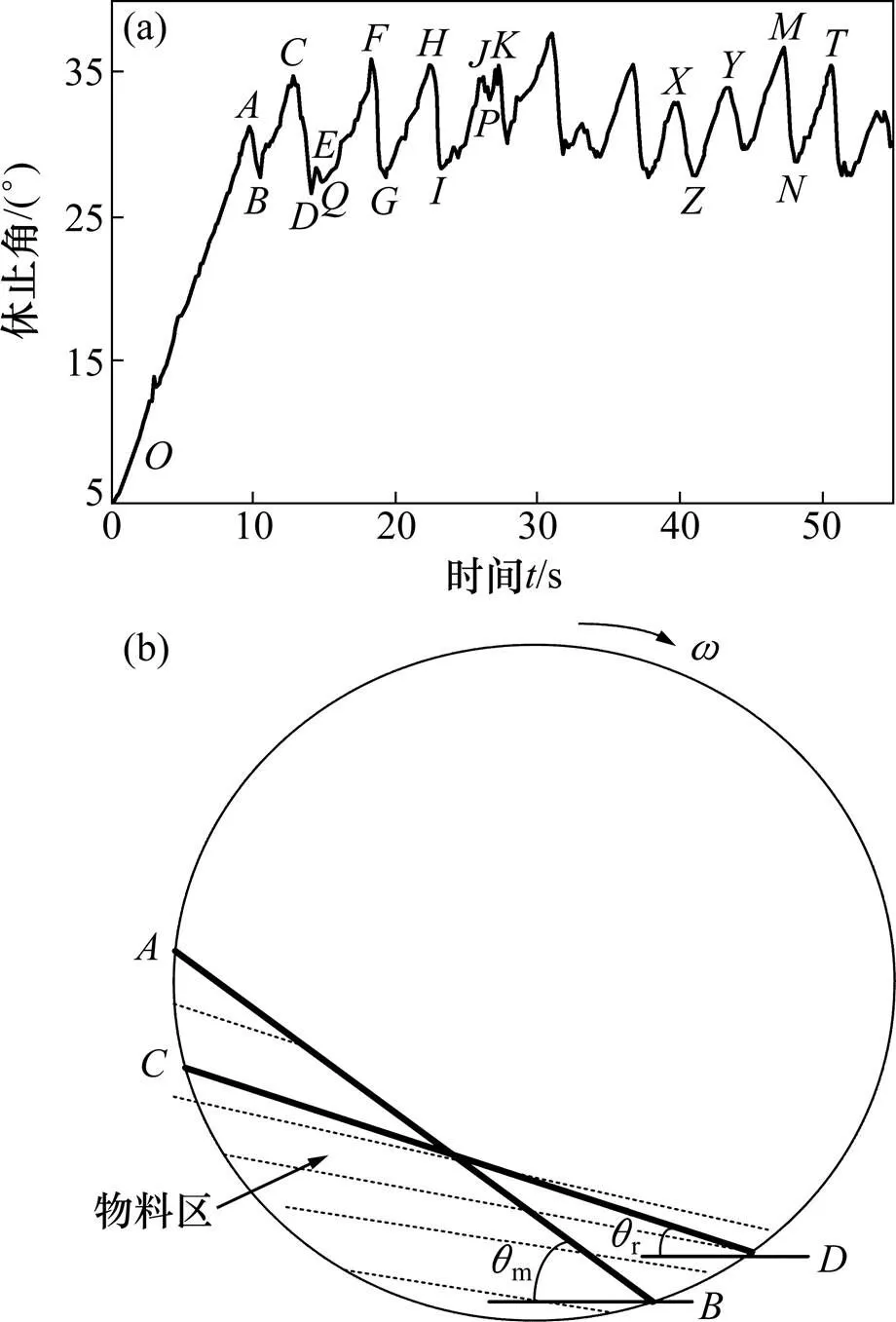
(a) 休止角随时间变化趋势；(b) 物料运动状态示意图

3 结果与讨论

3.1 单一粒径物料休止角

为研究单一粒径变化对散体物料休止角的影响规律，取直径分别为2 mm和4 mm等粒径的玻璃珠散体物料进行实验，得到它们各自休止角与时间的变化关系。经过对比分析发现：不同粒径的单一粒径物料休止角与时间的变化关系的整体趋势基本相同，即随着回转滚筒旋转，物料休止角呈现出围绕均值上下波动的周期性变化规律。为进一步比较分析各不同粒径的休止角差异规律，从各不同粒径的单一粒径物料休止角与时间的变化关系图中选取休止角周期性变化规律稳定的10个周期，计算各周期内的最大休止角、最小休止角、周期长以及休止角平均值，并求出最大休止角与最小休止角的差值(即极差)，如表1所示。

从表1可知：当实验物料粒径不同时，物料休止角的最大角、最小角、极差、均值和周期这5个参数都随着粒径的增大而呈现出增大的趋势。为进一步研究这5个参数与粒径的关系，据表1绘出这5个参数与粒径的变化曲线，如图3所示。

从图3可见：单一粒径物料休止角的均值、最值、极差与粒径都具有良好的线性相关性；在其他条件不变条件下，随粒径的增大，休止角的最大值、最小值、均值和极差均呈现增大的趋势。采用最小二乘法拟合其与粒径的数据关系，所得函数均为一次函数关系。

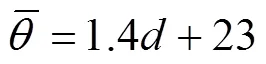
休止角极差c与粒径的关系为

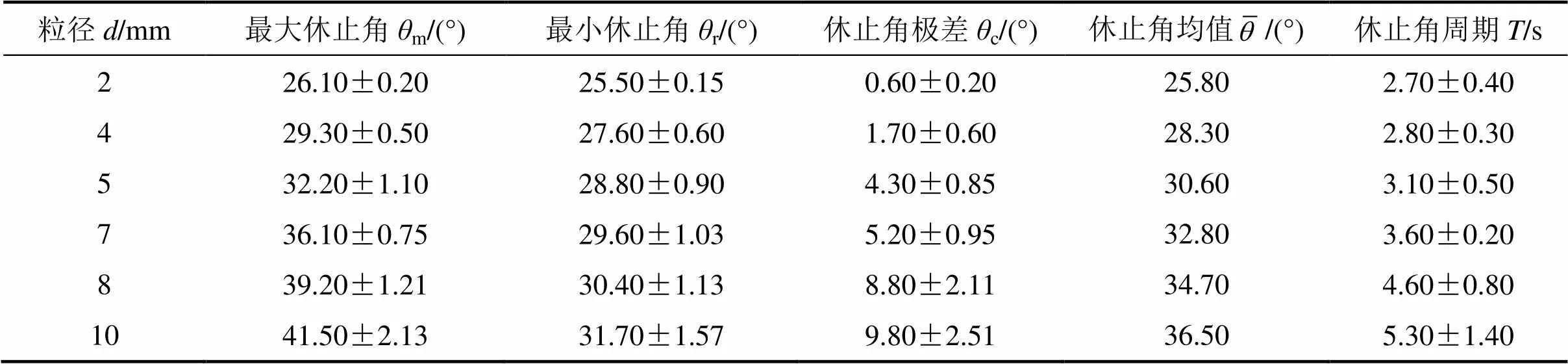
表1 单一粒径物料休止角相关参数与粒径的关系

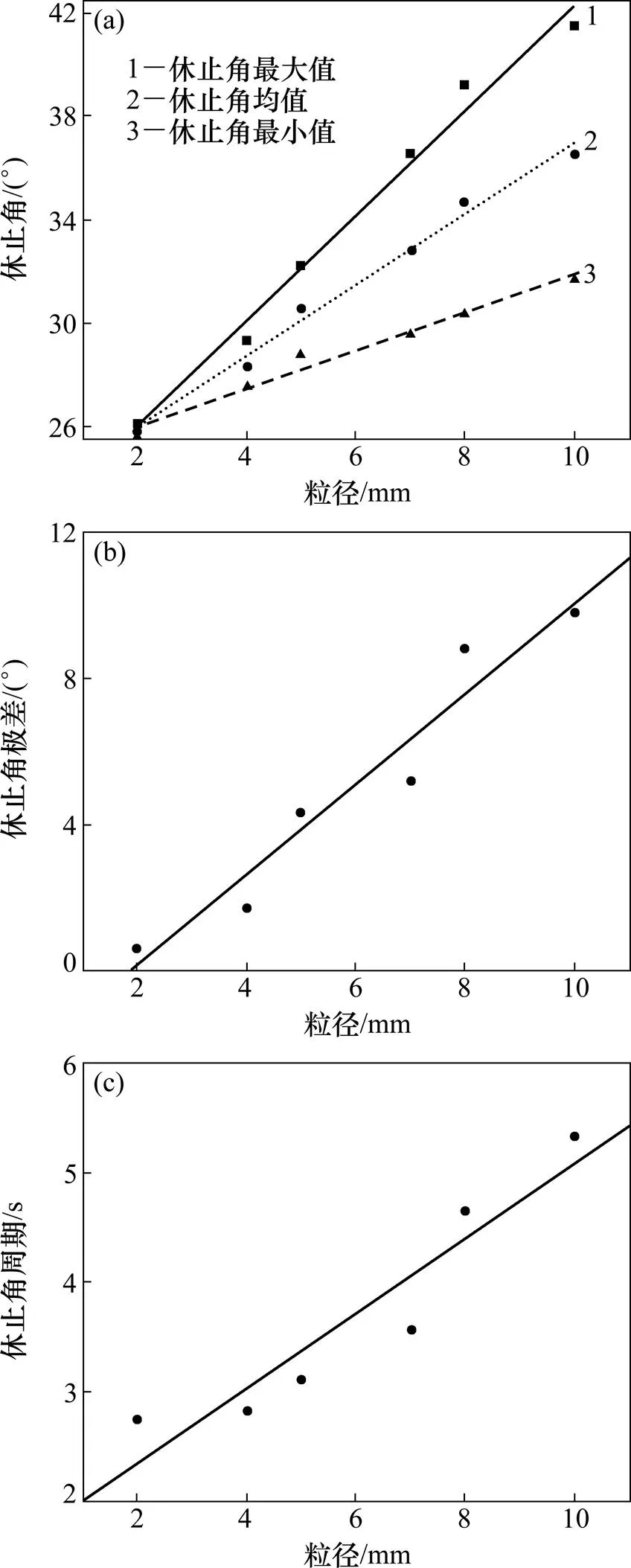
(a) 休止角；(b)休止角极差；(c) 休止角周期

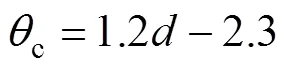
最小休止角r与粒径的关系为

最大休止角m与粒径的关系为

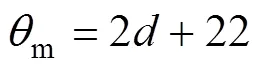
这是因为散体物料颗粒粒径越小，颗粒的流动性越好，颗粒之间越不容易堆积，所形成的物料休止角就越小；而较大的颗粒间虽然总接触点数较少，但由于物料颗粒球并不完全规则和光滑，所以，当粒径较大时，接触面也会相应变大，摩擦阻力变大，颗粒间的咬合力作用加强，故大粒径物料的休止角也较大。

从图3(c)可见：在回转滚筒尺寸、转速等其他条件不变的条件下，散体物料颗粒粒径不同，休止角周期也不相同，且粒径越大，休止角周期也越大。休止角周期与粒径的拟合函数关系式为

=0.34+1.6 (5)

观察各粒径休止角随时间变化规律发现：各粒径休止角从最大角变化到最小角所用的时间均在1.0~1.3 s以内，且并不随粒径增大呈现明显增大或减少的规律性趋势，而各粒径周期却从(2.7±0.4) s增大到(5.3±1.4) s，这说明从最小休止角变化到最大休止角占据整个周期的绝大部分时间，这与实际观察运动结果一致。故大粒径运动周期与小粒径运动周期相比较长，其原因主要是增大了从最小休止角变化到最大休止角的运动时间，而这段运动时间是物料随滚筒壁运动而被带着上升的过程，这说明影响不同粒径休止角变化的因素主要作用于物料随转筒运动上升的过程。

3.2 多粒径组合物料休止角

在实际生产过程中，生料在入窑前一般要先经过破碎、细磨、均化等工艺过程处理，以提高生料的分解率和回转窑的产量[21]，故深入研究多粒径组合物料中粒径对休止角的影响规律具有重要的实际应用 价值。

3.2.1 不同平均粒径物料休止角

为研究颗粒平均粒径对多粒径组合物料休止角的影响规律，选取5组不同平均粒径的多粒径组合物料分别进行实验，如表2所示。多粒径组合物料中组分量体积比约为1:1，实验前将物料混合均匀，按前面所述的单一粒径物料休止角实验方法进行实验，并以同样方法将实验结果处理成休止角随时间变化曲线，然后绘制休止角的这5个参数与粒径的变化曲线，如图4所示。

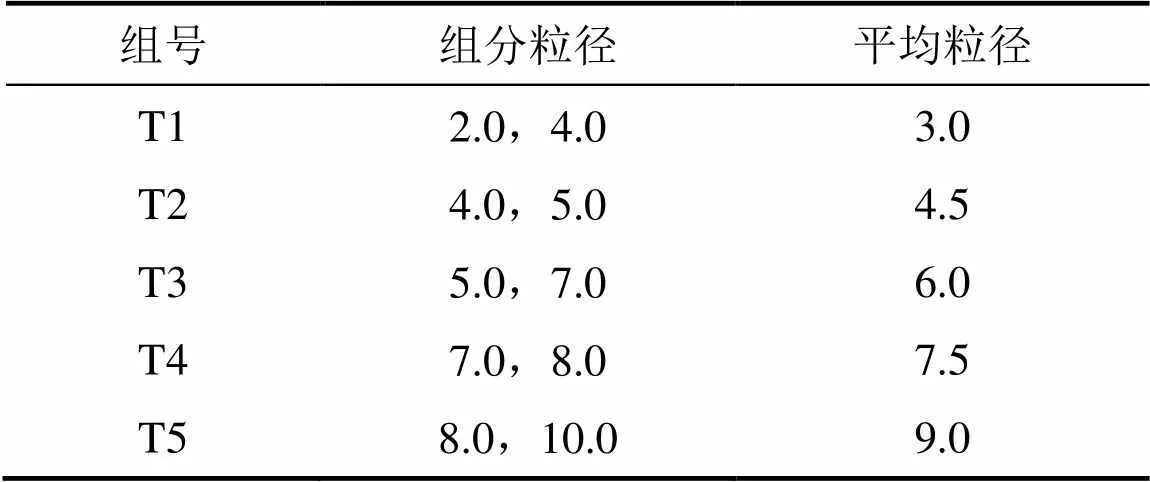
表2 不同平均粒径的物料

从图4可见：在其他条件不变的条件下，随着粒径改变，不同平均粒径物料休止角的最大角、最小角、极差、均值和周期等5个物理量都会发生变化，且均呈现出随颗粒平均粒径的增大而增大的趋势。这与单一粒径物料休止角变化规律相似。在本实验的多粒径组合物料中，平均粒径大的物料，其颗粒的粒径也较大，颗粒间的咬合力也会相应增大，颗粒间越容易堆积，使得物料休止角也越大。

3.2.2 相同平均粒径的物料休止角

为研究多粒径组合物料中组分间粒径差值对物料休止角的影响规律，取3组粒径均值同为6 mm但粒径差值不同的多粒径组合物料分别进行实验，所选实验物料粒径差值如表3所示。图5所示为具有相同平均粒径的3组多粒径组合物料休止角与粒径差值的响应关系。从图5可以看出：多粒径组合物料的5种休止角物理量均呈现出随多粒径组合物料中的组分间粒径差值增大而增大的规律。

回转窑的旋转会使处于混合状态的多粒径组合物料逐渐出现不同粒径颗粒径向分离的现象，这种现象被称为“巴西果效应”[22]，分离后的小颗粒主要聚集在物料中心区域位置，而大颗粒则逐渐扩散到物料的外围区域，对小颗粒呈现环绕包围的状态。从整体看，大颗粒还要受到小颗粒的支撑作用，而小颗粒则受到大颗粒的隐蔽影响，使得散体物料休止坡面稳定性增强[15]，从而使物料的休止角偏大。因此，多粒径组合物料中不同粒径颗粒的径向分离，会使多粒径组合物料休止角的最大值、最小值、均值、极差和周期均变大。

(a) 休止角；(b) 休止角极差；(c) 休止角周期

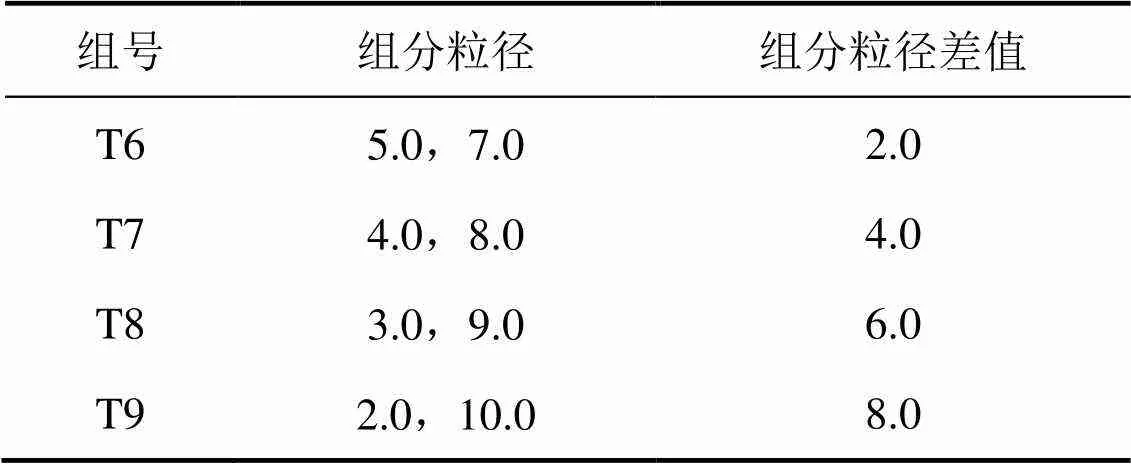
表3 物料粒径

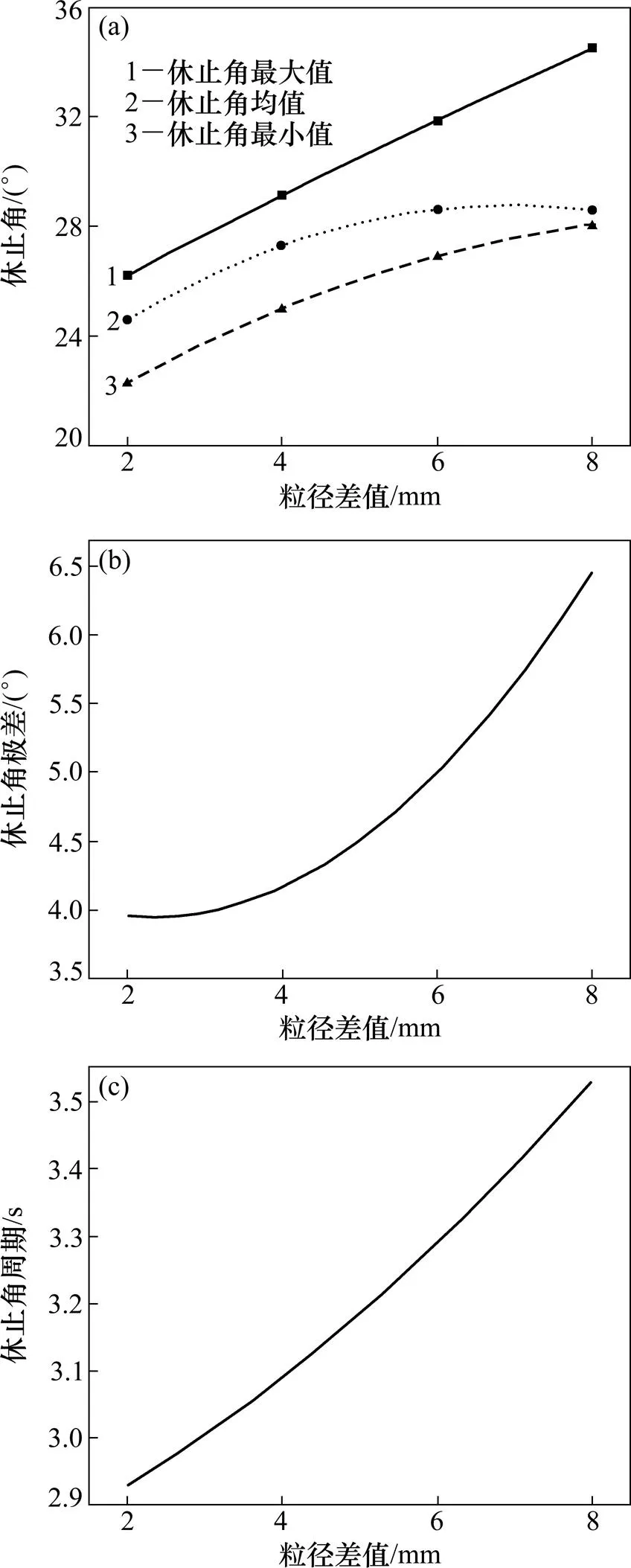
(a) 休止角；(b) 休止角极差；(c) 休止角周期

颗粒粒径为4 mm和8 mm组合的散体物料休止角随时间变化规律见图6。从图6可以看出：休止角从=10 s开始呈现出相对稳定的周期性规律，但= 20 s后(对应图中的段)的休止角周期性规律与=20 s前(对应图中的段)的休止角周期性规律存在较大的差异；段的物料休止角的最大值、最小值、均值、极差和周期均明显比段的大。观察实验物料在转筒中的实际运动可发现：在=20 s之前，粒径分别为4 mm和8 mm的玻璃球还处于不断变化的混合状态，尚未出现明显的径向分离现象，但粒径相同的颗粒之间开始出现聚集趋势；在=20 s后，不同粒径的颗粒间径向分离现象较明显，粒径为4 mm的小颗粒大部分已运动到物料中心区域位置，而粒径为8 mm的大颗粒则明显扩散到物料的外围区域，主要分布在贴近转筒的稳定层和靠近转筒中心的物料自由界面层，呈现环绕包围小颗粒的状态。当多粒径组合物料中大、小颗粒粒径差值越大时，大、小颗粒径向分离速度也越快，出现大、小颗粒径向分离的“巴西果效应”现象也越明显[23]。由于3组实验物料的粒径均值相同，故对于粒径差值大的多粒径组合物料，其大颗粒粒径更大，大、小颗粒径向分离后休止角增大的效果也会更明显，因而使得粒径差值较大的多粒径组合物料的休止角等5个物理量均会比粒径差值较小的多粒径组合物料的大。

图6 周期性规律变化示例图

4 结论

1)随着回转窑的旋转运动，窑内物料休止角呈现出围绕均值上下波动的周期性变化规律，且休止角周期随粒径增大而增大。

2)颗粒粒径对回转窑内散体物料休止角有较大的影响。随着粒径增大，用来衡量单一粒径物料休止角最大角、最小角、极差、均值和周期均呈现出增大的趋势，且均与粒径呈线性正相关。

3)多粒径组合物料休止角的最大角、最小角、极差、均值和周期均随物料平均粒径的增大而增大。

4)“巴西果效应”会使混合状态的多粒径组合物料中的不同粒径的颗粒之间发生径向分离，出现小颗粒聚集在物料中心区域位置，大颗粒则逐渐扩散到物料的外围区域，对小颗粒呈现环绕包围的状态，导致多粒径组合物料休止角的最大角、最小角、极差、均值和周期均变大；当平均粒径相同时，多粒径组合物料各组分间的粒径差值越大，物料休止角的最大角、最小角、极差、均值和周期也越大。

[1] LIU Xiaoyan, SPECHT E, MELLMANN J. Experimental study of the lower and upper angles of repose of granular materials in rotating drums[J]. Powder Technology, 2005, 154(2): 125−131.

[2] CHEN Hui, LIU Yilun, ZHAO Xianqiong, et al. Numerical investigation on angle of repose and force network from granular pile in variable gravitational environments[J]. Powder Technology, 2015, 283: 607−617.

[3] LIU Xiaoyan, ZHANG Yaoyao. Real-time detection of the repose angle of solids in rotating drum based on image processing[C]//Advanced Measurement and Test (AMT 2011 Part 2). Nanchang, China: Advanced Materials Research, 2011: 748−751.

[4] CHEN Hui, ZHAO Xianqiong, XIAO Yougang, et al. Radial mixing and segregation of granular bed bi-dispersed both in particle size and density within horizontal rotating drum[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(2): 527−535.

[5] 王春华, 陈文仲, 梁增英, 等. 炭素回转窑内物料运动形式的确定[J]. 工业炉, 2008, 30(4): 34−36. WANG Chunhua, CHEN Wenzhong, LIANG Zengying, et al. Determination of solid particles motion types in rotary kilns[J]. Industrial Furnace, 2008, 30(4): 34−36.

[6] 刘刚, 池涌, 蒋旭光, 等. 颗粒物料在回转窑内的运动特性模型[J]. 浙江大学学报(工学版), 2007, 41(7): 1195−1200.LIU Gang, CHI Yong, JIANG Xuguang, et al. Model of axial transport of particles in rotary kiln[J]. Journal of Zhejiang University (Engineering Science), 2007, 41(7): 1195−1200.

[7] 曲航, 赵军, 刘晓燕. 回转窑内滚动状态下颗粒横向运动的影响因素的实验研究[J]. 硅酸盐通报, 2007, 26(3): 441−446. QU Hang, ZHAO Jun, LIU Xiaoyan. Experimental study on the influence factors of transverse motion of particle at rolling regime in the rotary kiln[J]. Bulletin of the Chinese Ceramic Society, 2007, 26(3): 441−446.

[8] WANG Junjie, ZHAO Di, LIANG Yue, et al. Angle of repose of landslide debris deposits induced by 2008 Sichuan earthquake[J]. Engineering Geology, 2013, 1565(2): 103−110.

[9] WONG A C Y. Characterization of the flow ability of glass beads by bulk densities ratio[J]. Chemical Engineering Science, 2000, 55(18): 3855−3859.

[10] FROEHLICH D C. Mass angle of repose of open-graded rock riprap[J].Journal of Irrigation & Drainage Engineering, 2011, 137(7): 454−461.

[11] 刘建宝, 王乃昂, 程弘毅, 等. 沙丘沙休止角影响因素实验研究[J]. 中国沙漠, 2010, 30(4): 758−762. LIU Jianbao, WANG Naiang, CHENG Hongyi, et al. Influencing factors of repose angle of sand dunes: an experiment[J]. Journal of Desert Research, 2010, 30(4): 758−762.

[12] LI Yanjie, XU Yong, THORNTON C. A comparison of discrete element simulations and experiments for ‘standpipes’ composed of spherical particles[J]. Powder Technology, 2005, 160(3): 219−228.

[13] YANG Fengguang, LIU Xingnian, YANG Kejun, et al. Study on the angle of repose of non-uniform sediment[J]. Journal of Hydrodynamics, 2009, 21(5): 685−691.

[14] TEGZES P, VICSEK T, SCHIFFER P. Avalanche dynamics in wet granular materials[J]. Physical Review Letters, 2002, 89(9): 094301−094301.

[15] 王爱玲, 叶明生, 邓秋香. MATLAB R2007图像处理技术与应用[M]. 北京: 电子工业出版社, 2008: 97−118. WANG Ailing, YE Mingsheng, DENG Qiuxiang. MATLAB R2007 image processing technology and application[M]. 1st ed. Beijing: Electronics Industry Press, 2008: 97−118.

[16] 刘小燕, 周生健, 张小刚. 基于图像处理的回转窑物料休止角检测方法[J]. 控制工程, 2009, 16(4): 498−501. LIU Xiaoyan, ZHOU Shengjian, ZHANG Xiaogang. Measurement of repose angle of solids in rotary kilns based on image processing[J]. Control Engineering of China, 2009, 16(4): 498−501.

[17] 赵洁. 水泥回转窑系统的建模与控制研究[D]. 郑州: 郑州大学电气工程学院, 2014: 16−19. ZHAO Jie. The research of modeling and control of cement rotary kiln system[D]. Zhenzhou: Zhenzhou University. College of Electrical Engineering, 2014: 16−19.

[18] 陆坤权, 刘寄星. 颗粒物质[J]. 物理, 2004, 33(9): 713−721. LU Kunquan, LIU Jixing. Particle matter[J]. Physics, 2004, 33(9): 713−721.

[19] HONG D C, QUINN P V. Reverse Brazil nut problem: competition between percolation and condensation[J]. Physical Review Letters, 2001, 86(15): 3423−3426.

(编辑 陈灿华)

Influence of particle size on repose angle of bulk materials in rotary kiln

LIU Yilun1, 2, WANG Yanpeng1, ZHAO Xianqiong1

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China; 2. Light Alloy Research Institute, Central South University, Changsha 410083, China)

An experimental rotating kiln was developed to investigate the relationship between particle size and the repose angle of bulk materials in rotary kiln. Taking glass beads with diameters from 2 mm to 10 mm as samples, the flowability performance of granular materials within the rotating kiln was measured. The evolution of the repose angle with time was obtained through the digital image processing method, and then the effect of the particle size on the repose angle was analyzed. The results show that for either mono-dispersed granular materials or granular materials with various particle sizes, the maximum value, the minimum value, average value, range and cycle of the repose angle increase with the increase of particle size. “Brazil nut effect” causes separation among granular materials with various particle sizes, the larger particles will move to the peripheral area of the material bed, which makes the maximum value, the minimum value, average value, range and cycle of the repose angle increase. For the multi-particle composite materials with the same average particle size, the maximum, the minimum value, average value, range and cycle of the repose angle increase with the increase of the difference between particle sizes.

rotary kiln; granule; particle size; repose angle

10.11817/j.issn.1672−7207.2017.12.016

TP391

A

1672−7207(2017)12−3256−07

2016−12−03；

2017−01−28

国家自然科学基金资助项目(51374241)(Project(51374241) supported by the National Natural Science Foundation of China)

刘义伦，博士，教授，从事散体颗粒物质的传热传质机理研究；E-mail：liuyiluncsu@sina.com