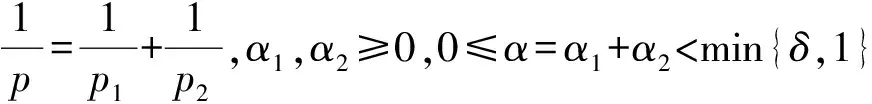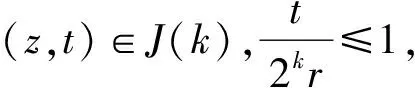具有非卷积型核的多线性Littlewood-Paley算子在Campanato空间上的新估计

周 疆,周 盼

(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830046)

众所周知,Littlewood-Paley算子(g-函数,面积积分S和g*λ-函数)在调和分析和偏微分方程中扮演着重要角色.g-函数和g*λ-函数是Littlewood和Paley[1]在研究Fourier级数时引进的,面积积分S是Lusin[2]在研究解析函数的边界值时引入的.自从20世纪70年代Coifman和Meyer[3]首次研究多线性奇异积分算子理论以来,多线性理论引起了Grafakos和Torres[4-5]的浓厚兴趣.关于具有非卷积型核的多线性Littlewood-Paley算子的研究已有很多,见文献[6-8]等.近来，许多学者对具有非卷积型核的多线性Littlewood-Paley算子也进行了研究,得到了一些结果.例如,2012年,Hart[9]研究了具有非卷积型核的面积积分S在Lebesgue和Sobolev乘积空间上的有界性，2014年,Shi等[10]得到了具有非卷积核的Littlewood-Paley算子在加权Lebesgue空间上的估计.

Littlewood-Paley算子在BMO和Campanato空间上的有界性研究可见文献[11-13].胡国恩等[14]得到了Marcinkiewicz算子在BMO和Campanato空间上的有界性；贺莎等[15]将Littlewood-Paley算子在文献[11-12]中的结果推广到了多线性情形,证明了具有非卷积型核的多线性Littlewood-Paleyg-函数、多线性面积积分S、多线性Littlewood-Paleyg*λ-函数在Campanato空间上的有界性.

1 相关定义及主要结果

Campanato空间是Campanato在1963年首次引进的,其定义如下.

定义1[16]设-n/p≤α<1,1≤p<∞,f是Rn上的一个局部可积函数,如果存在常数C1>0使得对于任意的球B⊂Rn,有

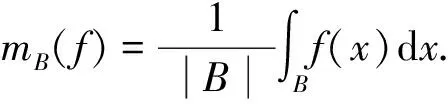
定义2设-n/p≤α<1,1≤p<∞,f是Rn上的一个局部可积函数,如果存在常数C2>0，使得对于任意的球B⊂Rn,有

定义3[15]设K(x,y1,…,ym)为定义在(Rn)m+1{(x,y1,…,ym):x=y1=…=ym}上的函数,如果对所有的(y1,…,ym)∈(Rn)m,存在常数C>0,使得K(x,y1,…,ym)满足以下条件:

本文的主要结果如下：

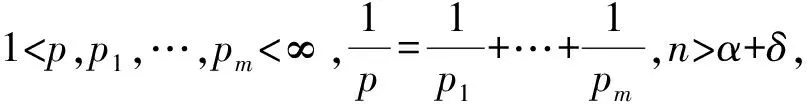
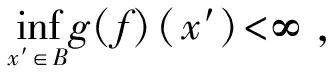
因此

通过以上不等式和定理1,容易得到以下推论.

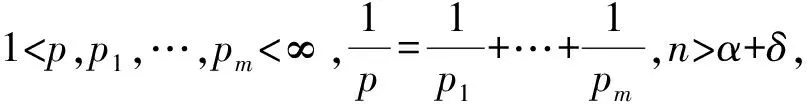
注记1文献[18]证明了在点态意义下S(f)(x)≤Cg*λ(f)成立,因此以上结果对于多线性Lusin面积积分S也成立.

2 主要结果的证明

首先证明定理1,仅考虑双线性的情形,对于m≥3情形类似可得.下面给出双线性Littlewood-Paleyg-函数在Lebesgue空间上的结果以及相关引理.

||g(f1,f2)||Lp(Rn)≤C||f1||Lp1(Rn)||f2||Lp2(Rn), ||S(f1,f2)||Lp(Rn)≤C||f1||Lp1(Rn)||f2||Lp2(Rn).

引理2[20]设f∈εα,p(Rn),1≤p<∞.如果β>0,-∞<α

其中C是仅依赖于n,α,β的常数.

定理1的证明只需证明对于任意fi∈εαi,pi(Rn),i=1,2,如果存在x0∈Rn使得g(f1,f2)(x0)<∞,那么对于任意的球B⊂Rn及x0∈B，有

不失一般性,假设||f1||εα1,p1(Rn)=1,||f2||εα2,p2(Rn)=1,B=B(xB,r)表示以xB为球心、以r为半径的球.对于任意的x∈B,设

则由核K的消失性条件(1)可得

首先估计I1,由引理1可得

现在估计I2,I3,I4.由对称性和引理3可知

g0((f1-m4B(f1))χ(4B)c,(f2-m4B(f2))χ4B)(x)≤C|B|α/n，

因此

I2≤C|B|2α/n，I3≤C|B|2α/n，I4≤C|B|2α/n.

最后,为了估计I5,仅需证明对于任意的x,x′∈B,有

|[g∞(f1,f2)(x)]2-[g∞(f1,f2)(x′)]2|≤C|B|2α/n.

由于

对于任意的t≥4r,选取k0∈N使得2k0r≤t<2k0+1r,由条件(1)和(2)可知，对于任意的x∈B，有

首先估计J1,由Hölder不等式可得

对于J2,由2k0r≤t<2k0+1r,x∈B,y1∈(2k0B)c可得|x-y1|～|xB-y1|.因此,由引理2可得

对于J3,类似于J2的估计可得

J3≤Ctα.

现在估计J4.由2k0r≤t<2k0+1r,x∈B,y1,y2∈(2k0B)c可知|x-y1|+|x-y2|～|xB-y1|+|xB-y2|.因此,如果α≥0,取0<ε<δ-α,则由引理2可得

若α<0,同样可得

另一方面,由非卷积型核K的消失性条件(1)和(3)可知,对于任意的x,x′∈B，有

因此,对于任意的x,x′∈B,设n>α+δ,则由文献[15]中引理2.3的证明方法和引理2.2,类似于估计J4可得

至此,完成定理1的证明. 】

下面证明定理2,我们也仅考虑双线性情形,对于m≥3的情形类似可得.下面先给出双线性Littlewood-Paleyg*λ-函数在Lebesgue空间上的结果以及相关的点态估计.

||g*λ(f1,f2)||Lp(Rn)≤C||f1||Lp1(Rn)||f2||Lp2(Rn).

定理2的证明只需证明对于任意fi∈εαi,pi(Rn),i=1,2,如果存在x0∈Rn使得g*λ(f1,f2)(x0)<∞,那么对于任意的球B⊂Rn及x0∈B，有

不失一般性,假设||f1||εα1,p1(Rn)=1,||f2||εα2,p2(Rn)=1,B=B(xB,r)表示以xB为球心、以r为半径的球.对于任意的非负整数k,定义

则由核K的消失性条件(1)可得

其中

首先估计H1.由引理4可得

现在估计H2,H3,H4.由对称性和引理5可知

g*λ,0((f1-m4B(f1))χ(4B)c,(f2-m4B(f2))χ4B)(x)≤C|B|α/n,

因此

H2≤C|B|2α/n,H3≤C|B|2α/n,H4≤C|B|2α/n.

最后估计I5.由非卷积型核K的条件(1)和(2)可知,对于任意的x,x′∈B,有

因此,我们总假设λ∈(4,5).

对于E3,由对称性可知

E3≤C|B|2α/n.

如果α<0,同理可得

至此,完成定理2的证明. 】

[1] LITTLEWOOD J E,PALEY R E A C.Theorems on Fourier series and power series[J].JLondonMathSoc,1931,6(3):230.

[2] LUSIN H.Sur une propriete des fonctions a carre sommable[J].BullCalcuttaMathSoc,1930,20:139.

[3] COIFMAN R R,MEYER Y.On commutators of singular integrals and bilinear singular integrals[J].TransAmerMathSoc,1975,212:315.

[5] GRAFAKOS L,TORRES R H.Maximal operator and weighted norm inequalities for multilinear singular integrals[J].IndianaUnivMathJ,2002,51(5):1261.

[7] YABUTA K.A multilinearization of Littlewood-Paley’sg-function and Carleson measures[J].TohokuMathJ,1982,34(2):251.

[8] SATO S,YABUTA K.Multilinearized Littlewood-Paley operators[J].SciMathJpn,2002,55(3):447.

[9] HART J.Bilinear square functions and vector-valued Calderón-Zygmund operators[J].JFourierAnalAppl,2012,18(6):1291.

[10] SHI Shao-guang,XUE Qing-ying,YABUTA K.On the boundedness of multilinear Littlewood-Paleyg*λ-function[J].JMathPuresAppl,2014,101(3):394.

[11] 王斯雷,陈杰诚.关于平方函数的几点注记[J].数学年刊A辑,1990,11(5):630.

[12] SUN Yong-zhong.On the existence and boundedness of square function operators on Campanato spaces[J].NagoyaMathJ,2004,173:139.

[13] YABUTA K.Existence and boundedness ofg*λ-function and Marcinkiewicz functions on Campanato spaces[J].SciMathJpn,2004,59(1):93.

[14] HU Guo-en,MENG Yan,YANG Da-chun.Estimate for Marcinkiewic integrals in BMO and Campanato spaces[J].GlasgowMathJ,2007,49(2):167.

[15] HE Sha,XUE Qing-ying,MEI Ting,et al.Existence and boundedness of multilinear Littlewood-Paley operators on Campanato spaces[J].JMathAnalAppl,2015,432(1):86.

[16] CAMPANATOS.Proprietdi hölderianitdi alcune classi di funzioni[J].AnnScuolaNormsupPisa,1963,17(3):175.

[17] COIFMAN R R,ROCHBERG R.Another characterization of BMO[J].ProcAmerMathSoc,1980,79(2):2494.

[18] STEIN E M.On the functions of Littlewood-Paley,Lusin and Marcinkiewicz[J].TransAmerMathSoc,1958,88(2):430.

[19] XUE Qing-ying,YAN Jing-quan.On multilinear square function and its applications to multilinear Littlewood-Paley operators with non-convolution type kernels[J].JMathAnalAppl,2015,422(2):1342.

[20] FABES E B,JOHNSON R L,NERI U.Spaces of harmonic functions representable by Poisson integrals of functions in BMO and [J].IndianaUnivMathJ,1976,25(2):159.