影剧院观众厅上送下回气流分布形式的数值模拟研究

孙 斌，谌 华，杨 迪

(东北电力大学 能源与动力工程学院，吉林 吉林 132000)

随着经济的增长和生活水平的提高，人们对文化生活的要求也日益提高.影剧院作为传播文化的重要场所，舒适的影剧观赏环境是观众的迫切需求，这就需要合理的气流组织来创造舒适的热环境.影剧院观众厅是典型的高大空间，其内部空气流动远比一般建筑复杂，工程上此类建筑的气流组织设计难点在于如何快速而准确的预测内部空气流动，从而制定最优气流组织方案.因为影剧院观众厅人员、灯光负荷分布和送、回风口布置不同等复杂情况，传统的射流分析法因本身的局限性将不能适用.由于计算流体动力学(Computational Fluid Dynamics,CFD)方法成本低、速度快、资料完备，故其逐渐受到人们的青睐，CFD方法便越来越多地应用于暖通空调领域[1].

尽管CFD方法已经大量应用于室内环境，但是只有少量研究涉及影剧院.在影剧院空调设计中，上送下回的气流组织形式因气流分布均匀、地面不易扬尘和美观等优点被广泛采用.因此，深入研究和优化此类气流分布形式对于工程设计具有重要意义.本文采用CFD方法，针对大空间工程效率和精度的特点，选用零方程湍流模型，以江西某影剧院为研究对象，对其气流组织形式进行数值模拟，找出原空调方案的问题并提出了气流组织优化方案，研究方法和结论为影剧院类建筑的空调设计和气流组织优化等提供了理论依据和指导方法.

1 研究对象

本文以江西省井冈山市某影剧院观众厅为研究对象，观众厅有四层通高，长约32 m，宽约29 m，可容纳1 200人，池座720人，楼座480人，为典型大空间.整个观众厅合围在建筑内部，无外墙.由于空间较大，观众厅由两套全空气空调系统共同调节，夏季室内设计温度为25 ℃，相对湿度为60%，气流组织为普遍使用的上送下回形式.限于篇幅，本文仅对夏季工况进行气流组织模拟.

2 数值模拟

2.1 数学模型

2.1.1 零方程模型

本文采用的零方程模型，是Chen等提出的一种新零方程模型，专门用来简化通风空调房间气流组织数值模拟问题[3]，现对这种零方程模型进行简要介绍.

基于混合长度理论[18]，Prandtl做出假设，提出计算湍流粘度μt的表达式：

(1)

式中：c为经验常数；ρ为密度；K为湍流动能；l为湍流脉动长度尺度.此式表明湍流黏度与湍流动能K和湍流脉动长度尺度l有关.

Chen等在上述表达式的基础上，提出一个简单的代数方程式来表示湍流粘度，即

μt=0.038 74ρv，

(2)

式中：0.038 74为经验常数；v为当地时均速度.将湍流黏度看作当地时均速度和长度尺度的函数，其中长度尺度被定义为与最近壁面的距离.结合通用方程，便可求解.

2.1.2 通用方程

任何流体流动都满足质量守恒、动量守恒和能量守恒方程，这三大方程是解决流体力学问题的基础和通用方程.

连续性方程：

(3)

动量守恒方程：

(4)

能量守恒方程：

(5)

2.1.3 模型验证

图1 建筑模型和测点布置示意图

众所周知，空调房内的空气流动为自然对流与强迫对流共存的非等温、混合对流形式，对于此类对流形式，国内外研究表明，零方程模型比工程上常用的标准k-ɛ更准确，赵彬等在通风空调气流组织模拟中采用该模型，已在空调小室中进行对比验证[19].由于高大空间的特殊性，本文对零方程模型再次进行验证.

本文选取文献[20]中的高大空间喷口侧送侧回实验数据进行验证，湍流模型采用零方程，物理模型和所有边界条件均与文献[20]中一致，建筑模型和测点分布如图1所示.测点具体位置和文献[20]中一致，模拟结果列入表1中，实验值与模拟值的比较见图2、图3.从图2、图3中可以看出，模拟值误差不超过5%.经验证，高大空间气流组织数值模拟采用零方程模型完全满足工程精度.

表1 测点模拟值

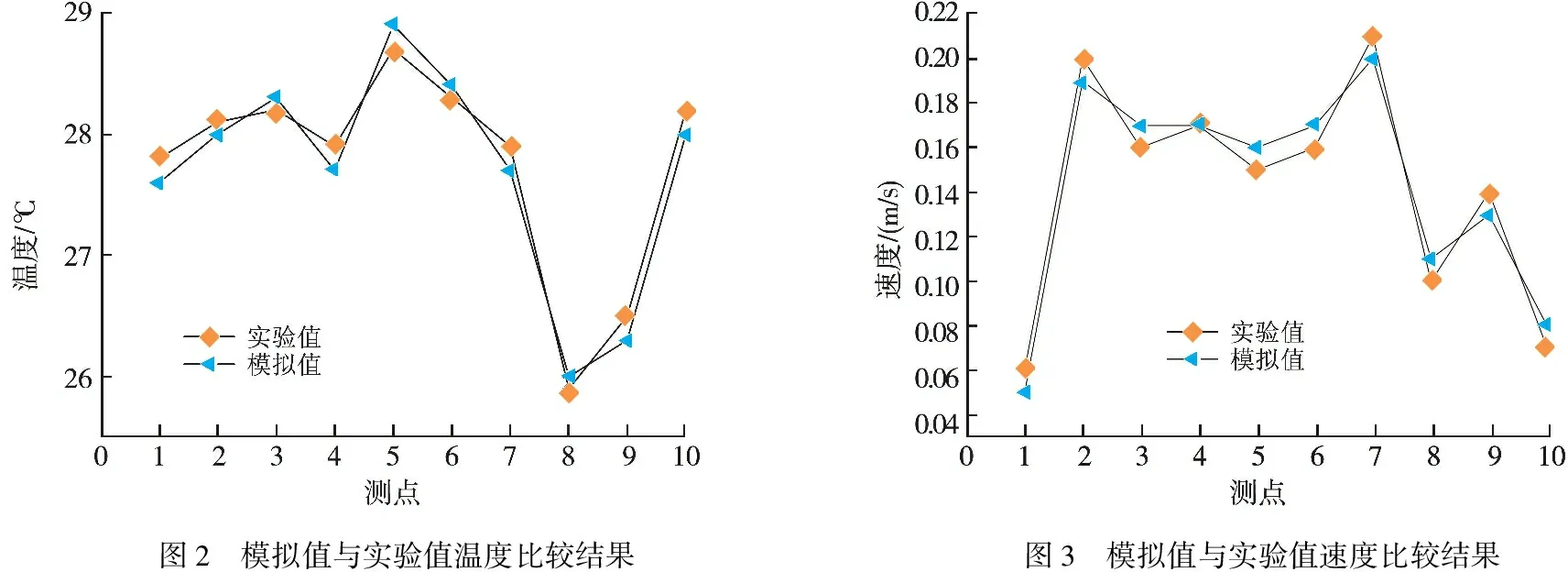
图2 模拟值与实验值温度比较结果图3 模拟值与实验值速度比较结果

2.2 物理模型

如图4所示，观众厅长32 m，高15.7 m，前半部分向舞台中心渐收，墙的弧线简化为直线，最前端宽14 m.观众厅后半部分宽29 m，吊顶呈斜坡状，迎合阶梯型楼座.4个排风口布置在观众厅前部吊顶，Z方向间距6 m.观众静坐散热全热量96 W/人，每排观众40人，简化为0.3 m×1.2 m×22 m的block模块，因存在过道，按1∶2∶1的比例分割成3块.根据送风口和回风口的位置，建立原方案和改进方案的物理模型.原方案：圆形送风口共56个，直径0.4 m，楼座挑台下布置2排送风口，每排6个，Z方向间距4.6 m，X方向间距3 m，吊顶分8排布置44个送风口，根据吊顶面积均匀分布;回风口对称布置在侧墙，楼座2个，尺寸为1.0 m×1.5 m，池座4个，靠前2个尺寸为1.25 m×2.0 m，靠后2个尺寸为1.0 m×1.5 m，回风口均距地1.0 m安装.改进方案：楼座上空吊顶的送风口改为9个方形散流器，分三排布置，尺寸为0.5 m×0.5 m，X方向间距5.5 m，Z方向间距10 m，池座上空吊顶X=8.8 m处布置一排喷口，共5个，直径0.4 m，喷口Z方向间距4.6 m，挑台下布置两排散流器，共6个，X方向间距4.5 m，池座后部两个回风口改为贴后墙布置，相距12 m，其他布置和原方案相同.两套方案概览，如表2所示.

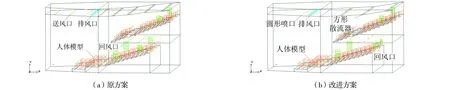
图4 观众厅物理模型图

项目位置原方案改进方案送风口吊顶圆形喷口，直径0．4m单个送风量800m3/h，送风温度15℃前排喷口，直径0．4m单个送风量3800m3/h后排散流器，尺寸0．5m×0．5m单个送风量2400m3/h，送风温度17℃挑台圆形喷口，单个送风量800m3/h，送风温度15℃，直径0．4m方形散流器，单个送风量1600m3/h，送风温度17℃，尺寸0．5m×0．5m回风口楼座单个回风量5000m3/h，尺寸1．0m×1．5m单个回风量5000m3/h，尺寸1．0m×1．5m池座单个回风量：前排10000m3/h，尺寸1．25m×2．0m；后排5000m3/h，尺寸1．0m×1．5m单个回风量：前排10000m3/h，尺寸1．25m×2．0m；后排5000m3/h，尺寸1．0m×1．5m排风口吊顶单个排风3000m3/h维护结构屋顶热流密度10W/m2

2.3 边界条件与网格划分

详细边界条件见表2，表中对围护结构的边界条件进行了合理简化：由于观众厅位于建筑内部，没有外墙，且邻室均设置了空调系统，所以相邻房间的温度基本相同，在工程上可以忽略各房间之间的传热量，所以壁面可认为绝热边界；夏季时，地面也可视为绝热面[21].根据设计数据，屋顶热流密度为10 W/m2.

由于不存在曲面等复杂结构，故采用结构化网格；因为结构化网格在区域边界拟合、网格生产速度、网格质量、数据结构等方面都明显优于非结构化网格.高质量网格应满足以下几点[22]：

(1)每个单元的扭曲度较小，宽高比不大于5∶1；

(2)整个求解域内单元变化是光滑进行的；

(3)网格在求解域内的疏密变化应与被求变量的梯度变化相适应.

本课题采用正六面体结构化网格进行划分，X方向最大尺寸为1.6 m，Y方向最大尺寸为0.785 m，Z方向最大尺寸为1.45m，原方案网格数为1 157 124，改进方案网格数为634 174.收敛条件是各流动方程相对误差为0.001，能量方程相对误差为1×10-6.

2.4 收敛速度比较

为了验证零方程模型效率高的特点，分别用零方程模型和标准k-ɛ模型对原方案的观众厅气流组织进行数值模拟，对比其收敛时间.从表3中可以看出，零方程模型收敛时间基本为标准k-ɛ模型的1/2，节省了近5 h的时间.

表3 零方程模型和标准k-ɛ模型收敛时间

图5 观众上部0.2 m斜面示意图

2.5 模拟结果分析

由于观众席呈阶梯型排布，为了更好的观察观众活动区域的情况，取观众上部0.2 m的斜面进行温度场和速度场的分析，如图5所示；另外选取Z=14.5 m截面，用来观测观众厅垂直方向上温度的变化.

2.5.1 原始方案分析

温度场分析：从图6可以看出，原方案的空调效果并不理想，整个观众厅温度偏低，只有部分区域达到了25 ℃，初步估计是送风温度偏低导致.送风口正下方温度最低，与设计温度相差较多，主要原因是喷口冷风直吹，冷气流不能与周围的热空气进行充分的热交换，使得到达观众席的气流温度过冷.此外，观众厅后部的温度却高于设计温度，主要是由于后部距离吊顶或者挑台太近，尤其是池座后部，座位过于贴近挑台，大部分热气流在此淤积，导致局部温度接近29 ℃.同时，从图6(b)可以看到，池座的温度偏低且分布不均匀，分析图6(c)可知，前厅空间高大，下喷的冷气流在未送到活动区域即发生了弯曲，其原因主要有两个方面，一是送风速度太小，气流射程不够；二是下送的冷气流与上排的热气流相遇，导致冷气流向前偏转，使得空气流动混乱，温度场不能达到预期的均匀效果.此外，原始设计方案中，前厅送风口布置太多，无座区域也进行送风，存在能源浪费.

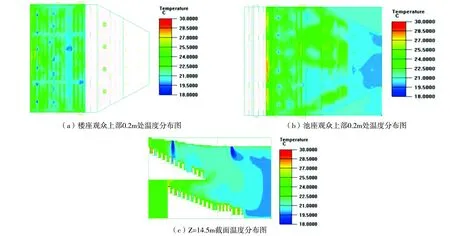
图6 原方案温度场云图

速度场分析：从图7可以看出，原方案速度场绝大部分区域控制得当，风速在0.5 m/s以下.因为原方案送风口数量多，在总风量不变的条件下，单个风口送风量小，所以送风相对均匀.但是在观众厅后排，喷口垂直送风同时也暴露出缺点：后排观众与上部送风口距离太近，且风速衰减的慢，导致冷气流被送到人员活动区域时风速过大.从图7可以看出，观众厅后排喷口正下方的人员活动区域速度场分布最大，风速超过了0.8 m/s，个别区域甚至超过了1 m/s，大大偏离了设计标准.

2.5.2 改进方案分析

温度场分析：从图8可以看到，改进后的气流组织形式使整个观众厅温度保持在25 ℃左右，并且温度场均匀.送风温度增加2 ℃使得观众厅整体温度升高，符合设计温度，楼座和池座顶部送风口改成散流器后，气流分布更均匀.楼座后排温度局部区域稍高，在26 ℃左右，但是仍然在允许偏差范围内.从图8(b)可以看到，池座回风口布置到后排使得热气流及时排出，只有少部分温度稍高但低于27 ℃，满足空调设计.分析图8(c)可知，前厅吊顶的喷口数减少后，送风速度增大，冷气流不受干扰均匀下送，使得前厅温度场均匀且符合设计标准.

图7 原方案速度场云图

图8 改进方案温度场云图

图9 改进方案速度场云图

速度场分析：从图9可以看出，改进方案的速度场很好的满足要求，风速都控制在0.5 m/s以内；同时可以看到，送风口改成散流器后，冷气流不再直吹观众，解决了观众厅后排风速过大的问题.

3 结 论

(1)利用CFD技术对高大空间气流组织进行数值模拟，能准确得出室内温度场和速度场分布，快速找出气流组织存在的缺陷并有效的指导分析和解决问题，同时节约大量的时间、人力和物力.

(2)对于高大空间，CFD方法采用零方程湍流模型比标准k-ɛ湍流模型所用的时间更少，而且不失精准度，工程效率高.

(3)对于采用上送下回气流分布形式的影剧院观众厅的工程设计，提出以下几点建议：

①对于送风口，楼座和池座上部的送风，应尽量使冷气流分散，避免直吹观众，推荐使用散流器等送风口；对于前厅的高大空间，采用喷口送风，风量可以适当增加，以确保冷气流能送到人员活动区，并保持良好的气流组织形式.

②对于回风口，观众厅后墙需设置回风，避免热风在后部聚集.

③送风温度对观众厅内的温度场分布影响很大，应根据设计标准，合理选择送风温度.

[1] 赵彬，李先庭，严启森.用CFD方法指导通风空调设计[J].制冷与空调，2001，1(5)：11-15.

[2] A.D.Gosman，P.V.Nielse.The flow properties in rooms with small ventilation openings[J].Trans ASME Journal of Fluids Engineering，1980，102(3)：316-323.

[3] Chen Qingyan，Xu Weiran.A zero-equation turbulence model for indoor air flow simulation[J].Energy and Building，1998，28(2)：137-144.

[4] 赵彬，李莹，李先庭.人民大会堂大礼堂空调气流组织现状的数值模拟分析与改进[J].建筑热能通风空调，2009，19(4)：5-8.

[5] Qiong Li，Hiroshi Yoshino，Akashi Mochida，et al.CFD study of the thermal environment in an air-conditioned train station building[J].Building and Environment，2009,44(7)：1452-1465.

[6] Pei-Chun Liu，Hsien-Te Lin，Jung-Hua Chou.Evaluation of buoyancy-driven ventilation in atrium buildings using computational fluid dynamics and reduced-scale air model[J].Building and Environment，2009,44(9)：1970-1979.

[7] C.F.Gao，W.L.Lee.Optimized design of floor-based air-conditioners for residential use[J].Building and Environment，2009,44(10)：2080-2088.

[8] 刘学来，李永安，李继志,等.毛细管平面辐射空调室内新风气流组织研究[J].建筑科学，2010，26(10)：197-201.

[9] P.Rohdin，B.Moshfegh.Numerical modelling of industrial indoor environments：a comparison between different turbulence models and supply systems supported by field measurements[J].Building and Environment，2011,46(11)：2365-2374.

[10] C.F.Gao，W.L.Lee.Evaluating the influence of openings configuration on natural ventilation performance of residential units in Hong Kong[J].Building and Environment，2011,46(4)：961-969.

[11] K.C.Ng，M.A.Abdul Aziz，E.Y.K.Ng.On the effect of turbulent intensity towards the accuracy of the zero-equation turbulence model for indoor airflow application[J].Building and Environment，2011,46(1)：82-88.

[12] Shichao Liu，C.M.Mak，Jianlei Niu.Numerical evaluation of louver configuration and ventilation strategies for the windcatcher system[J].Building and Environment，2011,46(8)：1600-1616.

[14] Liang Pu，Fu Xiao，Yanzhong Li，et al.Effects of initial mist conditions on simulation accuracy of humidity distribution in an environmental chamber[J].Building and Environment，2012,47：217-222.

[15] H.Ramy.Mohammed.A simplified method for modeling of round and square ceiling diffusers[J].Building and Environment，2013,64(64)：473-482.

[16] Huijuan Chen，Bahram Moshfegh，Mathias Cehlin.Computational investigation on the factors influencing thermal comfort for impinging jet ventilation[J].Building and Environment，2013,66(50)：29-41.

[17] 陈绕超，何石泉，李丽,等.某音乐厅夏季气流组织数值模拟分析[J].建筑科学，2015，31(4)：129-134.

[18] 陈懋章.粘性流体动力学基础[M].北京：高等教育出版社，2002.

[19] 赵彬，李先庭，彦启森.用零方程湍流模型模拟通风空调室内的空气流动[J].清华大学学报：自然科学版，2001，41(10)：109-113.

[20] 胡定科，荣先成，罗勇.大空间建筑室内气流组织数值模拟与舒适性分析[J].暖通空调，2006，36(5)：12-16.

[21] 孙斌，李英嘉.通风方式对PM2.5颗粒分布影响的模拟研究[J].东北电力大学学报，2017，37(5)：32-37.

[22] 陈焕新.空调列车室内空气品质与气流组织的研究[D].武汉：华中科技大学,2002.