基于VSC的DCIPC在潮流调节中的应用
2018-01-26魏晨晨
李 娟,魏晨晨,2
(1.东北电力大学 电气工程学院,吉林 吉林 132012;2.河南省驻马店供电公司,河南 驻马店 463000)
随着社会经济的飞速发展和用户对电能质量要求的日益提高,大型电网互联已经成为电力系统发展的必然趋势,同时也将是提高电力系统运行可靠性和电能资源配置的重要途径.由于地理位置、输电走廊空间、电网结构等限制,使得输电系统不能通过结构扩建作为解决输电过程中遇到的诸如输电线路过负荷运行、潮流分布不合理、网络损耗增大,联络线功率波动、连锁反应的事故波及、环流等新问题.通过柔性交流输电系统(Flexible Alternative Current Transmission Systems,FACTS)进行联网,可以有效地解决网络损耗过大、潮流分配不合理、电力系统功率振荡[1]等问题.在电力系统中加入FACTS元件并通过电力电子器件控制其参数,为实现潮流控制,降低网络损耗提高网络的功率传输能力提供了一种有效的手段[2~4].
相间功率控制器作为一种典型的串联型器件,其对潮流的控制能力很强,可以有效控制线路功率,改善网络的潮流分布,对电网的经济运行具有一定的影响[5~7].由于IPC在潮流调节中的灵活特性,且IPC具有良好的潮流控制鲁棒性,短路电流限制特性以及两端电网的故障隔离特性,所以将其应用在电网中的程度被逐步扩大和完善,自从其问世以来便被广大研究专家所青睐[8].文献[9]对非调谐型IPC进行了计算和分析,得出非调谐型IPC相对于调谐型IPC的潮流控制鲁棒性较差,限制短路电流的特性也趋向弱化.但是,相对于调谐型IPC它却体现出具有保持同步能力的不同的有功功率控制特性.文献[10]对相间功率控制器的运行状态进行理论数学推导,论证了IPC的运行状态和其本身参数以及连接IPC两端电网的关联参数表达形式,并可以对IPC的选址、潮流优化调节以及IPC的运行特性具有实用的意义.本文以VSC代替传统IPC的移相环节,阐述了电压注入型DCIPC中VSC的调制比M及移相角θ与线路潮流的关系,在此基础上提出间接电流控制策略以实现对VSC的调节控制,并进行仿真且验证在潮流调节方面研究的意义.
1 IPC模型的建立
1.1 IPC基本结构
IPC每相包括两个相移环节,一组并联、独立移相单元的容性和感性支路,共四个可控单元,其单相电路结构如图1所示.图1中Us、Ur分别为IPC入口和出口的电压,δ为IPC入口、出口两侧电压相位角差,Xl、Xc分别为IPC电感、电容元件的等效感抗和容抗.
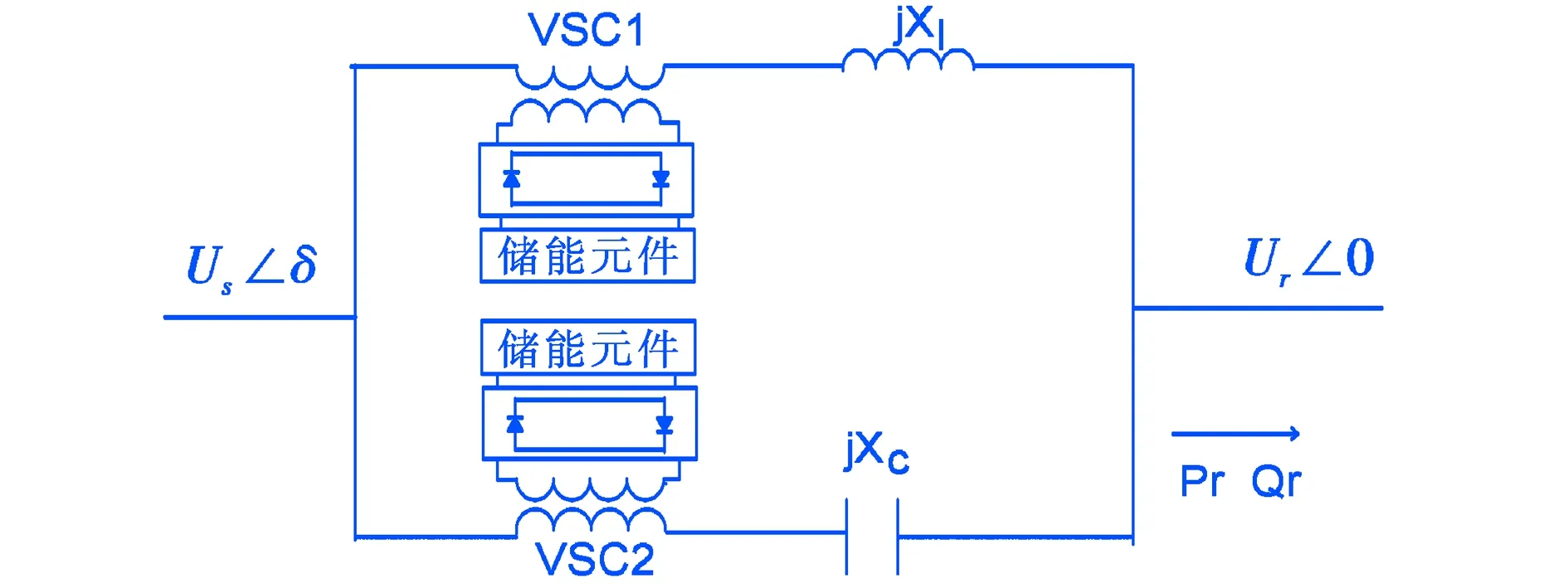
图1 IPC的电路模型
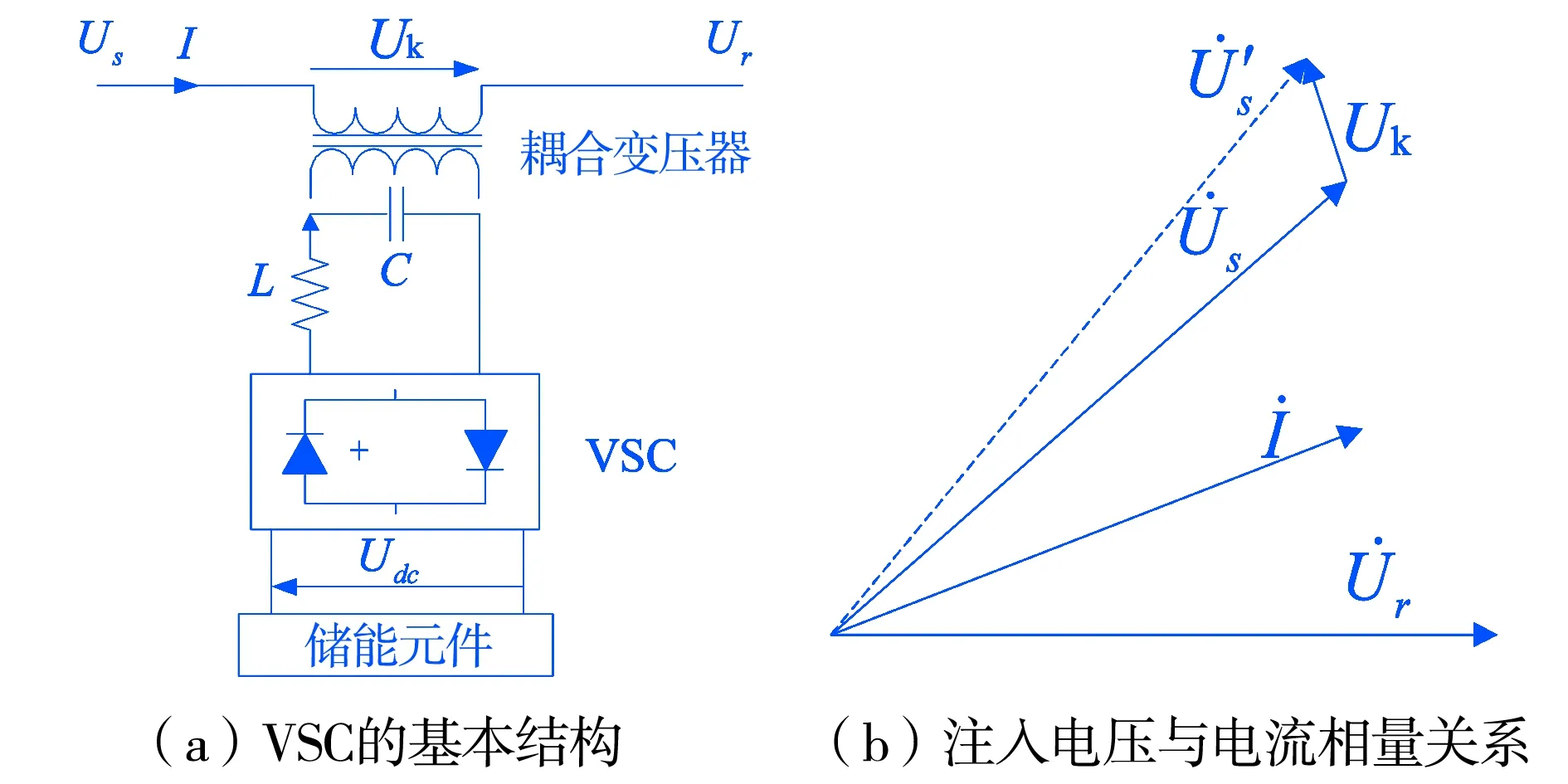
图2 VSC基本结构及注入电压与电流相量关系图
电压源换流器(VSC)是可交直流双向变换,且交流有功功率和无功功率可分别独立控制的电力换流器[11].VSC的基本电压由直流侧并联电容器提供,除自身损耗外,常与系统间不存在有功功率交换,因此其向输电线路注入的电压为近似正弦的,且是与电路电流正交的可控电压.VSC的基本结构及其注电压与线路电流的相量关系,如图2所示.
VSC注入电压Uk(k=1、2)与电流关系相量图虚线部分所示,注入电压使得VSC两端电压的幅值和相位均发生改变,线路的有功功率和无功功率也相应发生改变.
1.2 带有IPC线路的潮流分析
令电感支路和电容支路的注入电压分别为U1、U2,则其表达式为
U1=m1Vdc1ejθ1,U2=m2Vdc2ejθ2.
(1)
式中:m1、m2分别为电压源换流器VSC1、VSC2的调制比;θ1、θ2分别为电压源换流器的移相角度;Vdc1、Vdc2分别为压源换流器直流侧电容电压.
DCIPC电感、电容支路移相后的电压分别为
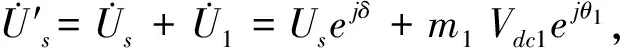
(2)
联络线上的电流
(3)
整理可得:有功功率
(4)
无功功率
(5)
由此可见并入IPC后,线路传输的有功功率和无功功率都与电压源换流器VSC的调制比M和移相角θ有关,因此通过调整IPC中VSC的参数可以控制系统的潮流.
2 VSC的控制策略
2.1 工作原理
IPC中VSC的控制目标是向线路注入一个与支路电流正交的电压,使其呈现电感或电容特性来改变支路的等效阻抗和线路两侧相位差,从而实现对线路传输功率的调节[12].
通过对VSC内部结构和控制原理进行分析,采用间接电流控制策略调节PWM的调制比M和移相角θ,实现对VSC注入电压的控制,从而达到灵活快速地调节交流电压的幅值和相角,进而对电力系统的潮流进行控制.
2.2 间接电流控制机理分析
间接电流控制也称为“直接控制”,实际上就是所谓的“电压幅值相位控制”,也即是通过调节VSC交流侧输出电压基波的幅值和相位来达到控制目标.其主要原理是根据所控制物理量的偏差值输入,直接由比例积分调节器得到相应的调制比M和移相角θ两个物理量,然后将其输入到触发脉冲发生环节以实现对换流器的控制调节,原理如图3所示.其中φ表示系统电压和电流之间的相角差;比例积分调节器中Kp用来提高响应速度,Ki用来消除稳态误差.
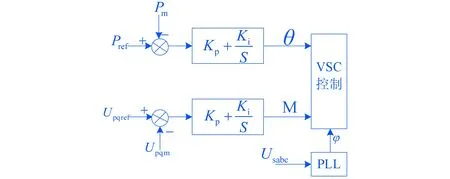
图3 VSC系统间接电流控制原理图
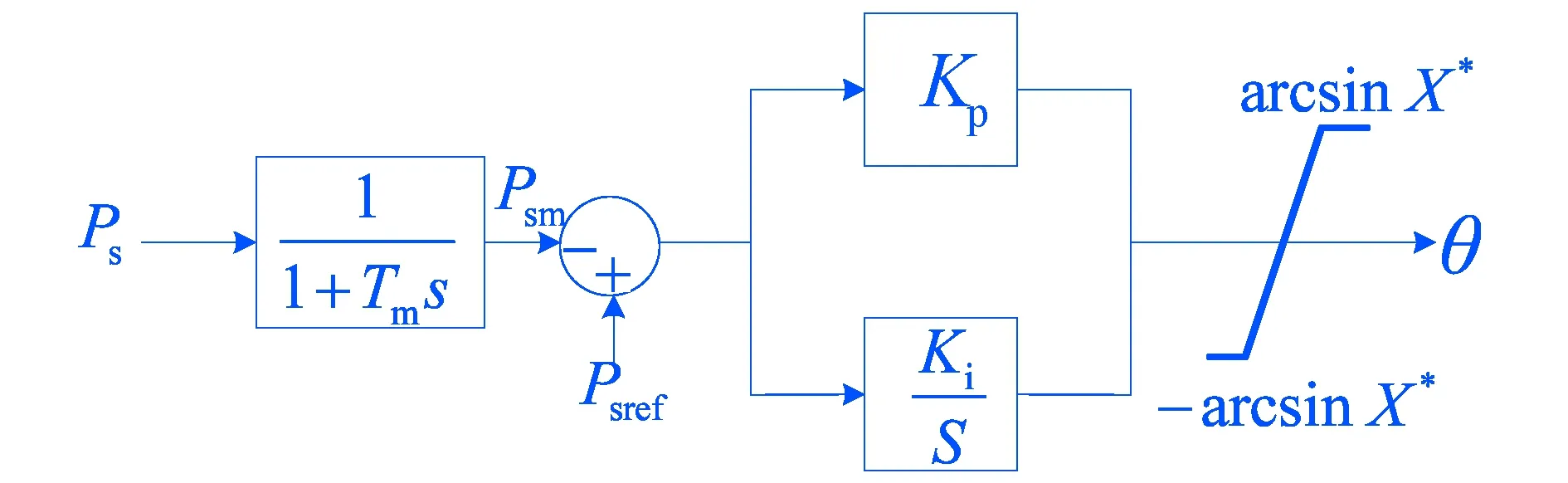
图4 有功功率控制器原理框图
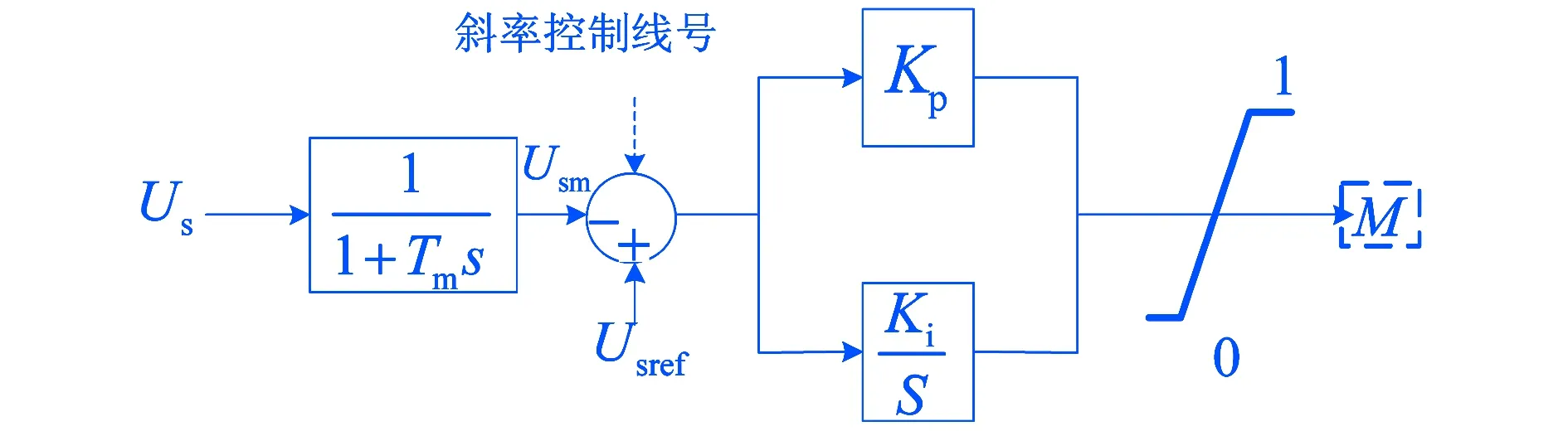
图5 交流电压控制器原理框图
(1)有功功率控制机理分析
有功功率大小与电压的相位密切相关,因此控制交流电压的相角可以调节有功功率.有功功率控制的基本原理是利用有功功率测量值Psm与控制参考值Psref的差值,通过PI调节器来控制调节PWM调制波的移相角θ,以使换流站注入到交流系统的有功功率到达其设定值,其原理如图4所示.当有功功率差值很大时,为防止出现积分饱和现象,需要在积分环节中加入相应的限幅环节;同时为了防止有功功率控制器发生超调现象,在其输出也需要加入移相角限幅环节[13~14].
(2)无功功率控制机理分析
无功功率大小与电压的幅值密切相关,因此控制交流电压的大小可以调节无功功率.无功功率控制的基本原理是利用测量值Usm与参考值Uref的差值,通过PI调节器控制调节PWM调制波的调制比M,以此来改变交流电压的幅值进而改变注入到交流系统的无功功率,如图5所示.
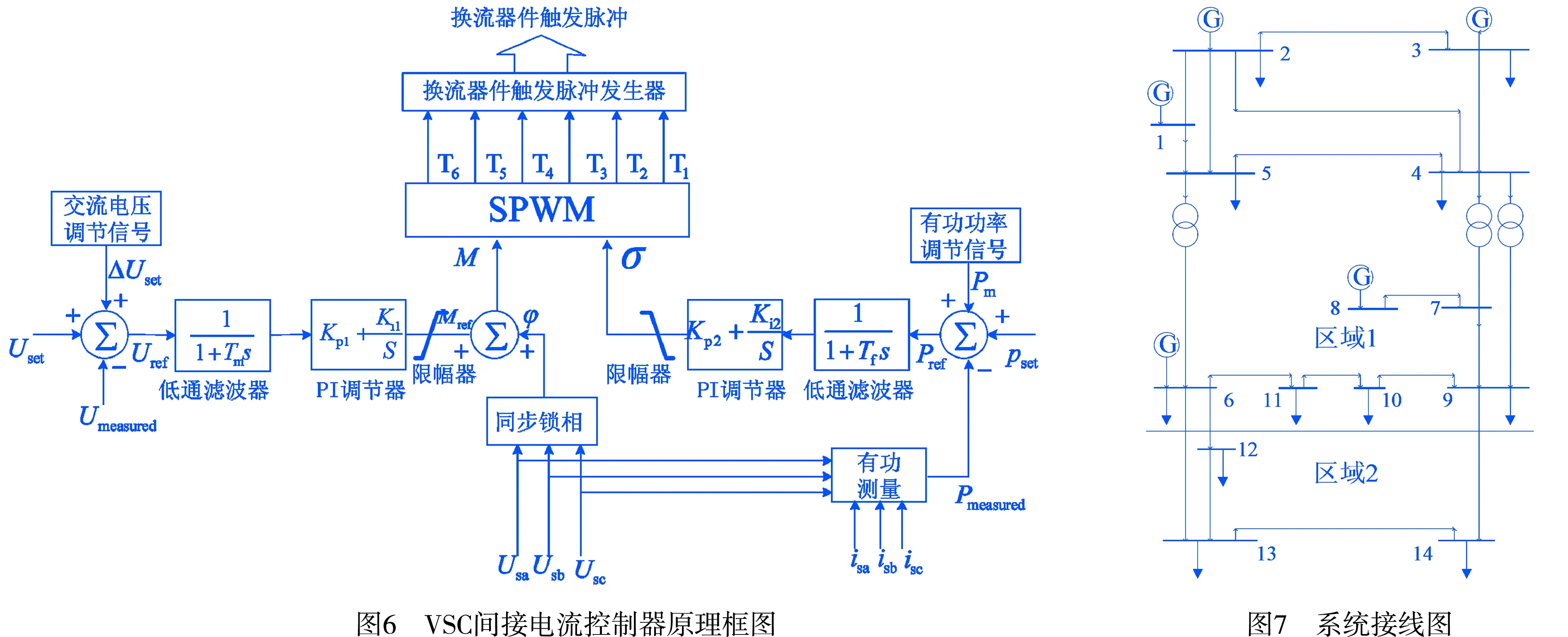
将实时采集的有功功率、交流电压与系统相应输出物理量的参考值之间的偏差,输入到相应的控制模块并经过比例积分调节器,得到与VSC有功功率,交流电压相关基于PWM调制的调制比M、移相角θ,最终根据得到的M与θ生成触发脉冲,进而对电压源换流器中的IGBT阀进行控制.依据上述间接电流控制的原理,得到换流器的间接电流控制原理,如图6所示.图6中,换流阀采用正弦脉宽调制(Sinusoidal Polse Width Modu lation,SPWM)正脉宽调制,T1~T6为开关器件的脉冲触发信号.
3 算例分析
以IEEE14节点系统为例(系统接线图如图7所示),该系统共含有5台发电机,其中1号节点为平衡节点,节点2、节点3、节点6、节点8为PV节点,节点4、节点5、节点7、节点9、节点10、节点11、节点12、节点13、节点14为PQ节点.
把IPC并入线路1-5、2-5上,得到无IPC和有IPC的系统潮流,如表1所示.(所有计算结果均以有名值表示)由表1可知功率的环网自然分布使得线路1-2处于重载状态,而线路7-8处于轻载状态,网络潮流分布不合理,容易引起网损增大.并入IPC并对其参数进行控制之后减轻了重载线路的负担,同时轻载线路也适当增强了输送功率的能力.

表1 无IPC和有IPC支路的数据和潮流结果

表2 无IPC和有IPC网络总有功和无功损耗
由表2可知网络中加入IPC之后,系统的有功和无功损耗都有所降低.为了进一步研究IPC中VSC的控制变量M、θ对系统潮流的影响,接下来将分别固定其中一个变量,控制另外一个变量,观测网络潮流的变化.
情况一:将注入电压的幅值固定,保持注入电压的幅值在0.3p.u,使移相角θ在-180°到+180°范围内变化.线路1-5、2-5有功功率的变化,如图8所示.在注入电压一定的情况下,随着移相角度的增大IPC所在线路的有功功率有波动的趋势.线路1-5、2-5无功功率的变化,如图9所示.在注入电压一定的情况下,随着移相角度的增大IPC所在线路的无功功率先减小而后逐渐增大.
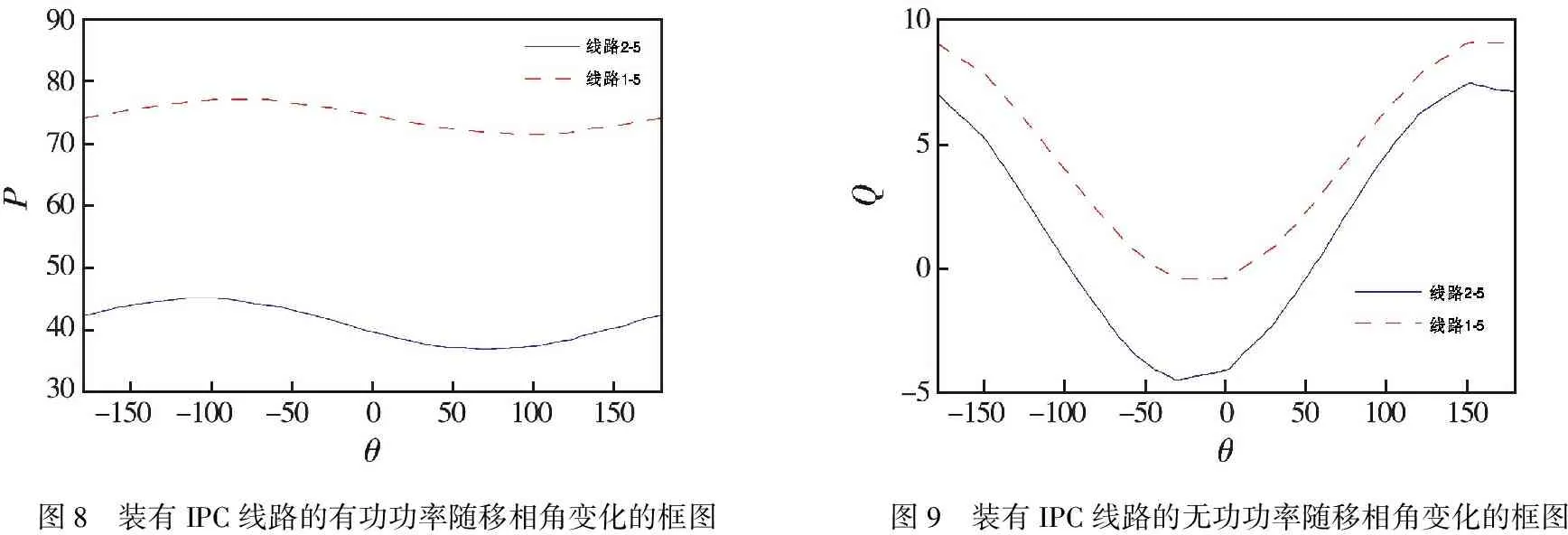
图8 装有IPC线路的有功功率随移相角变化的框图图9 装有IPC线路的无功功率随移相角变化的框图
网络的总有功功率损耗,如图10所示.在注入电压一定的情况下,从-180°到0°随着移相角的增大,总有功功率的损耗也逐渐增加,在0°附近达到最大;从0°到+180°随着移相角的增大,总有功功率损耗逐渐减小.

图10 总有功功率损耗随移相角变化的框图图11 总无功功率损耗随移相角变化的框图
网络的总无功功率损耗,如图11所示.在注入电压一定的情况下,从-180°到+100°随着移相角的增大,总有功功率的损耗减少,在-100°附近达到最小;从-100°到+70°之间随着移相角的增大,总有功功率损耗也随之增加;从+70°到+180°之间随着移相角的增大逐渐减小.
情况二:将移相角θ固定,使注入电压的幅值在0.01p.u~0.3p.u范围内变化.线路1-5、2-5有功功率的变化如图12所示.在移相角一定的情况下,随着注入电压的逐渐增大,IPC所在线路的有功功率有逐渐增大的趋势.
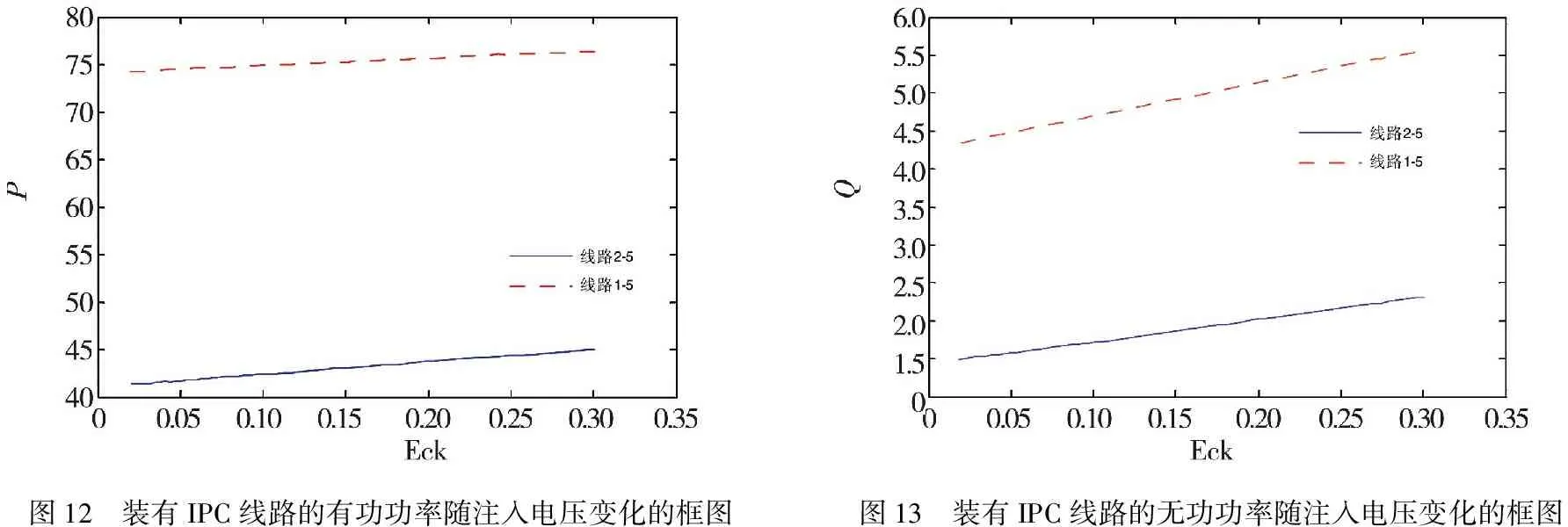
图12 装有IPC线路的有功功率随注入电压变化的框图图13 装有IPC线路的无功功率随注入电压变化的框图
线路1-5、2-5无功功率的变化如图13所示.在移相角一定的情况下,随着注入电压的逐渐增大,IPC所在线路的无功功率有逐渐增大的趋势.网络的总有功功率损耗如图14所示.
在移相角一定的情况下,随着注入电压的逐渐增大,总的有功功率损耗逐渐减小.

图14 总有功功率损耗随注入电压变化的框图图15 总无功功率损耗随移注入电压变化的框图
网络的总无功功率损耗如图15所示.在移相角一定的情况下,随着注入电压的逐渐增大,总的无功功率损耗有逐渐增加的趋势.
情况三:调制比和移相角都发生变化时网络的总有功功率损耗如图16所示.调制比和移相角都发生变化时网络的总无功功率损耗如图17所示.
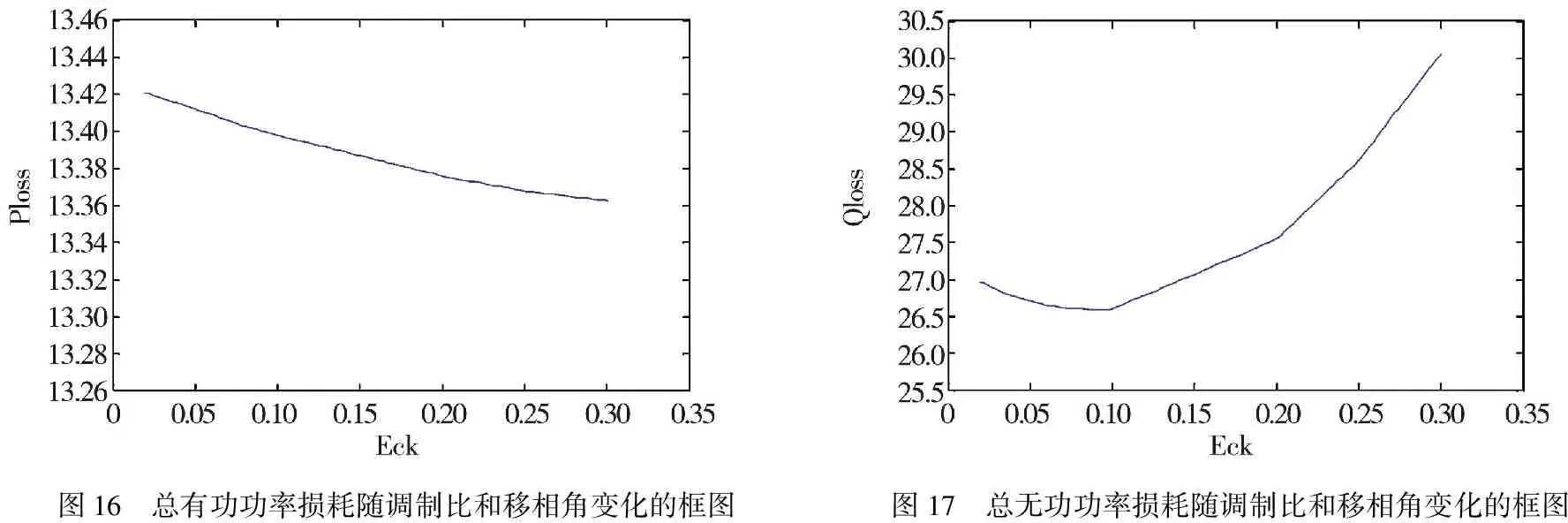
图16 总有功功率损耗随调制比和移相角变化的框图图17 总无功功率损耗随调制比和移相角变化的框图
由图16、图17可知当注入电压和移相角都发生变化时,有功功率和无功功率损耗曲线的趋势和只控制注入电压时大致保持一致.
4 结 论
本文将电压注入型相间功率控制器中的移相环节采用VSC实现构成DCIPC,VSC可以快速灵活地实现改变支路移相角的功能,并且损耗较小.分析了IPC并入系统之后对网络潮流的影响,建立了电压源换流器的控制参数与线路输送潮流的关系式,设计出电压注入型DCIPC中的VSC控制方式,采用间接电流控制对PWM调制的调制比M、移相角θ进行调节.以IEEE14节点算例进行效果验证,通过比较线路中含有IPC前后的线路传输功率大小,以及IPC安装后通过调节VSC的参数,系统潮流的改变情况.分析表明通过控制IPC的变量可以改变功率的分布,提高功率输送能力,对潮流有一定的调节作用.
[1] 袁红斌,张元波,崔国有.浅谈电力系统低频振荡[J].东北电力大学学报,2009,29(1):45-50.
[2] 李娟,赵露,柳焯.基于参数协调的可控相间功率控制器调节特性研究[J].电力自动化设备,2007,27(2):16-19.
[3] 聂宏展,王叫,马方明,等.基于潮流转移识别的紧急减载控制策略研究[J].东北电力大学学,2016,36(4):1-6.
[4] 李娟,纪延超.调谐型相间功率控制器潮流调节能力的分析[J].电力系统及其自动化学报,2002,14(6):52-54.
[5] 刘修宽.蒋维勇,周苏荃.相间功率控制器的潮流调控性能分析[J].电网技术,2006,30(11):11-14.
[6] 李娟,陈晓晋,王坤.基于IPC在潮流调节中的研究应用[J].电工电能新技术,2013,4(2):111-115.
[7] 刘修宽,蒋维勇,周苏荃.IPC增强互联系统稳定性控制策略研究[J].电力自动化设备,2005,25(8):27-31.
[8] 王仲鸿,沈斐,吴铁铮.FACTS技术研究现状及其在中国的应用和发展[J].电力系统自动化,2000,24(23):1-5.
[9] J.Brochu,P.Pelletier,F.Beauregard,et al.The interphase power controller:a new concept for managing power flow within AC networks[J].IEEE Trans.on Power Delivery,1994,9(2):833-841.
[10] Francois Bearegard,Jacques Brochu.Interphase power controller with voltage injection[J].IEEE Transactions on Power Delivery,2011,9(4):1956-1961.
[11] 于继来,柳焯.相间功率控制器的稳态分析及与移相器的特性比较[J].中国电机工程学报,1999,19(8):25-34.
[12] 宋彬彬,赵延青.可控相间功率控制器潮流控制特性研究[J].黑龙江电力,2012,35(5):365-368.
[13] 李娟,闫乃欣,周建颖.TCIPC提高暂态稳定性的PI控制器设计[J].电工电能新技术,2012,33(5):68-72.
[14] M.Farmad,S.Farhangi,G.B.Gharehpetian.Nonlinear controller design for IPC using feedback linearization method[J].International Journal of Electrical Power & Energy Systems,2013,44(1):778-785.
