单摆非线性特征的研究

刘正成，李青松，孙迎春,b

(东北师范大学 a.物理学院；b.物理学师范专业国家级实验教学示范中心，吉林 长春 130024)

单摆是理想的物理模型[1]，其做简谐振动(摆角< 5°)时的运动微分方程为线性方程，具有确定的解析解，其振动周期与摆角无关，是常量；而当单摆做大摆角运动时，运动微分方程为非线性方程，很难用通常的解析方法讨论其运动，不能获得解析解. 对此，文献[2]利用谱分析的方法分析大位移单摆的运动，从理论上获得了大摆角单摆频谱响应的相关参量，结果显示了其运动具有非线性特性[2]. 已有的对单摆非线性运动的讨论多限于理论层面[3-5]，且多采用多项式展开后取近似的手段研究单摆的周期[6-8]. Matlab软件具有强大的计算功能，可以求出非线性方程的数值解[9-11]，因此，可模拟不同情况下单摆的运动. 同时，利用改进的单摆实验装置进行精准测量，可以获得摆角与周期的关系. 将Matlab软件模拟的结果与实验结果对比分析，充分证明了大摆角单摆具有典型的非线性特征.

1 大摆角单摆非线性的理论探讨

1.1 单摆运动动力学方程的建立

用一不可伸长的轻质线绳悬挂一小球(见图1)，当θ<5°时的运动就是单摆. 设小球的质量为m，其质心到摆的固定悬挂点O的距离为l(即摆长). 由受力分析可知，作用在小球上的切向力的大小为mgsinθ，它总是指向平衡点O′. 依据牛顿第二定律，单摆的运动方程为

ma切+mgsinθ=0.

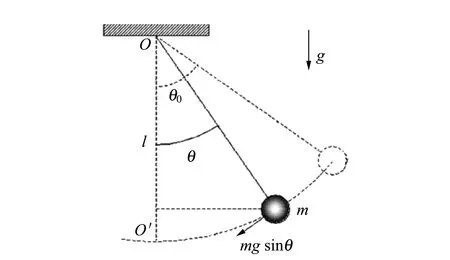
图1 单摆运动示意图

其中

则

即

(1)

式(1)即为单摆在任意摆角情况下的动力学方程，用通常手段很难求出其精确的解析解，往往需进行多项式展开后取近似，所以，无法直接获得θ与周期T的关系.

1.2 利用Matlab软件求大摆角单摆运动方程的数值解

(2)

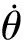
(a)

(b)图2 摆角θ与角速度随时间变化的时域图 (θ0为起始摆角)

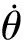
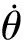
(a)

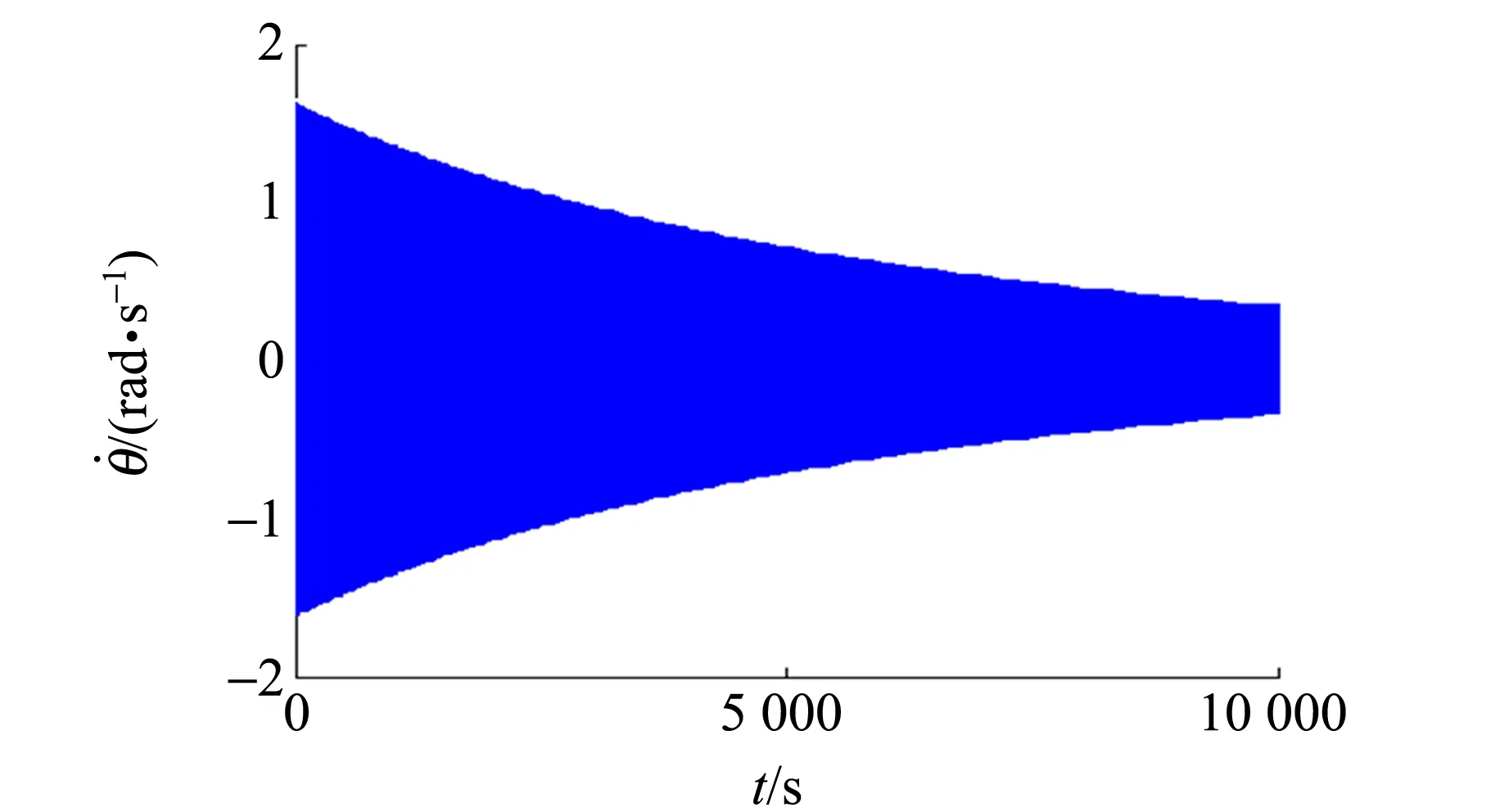
(b)图3 θ和在10 000 s内幅值随时间的变化

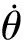
(a)10 s

(b)10 000 s图4 实时θ与相位关系的平面相图

(a)10 s

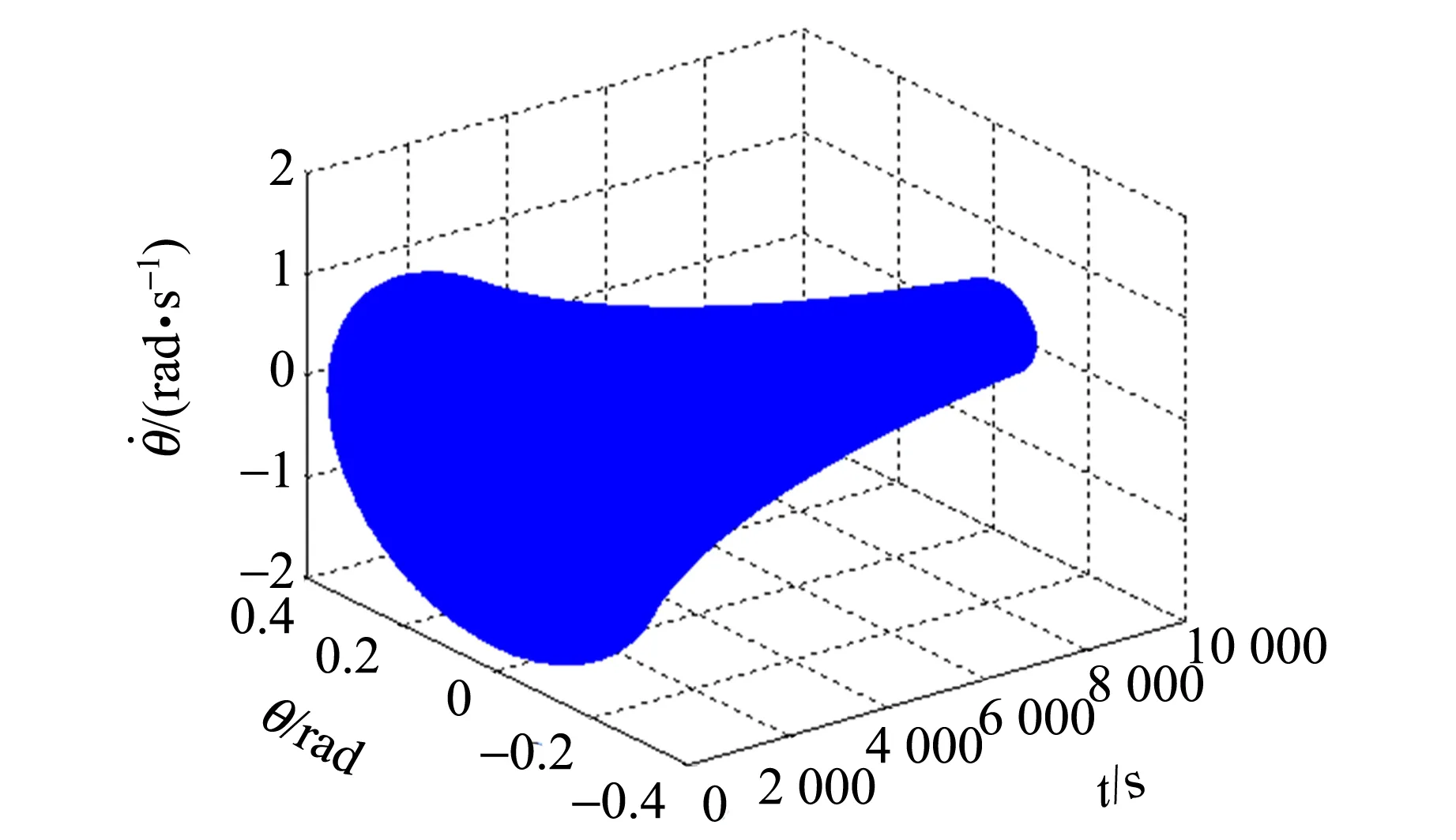
(b)10 000 s图5 实时的θ与相位关系的立体相图

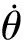
对图2中的各个θ0和T进行统计，获得了θ幅值和T随单摆摆动次数N变化的规律如图6所示. 结果表明：无论θ0多大，振荡的峰值和T都随时间缓慢减小，但T大小是在一个范围内起伏变化[见图6(b)中放大的部分].

(a)θ-N

(b)T-N图6 θ和T随单摆摆动次数N的变化关系图

2 大摆角单摆的实验研究

2.1 改进的精准测量实验装置

在通常单摆装置上，上下各添加固定1个钢直尺，用于准确控制θ0的大小. 在实验装置模式图中(见图7)，S1是单摆固定悬梁的位置，钢尺1放置在与光电门中心且正交的方向上，S2是钢尺2的高度位置(可在杆上滑动)，变换单摆角度即通过移动钢尺2的位置来实现，其好处是可以将选取的角度转换成直角三角形边长的关系，能够更准确地控制θ0. 把摆锤拉到2个钢尺交叉的点处释放，用数字计时计数测定仪测量T. 每个θ0下测量1个周期5次，结果取算术平均值(用cos函数来计算每个角度).

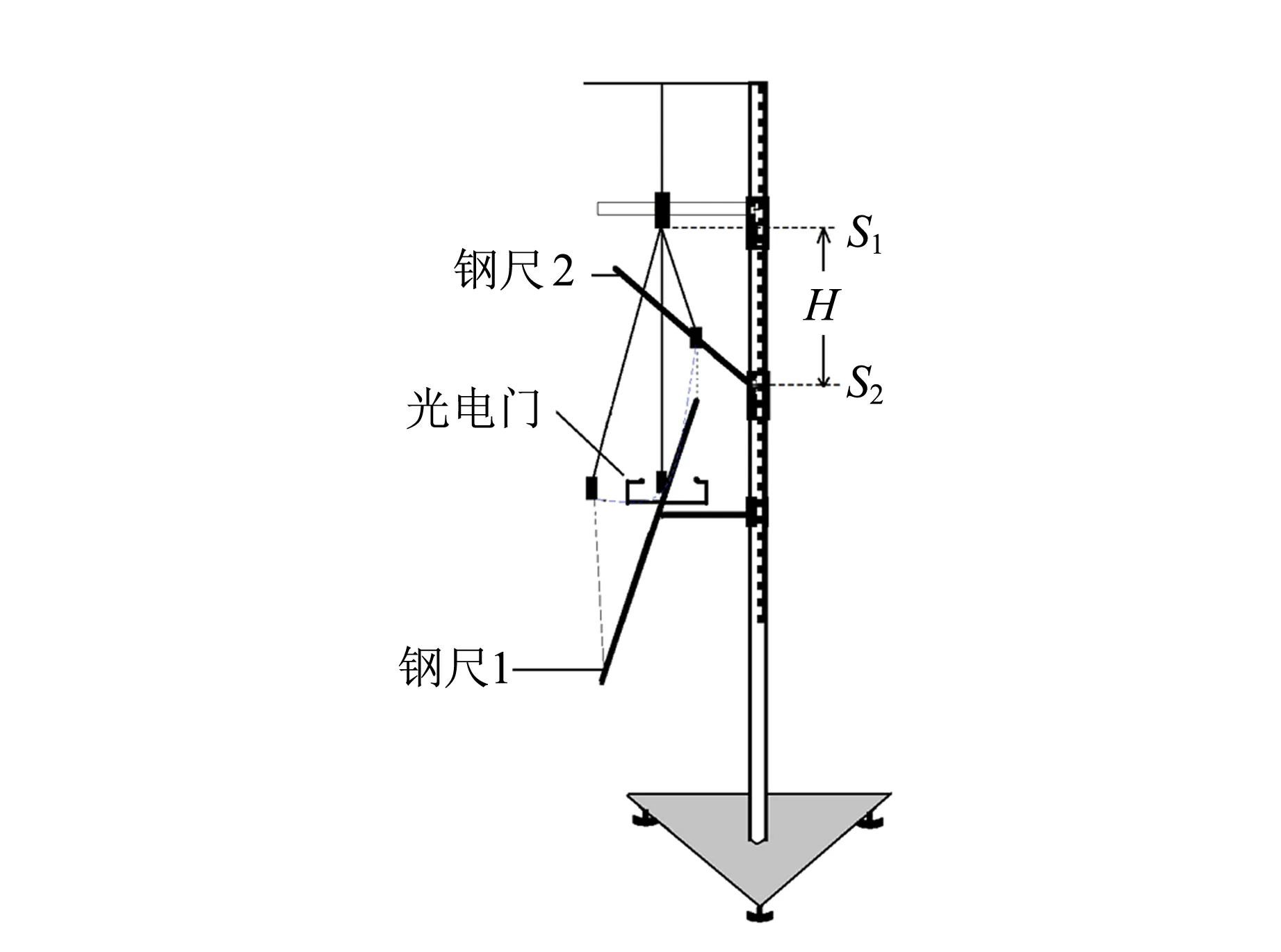
图7 改进的单摆实验装置模式图

2.2 实验测量与分析

由于实验条件的可控性和模拟时θ0可随意的选择性，因此，选择了模拟计算和实验测量θ0相同. 为了更直观地获得二者的对比结果，借助于Origin软件作图(见图8)，可见二者吻合较好，曲线趋势走向一致.θ0≤50°时，理论模拟和实验测量结果几乎完全重合，但当θ0>50°时，实验测量值小于理论模拟值，具有0.2%的相对偏差，这可能是由于以下原因造成：钢直尺的精度低引入的误差，实验测量时空气阻力等引入的误差，实验测量时操作人的操作引入的误差，测时仪器引入的误差等.

图8 T与θ0关系的实验值与理论值对比关系

3 结束语

从单摆运动的动力学理论方程出发，求解出了θ和T的数值解，并模拟出二者随时间的变化规律，获得了θ幅值随时间增加而减小，T虽然也减小但呈现出不规则性的结果. 通过改进的实验设备，对大摆角单摆的T进行精准测量，发现获得的结果与理论模拟结果一致，因此，从理论和实验两方面证实了大摆角单摆的非线性特征.

[1] 王海期. 非线性振动[M]. 北京：高等教育出版社， 1992：262-278.

[2] 马汝建，王均刚，赵东. 大位移单摆的非线性分析[C]//第九届全国振动理论及应用学术会议论文集. 杭州：浙江大学出版社，2007：182-185.

[3] 袁钢. 单摆实验研究与分析[J]. 六盘水师范高等专科学校学报,2007，19(6)：19-20.

[4] 李元杰. 单摆的规则、随机与混沌运动的研究[J]. 大学物理，1998,17(9)：6-8.

[5] 王来英，薛亚宏. 一类基于Matlab的微分方程边值问题数值解的算法研究[J]. 中国西部科技,2012，11(8)：48-50.

[6] 谭志中. 求大摆角单摆周期近似解的“局部常化”方法[J]. 大学物理，2005,24(12)：14-17.

[7] 龚善初. 利用线化和校正法求非线性单摆运动的周期[J]. 大学物理，2006,25(2)：16-18.

[8] 李鹏松，孙维鹏，吴柏生. 单摆大振幅振动的解析逼近解[J]. 振动与冲击，2008,27(2):72-74.

[9] 邹丽娜，程丽红，程彦明，等. 单摆非线性振动的计算机辅助测量[J]. 物理实验，2001，21(8)：23-25.

[10] 李硕，赵彤帆，李根全，等. Matlab软件在单摆自由振动中的应用[J]. 实验室研究与探索，2013,12(11)：65-68.

[11] 谢宁，高志华，孙迎春. 利用波耳共振仪研究受迫振动的非线性特性[J]. 物理实验，2016，36(2)：15-18.

[12] 秦鸣雷，肖一凡，杨海，等. 大角度下阻尼对单摆振动周期的影响[J]. 物理实验，2012，32(5)：42-45.

[13] 张才国，关小泉，吴森，等. 气轨上单摆的混沌实验[J]. 物理实验，2001,21(6):12-14.