频率共振法在飞机结构疲劳损伤预测中的可行性研究

薛九天，饶德

(1.贵州理工学院航空航天工程学院，贵阳贵阳，550003；2.中国商用飞机有限责任公司民用飞机试飞中心，上海，200232）

0 引言

保证飞机结构在服役中的安全可靠性对保障民航客机的运载安全，保持良好的完好性和充分发挥使用效能具有重要意义[1]。然而，目前飞机结构安全使用的可靠度仍未达到强度、刚度要求，飞机结构的飞行安全仍是一类迄今未从根本上解决的世界性难题，其主要原因就是对飞机结构损伤的复杂性认识不足以及缺少飞机使用过程中结构安全检测的实用技术手段。

尽管国内外航空界对飞机结构安全普遍认识和关注度越来越高，但由于飞机结构损伤导致的航空事故依然占很大比例。1988年4月Aloha航空公司243号航班事故的发生让科学界重新反思如何有效地解决飞机结构的安全检测问题。243号航班事件后，根据NTSB的调查结果显示，事故是由裂缝氧化导致的金属疲劳引起（飞机经常在带盐水的空气环境下操作）。裂痕的位置位于登机门附近，此裂痕很可能就是飞机经过89,090次飞行所造成的金属疲劳[2]。客机在执行每次飞行任务时，客舱都要经历一次增减压的过程，客舱的蒙皮承受交变载荷作用，在多次飞行后，外部铝蒙皮会产生疲劳裂纹，当疲劳累积损伤造成的裂纹扩展至临界裂纹长度后就会快速失稳扩展，最后导致结构破坏，这种结构破坏是造成空难事故的重要原因之一。

对于飞机结构，一方面要求高疲劳强度，另一方面又希望结构重量不能太大。这一矛盾的要求致使必须找出飞机结构的安全等级，必须探寻出有效的方法去预测疲劳状态下结构安全的临界值，包括由于累积疲劳引起的突然性承受能力下降[3]。通常飞机运营方在一定的累计飞行时间或一定次数的起降后，必须进行结构疲劳损伤的检查，结构检查主要包括机体疲劳裂纹和腐蚀的检查。疲劳状态下，飞机结构合金物理-机械性能会发生改变。如果能找出恰当实用的无损检测方法来表征这些逐步发生变化的性能，就可以相应地预测出飞机结构承载能力下降的程度。

国内外学者对疲劳损伤理论提出各具特色的理论和计算模型，通过建立疲劳损伤宏观力学反应量之间关系的方法来描述疲劳损伤演变规律，但由于这些模型应用条件复杂或有较强的理论性，在解决飞机结构在复杂非规律性的不稳定变载荷作用下的实际工程疲劳问题时，有一定的局限性[4]。

本文提出的用频率共振法来解决飞机结构合金疲劳问题，采用局部感应法[5]，通过数据计算来控制表征疲劳损伤量，对飞机结构安全和可靠性的预测具有重要的工程意义。

1 方法介绍

疲劳试验分两部分，第一部分需要对实验样品在特定的载荷下完成预设定的周期性振动，这部分通过测试机完成。测试机的主要部件有：加载连接端，冲程杆，连接杆，电动机，计数器，夹钳和支架。实验样品被两端固定在测试机上，一端被加紧固定，另一端被加载连接端固定并施以载荷。通过调节冲程杆的作用长度可以控制对样品施加的载荷的大小。其动力学原理图如图1所示。

疲劳实验的第二部分将对完成周期性振动后的样品进行表层局部感应，扫描器原理如图2所示。

信号发生器产生特定频率的信号通过A路和B路，A路信号直接进入立体声道声卡（双路信号源输入），B路信号通过检测样品表层状态的扫描仪后发生频率共振并得到一个反馈信号，该反馈信号通过C路进入声卡，比较A路的原信号和C路的反馈信号可以得到两种信号的相位偏移角，相位偏移角是共振法中主要表征材料疲劳损伤的参量。感应扫描仪如图3所示,其原理如图4所示。信号发生器产生的特定频率的信号进入扫描仪压电效应杆下部分后，通过感应接触区2与样品1反生频率共振产生微振幅，在微振幅的作用下压电效应杆上半部分发生压电效应，从而得到发生了相位偏移角的反馈信号。

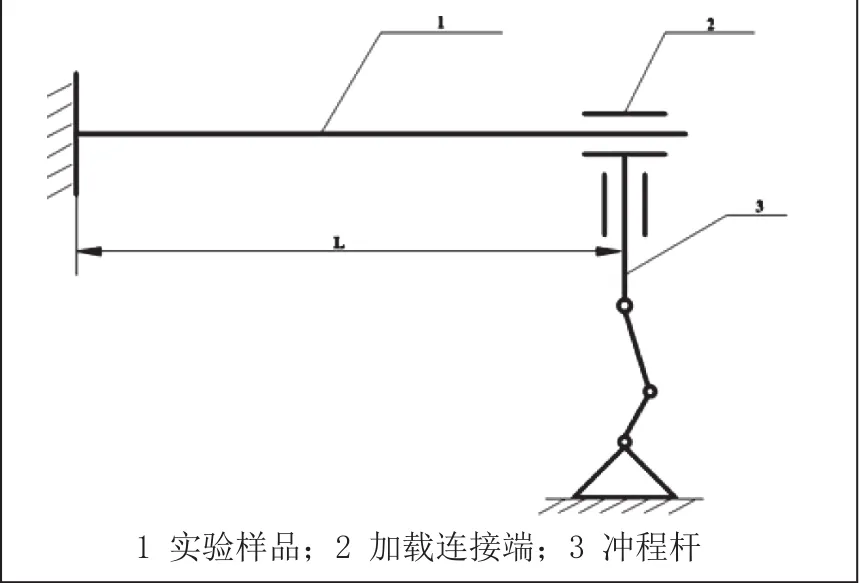
图1 测试机动力学原理图

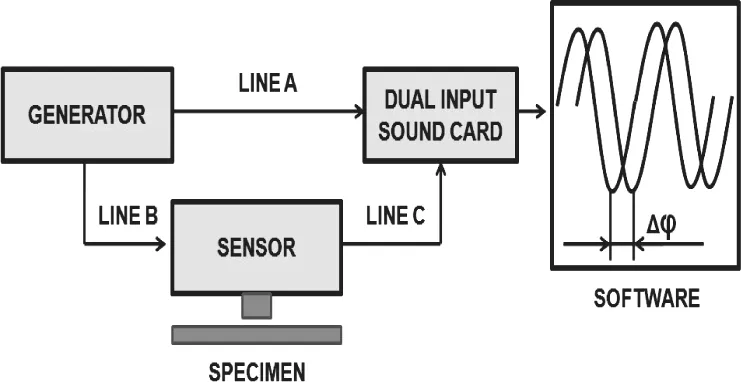
图2 扫描仪原理图

图3 感应扫描仪

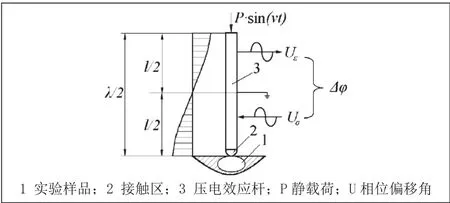
图4 扫描仪原理图

2 实验样品

实验样品为钢 12H18N10T，长 70mm，宽 10mm，厚 1mm。分为两种状态，一种是无孔样品，另一种是带孔样品，其孔的直径为1mm。对于无孔样品，测试点分布在两条不同的直线上，对应两种不同的应力状态，有利于观察不同应力状态下的疲劳损伤情况。而对于带孔样品，其测试点均布在孔的两边，由于应力集中，裂纹将沿着应力集中孔产生，有利于直接观测断裂处的疲劳状态。

3 实验结果分析

3.1 无孔样品结果分析

为了研究疲劳状态下，不同应力对材料结构微变的影响，对无孔样品采取控制两条测试线的方案，第一条测试线距固定端4mm，第二条测试线距固定端14mm。主要实验参量如表1所示。

根据上述法案的规定，可再生能源发电量在总发电量中所占份额到2030年将达到60%(目前的目标为50%)，零售电力到2045年将全部来自可再生能源及其他零碳排放能源。

表1 无孔样品实验参量

实验的第一个任务是探寻不同应力状态下的两条测试线的相似性，其中相位偏移角（SD）为比较参量。相位偏移角（SD）与振动周期数(N)的关系如图5和图6所示。

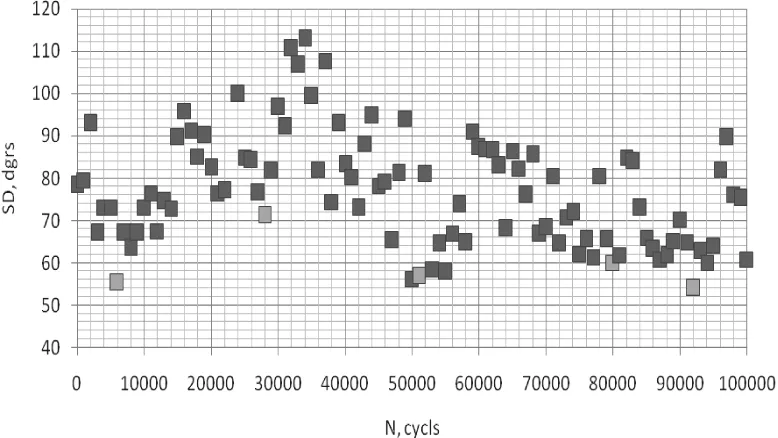
图5 1号样品490MPa下相位偏移角与振动周期数的关系

图6 1号样品415MPa下相位偏移角与振动周期数的关系

图中可以发现一定的相似性趋势，选取一些能表征整体趋势的点比较振动周期数N490和N415，结果如图7所示。

图中可以发现两条应力线是一种近乎线性的关系，方程如下：

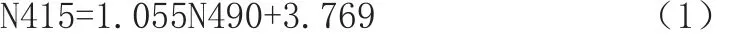
线性回归系数R²=0.969。

类似于1号实验样品，2号样品不同应力状态的两条测试线也具备相似性，其SD与N的关系如图8和图9所示。

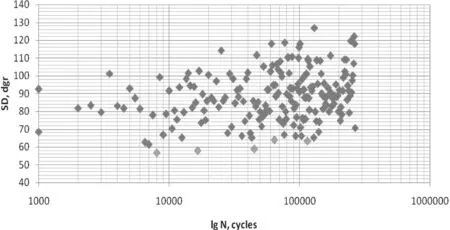
图7 1号样品两条应力线趋势表征点的关系

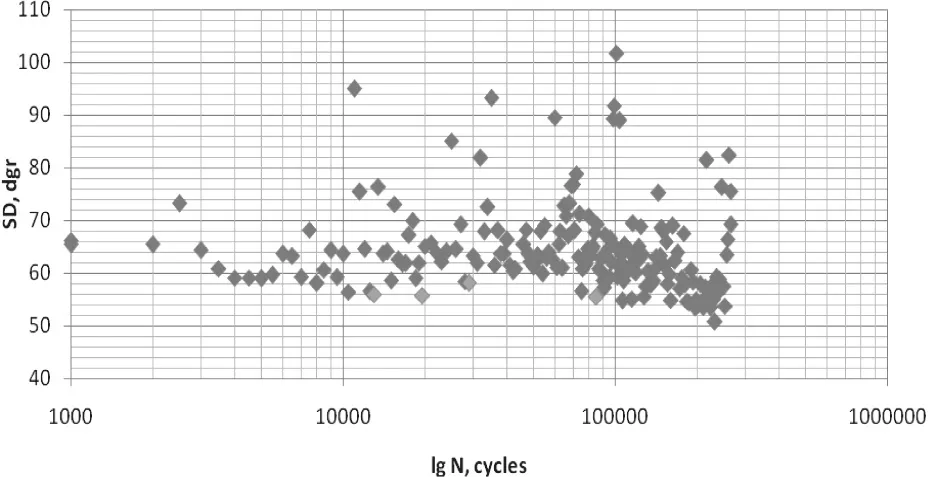
图8 2号样品620MPa下相位偏移角与振动周期数的关系

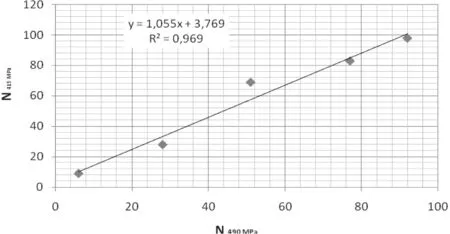
图9 2号样品526MPa下相位偏移角与振动周期数的关系

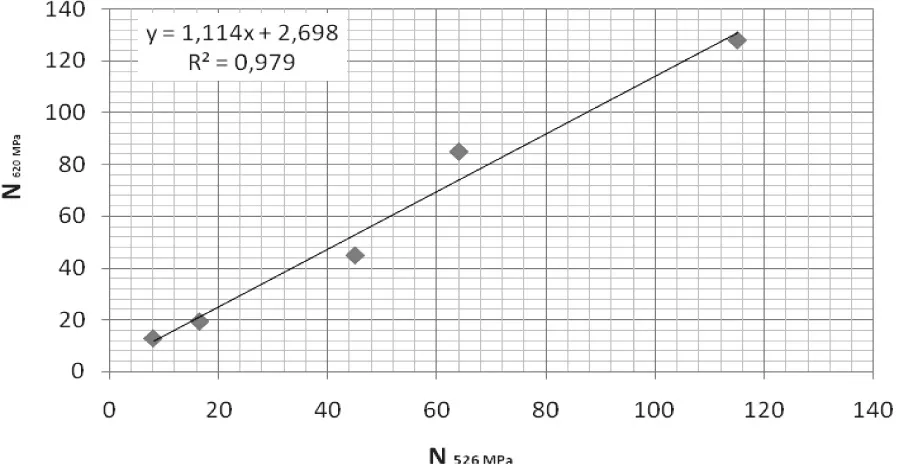
图10 2号样品两条应力线趋势表征点的关系

对于2号样品，同样发现了一些代表点来比较振动周期数N620和N526的关系，如图-10所示。

线性方程为：

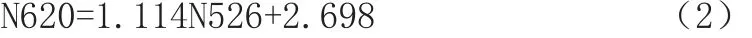
线性回归系数R²=0.979。

显而易见，不同应力区的测试具有相似性，从而佐证了共振法对于探测疲劳状态下材料结构微变的可行性。

3.2 带孔样品结果分析

1和2号样品有一个缺陷，他们的测试结果无法直接表征材料断裂处的疲劳状态，因为无孔试样在固定端断裂，而测试区分别在距固定段4mm处和14mm处。为了解决这一缺陷，更直接地探究材料断裂处的疲劳状态，实验选取带孔的试样，以便在振动过程中形成应力集中。图11展示了带孔样品直到断裂时相位偏移角（SD）随着振动周期数（N）的趋势。

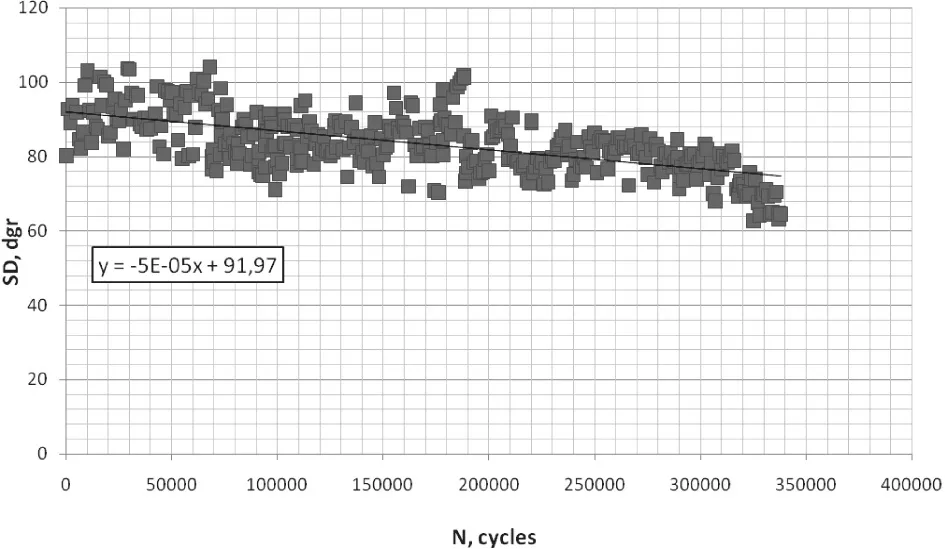
图11 带孔试样相位偏移角与振动周期数的关系

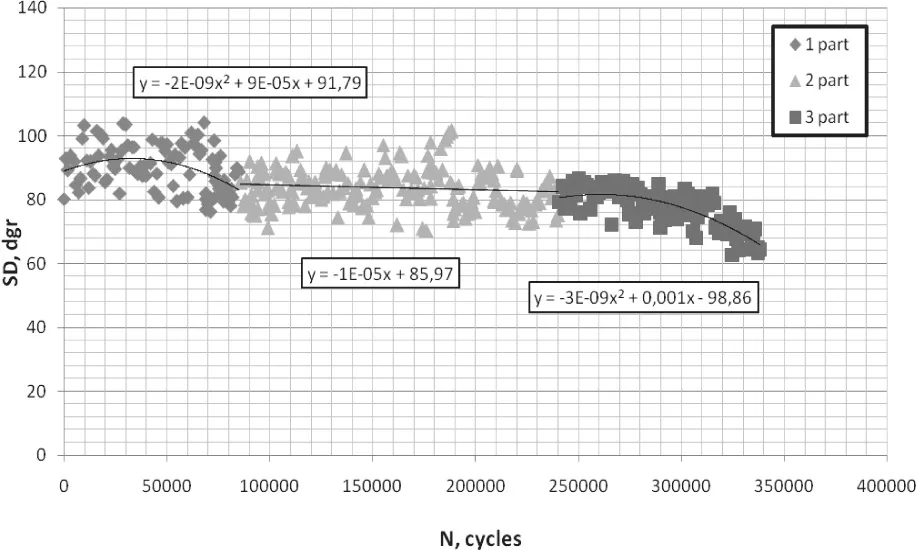
图12 带孔试样相位偏移角与振动周期数的三级关系

趋势线线性方程为：

相位偏移角随着振动周期数的增加呈现下降趋势。

为了更深入地分析两者之间的关系，趋势图可以被分成三部分来研究[6-8]，如图12所示。

第一部分：试样处于振动的初期，相位偏移角随着振动周期数的增加呈现多项式关系，方程如下：

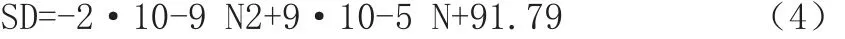
第二部分：随着振动周期数的增加，相位偏移角呈现轻微线性下降趋势，方程如下：

第三部分：此时材料处于疲劳寿命的最后阶段，随着振动周期数的增加，相位偏移角急剧下降，呈现多项式关系，方程如下：

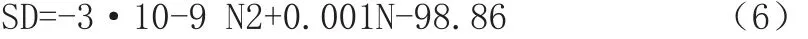
裂纹在此部分产生，此区域可用来估计材料失效前的状态。

4 结论

疲劳实验以弯曲悬臂梁的方式进行。测试机上样品每次振动的振幅恒定，振动频率为25Hz。样品测试区承受预设定的应力载荷。钢12H18N10T为主要的测试材料，对无孔样品的测试能探究不同应力区的疲劳状态，而对带孔试样的测试能直观地展示材料断裂处的疲劳寿命情况。两者都有各自的优缺点。

为了研究频率共振法对无孔样品不同应力区测试的相似性，选取了一些能表征整体趋势的特殊点，比较其处于该趋势位置时振动周期数的关系。比较结果显示不同应力区的测试具有相似性，在一定的振动周期下，共振法在两种应力状态下表征的试样疲劳损伤情况具有相似趋势，证明了共振法对于研究疲劳状态下材料结构微变的科学性。

对带孔样品的研究直观地展示了共振法对于材料断裂处的疲劳损伤探究情况。相位偏移角随着振动周期的增加整体呈现下降趋势。将趋势线分成三个阶段进行分析后可发现当试样趋于断裂时相位偏移角急剧下降。尽管前人已经研究出了多种计算疲劳状态下材料损伤的模型，但是迄今仍没有一种方法能普遍性的被接受，每种模型都存在局限性，只能表征一个或几个单独的现象。频率共振法利用材料具备自振频率这一特性，引入一定频率的信号与试样产生共振，通过对不同振动周期数下相位偏移角的比较来研究疲劳状态下试样物理-机械性能的变化，具有一定的可行性，在工程应用上具备不错的研究前景。

[1]刘建伟.疲劳累积损伤理论发展概述[J].山西建筑,2008,34(23):76-78.

[2]曹定国.美国空军飞机老龄问题及其对策[J].飞机设计参考资料, 2005(4):20-25.

[3]V.E. PANIN Overview on meso-mechanics of plastic deformation and fracture of solids / Theoretical and Applied Fracture Mechanics 30 (1998) P. 1-11

[4]Radchenko A.I. Yutskevych S.S., Panteleev V.M. Synergetic Discretely-Likelihood Fatigue Model Based Structure Lifetime Prediction Methods Improvement: materials of 19th European Conference on Fracture «Fracture Mechanics for Durability, Reliability and Safety» (26 -31 August,2012). – Kazan,2012 – P. 148-154.

[5]Radchenko A.I. Yutskevych S.S.,Panteleev V.M. Aspects of metal fatigue process under two-block loading tests/Aviation in the XXI-st century. Safety in Aviation and Space Technologies: the V world congress, 25–27 Septem¬ber 2012: abstracts. – K., 2012. – P. 1.2.15–1.2.19.

[6] Y. Wang, E.I. Meletis, H. Huang Quantitative study of surface roughness evolution during low-cycle fatigue of 316L stainless steel using Scanning Whitelight Interferometric (SWLI) Microscopy.

[7]Antti Jarvenpaa, L. Pentti Karjalainen, Matias Jaskari Effect of grain size on fatigue behavior of Type 301LN stainless steel.

[8]J.J. Roa, G.Fargas, E.Jiménez-Piqué , A.Mateo Deformation mechanisms induced under highcycle fatigue tests in ametastable austenitic stainless steel.