基于模糊化SEC综合指标体系的电网规划经济性评估方法

鄢晶，杨东俊，郑旭，柴继勇，王莉琳，张世荣

（1.国网湖北省电力公司经济技术研究院，湖北武汉 430077；2.武汉大学动力与机械学院，湖北武汉 430077）

输电网规划是保障电力系统安全稳定运行的重要组成成分。它是根据电力系统负荷及电源发展规划对输电系统的主网架做出的发展规划。电网规划是建设坚强、稳定、高效和持续发展电网的重要保障，同时又是一个涉及多约束条件、非线性、多目标优化的理论性和实践性都很强的工作，因此电网规划一直是各级电网公司和电力专家十分关注的重要工作和研究课题。

目前对电网规划的研究方法很多，各有侧重点且存在一定的不足，传统的投入产出法[1-2]和成本效益分析法[3]关注电网投资的一次成本和局部效益，但对电网投资的长期性和资金的时间因素缺乏考虑；基于全寿命周期成本（lifecycle cost，LCC）理论[4-7]的资产管理分析虽然对设备的整个寿命周期进行了全面的分析，但主要集中在一些特定的设备，建立的模型也比较简单；文献[8]建立了一个针对电力系统整体的三维全寿命周期成本模型，提出了基于全寿命周期成本的电力系统经济性评估方法，将全寿命周期成本理论的运用扩大到整个电力系统，但是没有考虑到安全指标问题。

针对上述问题，本文在全寿命周期成本理论的基础上引入安全指标，建立基于SEC综合指标体系的电网规划方案综合决策体系，针对评估模型指标可能存在的不确定性对其进行了模糊化处理，并基于投影技术给出了模糊多属性决策的方法，同时，建立了经济性评估模型，并给出了评估指标。针对各指标量纲不同的情况，对其进行了归一化处理，并构造了综合评价指标来判断方案的优劣。最后，通过两个工程实例验证了本文所提评估模型的有效性。

1 SEC综合指标体系

SEC综合指标体系包括安全指标（S）、效能指标（E）、差异化全寿命周期成本（C）指标3个方面，每个指标又包含若干个二级指标。其实质就是在对电力公司进行全寿命周期管理的基础上，综合的评价和分析资产的安全性能、效益水平和周期成本，有效的促进三者的综合平衡和有机统一，提高资产管理水平，具体的SEC综合指标体系如图1所示。

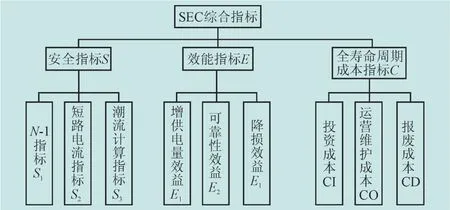
图1 SEC综合指标体系Fig.1 SEC comprehensive index system

1.1 安全指标（S）

安全指标反映规划方案在运行过程中可能存在或遭遇的安全风险性问题。其包括短路电流指标、N-1指标、潮流计算指标。计算公式如下：

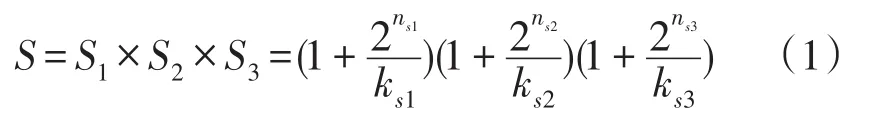
式中：S1、S2、S3分别表示满足N-1不造成一般及以上事故，满足潮流计算、短路计算校验的安全因子，ns1、ns2、ns3分别表示不满足 3 种判据的次数，ks1、ks2、ks3分别表示3种判据的调节系数。

1.2 效能指标（E）

效能指标包括增供电量效益、可靠性效益、降损效益。

增供电量效益是因为供电企业供电能力的加强而引起的售电量的增加值，可以利用增加的售电量收益对投资进行偿还。计算公式如下：

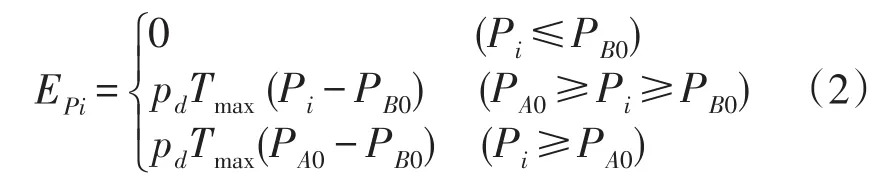
式中：Pi为第i年的最大负荷；PB0为项目投运前选定范围内电网的最大供电能力；Tmax为最大负荷利用小时数；PA0为项目投运后选定范围内电网的最大供电能力；pd为购销差价

可靠性效益是加强电网结构后，因故障而损失的故障值变小而产生的相对收益。计算公式如下：

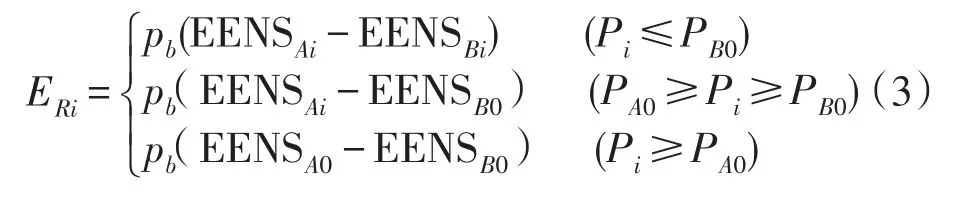
式中：EENS为电量不足期望值；EENSAi为项目投产后第i年的EENS；EENSBi为项目投产前第i年的EENS；EENSB0为项目投产前最大供电能力下的EENS；EENSA0为项目投产后最大供电能力下的EENS；pb为购电价。

降损效益是加强电网结构后，电网的损耗值发生变化而产生的相对收益。由于供电负荷增大，所以降损效益往往是负值。计算公式如下：

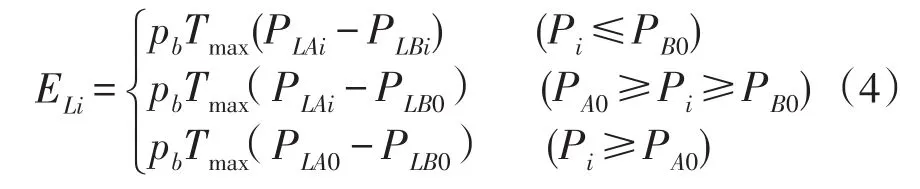
式中：PLAi为第i年的网损值；PLBi为项目投产前选定范围内电网的第i年网损值；PLB0为项目投产前选定范围内电网的最大供电能力下的网损值；PLA0为项目投产后选定范围内电网的最大供电能力下的网损值。

1.3 全寿命周期成本指标（C）

全寿命周期成本（LCC）就是在产品的寿命周期或预期的有效寿命周期内，由产品的投资、设计、使用、检修维护和故障时可能引起的所有费用的总和[9]。其主要思想是通过对设备或系统的LCC进行分析和计算，然后根据量化值进行决策。

1.3.1 初始投资成本（CI）

初始投资成本就是指在电网项目的建设、改造和调试时，由电网项目在正式投运前所产生的一次性费用。

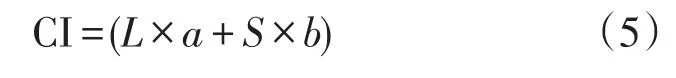
式中：L为线路长度；a为线路单位造价；S为变电站容量；b为变电站单位容量造价

1.3.2 运营维护成本（CO）

运营维护成本主要由设备层运营维护成本和系统层运营维护成本两大部分组成。设备层运营维护成本主要是由检修维护成本、工资相关的额外费用和其它运营成本3部分组成；系统层运营维护成本主要是由停电所引起的成本损失和运营期内所支付的网损成本两部分组成。可以表示为

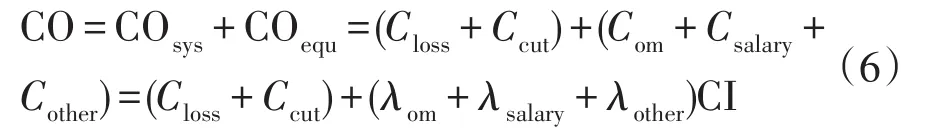
式 中 ：CO、COsys、COequ、COloss、COcut、COo&m、COsalary、COother分别表示总的运营维护成本、系统层运营维护成本、系统层运营维护成本、网损成本、停电成本、检修运维成本、工资成本和其他成本。为了便于计算，设备层运营维护成本中的检修维护成本、工资相关的额外费用和其他运营成本可以根据各自在初始投资成本CI中所占的比例进行计算，其中，λo&m，λsalary，λother分别为 3 项成本在 CI中所占的比例。

1.3.3 报废处置成本（CD）

报废处置成本就是在项目的基建和技改等资本投入时所产生的固定资产在项目报废处置时做引起的各种费用，用下式来表示：

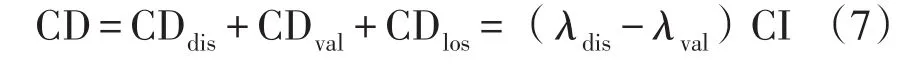
式中：CDdis表示报废处置管理费用；CDval表示报废资产残值回收收入；CDlos表示资产未使用到期望寿命导致的提前报废价值损失；λdis、λval分别表示两项成本所占比例。

2 SEC指标模糊化

在SEC综合指标模型中，全寿命周期成本LCC、安全指标S和效能指标E中含有不确定较强的因素，故需对其进行模糊化处理，方法见参考文献[10-13]。

2.1 安全指标S的模糊化

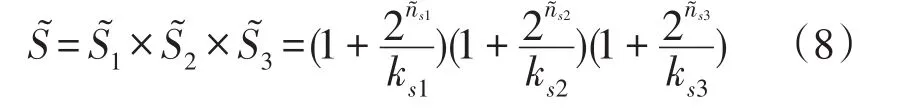
安全指标S模型中，不满足3种判据的次数具有不确定性，故均应考虑其模糊性。

2.2 效能指标E的模糊化

效能指标中的网损和电量不足期望值具有不确定性，需对其模糊化处理。

对由n个节点组成的电网，在网络输入量为确定值的情况下，其总的有功功率损耗为

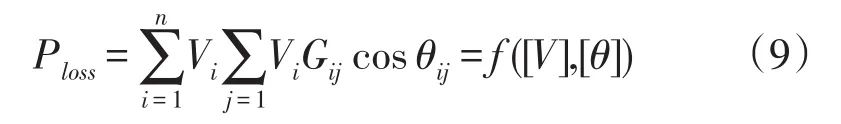
利用Taylor级数将式（19）在对应模糊注入功率中心值的运行点d附近进行展开，略去高于二阶的项并考虑[Δθ]的模糊性（忽略电压幅值变化的影响），则有

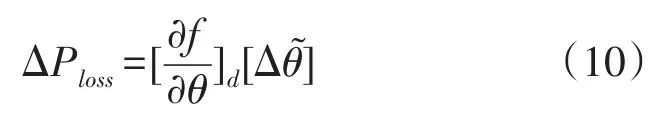
有功模糊网损为

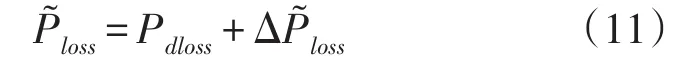
模糊电量不足期望值可由式（22）表示[13]：

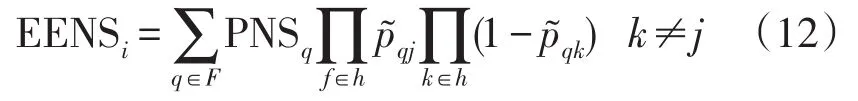
式中:F为导致电网供电不足或中断的所有故障状态集合；h为所有故障设备的集合；H为所有正常设备的集合；及分别为电网在第q种故障状态下第j台和第k台设备故障停运的模糊概率；PNSq为电网在第q种故障状态下向节点i上用户少供的模糊有功功率（即节点i上的模糊缺负荷量），可以通过求解一个模糊线性规划模型得到，其具体计算方法见文献[14]。

2.3 LCC的模糊化

模型中初始投资成本、运维成本具有较强的不确定性，故需针对这些变量的不确定性建立其模糊化模型，进而建立模糊化的LCC计算模型[15]。

2.3.1 初始投资成本模糊化

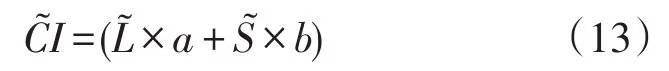
2.3.2 运营维护成本模糊化

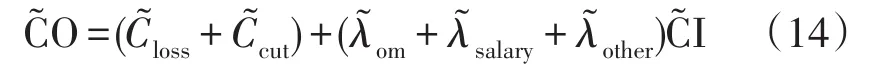
2.3.3 报废处置成本模糊化

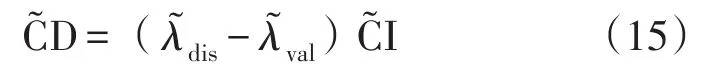
报废处置成本的计算与运营维护成本的计算

类似，其报废处置管理费用和报废资产残值回收收入也是按各自在初始投资成本中所占的比例系数来进行计算，比例系数和也都存在一定的模糊性。

3 SEC综合指标体系评估方法

3.1 经济性评估模型

设定使用年限为第k年，k=1，2，…，N，N为期望寿命周期，考虑资金的时间价值，将成本和效益均折算至现值进行比较[16]。在全寿命周期内的第k年，其差异化累计成本和效益可以表示为

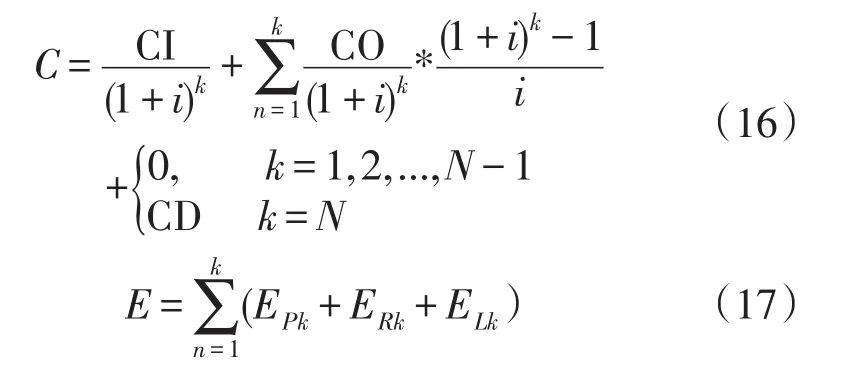
式中，i为折现率。

基于SEC规划比选理念以及经济性评估模型，用研究寿命周期内的总累计加强成本C、期望净收益D（W）和收益成本比SEC来衡量差异化规划方案的经济性，其中，C反映规划方案可能需要的总资本投入；D（W）用于衡量差异化规划方案能否回收成本。

3.2 基于投影技术的模糊多属性决策

针对SEC综合指标体系多属性的特性，层次分析法[17-19]能有效确定各属性的权重，将半定性问题转换为半定量问题。而基于投影技术的模糊多属性决策是针对层次分析法的一种解法，当模糊属性指标或权重值的隶属度为非线性时，该方法具有简单易用的方法。

我们构造方案Ai与正、负理想解的偏差如下:

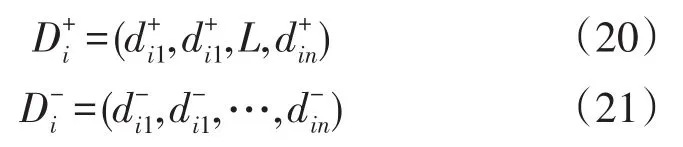
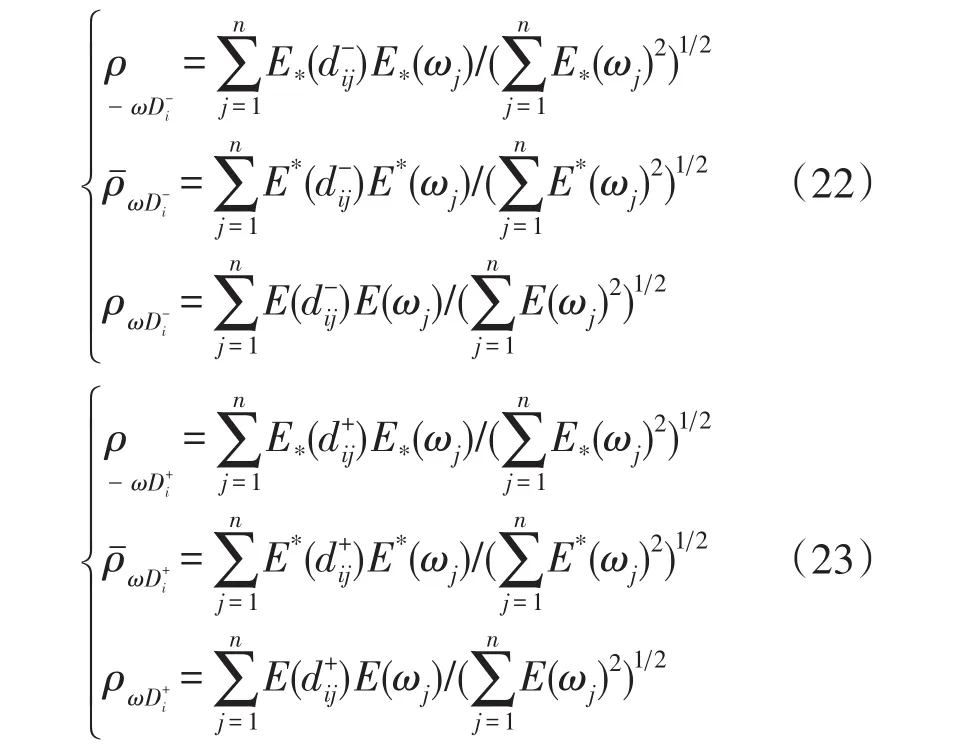
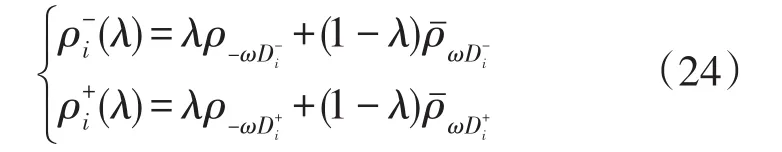
组合投影系数ρi-（λ）是λ的函数，可以解释为方案Ai与负理想解N-的偏差总和。ρi+（λ）可以解释为方案Ai与正理想解P+的偏差总和。PɯDi+，PɯDi-是方案Ai与正、负理想解P+，N-总的期望偏差。很明显，当ρi-（λ），PɯDi-较大时，方案Ai较优:当ρi+（λ），PɯDi+较小时，方案Ai较优。为此，构造衡量方案优劣的函数

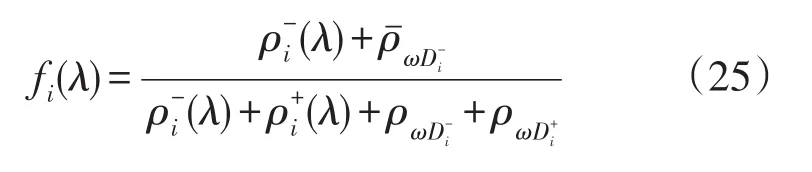
对于给的λϵ[0，1]，fi（λ）越大，方案Ai越优。

3.3 评估指标归一化处理

针对经济性评估和多属性决策指标量纲不同的情况，对其进行归一化处理。

其中，D（W）和fi（λ）为正向指标，即指标越大越好，SEC为反向指标，即指标越小越好，对3项指标进行以下处理：

式中，n为方案数。

经过以上归一化处理后，3项指标均转化为正向指标，最优值为1，最劣值为0。

构造综合评价指标为

λ越大，说明该方案各项指标综合情况越好，反之，则越差。

4 仿真计算

在SEC的成本（C）、效益（E）的各相关分量中，涉及到的主要参数和本案例中的取值如表1和表2所示。

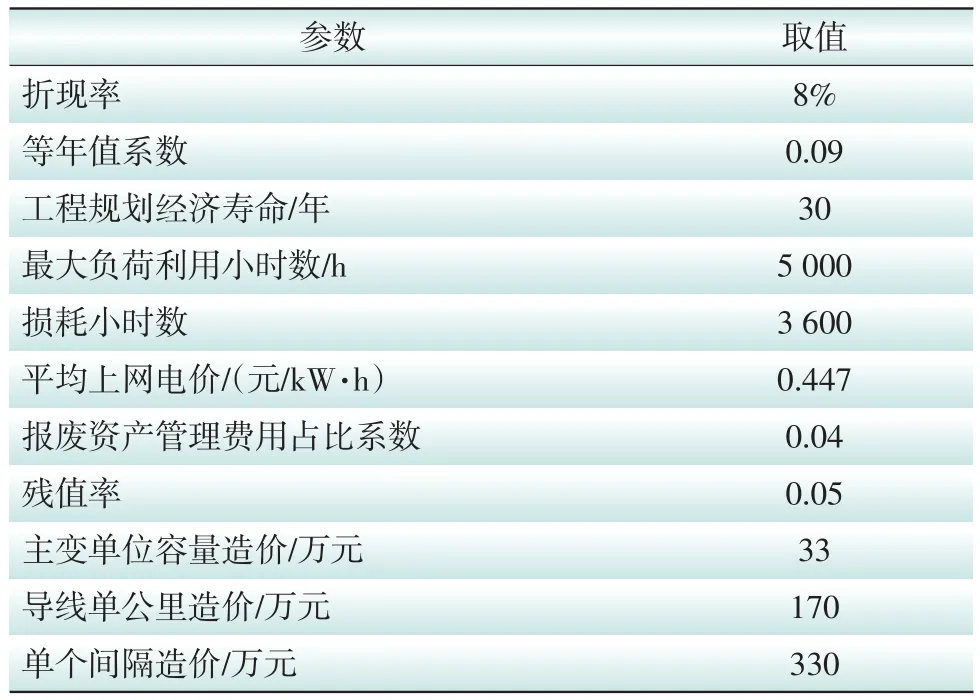
表1 相关参数取值Tab.1 Related parameters

仿真过程中，隶属度函数采用梯形隶属度函数。根据SEC各指标的重要程度，确定判断矩阵为A=[1，1/2，1/3；3，1，3；2，1/3，1]，算得权重w=（0.157 1，0.593 6，0.249 3）T。悲观系数取为 1/3。

4.1 算例1

算例1定义的相关电网选取范围如图2所示。

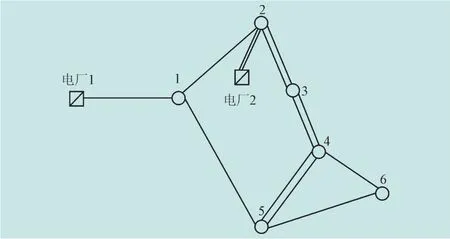
图2 相关电网图Fig.2 Related grid

从原拟定方案中选取的参与SEC比选的方案如下：

方案1：将节点2-节点4两回220 kV线路π入节点3。其中，I回π进线路长约2×0.8 km，导线型号为 LGJ-2×400；II回π进线路长约 2×2 km，导线型号为 LGJ-2×400。

方案2：将节点2-节点4 I回220 kV线路π入节点3，新建线路长约2×0.8 km，导线型号为LGJ-2×400。

仿真结果：经济性评估仿真结果如图3和图4所示，可以看出，当使用年限为20年时，净收益最大，建议使用年限到20年时更新线路。

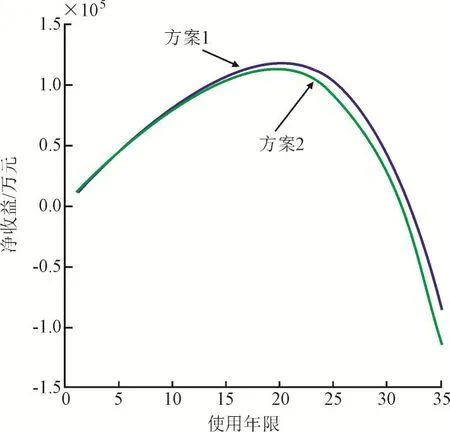
图3 两种方案的净收益比较Fig.3 Comparison of the net benefit between two schemes

当使用年限为20年时，各项指标计算结果如表2所示。

归一化处理后，结果如表3所示。

可以看出，方案1的λ值大于方案2，因此方案1由于方案2。

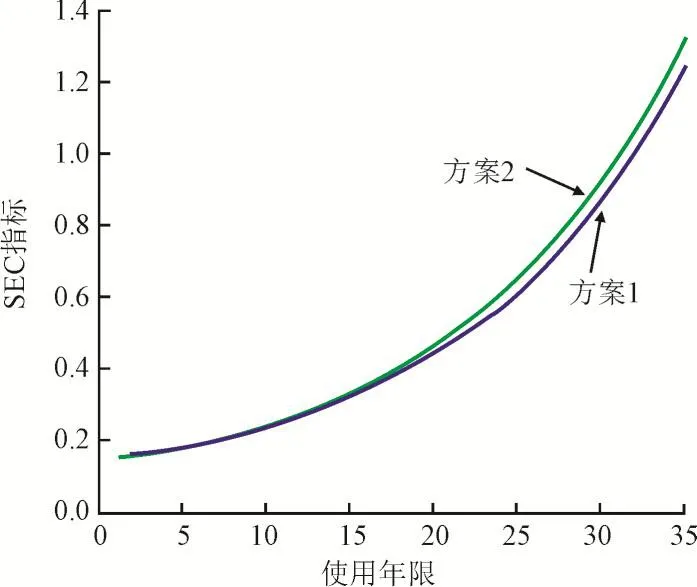
图4 两种方案的SEC指标比较Fig.4 Comparison of SEC index between two schemes

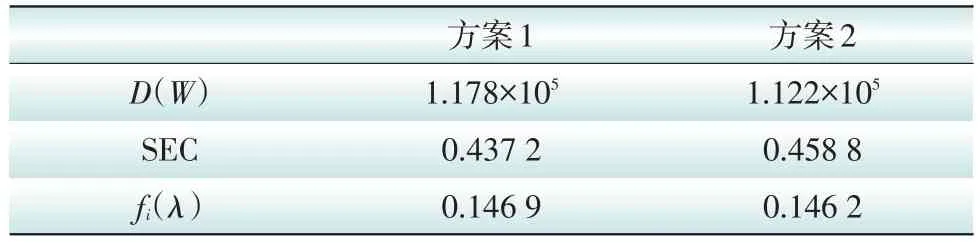
表2 各项指标计算结果Tab.2 Indicators of the results of the calculation

表3 归一化指标计算结果Tab.3 Normalized indicator calculation results

4.2 算例2

算例2定义的相关电网选取范围如图5所示。

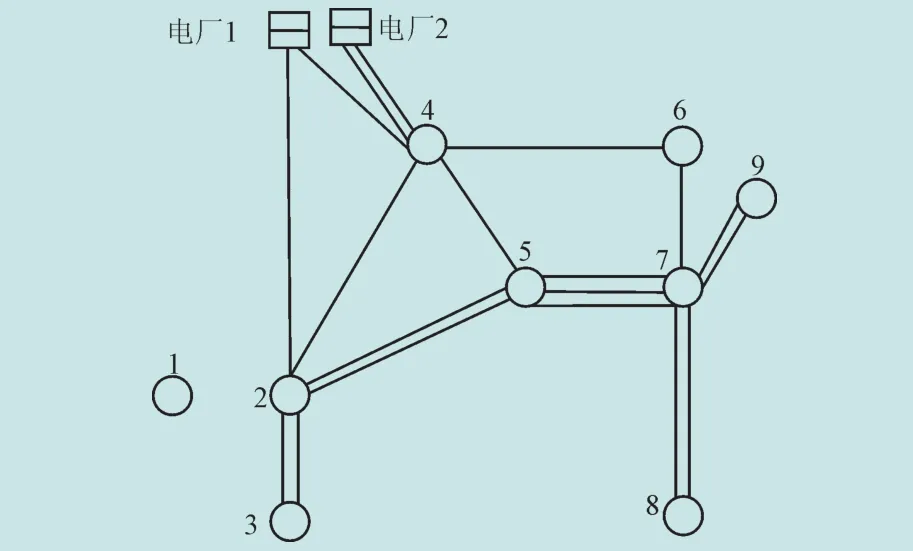
图5 相关电网图Fig.5 Related grid

从原拟定方案中选取的参与SEC比选的方案如下：

方案A2：将节点2-节点5双回改接至节点1，线路长度2×9.0 km，电缆截面为1 000 mm2，钢桂Ⅳ回延伸至和平，线路长度5.0 km，电缆截面为2 000 mm2；

方案B1：将节点4至节点2线路π入节点1，线路长度2×9.0 km，电缆截面为2 000 mm2；

方案B3：将将节点2-节点5Ⅰ回π入节点1，线路长度2×9.0 km，电缆截面为2 000 mm2；

仿真结果：经济性评估仿真结果如图6和图7所示，由于方案B1、方案B3各项收益和成本几乎相同，导致方案B1、方案B3净收益和SEC指标曲线重合。从图可以看出，方案A2的SEC值时刻小于方案B1和B3。同时，使用年限小于25年时，3个方案净收益差别不大，使用年限大于25年后，方案A2净收益明显高于方案B1和B3。

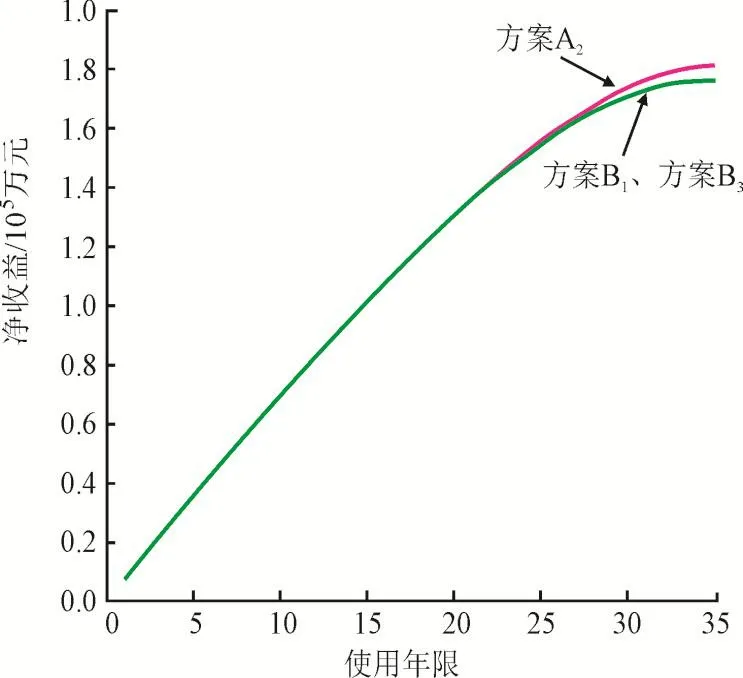
图6 3种净收益比较Fig.6 Comparison of the net benefit among three schemes

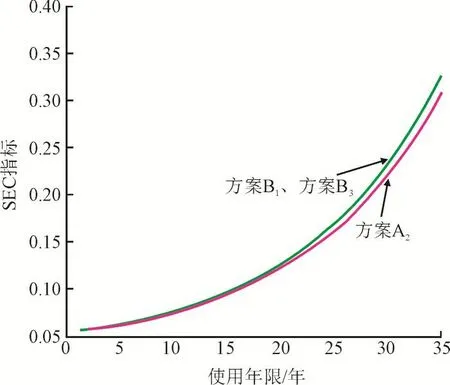
图7 两种方案的SEC指标比较Fig.7 Comparison of SEC index between two schemes

当使用年限为35年时，各项指标计算结果如表4所示。

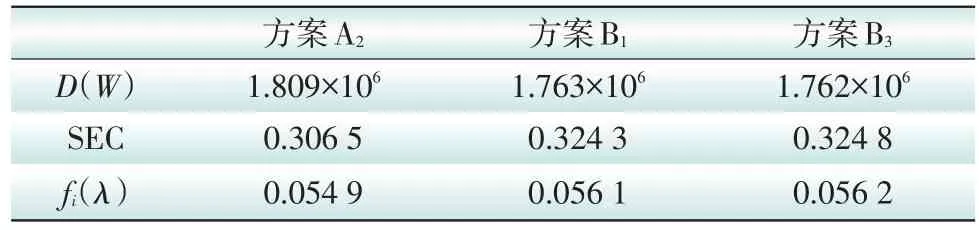
表4 各项指标计算结果Tab.4 Indicators of the results of the calculation

归一化处理后，结果如表5所示。

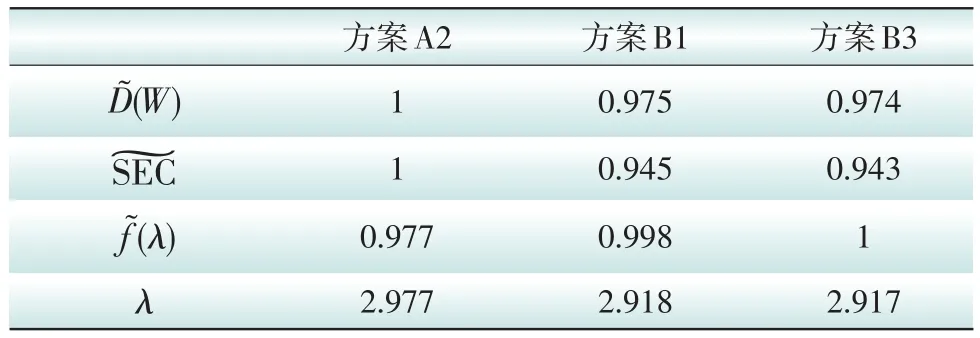
表5 归一化指标计算结果Tab.5 Normalized indicator calculation results

可以看出，方案A2的λ值最大，因方案A2最优。

5 结语

在LCC的基础上，本文引入了安全指标，建立了SEC综合指标体系，并基于投影技术给出了模糊多选择决策的方法，同时，建立了经济性评估模型，从经济性的角度评估电网规划方案。

算例表明，SEC综合指标体系可以反映电网安全和效益综合属性，能够找出最优使用年限。根据基于投影技术的模糊多选择决策方法和经济性评估模型构造的综合评价指标可以选出最优方案，并保证评选结果的合理性。

[1] 何永秀，黄文杰，谭忠富，等.基于投入-产出法的电力失负荷价值研究[J].电网技术，2006，30（1）：44-49.HE Yongxiu，HUANG Wenjie，TAN Zhongfu，et al.Study on value of lost load based on input-output method[J].Power System Technology，2006，30（1）：44-49.

[2] 刘起运，陈璋，苏汝劼.投入产出分析[M].北京：中国人民大学出版社，2006.

[3] 张焰.电网规划中的可靠性成本-效益分析研究[J].电力系统自动化，1999，23（15）：33-36.ZHANG Yan.Research on costbenefit analysis of electric power network reliability planning[J].Automation of Elec⁃tric Power Systems，1999，23（15）：33-36.

[4] ASIEDU Y.Product life cycle cost analysis:state of the art⁃review[J].International Journal of Production Research，1998，36（4）:883-908.

[5] GREENE L E，SHAW B L.The steps for successful life cyclecost analysis[C]//Proceedings of the IEEE 1990 National Aerospace and Electronics Conference，May 21-25，1990，Dayton，OH，USA:1209-1216.

[6] SOLOMON R，SANBORN P A，PECHT MG.Electronic part life cycle concepts and obsolescence forecasting[J].IEEE Trans on Components and Packaging Technologies，2000，23（4）:707-717.

[7] 周喜军，黄华炜，戈京，等.抽水蓄能电站运行方式的LCC 研究[J].华东电力，2006，34（7）：67-70.ZHOU Xijun，HUANG Huawei，GE Jing，et al.LCC research of operation modes for pumped storage power stations[J].East China Electric Power，2006，34（7）：67-70.

[8] 柳璐，王和杰，程浩忠，等.基于全寿命周期成本的电力系统经济性评估方法[J].电力系统自动化，2012，36（15）：45-50.LIU Lu，WANG Hejie，CHENG Haozhong，et al.Economic evaluation of power systems based on life cycle cost[J].Automation of Electric Power Sys-tems，2012，36（15）：45-50.

[9]高教银.建设项目全寿命周期成本理论及应用研究[D].上海：同济大学，2008.

[10]杨纶标，高英仪.模糊数学原理及应用［M］.广州：华南理工大学出版社，2005.

[11]BAAS S，KWAKERNAAK H.Rating and ranking of multipleaspect alternatives using fuzzy sets[J].Automatic，1977，（13）:47-58.

[12]SCGNYCJER K J.Fuzzy sets，natural language computa⁃tionsand risk analysis[M].Maryland，EUA:Computer Sci⁃ence Press，1984.

[13]张焰，陈章潮，谈伟.不确定性的电网规划方法研究[J].电网技术，1999，23（3）:15-22.ZHANG Yan，CHEN Zhangchao，TAN Wei.An approach for transmission system planning incorporating uncertain⁃ties[J].Power System Technology 1999，23（3）:15-22.

[14]张焰，陈章潮，李永腾.电网规划中最小模糊缺负荷量计算研究[J].上海交通大学学报，1999，33（4）：492-494.ZHANG Yan，CHEN Zhangchao，LI Yongteng.Approach to minimizing the fuzzy load not supplied in electric power planning[J].Journal of Shanghai Jiaotong University，1999，33（4）：492-494.

[15]李龙，陈光，陶家铜，等.基于模糊数学的电网规划方案LCC 模型不确定性分析[J].华东电力，2012，40（8）:1316-1321.LI Long，CHEN Guang，TAO Jiatong， et al.LCC uncertainty analysis of network planning programs based on fuzzy mathematics[J].East China Electric Power，2012，40（8）:1316-1321.

[16]宋春丽，刘涤尘，吴军，等.基于差异化全寿命周期成本的电网规划经济性评估方法[J].电网技术，2013，37（7）:1851-1855.SONG Chunli，LIU Dichen，WU Jun，et al.An economic assessment of power system planning based on differentiat⁃ed life cycle cost[J].Power System Technology，2013，37（7）:1851-1855.

[17]周黎莎，于新华.基于网络层次分析法的电力客户满意度模糊综合评价[J].电网技术，2009，33（17）：191-197.ZHOU Lisha，YU Xinhua.Fuzzy comprehensive evalua⁃tion of power customer satisfaction based on analytic net⁃work process[J].Power System Technology，2009，33（17）：191-197.

[18]卢志刚，张炜，王新华，等.多目标多层次模糊综合评价在电力企业运营状况评价中的应用[J].电网技术，2002，26（2）：54-57.LUZhigang，ZHANGWei，WANGXinhua，etal.Application of multiobject multilayer fuzzy comprehensive evaluation of economic operation situation of electric power enterprise[J].Power System Technology，2002，26（2）：54-57.

[19]SUN Q，GE X，LIU L，et al.Smart grid multi-attribute network process comprehensive evaluation method and its application[C]//Power and Energy Engineering Conference（APPEEC）2012.Shanghai，China：IEEE，2012：1-5.

[20]兰继斌，徐扬，霍良安，等.模糊层次分析法权重研究[J].系统工程理论与实践，2006，26（9）：107-112.LAN Jibin，XU Yang，HUO Liangan，et al.Research on the priorities of fuzzy analytical hierarchy process[J].Systems Engineering Theory&Practice，2006，26（9）：107-112.