基于齿轮修形的齿轮箱静动特性研究
2018-01-25陈亮亮
陈亮亮
(浙江经贸职业技术学院,浙江 杭州 310018)
大量实践证明,由于轮齿本身的制造误差和装配误差加上受载后的变形,使得沿齿向的载荷分布不均,同时齿轮在啮入和啮出时,由于基节的偏差将不可避免地要产生冲击和噪声。提高齿轮的加工精度是解决上述问题的主要方法,但对加工工艺提出了更高的要求而且成本也相应提高,而合理地采用齿廓、齿向修形可大大改善齿轮的啮合状况,提高安全性和延长使用寿命。轮齿修形主要方法包括齿向修形和齿廓修形,其中齿廓修形被广泛使用,但齿廓修形的参数选取是否合适一直是研究的热点。
1 齿廓修形
齿廓修形就是在齿顶或齿根圆角部分附近将齿轮修薄,使其齿形逐渐偏离渐开线的修整。齿廓修形主要目的是避免产生“顶刃啮合”,同时也是为了减小单对齿、双对齿交替过程中的波动载荷。实践和研究表明,齿轮的动力性能对齿廓修形参数的选取很敏感,既不能太大也不能太小。如果修形量过小不能避免“顶刃啮合”及载荷的突变,如果修形量过大虽然能避免“顶刃啮合”,但重合度减小,可能导致齿轮箱噪声的增加,达不到修形的目的。因而确定合理的齿轮修形参数,对减小齿轮的啮合振动与传动系统的噪声有着至关重要的作用。
目前齿廓修形的方法大致可分为经验公式法、弹性力学法、函数法、微分几何法和有限元法。经验公式法根据经验公式确定修形量的大小;弹性力学法结合弹性力学的理论推导出变形后修形量,从而选定齿廓修形的修形量;函数法则通过建立齿廓分段修形的修形增量函数,求出修形段的曲线方程并确定修形量。

图1 修形曲线齿端截面图
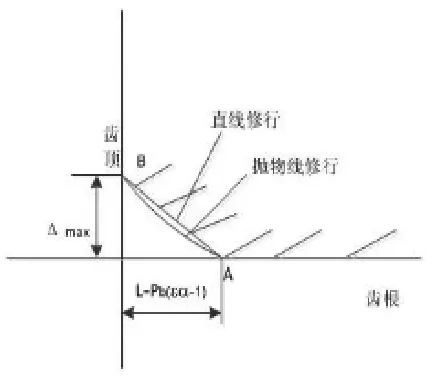
图2 修形曲线展开图
文章综合考虑后采用有限单元法,有限元法则在建立齿轮三维模型的基础上运用有限元软件分析齿轮上的载荷、应力等,再对啮合过程进行仿真分析,从而确定修行量。此方法不仅避免了繁琐的公式计算,还能较准确地得到齿廓修形量。文章研究的对象为低速重载的齿轮箱,图1和图2给出了修形的齿端截面图及展开图。
2 齿轮副静力接触分析
齿轮修形最重要的两个因素是修形方法的选择和修形量大小的确定,要合理地选择修形量,在修形之前就必须进行齿轮副接触分析,掌握齿轮应力的分布及各齿轮的弹性变形量。
文章中研究的齿轮箱其输入额定功率为8800kW,输入额定转速为520r/min,斜齿轮的重合度为2.9948,基于网格的划分和计算时间的考虑,只取部分齿(五对齿)进行分析。采用局部模型来代替整体模型求解,有限元分析模型、最大应力图、单、双齿处位移变形图、齿对间接触压力图如图3、图4、图5、图6所示。
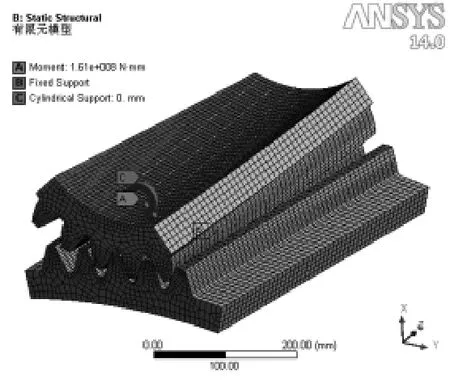
图3 接触分析有限元模型

图4 最大等效应力图

图5 单、双齿交替处位移变形图

图6 齿轮副间接触压力
由上述的分析结果得知:齿轮副之间的等效应力的最大值为704.06MPa,与理论计算值750MPa相接近,表明所建立的几何模型、有限元模型,以及所用假设等的合理性和正确性。理论的计算值偏大是由于在计算赫兹应力时假设的两接触圆柱的宽度为无限长,而实际齿轮副啮合时齿宽是有限的。结合图4获知最大等效应力发生在输出齿轮的齿顶处,此处是齿轮副啮合的啮入点,由于受力面积小且受到较大的冲击,从而出现了应力集中的现象。
图5为单、双齿交替啮合处的弹性变形图,最大变形量很小只有0.0466mm。此处由于受载所产生的变形将会导致齿轮基节发生偏差,从而影响齿轮箱的动力特性。从图6可以看出齿轮副间的最大的接触压力为498.21MPa,且发生处偏于齿轮的一侧,不在齿轮副间,容易发生偏载现象。针对这一情况,可以人为的补偿齿轮的弹性变形(削去齿顶处一部分,即齿廓修形)。
3 齿廓修形静动特性分析
对未修形齿轮的接触静力分析,明确了齿轮啮合时啮合齿之间的相互作用力的大小、分布,以及它们的变形等。发现啮合时存在应力集中及偏载现象,这为后面选择何种修形方式,采用多大的修形量奠定了坚实的基础。
(1)修形前后齿轮的接触应力比较。通过Pro/E在未修形齿轮的基础上分别进行直线和抛物线的齿廓修形,再将修形后的齿轮副模型导入到ANSYS Workbench中进行接触静力分析。有限元单元的选择、网格大小及其划分、约束条件和假设等与未修形齿轮副的分析一致。最后将修形前后分析所得的最大等效应力、接触压力进行对比。
图7、图8为直线修形和抛物线修形的最大等效应力图。图9至10为齿轮副间接触压力图。
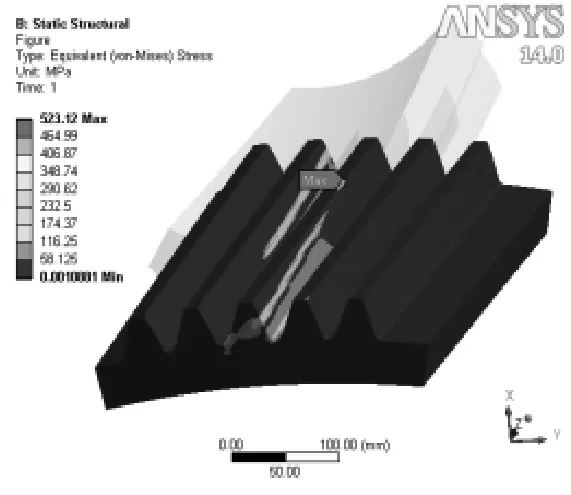
图7 直线修形齿轮最大等效应力

图8 抛物线修形齿轮最大等效应力
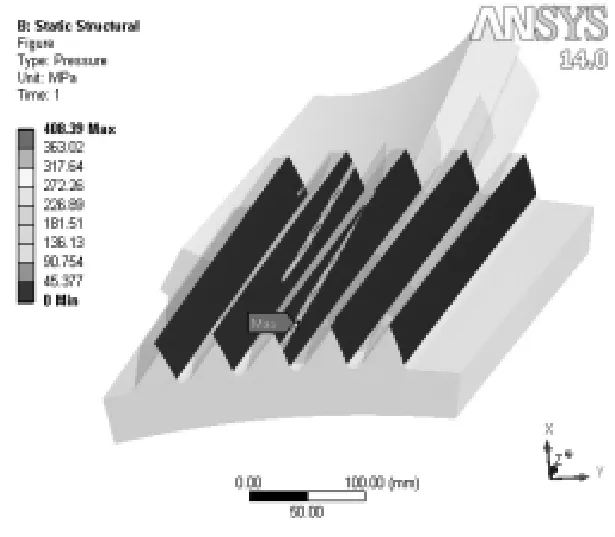
图9 直线修形接触压力分布图

图10 抛物线修形接触压力分布图
从图4、图7和图8分析的结果可知,修形后齿轮副的最大等效应力有所减小,经直线修形后的最大等效应力为523.12MPa,比未修形降低了25.7%,而经抛物线修形后的最大等效应力为315.44MPa,比未修形降低了55.2%之多。通过修形后(削掉“顶刃啮合”部分),最大应力发生位置由齿廓渐开线的顶部向渐开线中部过渡,有效消除了齿顶应力集中现象,修形效果明显,但综合比较发现抛物线修形后从静力学分析的角度上看,优势较为突出。
从接触压力图4、图9和图10可以看到,修形后齿轮的最大接触压力有所减小。经直线修形后的最大接触应力由498.21MPa减小为488.39MPa,但减小的比例不大,而经抛物线修形后的最大接触应力由498.21MPa减小到395.5MPa,与直线修形相比,效果更为明显。在削掉“顶刃啮合”部分后,齿轮副间部分“点——面”接触将改善为“面——面”接触,改善了啮合的工况,使得轮齿在齿轮变形以后仍能保持运转平稳,这样就减少了啮入和啮出的冲击。从图9、图10对比分析可知,最大接触应力由齿轮端面处向齿轮中部过渡,并且齿轮受载变形以后齿面压力分布均匀,变化较为平缓。有效的改善了偏载现象。
(2)修形前后齿轮的接触应力及动力性能比较。以上仅仅从接触静力的变化、等效应力及其分布、轮齿变形等方面分析了未修形齿轮、直线修形和抛物线修形之间的比较。为了更好地阐明三者之间的区别,基于ADAMS对这三种方案进行动力学分析,从动力学角度分析它们对啮合冲击及啮合力等影响。
给主动轮施加520r/min的转速,输出齿轮施加7.3×108N·mm的转矩,齿轮副间施加碰撞接触。选取稳态下的啮合力(0.05s~0.25s),并对啮合力作FFT处理。图11至图13分别给出了三种方案下时域和频域的总啮合力。

图11 未修形齿轮啮合力的时域图和频域图
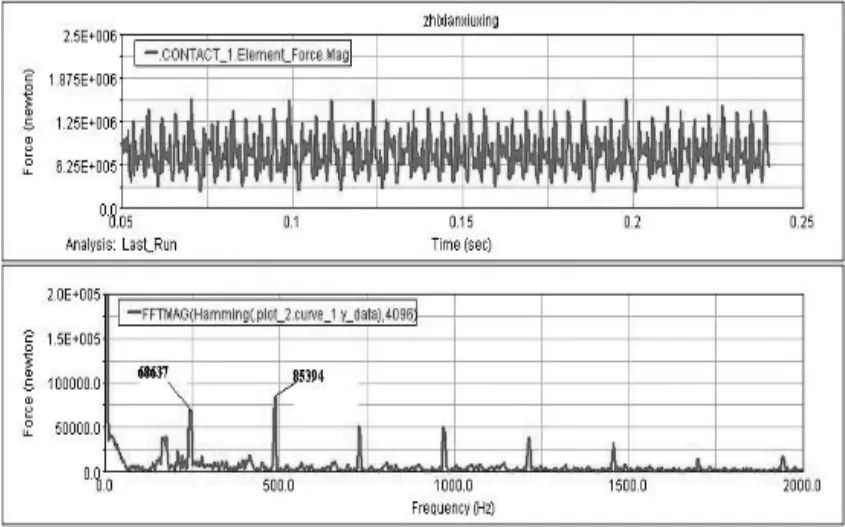
图12 直线修形齿轮啮合力的时域图和频域图

图13 抛物线修形齿轮啮合力的时域图和频域图
从图11可以看出,在修形前齿轮副间的啮合力波动较大,对应的啮合力频域图在一倍频和二倍频处的幅值也较大,则产生振动与噪声的机率较大。图12为直线修形后啮合力时域图和频域图,从图中看出啮合力波动范围减小,且对应的频域图上的一倍频的幅值由359110N降至为68637N,降幅明显,二倍频的幅值由96380N降至85394N,降低了11.4%。图13为抛物线修形后啮合力时域图和频域图,啮合力波动范围同样减小,且对应的频域图上的一倍频的幅值由359110N降至为68980N,二倍频的幅值则由96380N降至64765N,降低了32.8%。
4 结语
通过对修形前后齿轮副间的接触静力、动力特性的分析及比较,得到修形后齿轮副间的应力变化较连续,有效地改善了齿廓“顶刃啮合”现象。同时修形后最大的接触应力趋向齿面的中部,有效地改善了齿面接触受力情况,齿面的受力平稳均匀,同时齿轮间的啮合力波动范围明显减小,振动幅值也明显减小,从侧面说明了修形可以改善啮入和啮出的冲击,对改善齿对间的冲击载荷和振动噪声效果明显。对于直线修形和抛物线修形两种方案,经过接触静力分析和动力学分析后,综合比较得出抛物线修形方案更适合文章研究的齿轮箱系统的减振和降噪。
[1]李润方,王建军.齿轮系统动力学——振动、冲击、噪声[M].北京:科技出版社,1997.
[2]P.velex,J.Bruyere.Some Analytical Results on Transmission Error in Narrow-faced Spur and Helical Gears:Influence of Profile Modifications,Journal of Mechanical Design,2011,(133):1-10.
[3]陆波.基于热弹耦合大功率船用齿轮箱动态性能研究[D].重庆:重庆大学,2009.
[4]刘哲.风电发电机增速器设计与仿真[D].武汉:武汉理工大学,2010.
[5]李润方.齿轮传动的刚度分析和修形方法[M].重庆:重庆大学出版社,1998.
