分数阶永磁同步电机混沌系统的自适应模糊滑模同步控制
2018-01-25任志伟
任志伟
(鹤壁汽车工程职业学院,河南 鹤壁 458000)
现如今,混沌现象不仅是物理界研究的热点,同时也受到了工程技术界的广泛关注,越来越多的技术研究倾向于混沌现象。由于近年来对混沌系统的控制与同步成为控制理论与控制工程领域的重要研究内容,在对控制和同步混沌系统更深刻理解的基础上,许多学者针对各类混沌系统进行了深入研究。然而以上研究大多是基于整数阶混沌系统,近年来在整数阶混沌系统的基础上又出现了分数阶微积分在数值分析混沌系统。分数阶微积分是研究分数阶次的微积分算子特性以及分数阶微分方程的理论,已经有逾300年的历史。随着对分数阶微积分研究的不断深入,研究者普遍认为分数阶微积分作为整数阶微积分的自然推广,极大地扩展了人们所了解的整数阶微积分的描述能力。所以,现今分数阶微积分在数值分析以及物理和工程等不同领域中的应用,越来越多地引起了广泛的关注。分数阶微积分理论在不同领域应用研究的显著增加,同样也引起了控制领域专家和学者们的重视,有关分数阶混沌系统的控制与同步问题研究也日益增多。
近年来,由于智能控制的不断完善和发展,特别是模糊控制的不断发展,分数阶混沌系统的模糊控制也得到了一定的发展,很多学者针对分数阶混沌系统,利用分数阶T-S模糊模型,研究了其控制问题;有些文献针对分数阶区间不确定系统,利用分数阶T-S模型建模,设计了能够镇定系统的状态反馈控制器,并应用到一类带有不确定参数的分数阶混沌系统中。另一方面,滑模变结构控制已经形成了一个相对独立的研究分支,适用于线性与非线性系统、连续与离散系统、确定性与不确定性系统等,并且在实际工程中逐渐得到推广应用。在混沌系统的同步研究中,滑模控制也得到了广泛的应用,有些文献针对一类带有外部扰动的分数阶混沌系统,研究了自适应滑模同步控制问题。更进一步,采用主动滑模控制器,有些文献通过探讨分数阶主从结构混沌系统的同步控制问题。针对带有时滞的分数阶混沌系统,基于自适应模糊滑模控制,但是对于有关分数阶混沌系统的T-S模糊滑模控制,仍有许多亟待解决的问题。
文章在深入分析研究分数阶永磁同步电机混沌系统结构特点的基础上,采用T-S模糊模型对系统进行重构。基于状态反馈和模糊控制思想,研究了分数阶永磁同步电机混沌系统的模糊控制算法。并大胆引入了滑模控制策略,成功设计了能够使分数阶永磁同步电机混沌系统渐近同步的模糊滑模自适应控制器,特别是文章所讨论的系统充分兼顾了实际系统中含有不确定和外部扰动的情况。文章最后利用Matlab-Simulink软件进行了仿真实验,取得了令人满意的结果,从而证实了文章提出的分数阶永磁同步电机混沌系统T-S模糊滑模自适应控制算法的有效性。
1 系统描述
在此章节,考虑如下含均匀气隙的永磁同步电机系统的数学模型

其中,ω、id和iq是状态变量,分别表示角速度,d轴电流和q轴电流。σ和γ是系统的操作参数且为正常数和q分别表示负载转矩,d轴电压和q轴电压。系统(1)中,令外部输入为零,即。其中,当σ和γ的取值在特定范围内时,系统(2)能产生混沌特性,例如σ=5.45,γ=20。这种混沌行为会破坏永磁同步电机系统的稳定性,为了消除或控制混沌现象,可将ud作为一个可调变量,在现实应用中也是可以实现的。接下来,令

可得到

由于系统内部阻尼所引起的动态效果可以通过分数阶微积分来进行描述,根据系统(3),将分数阶永磁同步电机混沌系统作为驱动系统,其数学模型描述如下:

其中,当 σ=5.45,γ=20,α=0.95 时,其混沌吸引子如图 1所示。

图1 加入控制前系统(4)相轨迹
2 系统重构
考虑如下分数阶系统

由T-S模型描述的模糊规则i:如果z1(t)是Fi1且z2(t)是Fi2且…且zn(t)是Fin,则对于系统(4)采用单点模糊化,乘积推理,中心加权平均解模糊,可得到模糊系统的整个状态方程为:
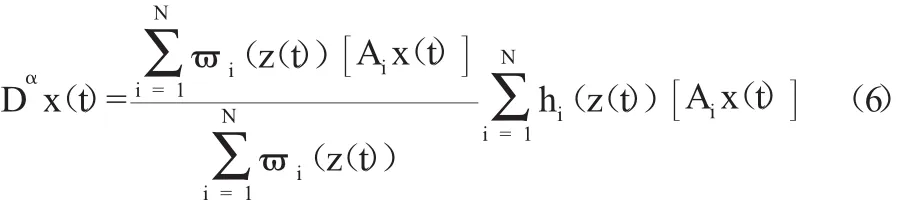
式中:x(t)∈Rn为状态变量;Fij(zj(t))是zj(t)关于模糊集Fij的隶属度函数;Ai∈Rn×n;N表示模糊推理规则数
在分数阶永磁同步电机混沌系统中具有两个非线性项x1x3和x1x2为构造成式(6)的模糊系统,需要将两个非线性项表示成一些线性函数的权重线性和。

式中,g1(x(t))=M1,g2(x(t))=M2,M1和M2为模糊集。因此,针对系统(4),为了得到形如式(6)的模糊系统,可以建立如下模糊规则:
分数阶永磁同步电机混沌系统处于混沌时,假设x1的取值范围是[-20,20],因此取 M1=-20,M2=20。通过 T-S模糊模型重构后的分数阶永磁同步电机混沌系统其吸引子形状与重构之前的吸引子相同。考虑到实际应用中,系统的不确定性和外部扰动都是不可避免的,因此通过重构系统,带有模型不确定和外部扰动的全局模糊系统数学模型可以描述如下:


同理,依照上述模糊规则,将系统(5)按照相同的方式进行系统重构,则重构后的响应系统如下:
其中,Δf(x,t)和Δg(y,t)分别表示系统(4)和(5)的不确定性,dx(t)和 dy(t)分别表示系统(4)和(5)的外部扰动,且满足
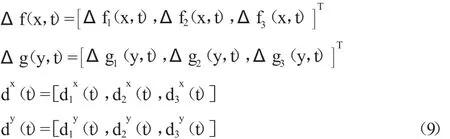
假设1:系统(4)和(5)中的不确定项Δf(x,t),Δg(x,t)是有界的,且满足其中(i=1,2,3)是正实数。
假设 2:系统(4)和(5)中的外部扰动项 dx(t),dy(t)是有界的,且满足,其中ξi(i=1,2,3)是正实数。
定义1:针对分数阶驱动系统(4)和分数阶响应系统(5),如果存在一个控制器ui(t)(i=1,2,3)使得下列等式成立:
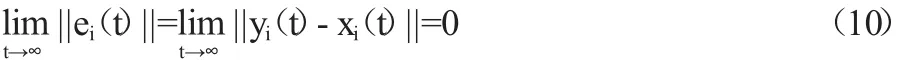
则分数级驱动系统(4)和分数阶系统(5)实现渐近同步。
因此,我们目标就是设计一个能够保证误差系统ei(t)=yi(t)-xi(t)渐近稳定的控制器。
3 模糊滑模自适应控制器设计
在此章节,首先选取如下滑模平面如下:

根据滑模控制方法可知,当系统状态到达滑模平面时,则满足

考虑到现实应用中,系统的不确定和外部扰动是是未知或者不可测得的,因此根据式s·(t)=0,等效控制率ueq可以设计如下:
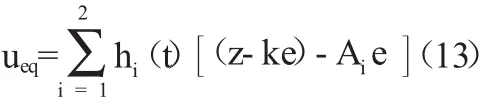
这里,为了保证到达速率,一种新的滑模到达率ur设计如下:

其中为自适应参数且满足 k1,k2,k3,α,β>0 且自适应率

结合式(11)和(12),可将模糊控制器设计如下:

定理1 若存在一个如式(16)的控制器,则系统(4)和(5)可以实现渐近同步。
4 数值仿真
为了验证上述所提控制方法及控制器的有效性,现选取系统的参数如下:

利用上述参数,通过对系统进行数值仿真,可得到如下仿真结果。图2为目标系统(4)和(5)受控后的状态响应x1(t),y1(t),图 3 为滑模平面 s(t)的状态响应。

图2 受控后系统(4)和(5)的状态响应x1(t),y1(t)

图3 滑模平面si(t)(i=1,2,3)
5 结语
文章研究了带有不确定以及外部扰动的分数阶永磁同步电机混沌系统的同步问题,基于T-S模糊模型,首先对分数阶永磁同步电机混沌系统进行了系统重构,给出了重构后的模糊系统数学模型,然后结合滑模控制,自适应控制理论,设计出了能够保证分数阶误差系渐近稳定的模糊滑模自适应控制器。仿真结果表明,文章所设计的控制是有效的。
[1]Zeng H,Park J H,Xiao S.Further results on sampled-data control for master-slave synchronization of chaotic Lur’e systems with time delay[J].Nonlinear Dyn,DOI 10.1007/s11071-015-2199-6.
[2]卢俊国,魏荣,汪小帆,等.连续混沌系统控制与同步的自适应方法[J].控制与决策,2002,17(1):114-116.
[3]GE S S,Wang C.Uncertain chaotic system control via adaptive neural design[J].International Journal of Bifurcation and Chaos,2002,12(5).
[4]刘恒,李生刚,孙业国.带有未知非对称控制增益的不确定分数阶混沌系统自适应模糊同步控制[J].物理学报,2015,64(7).
[5]潘光,魏静.一种分数阶混沌系统同步的自适应滑模控制器设计[J].物理学报,2015,64(4).
