基于模糊C聚类对城市宜居性的综合评价

吴忠诚， 朱家明， 邓卓航

(1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030; 2.安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030)

随着我国经济的快速发展，普通家庭可支配收入越来越多，这一切为追求高品质生活带来可能，宜居城市逐渐成为新时期选择概念.宜居城市的主要影响因素包括人均可支配收入、环境、房价、医疗等，本文试图就城市的适宜居住条件，综合城市的主要指标，给出划分适宜的量化标准来对城市适宜进行综合评价.经查阅诸多文献，发现当前研究文献所采取评价体系在权重的赋值上都带有很强的主观因素，这会导致结果偏向研究者的预先设想，从而降低结果的可靠性.若为了研究结果可靠而通过问卷统计赋权，则会耗用大量的人力物力且会拖长研究的时间，进而影响研究进度.本文就此目的，来挖掘对城市的宜居性产生显著影响的因素指标，并对此进行筛选，找出主成分，建立一套基于影响指标的模糊评价体系，推广并应用到实际.这对于居民综合选择宜居城市给出有效的建议，同时指出了另外城市不宜居的内在原因所在，为提高和完善各城市建设与发展指明方向.

1 数据的选取及假设

本文的数据均来源于各个城市的统计年鉴和统计局官网，为了保证数据的准确定，查阅宿迁、连云港、宿州、商丘、济宁、枣庄、徐州、淮北8个城市2016年的《统计年鉴》和各城市的统计局数据如表1.为了便于解决问题，提出两条假设：所选取的20个初始指标已经覆盖了宜居评价的所有方面；评价指标中各个数据来源准确、有效.

表1八个城市的各评价指标数据

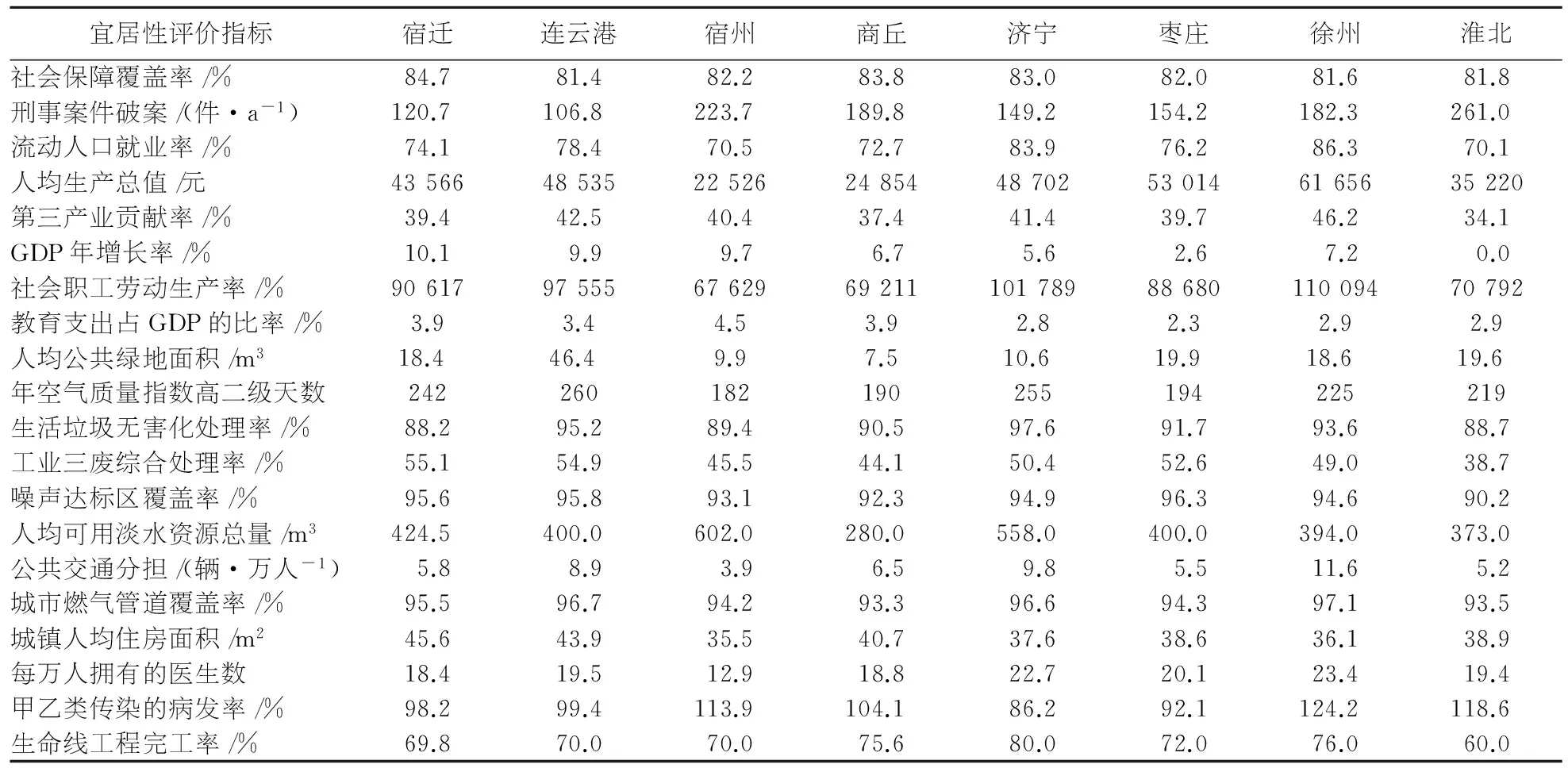
宜居性评价指标宿迁连云港宿州商丘济宁枣庄徐州淮北社会保障覆盖率/%84.781.482.283.883.082.081.681.8刑事案件破案/(件·a-1)120.7106.8223.7189.8149.2154.2182.3261.0流动人口就业率/%74.178.470.572.783.976.286.370.1人均生产总值/元4356648535225262485448702530146165635220第三产业贡献率/%39.442.540.437.441.439.746.234.1GDP年增长率/%10.19.99.76.75.62.67.20.0社会职工劳动生产率/%906179755567629692111017898868011009470792教育支出占GDP的比率/%3.93.44.53.92.82.32.92.9人均公共绿地面积/m318.446.49.97.510.619.918.619.6年空气质量指数高二级天数242260182190255194225219生活垃圾无害化处理率/%88.295.289.490.597.691.793.688.7工业三废综合处理率/%55.154.945.544.150.452.649.038.7噪声达标区覆盖率/%95.695.893.192.394.996.394.690.2人均可用淡水资源总量/m3424.5400.0602.0280.0558.0400.0394.0373.0公共交通分担/(辆·万人-1)5.88.93.96.59.85.511.65.2城市燃气管道覆盖率/%95.596.794.293.396.694.397.193.5城镇人均住房面积/m245.643.935.540.737.638.636.138.9每万人拥有的医生数18.419.512.918.822.720.123.419.4甲乙类传染的病发率/%98.299.4113.9104.186.292.1124.2118.6生命线工程完工率/%69.870.070.075.680.072.076.060.0

注:表1的部分数据的来源无法从《统计年鉴》和统计信息网站上直接获取，需进行相应的转换处理，但数据的有效性可以得到保证.

2 对宜居城市评价指标体系的构建

为了得到较全面地对城市的宜居性做出评价的指标，依据2016年12月最新出台的“宜居城市科学评价标准[1]”，选取社会文明、经济富裕、环境优美、资源承载、生活便宜、公共安全六个方面作为二级指标.这六个方面融合了广大专家和社会公众的智慧，简繁得当、权重合理，可操作性强，达到了较高水平，对于贯彻科学发展观、构建和谐社会，指导全国各城市规划、建设、管理，具有较高的科学指导价值和实用价值.然后再对六个方面二级指标下面仅仅选取易于统计数据和具有代表性的城市宜居评价指标，可构建出宜居性评价指标体系[2]，如图1所示.

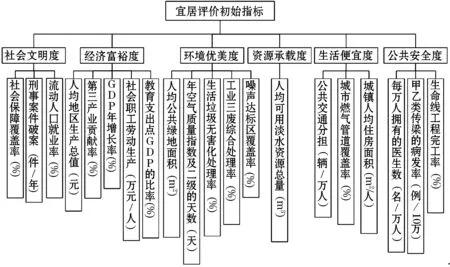
图1 影响城市宜居的评价指标体系

3 主成分分析法提取主成分

3.1 研究思路

针对表1中的八个城市各评价指标数据，考虑到初始选定评级指标中会存在变量数据之间存在较大关联度，可选择用主成分分析法进行相应的指标筛选.对消除量纲后的一致性数据进行因子分析并抽取主成分[3]，最后对主成分的的可靠性进行相关系数检验.

3.2 研究方法

1)截面数据消除量纲

考虑到表1中数据属于统计学中截面数据，而截面数据存在数据非一致性的特性，故先进行数据的标准化.采用min-max标准化，对原始数据进行线性变换.设mina和maxa分别为属性a的最小值和最大值，将a的一个原始值x通过min-max标准化映射成在区间[0,1]中的值x，其公式为：

2)数据的因子分析

对上述消除量纲后的具有一致性的数据进行SPSS降维因子分析[4]，仅仅选取得到对总的数据贡献率为1的前七个宜居性评价指标的总方差解释表2.

表2部分总方差解释表

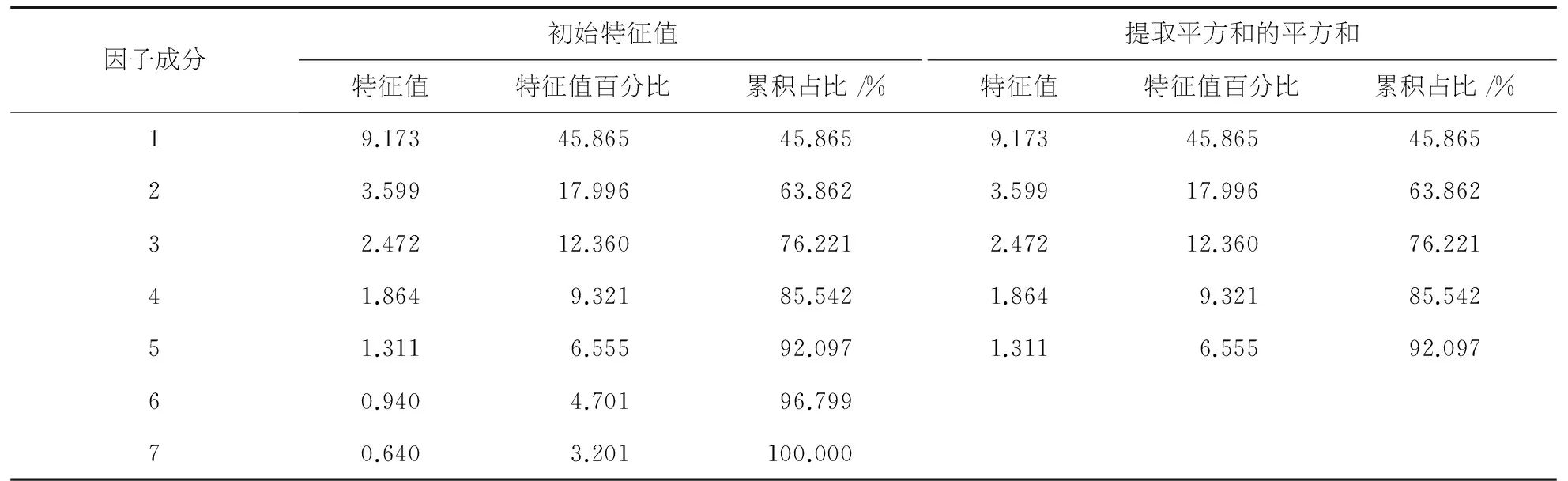
因子成分初始特征值提取平方和的平方和特征值特征值百分比累积占比/%特征值特征值百分比累积占比/%19.17345.86545.8659.17345.86545.86523.59917.99663.8623.59917.99663.86232.47212.36076.2212.47212.36076.22141.8649.32185.5421.8649.32185.54251.3116.55592.0971.3116.55592.09760.9404.70196.79970.6403.201100.000

在表2中，特征值的大小反映了公因子的方差贡献.特征值百分比为特征值占方差的百分数.方差累积占比为特征值占百分数的累加值.抽取平方和载入栏为根据特征值大于1的原则抽取的5个因子的特征值，占方差百分数及其累加值.这5个因子能够较全面的反映92.10%的信息.故可以用这五个因子来代表原研究过程中的20个评级指标，极大地简化了运算的复杂度，为后续的研究提供了方便.

3)主成分提取

为了得到这五个主成分所代表的原数据指标.采用SPPS软件进行因子得分计算，计算结果显示：五种主成分分别是GDP年增长率(%)、社会职工劳动生产(万元/人)、人均公共绿地面积(平方米)、人均可用淡水资源总量(m3)、甲乙类传染的病发率(例/10万).为了后续研究的需要，我们分别对以上五个变量赋予变量符Xi(i=1,2,3,…,5).

4)相关系数检验

从分析的结果可以看出，虽然对于城市宜居性产生影响的指标有很多，但是其中的大部分指标之间都存在一定的相关性，采用主成分提取技术可以将其中五个在显著性的水平下不能相互替代的指标数据提取出来，为了证实所得到的指标之间没有明显的相关关系，采用相关系数分析法进行验证[5]，验证所需的公式为

3.3 结果分析

使用统计软件STATA进行计算相关系数矩阵如下：

相关系数矩阵显示在不考虑其他影响因素的情况之下，以上五个主成分之间存在非常弱的相关关系.即验证了了所得到的五个主成分的相对独立性.

4 对城市在宜居性模糊C均值聚类分析

4.1 研究思路

“宜居性”是一个较为模糊的概念，本文采用模糊评价模型，对上述八个城市建立模糊评价模型，对上述城市在宜居性这一个方面划归为三类，即适宜居住、较适宜居住、较不适宜居住.

4.2 研究方法

1)数据预处理

在进行模糊聚类之前,因为所要进行聚类的数据分为两种类型，即越大越好的数据和越小越好的数据.为了进行合理的标准化，采用如下的量化标准[6].

其中：sij为第j个城市的第i个指标的标准值；cij为评价体系中根据实际查阅资料所得到的第j个城市的第i个指标的实测值；cmin为所对应指标中的最小值乘以1.05；cmax为所对应指标中的最大值乘以1.05；得到标准化后的八个城市的五个指标数据表3.

表3八个城市主要指标数据

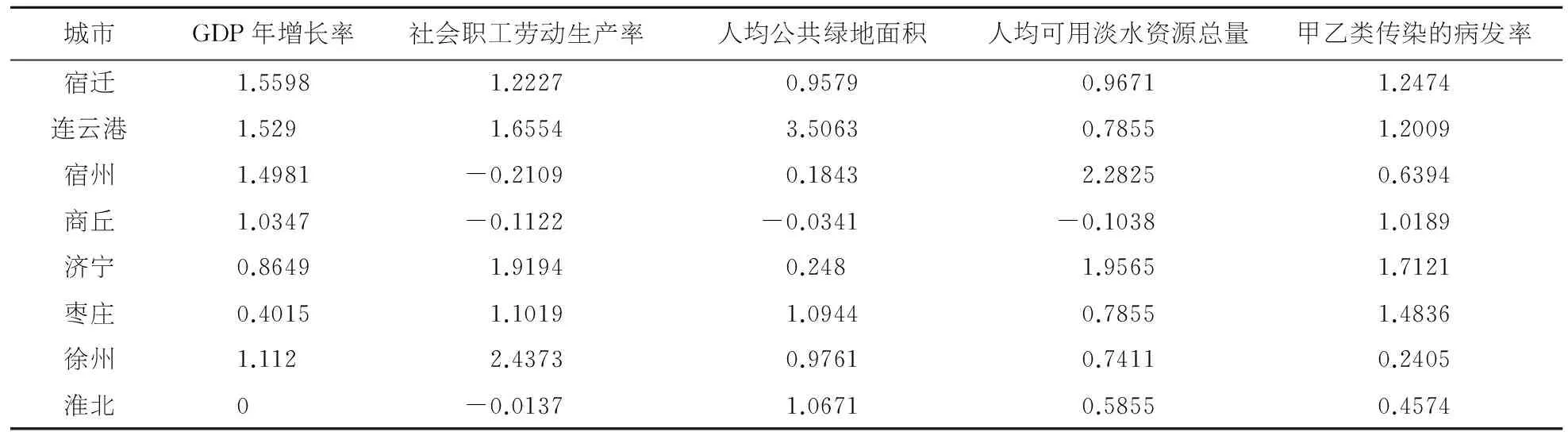
城市GDP年增长率社会职工劳动生产率人均公共绿地面积人均可用淡水资源总量甲乙类传染的病发率宿迁1.55981.22270.95790.96711.2474连云港1.5291.65543.50630.78551.2009宿州1.4981-0.21090.18432.28250.6394商丘1.0347-0.1122-0.0341-0.10381.0189济宁0.86491.91940.2481.95651.7121枣庄0.40151.10191.09440.78551.4836徐州1.1122.43730.97610.74110.2405淮北0-0.01371.06710.58550.4574

2) 进行模糊C均值聚类[7]

把以上八个城市每行五个指标数据作为一个向量xi(i=1,2,…,8)分为3个模糊组(即适宜居住、较适宜居住和较不适宜居住)，并求每组的聚类中心，使得非相似性指标的目标函数达到最小，而每个给定数据点用0～1之间的隶属度来确定其属于各个组的程度.

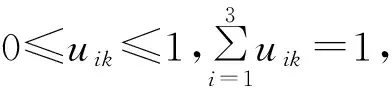
其中：dik=‖xk-vi‖表示第k个序列到第i类中心的欧几里得距离.

由拉格朗日乘数法构造新的辅助函数：

当Y(X,v1,v2,v3)取得最小值的必要条件是：

和

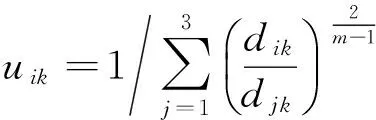
因上述两个必要条件的存在，模糊C均值聚类算法就可以看成如下迭代过程：

①取定c,m和初始隶属度矩阵U0,迭代步数I=0；

②计算聚类中心V为：

③修正的U：

4.3 结果分析

在Matlab软件中调用fcm函数进行编写程序，求解最终对上述的8个城市的样本的分类结果如表4所示. 表4中聚类的结果表示：在所要进行分析的八个城市中，宿迁、济宁、枣庄和徐州表现出了较好的宜居性，城市连云港相对于上面四个城市而言，其宜居性稍差一些，而宿州、商丘和淮北这三个城市在此次聚类中相比较而言的宜居性最差.为了检验模糊C均值聚类结果的准确性，对上述模糊C均值聚类的有效性进Friedman检验.

表4各个城市宜居程度聚类

类别适宜居住较适宜居住较不适宜居住城市名称宿迁济宁枣庄徐州连云港宿州商丘淮北

4.4 聚类结果的Friedman检验

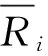
的周围，统计量

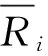
Q≥c

其中:临界值c由PH0{Q≥c}=α确定，此检验称为Friedman检验[8].

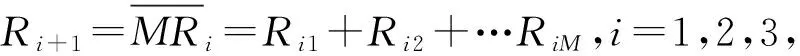
对于检验水平α=0.05，使用软件Matlab编程后采取各类别之间检验，分别得到所分的三类样本数据之间的的非参数检验P值如表5.

表5各类别之间的Friedman检验P值

宜居类别适宜居住较适宜居住不适宜居住类别样本间非参P值0.35921.00000.4021

显然，各类别之间的检验全部接受原假设，即分类后的各个城市样本之间的差异性很小，可以分为一类.符合聚类的基本原则.

5 结 语

本文就现代城市的宜居性做出了一套完整的评价方案.尽管模型的主成分分析和模糊C均值聚类的结果每一步都进行检验，但是作为对于现代城市的各项数据之间的复杂关系，仅仅用这一种方法是稍有片面的，不能较完整的分析出正确的结论.对于整个模型来说，最大的特点是将城市的一个较为模糊的宜居概念，通过数据的处理转化、分析数据所能承载的最大信息并对城市做出一个合理的评价.但是因考虑到研究内容的简洁性，本文所选取的评价指标只是所有指标中较小的一部分，这也决定了最终模糊分类会存在一定的误差，但这并不影响整个模型的评价效用，后续的研究只需在此论文的基础上再做调整即可.对于这种模糊概念量化综合评价模型，不仅仅可以评价城市的宜居度，还可以推广到城市的教育水平、卫生情况等领域.具有较高的研究和发展价值.

[1] 中国城市科学研究会.宜居城市科学评价标准[R].中华人民共和国建设部科技司:中华人民共和国建设部科技司, 2007.

[2] 全少莉,刘养洁.我国主要城市的宜居性评价[J].山西师范大学学报:自然科学版,2010,24(2):112-116.

[3] 朱晓峰.主成分分析与因子分析在体育科研中的应用研究[D].芜湖:安徽师范大学,2006.

[4] 李 欣,张明明.SPPS22.0统计分析[M]. 北京:电子工业出版社, 2015.

[5] 朱存斌,朱家明,陈岩.葡萄酒质量的评价与分析[J]. 佳木斯大学学报:自然科学版,2013,31(3):419-424.

[6] 李丽萍,吴祥裕.宜居城市评价指标体系研究[J].中共济南市委党校学报，2017(1): 16-21.

[7] 杨桂元.数学建模[M]. 上海:上海财经大学出版社, 2015.

[8] 王炯滔,金 明,李有明,等.基于Friedman检验的非参数协作频谱感知方法[J].电子与信息学报,2014(1): 61-66.