水轮机调速器PID调节规律研究

2018-01-25胡千佳罗庆跃邹长春

建材与装饰 2018年3期

关键词：调速器水轮机调节

胡千佳罗庆跃邹长春

（邵阳学院湖南邵阳 422000）

1 引言

在水轮机运行过程中，数字PID可对机组转速进行调节，与传统的机调和电调相比维护难度较小，同时可实现综合自动化控制，应用优势明显。因此，对水轮机调速器PID调节规律进行详细探究具有重要的现实意义。

2 水轮机调节的任务和特点

水轮机调速器是由多个元件组成的，包括测量、放大、执行元件等，其调节对象为水轮机、发电机、引水系统等。在调速器PID的实际应用中，水轮机发电机组首先将转速信号传递至需被测量的元件上，然后对元件的频率信号进行测量，将其转化为电压信号，最后将该信号传递与给定信号进行比较，确定频率偏差实际情况，并就此进行调节。调节指令被放大后，即可传送至执行机构中，推动导水机构，与此同时，反馈元件还可将导叶开度的变化情况传递至加法器中。水轮机调节系统结构形式如图1所示。

图1 水轮机调节系统方块图

3 水轮机调节系统PID控制原理

在水轮机运行过程中，调速器PID是一种常见控制方式，常规PID控制系统原理如图2所示。

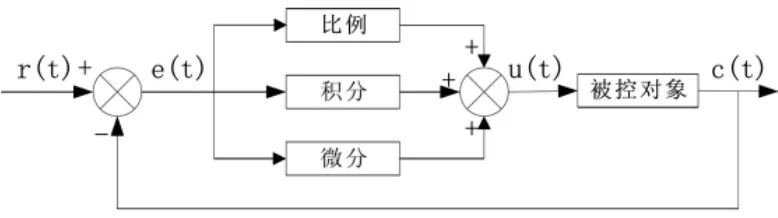
图2 PID控制系统原理框图

PID控制器是一种线性控制器，根据给定值r（t）以及实际输c（t），即可确定偏差：

对于偏差比例（P）、积分（I）以及微分（D），可以根据线性组合形成控制量，然后对被控对象进行控制，其控制规律如下：

在上述公式中，KP、KI、Kd-比例、积分、微分增益。

PID控制方式可充分发挥KP、KI、Kd作用，由于其取值有所不同，比例、积分、微分的作用强弱也有区别。其中，KP能够决定水轮机系统控制作用强弱，如果KP较小，则系统所需时间也较长，如果KP较大，系统相应所需时间较短，这样很难保证系统运行稳定。有些被控对象具有自平衡特性和静差，通过增加KP，可减少静差，但是若KP较大，则动态性也会降低，进而影响闭环系统稳定性。另外，若KI过小，则会造成系统相应变慢，KI增大，则系统相应效率比较高，同时还可以对记忆误差积分，进而消除静差。如果Kd比较小，则微分效果比较差，随着Kd增加，在受到非最小相位环节的影响下，反调节也会随之增加。水轮机微分控制的优势在于可对误差进行微分处理，同时，对误差变化的敏感度较强。

4 PID参数整定方法

4.1 基于对象参数辨识的整定方法

在被控过程对象参数的辨识和整定过程中，需采用辨识方法对数学模型进行计算，再应用整定算法确定控制器参数。如果辨识方法、整定算法不同，整定方案也会有所不同。参数模型辨识法、非参数模型辨识法是两种常用的辨识办法，其中，在对象参数模型辨识方法的应用中，首先需假定一种模型结构，然后根据极小化模型，确定函数模型参数。若事先无法确定模型结构，则首先需要采用结构辨识的办法确定模型结构参数，然后再应用参数整定办法实现参数优化。

4.2 基于抽取过程对象输出响应特征值的控制器参数整定方法

基于对象模型辨识的参数整定操作便捷，由于对象模型中冗余信息量较大，因此，可能会对控制器参数整定造成不良影响，同时控制器参数并不是确定的，对此，首先需要对控制器进行整定处理，这样才能够包容对象模型，保障系统稳定性。根据对象输出相应特征值来实现PID参数整定的办法众多，比如闭环Z-N方法、继电整定法等等。

4 .3参数优化方法

从运筹学角度而言，控制器参数整定指的是在一定的条件约束下，对控制器参数进行调整，从而使得某个目标函数能够达最优值。在实际应用中，首先需提出合适的目标函数，采用寻优策略，对控制器参数进行整定，这样才能够反映出系统的调节情况：，式中，ts-指定过渡过程时间，ts0-参数x下系统过渡过程时间。，式中，Mp-指定超调量，M0p-参数X下系统超调量。

另外，还有一种目标函数是误差目标函数：

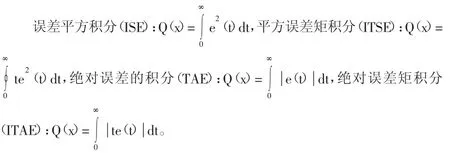
在参数优化方面，主要有两种方法，间接与直接优化。间接优化指的是首先写出目标函数，然后根据函数取值的充分条件和必要条件，计算最优参数；直接优化指的是首先对参数空间进行分析，根据一定的规律寻找最优参数，据此所获得的目标函数即为最小参数点。在参数优化时，无需被控对象的数学模型，只需采用试验办法，结合目标函数，即可获得相关系统动态特征量。

但是，参数优化也有局限性，具体体现在寻优目标函数的提取和确定方面。在选择目标函数过程中，无论是应用直接指定调节品质指标的方式，还是误差积分型指标，都有一定的局限性。除此以外，由于控制系统具有多值性特征，因此，在参数优化方面也有不足。对此，还应该积极研究相关优化方式，妥善解决参数整定问题。