西藏冷杉立木生物量和材积模型研建

陈振雄，贺东北，肖前辉，周湘江

（1.国家林业局 中南林业调查规划设计院，湖南 长沙 410014；2.西藏自治区林业厅 造林绿化处，西藏 拉萨 850000）

生物量和材积是我国乃至世界各国森林资源监测的重要内容，越来越受到重视。准确开展森林生物量和蓄积的监测和评估，建立合适的生物量和材积方程是一项十分重要的基础工作。由于生物量与材积紧密相关，近年来国内外学者在建立生物量模型的同时，更加注重兼顾与立木材积的协调性和相容性[1-3]。曾伟生等[4]在建立南方马尾松、东北落叶松和陈振雄等[5]在建立云南省云杉生物量时，均采用了非线性度量误差联立方程模型方法，建立了立木材积和生物量方程相容性模型。随着对生物量研究的深入，Bond-Lamberty等[6]在研究生物量时发现，如果林木胸径跨度较大时，采用单一整体模型拟合生物量方程，则会导致生物量估计值对胸径较小的林木产生系统性偏差；张连金等[7]在研究建立生物量模型时，将胸径在6 cm径阶以下的林木作为建模样本全部参与建模，发现林木胸径在2 cm径阶的估计偏差达到了20%以上，并采用带截距的非线性方程与分段建模方法消除了这种偏差。

西藏全区乔木林以冷杉面积、蓄积最大，分别占乔木林总面积、蓄积的30.53%、49.40%[8]，建立准确可靠的冷杉立木材积和生物量模型具有十分重要的意义。本研究基于冷杉立木材积和生物量实测数据，采用非线性度量误差联立方程组方法，在常规（整体）建模方法的基础上，进一步尝试分段建模方法，研究建立与材积相容性的立木生物量方程，并对2种方法进行对比分析，提出最为合适的方程，以期为科学评价西藏冷杉立木材积、生物生产力，制定生物量计量标准以及监测森林蓄积、固碳释氧能力、估算冷杉林分碳汇能力等提供理论依据。

1 数据采集

数据来源于2011年西藏冷杉生物量调查建模项目，共实地采集冷杉样木150株，采集地点主要集中在西藏林芝地区，全部为天然起源。按2、4 cm径阶距设定约10个径阶组选取样木，每个径阶组选取的样木数量基本一致（约 15 株），并充分考虑林分密度（高径比）、龄组结构、立地条件、地域地貌分布和林木冠幅、冠长等因子要求，确保样木在西藏全区范围具有充分的代表性。

样木采伐前先测量地径、离地10 cm高度处直径、胸径和冠幅，采伐后再测量第一活枝高度、总树高（H），以及相对树干高0.05H、0.1H、0.2H、0.3H、0.4H、0.5H、0.6H、0.7H、0.8H、0.9H处带皮直径。每株样木分干、皮、枝、叶称总鲜质量和采样，测定样品含水率，再推算、汇总得到地上总生物量。对其中约1/3（49株）样木的所有根系全部挖出，分根系类别（主根、粗根、细根、须根）称总鲜质量和采样，同样测定样品含水率，并推算、汇总得到地下总生物量。西藏冷杉立木生物量和材积数据基本情况详见表1。

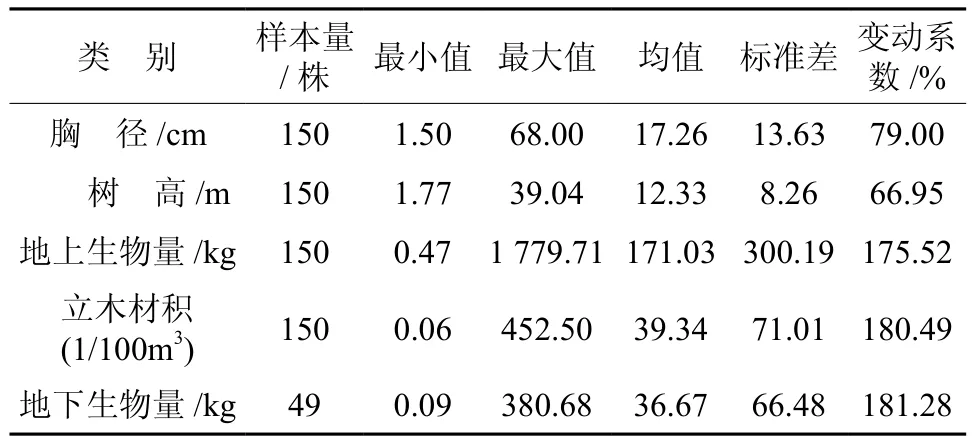
表1 冷杉生物量和立木材积数据基本情况Table 1 General situations of tree volumes and biomass sample of Abies

2 研究方法

2.1 地上生物量与材积相容性方程建模方法

通常对所有样本进行单一整体建模，设计的生物量与材积相容的非线性度量误差联立方程组方法[9]如下：

式（1）、（2）中：M、V、D、H分别代表地上生物量（kg）、立木带皮材积（1/100 m3）、胸径（cm）和树高（m）；ai、bi、ci（i=0，1，2）为方程参数。将式（1）、（2）作为联立方程组，采用非线性度量误差模型方法，一并求解各个参数，将D、H两个因子作为无误差变量，V、M两个因子作为误差变量[10]。式（2）中，方程c0Dc1Hc2即是立木材积与地上生物量两者之间的二元转换模型。如果只考虑胸径（D）的一元模型，则去掉式（1）、（2）中的树高（H）项即可。

由于冷杉样本胸径跨度较大（1.5～68 cm），进一步分析发现，采用上述方法对所有样本进行整体建模，得到的冷杉立木材积和地上生物量方程均导致16 cm径阶以下样木的估计结果产生明显偏差。因此，再采用分段建模方法进行建模。为便于模型的实用性，本文分两段进行建模，假设以胸径大小为D0作为分段模型的结点，则建立分段相容性二元立木材积和生物量模型结构[7,11]如下：

式（3）～（6）中：V1、V2代表立木材积；M1、M2代表地上生物量。为确保分段模型在分节点D0处平滑无缝衔接，则分段模型参数aij、bij、cij（i=1，2；j=1，2，3）之间相关关系要满足如下等式条件：

先利用胸径D0以上样木数据，采用非线性度量误差联立方程组联合估计式（3）、（4）的参数；再根据式（7）、（8）的限制条件，利用胸径D0以下样木数据估计联合方程组式（5）、（6）的参数。对于一元模型，只需相应去掉H项的参数即可。

2.2 地下生物量方程建模方法

地下生物量模型通常也以胸径（D）或树高（H）作为自变量进行建模。根据相关研究[4-5,12]，相比较以胸径为自变量的一元地下生物量模型，以树高、胸径为自变量的二元地下生物量模型改进效果不大。因此，只研究建立以胸径为自变量的一元地下生物量模型。由于地下生物量与地上生物量存在较高的相关性，参照上面地上生物量与立木材积相容性方程建模方法，建立相容性地下生物量模型：

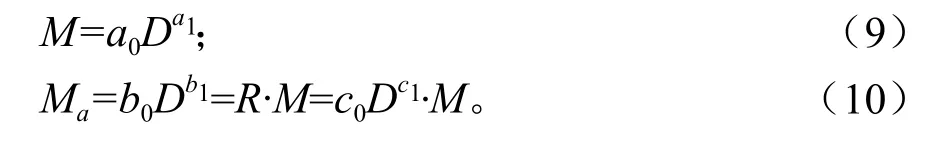
式中：M、Ma、D分别代表地上总生物量（kg）、地下总生物量（kg）、胸径（cm）；ai、bi、ci（i=0,1）为方程参数。方程R=c0Dc1即为地下和地上生物量换算方程（根茎比方程）。将式（9）、（10）作为联立方程组，将D作为无误差变量，Ma、M作为误差变量，采用非线性度量误差联立方程组方法联合估计求解参数值。

2.3 异方差性消除

基于立木材积、生物量数据普遍存在异方差性这一特点[13]，必须采用有效方法消除其影响。根据每个独立拟合方程的方差，建立以胸径为一元的权函数，采用加权回归方法进行消除。

2.4 模型评价方法

为了对建立的西藏冷杉整体模型与分段模型的拟合效果进行科学检验与评价，采用如下评价指标：确定系数（R2）、标准误差（SEE）、预估精度（P）、相对偏差（TRB）、系统偏差（MSB）和百分标准误差（MPSE）。各指标计算公式[14]如下：

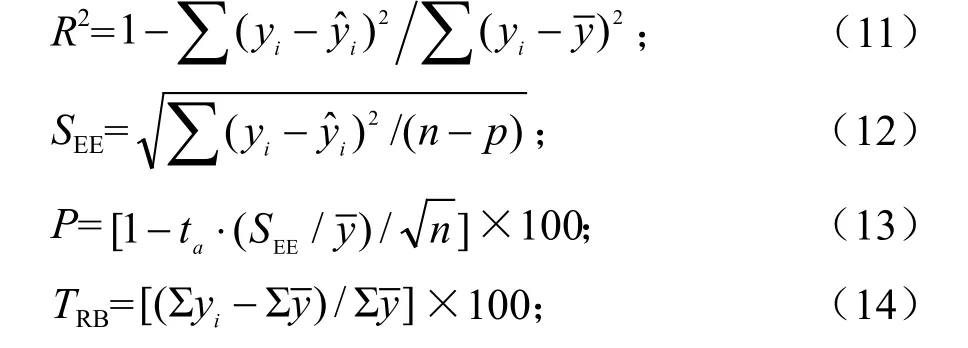
3 结果与分析

3.1 材积与地上生物量方程拟合结果

利用西藏冷杉150株样木的地上生物量和材积实测数据，按一元（D）和二元（D、H）模型结构，先将全部样木作为建模样本，采用单一方程进行整体建模；然后再将样本分为两部分，进行分段建模。为找到分段建模的合适节点，选取不同胸径大小分别进行建模对比分析，发现分段节点设定在材积（生物量）随胸径变化趋势曲线中急剧增加的位置附近时，模型改进效果明显，最终将胸径D0设定为15 cm作为分段建模的节点。计算得到整体模型和分段模型的参数估计值详见表2，方程检验统计指标结果详见表3。

表2 冷杉分段建模和整体建模拟合方程参数估计值Table 2 Parameter estimation of fitting equations for the segmented model and whole model of Abies

从表3可以看出，不管是整体模型还是分段模型，从总体水平上来看，一元、二元整体模型与分段模型的各项统计指标相差不大。相比较一元模型，二元整体模型和分段模型拟合效果均有明显改进效果，其中立木材积预估精度均提高约4%，地上生物量预估精度均提高约1.5%。研究建立的二元整体模型和分段模型，两者立木材积方程的确定系数R2都在0.981 0以上，预估精度（P）都在96.1%以上；两者二元地上生物量方程的确定系数R2都在0.956 0以上，预估精度（P）在94.7%以上；一元整体模型和分段模型的地上生物量与立木材积方程确定系数R2均在0.941 0以上，预估精度（P）均在93.3%以上。

表3 冷杉分段建模和整体建模拟合方程统计指标Table 3 Statistical indicators of the fitting equations for the segmented model and whole model of Abies

再进一步分径阶进行检验分析，得到二元、一元整体建模和分段建模分径阶比较结果（见表4、表5）。由表4和表5可以看出，不论是一元模型还是二元模型，采用整体建模得到的径阶16 cm以下的林木立木材积和生物量估计值均小于实际值，径阶越小，偏差越大。在4 cm径阶处，一元、二元整体模型立木材积的TRB分别达到了32.60%、19.32%，地上生物量的TRB分别达到了35.41%、23.25%。而采用分段建模方法建立的模型，得到各径阶立木材积和生物量估计值均不存明显的偏差。一元分段模型立木材积和地上生物量方程各个径阶的TRB基本控制在±12%以内，二元分段模型立木材积和地上生物量方程各个径阶的TRB都能控制在±7%以内。绘制二元整体模型和二元分段模型立木材积、地上生物量相对残差散点分布，结果见图1、图2，一元模型残差图与二元模型基本类似，限于篇幅而未一一列出。图1充分反映出二元整体模型在2～16 cm径阶明显存在估计值偏小的问题，而图2则充分反映出二元分段模型各个径阶的残差以0为基线呈随机对称分布，无明显的系统偏差。

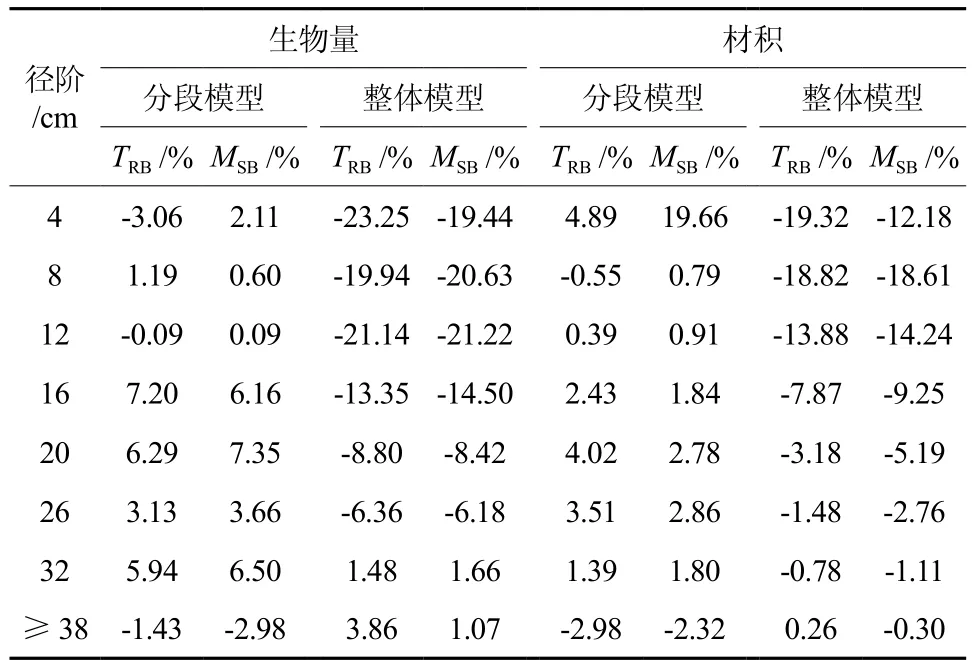
表4 二元整体建模和分段建模分径阶比较结果Table 4 The comparison results between two variablebased segmented model and whole model by diameter classes

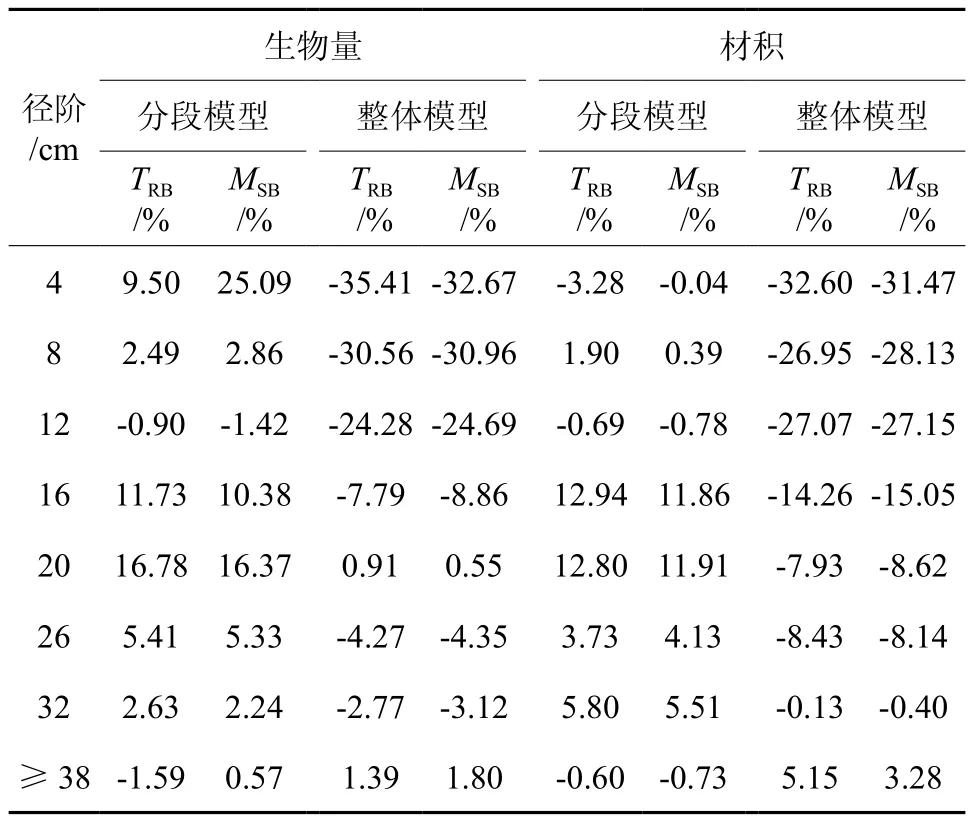
表5 一元整体建模和分段建模分径阶比较结果Table 5 The comparison results between one variablebased segmented model and whole model by diameter classes

3.2 地下生物量方程拟合结果

利用式（9）、（10）联立，求解得到西藏冷杉一元地下生物量和地上生物量相容性模型参数与检验统计指标，结果见表6、表7。从表7可以看出，一元地下生物量模型拟合效果良好，确定系数R2为0.961 9，预估精度为90.12%。由于采集地下生物量难度大，挖根实测地下生物量样本仅占总数的1/3。根据《立木生物量建模方法技术规程》[15]的要求，当地下生物量样本是地上生物量的子样本时，则用所有样本建立的地上生物量模型与根茎比模型换算得到地下生物量模型，即用表6的根茎比模型与表2中的一元地上生物量分段模型相乘，从而得到地下生物量分段模型（见表8）。根据误差传播相关规律[16]，计算根茎比模型和一元分段模型总预估误差的平方平均数，即是最终地下生物量模型的平均预估误差，得到一元分段地下生物量模型总预估精度为91.67%，高于表7的90.12%。

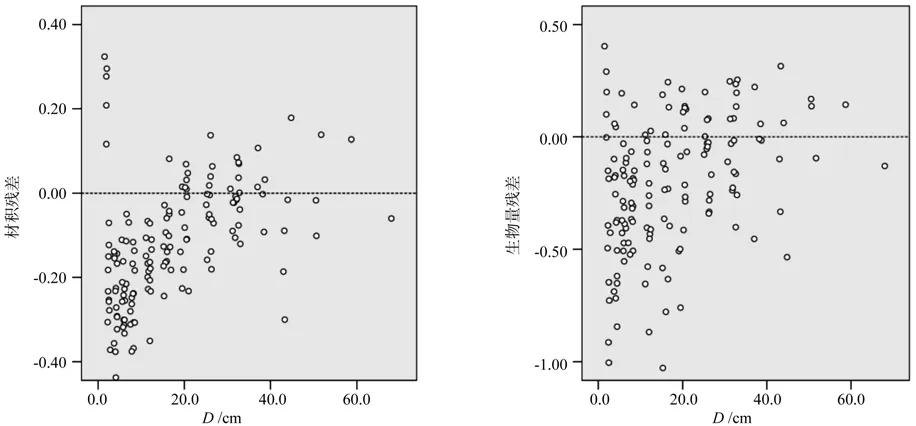
图1 二元整体模型得到的立木材积和生物量相对残差分布Fig.1 The relative residuals errors of tree volume and biomass with DBH (D) distribution in two variable-based whole model

图2 二元分段模型得到的立木材积和生物量相对残差分布Fig.2 The relative residuals errors of tree volume and biomass with DBH (D) distribution in two variable-based segmented model

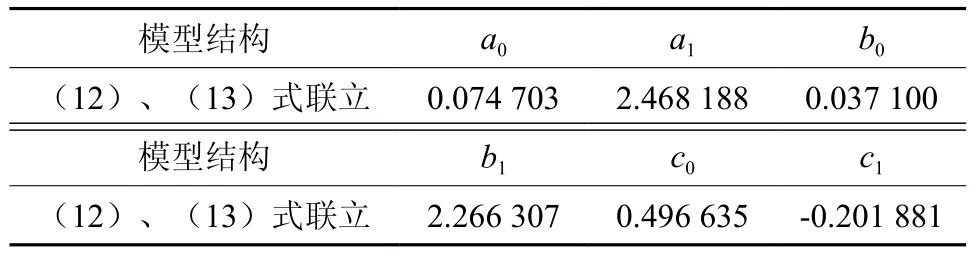
表6 冷杉相容性地下生物量拟合方程参数估计值Table 6 Parameter estimation of fitting equations for the below-ground biomass model of Abies

表7 冷杉相容性地下生物量拟合方程统计指标Table 7 Statistical indicators of fitting equations for the below-ground biomass model of Abies

表8 由表6的根茎比模型和表2一元分段地上生物量模型得到的地下生物量分段模型Table 8 Parameter estimates and P values of belowground biomass equations obtained from rootshoot ratio equations in table 6 and aboveground biomass equations in table 2

4 结 论

本研究以西藏冷杉作为研究对象，利用非线性度量误差联立方程组方法进行整体建模和分段建模，分别研究建立了与材积相容的冷杉生物量方程，并对两者拟合效果进行了对比分析，可以得到如下主要结论：

（1）利用非线性度量误差联立方程组方法，可以较好地解决立木材积与生物量、地下生物量与地上生物量方程之间参数衔接一致性与相容问题；而采用分段建模方法可以较好地改进建模效果，并实现分段节点处两段方程估计值的平滑无缝对接，保证两段方程在结点处的估计结果一致。

（2）采用单一整体模型，难以准确描述西藏冷杉生物量、材积随胸径变化情况, 且难以保证模型各个径阶（尤其是小径阶）的立木生物量估计精度。不论是一元模型还是二元模型，采用整体建模得到冷杉径阶16 cm以下的林木立木材积和生物量估计值均小于实际值，径阶越小，偏差越大，其中4 cm径阶的预估偏差甚至可以达到20%～30%。

（3）采用分段建模方法能有效解决冷杉立木材积和生物量在小径阶林木有偏估计的问题，本研究将分段节点设定在材积（生物量）随胸径变化趋势曲线中急剧增加的位置附近（15 cm），分段模型改进效果良好，各径阶均无系统偏差。分段建立的地上生物量和立木材积方程，不论一元或二元模型，其预估精度分别达到了93.5%、92.8%以上；一元分段地下生物量方程预估精度也在91.5%以上。在生产应用中，推荐使用研究建立的分段模型。

采用分段建模时，找到一个合适的分段节点，是改进分段建模效果的一个核心问题，通常做法是选取不同节点位置预先建模对比分析来解决，此方法较为繁琐，且较难找到其最佳分节点。如何就不同建模样本，快速确定分段建模的最佳分节点，找出具有普遍意义的分段规律，有待于下一步深入研究。

[1]骆期邦,曾伟生,贺东北,等.立木地上部分生物量模型的建立及其应用研究[J].自然资源学报,1999,14(3):271-277.

[2]曾伟生,骆期邦,贺东北.兼容性立木生物量非线性模型研究[J].生态学杂志,1999,18(4):19-24.

[3]唐守正,张会儒,胥 辉.相容性生物量模型的建立及其估计方法研究[J].林业科学, 2000,36(专刊1): 19-27.

[4]曾伟生,张会儒,唐守正.立木生物量建模方法[M].北京:中国林业出版社,2011.

[5]陈振雄,贺东北,甘世书.云南省云杉立木生物量模型研建[J].中南林业调查规划,2011, 30(4):56-61.

[6]Bond-Lamberty B, Wang B C, Gower S T. Aboveground and below-ground biomass and sapwood area allometric equations for six borealtree species of northern Manitoba[J].Can. J. For.Res., 2002, 32(8):1441-1450.

[7]张连金,曾伟生,唐守正.用带截距的非线性方程和分段建模方法对立木生物量估计的比较[J].林业科学研究,2011, 24(4):453-457.

[8]贺东北,陈振雄,柯善新,等.西藏自治区第二次森林资源规划设计调查报告[R].长沙:国家林业局中南林业调查规划设计院,2014.

[9]唐守正,郎奎建,李海奎. 统计和生物数学模型计算（ForStat教程）[M].北京:科学出版社,2009.

[10]曾伟生,唐守正.利用度量误差模型方法建立相容性立木生物量方程系统[J].林业科学研究,2010,23(6):797-802.

[11]党永峰,王雪军,曾伟生.用分段建模方法建立东北落叶松立木材积和生物量方程[J].林业科学研究, 2012,25(5):558-563.

[12]曾伟生,肖前辉,胡 觉,等. 中国南方马尾松立木生物量模型研建[J].中南林业科技大学学报,2010,30(5):50-56.

[13]骆期邦,曾伟生,贺东北.林业数表模型理论、方法与实践[M].长沙:湖南科学技术出版社, 2001.

[14]陈振雄,贺东北,贺 鹏.利用混合模型方法建立海南省橡胶树立木材积方程[J].中南林业科技大学学报,2016,36(12):31-36.

[15]国家林业局.LY/T 2258-2014立木生物量建模方法技术规程[S].北京:中国标准出版社,2014.

[16]曾伟生,唐守正.东北落叶松和南方马尾松地下生物量模型研建[J].北京林业大学学报,2011,33(2):1-6.