移树机大臂机构多目标参数优化及试验

，，，，，

(1.浙江理工大学，a.机械与自动控制学院；b.浙江省种植装备技术重点实验室，杭州 310018；2.浙江三锋实业股份有限公司，浙江 金华 321300)

0 引 言

随着我国经济的不断发展和生活水平的不断提高，人们对生活环境的要求也越来越高，尤其注重城市生态环境的建设，而城市生态环境建设又以城市绿化为重点[1-2]，由于城市环境的局限性，树木移栽成为短时间迅速提高城市绿化水平的有效途径[3-4]。以往树木移栽大多都是以人工移栽为主，但人工移栽存在劳动强度大、人工成本高、移栽规模小、移栽效率低等缺陷[5-6]，而机械化移栽可提高几十倍甚至上百倍效率，因此，机械化移栽技术就成为当今亟需普及并进一步提高的树木移栽技术[7-8]。

树木机械化移栽技术的实现主要依托移树机来完成。目前市面上已经有多种树木移植机，它们的工作原理和适用范围不尽相同，但大多数移树机都是靠大臂机构来完成树木移植工作的[9-13]。移树机的大臂机构由液压缸驱动，大臂末端带动铲片运动完成树木移植，大臂机构参数决定机构的运动性能和功耗。

目前的移树机大臂机构虽然能带动铲片完成树木移植，但是移植过程大臂末端的轨迹不是直上直下，而是沿着移树机前进方向有较大的摆动，这样就增加了功耗和操作难度。目前尚未发现对移树过程中大臂的做功进行研究和优化的报道。本文在大臂机构运动学分析和动力学分析的基础上，以移树过程中液压缸的做功最小和大臂末端轨迹前摆动量最小为优化目标，以大臂的结构空间和工作空间运动时不发生干涉以及满足构件间传动角要求为约束条件，建立了移树机大臂机构参数优化模型，并进行参数优化、分析和试验。

1 移树机大臂机构运动学分析模型的建立

1.1 移树机大臂机构

移树机大臂机构简图如图1所示，该机构为一单自由度六杆机构，包括原动件(液压缸)BE、连杆DEF、连架杆AD和CF，点A、B、C、D、E、F为铰链点，杆EMP和连杆DEF固连，末端P将与植树机的铲片组相连。当液压缸行程增加并绕B点转动时，连杆DEF将绕E点转动，连架杆AD绕A点转动，连架杆CF绕C点转动，末端P将实现预定轨迹的上升运动。

1.2 大臂机构运动学分析模型的建立

为了对机构进行运动学分析，建立以铰链点A为坐标原点(0,0)的直角坐标系(如图1所示)，将各构件表示为杆矢，并将各杆矢用指数形式的复数表示[14-16]。为分析方便，本文中所涉及的参数及说明列于表1。

图1 大臂机构简图

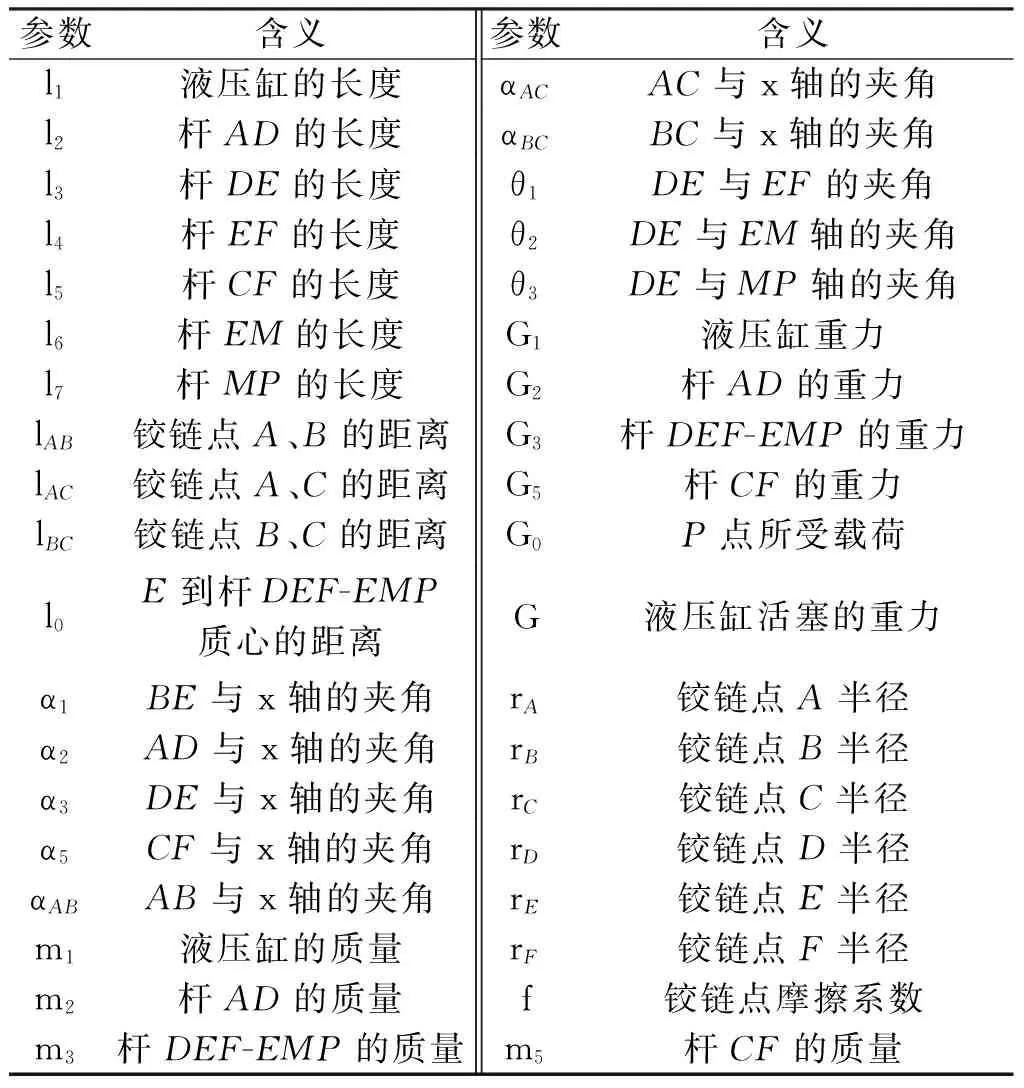
参数含义参数含义l1液压缸的长度αACAC与x轴的夹角l2杆AD的长度αBCBC与x轴的夹角l3杆DE的长度θ1DE与EF的夹角l4杆EF的长度θ2DE与EM轴的夹角l5杆CF的长度θ3DE与MP轴的夹角l6杆EM的长度G1液压缸重力l7杆MP的长度G2杆AD的重力lAB铰链点A、B的距离G3杆DEF-EMP的重力lAC铰链点A、C的距离G5杆CF的重力lBC铰链点B、C的距离G0P点所受载荷l0E到杆DEF-EMP质心的距离G液压缸活塞的重力α1BE与x轴的夹角rA铰链点A半径α2AD与x轴的夹角rB铰链点B半径α3DE与x轴的夹角rC铰链点C半径α5CF与x轴的夹角rD铰链点D半径αABAB与x轴的夹角rE铰链点E半径m1液压缸的质量rF铰链点F半径m2杆AD的质量f铰链点摩擦系数m3杆DEF-EMP的质量m5杆CF的质量

a) 位移分析

由封闭图形ADEFCA可得到机构第一个封闭矢量方程：

(1)

由封闭图形ADEBA可得到机构第二个封闭矢量方程：

(2)

由封闭图形BEFCA可得到机构第三个封闭矢量方程：

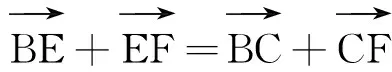
(3)

将矢量方程(1)—(3)联立得到其复数形式为：

(4)

将方程组(4)的实部和虚部分离，得：

(5)

通过对方程组(5)进行非线性方程组求解，可求得α1、α2、α3、α5的值。

AD杆质心坐标为：

(6)

BE质心坐标为：

(7)

CF杆质心坐标为：

(8)

DEF-EMP杆质心坐标为：

(9)

b) 速度分析

求方程组(6)一阶导数，得AD杆质心速度为：

(10)

求方程组(7)一阶导数，得BE质心速度为：

(11)

求方程组(8)一阶导数，得CF杆质心速度为：

(12)

求方程组(9)一阶导数，得DEF-EMP杆质心速度为：

(13)

c) 加速度分析

求方程组(6)二阶导数，得AD质心加速度为：

(14)

求方程组(7)二阶导数，得BE质心加速度为：

(15)

求方程组(8)二阶导数，得CF质心加速度为：

(16)

求方程组(9)二阶导数，得DEF-EMP质心加速度为：

(17)

2 大臂机构动力学分析模型的建立

为求解大臂机构各铰链点处的受力情况，首先对机构中各构件进行受力分析，如图2、图3所示。

图2 构件受力分析

图3 机构受力分析

分析构件AD受力情况，动力学平衡方程为：

(18)

(19)

∑MA=FDyl2cosα2-FDxl2sinα2-

(20)

分析构件BE受力情况，动力学平衡方程为：

(21)

(22)

∑MB=FEyl1cosα1-FExl1sinα1-

(23)

分析构件CF受力情况，动力学平衡方程为：

(24)

(25)

∑MC=FEyl5cosα5-FFxl5sinα5-

(26)

分析构件DEF-EMP受力情况，动力学平衡方程为：

(27)

(28)

∑ME=-FDxl3sinα3+FDyl3cosα3+

FFxl4sin(α3+θ1)-FFyl4cos(α3+θ1)-

G0[l6cos(α3+θ2)+l7cos(α3+θ3)]-

(29)

联立方程(18)—(29)可求得大臂机构各铰链点处的受力情况，若要求解液压缸活塞受力情况，则需要对液压缸活塞进行受力分析，如图4所示，FN表示液压缸活塞受到的内部压力，Ft表示液压缸壁对活塞的压力，G表示液压缸活塞的重力。

图4 液压缸活塞受力分析

分析液压缸活塞受力情况，动力学平衡方程为：

∑Fx=FEx-Ft·sinα1+FN·cosα1=0

(30)

∑Fy=FEy+Ft·cosα1+FN·sinα1-G=0

(31)

联立方程(30)(31)可求得活塞所受内部压力FN。

3 大臂机构多目标参数优化数学模型的建立

3.1 设计变量的确定

大臂机构的运动性能、传动性能、末端的运动轨迹以及工作过程中的能耗取决于各杆件的长度和固定铰链点的位置，而与铰链点的半径(rA、rB、rC、rD、rE、rF)并没有直接的联系，另外，杆EM和杆MP是与杆DEF固连的外伸端，其长度(l6、l7)并不影响大臂机构的运动性能，故在文中将这些参数设成定值。表1中的θ1、θ2、θ3分别为杆DE与杆EF、杆EM和杆MP的夹角，在计算过程中是保持不变的，也为定值。故本文选取连架杆AD长度l2，杆件DE长度l3，杆件EF长度l4，连架杆CF长度l5，铰链点A、B之间的距离lAB以及铰链点B、C之间的距离lBC作为设计变量，即：X=[l2,l3,l4,l5,lAB,lBC]。而表一中提到的各杆质量mi，各杆重力Gi，各杆与x轴夹角αi都是杆长的函数，可以根据杆长求得，故不设为变量。

3.2 目标函数的建立

为了获得大臂机构的最佳传动性能，并减小工作过程中液压缸做功，本文采用多目标优化设计的方法[17-19]，其数学模型中各分目标函数考虑如下：

a)为了减小整台机器的功率，减小能耗，应使大臂机构中的液压缸在工作过程中做功达到最小，其目标函数用F1(x)表示，数学表达式为：

其中：FN为工作过程中任意时刻液压缸内部压力，s为液压缸行程。

设P点的实际运动轨迹为Pi(xPi,yPi)，目标运动轨迹为直线P0P，如图5所示。P0为最低点，其坐标为(x0,y0)(其中，x0为xPi的平均值)，P为最高点，其坐标为(x,y)，其中，x=x0，y=y0+h，h为树木被抬升的高度，则P0P的直线方程为x=x0。

图5 大臂机构末端运动轨迹摆动量的评价

实际轨迹点Pi(xpi,ypi)到直线P0P的垂直距离di=|xpi-x0|。为了使Pi的点实际运动轨迹以最高的精度接近期望的直线，要求Pi点在yi到y这一段高度范围内误差的均方差最小，即F2(x)的值最小。

综合考虑上述两个子目标函数，建立本文目标函数：

minF(x)=λ1F1(x)+λ2F2(x).

其中λ1、λ2为加权因子。而本文将减小整机工作能耗作为优化的主要目标，虽然改善大臂末端运动轨迹的目的也是为了减小工作能耗，但减小的幅度有限，并且在后续的程序运算中发现：在λ1=0.5，λ2=0.5；λ1=0.6，λ2=0.4；λ1=0.7，λ2=0.3；λ1=0.8，λ2=0.2；λ1=0.9，λ2=0.1五组取值中，采用第二组取值方法得到的目标函数值最为可观，故本文取λ1=0.6，λ2=0.4。

3.3 约束方程的建立

根据大臂的结构空间和工作空间、运动时不发生干涉以及传动性能良好的要求，对机架和其他各杆件的长度、机构的传动角大小有一定的限制，都可统一表达为以下形式：

X(i)min≤X(i)≤X(i)max，i=1,2,3,4,5,6.

其中：X(i)max为第i个变量的上限，X(i)min为第i个变量的下限。本文设计变量的上下限分别为：400≤X(1)≤500，530≤X(2)≤630，420≤X(3)≤520，1200≤X(4)≤1350，1030≤X(5)≤1200，1670≤X(6)≤1800,机构传动角γ≥40°。

至此，植树机大臂机构的设计已被转化为6个优化参数、7个不等式约束的优化问题。

4 大臂机构优化模型求解

大臂机构优化计算中需要求出全局最优解，则应选择能够解决高度非线性优化问题的全局优化算法，本文选择遗传算法作为最优化搜索方法[20-23]。

4.1 辅助优化软件的编写及应用

基于MATLAB软件编写了优化程序，如图6所示。区域1为参数输入区，用来输入初始值；区域2和区域4为结果显示区，区域2用来显示优化结果，区域4用来显示初始目标函数和优化目标函数值；区域3为控制键区，有优化计算、目标函数计算、初始轨迹、优化轨迹共四个按钮键，根据需要按不同的键可以实现各个功能；区域5为仿真输出区，分别显示大臂机构的初始运动仿真和优化后的运动仿真。

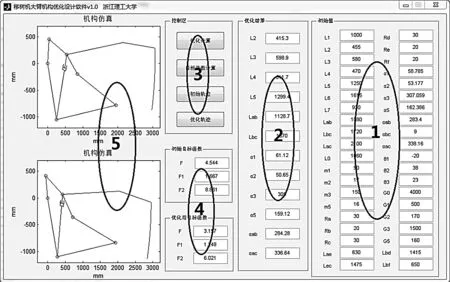
图6 移树机大臂机构优化设计软件界面

取现有某型号移树机大臂机构的参数为初始解，如表2所示，将此初始解输入图6软件中的区域1，经过优化计算，可得到区域2中的优化结果，同时可得到区域4中初始目标函数值和优化后的目标函数值，以及区域5中初始机构运动仿真和优化机构运动仿真图。

表2 某型号移树机大臂机构参数

4.2 参数优化结果及分析

遗传算法存在一定的随机性，通过多次计算发现：当遗传算法迭代141次，目标函数值趋于稳定，141次以后，目标函数值不再变化或存在极微小的变化，说明优化终止，故本文取遗传算法迭代141次所得设计变量的值为最终的优化结果，目标函数的具体变化过程如图7所示。优化计算结果为：X=[415.3,598.9,511.7,1299.4,1128.7,1670]，目标函数值F=3.157，其中：液压缸做功F1=1.248，机构末端P的实际运动轨迹与期望运动轨迹误差F2=6.021；初始条件的目标函数值F=4.5443，其中：液压缸做功F1=1.6668，机构末端P的实际运动轨迹与期望轨迹误差F2=8.8607。

图7 遗传算法结果

与初始条件对应的目标函数相比，优化计算结果中的两个子目标函数的值都有明显的减小，其中，液压缸做功为原来的74.87%，同时，当两机构末端上升相同高度时，优化后的机构液压缸行程为183 mm，而优化前的机构液压缸的行程为250 mm，这都说明通过本文方法优化后的大臂机构起到了明显的减小整机能耗的作用；优化后大臂末端轨迹前后摆动量为原来的67.95%，说明优化后的大臂机构末端直线上升的效果要比优化前的机构好，这一点通过图8中两机构末端的运动轨迹对比得到了很好的证明。

图8 优化前后大臂机构末端运动轨迹

5 试 验

依据优化结果加工出相应尺寸的大臂机构，将大臂机构安装在装载机上并进行试验，大臂机构末端轨迹的高速摄像分析结果界面如图9所示。用高速摄影拍摄到大臂末端的运动轨迹如图9中运动轨迹线所示，从图中可以看出，大臂末端实际运动轨迹与优化所得的理论运动轨迹相吻合，进一步证实了本文所建的优化模型是可靠的、有效的。

图9 大臂机构末端轨迹的高速摄像分析

6 结 论

本文建立了移树机大臂机构的运动学分析模型、动力学分析模型和机构参数优化模型。

通过MATLAB软件，编写移树机大臂机构优化设计软件，运用有约束优化算法求得本机构的最优解：l2=415.3 mm，l3=598.9 mm，l4=511.7 mm，l5=1299.4 mm，lAB=1128.7 mm，lBC=1670 mm，目标函数值从优化前的F=4.5443变为F=3.157，其中：液压缸做功从优化前的F1=1.6668变为F1=1.248，机构末端P的实际运动轨迹前后摆动量由优化前的F2=8.8607变为F2=6.021。通过对优化前后目标函数值的对比，发现优化后功耗为原来的74.87%，优化后大臂末端轨迹前后摆动量为原来的67.95%。

根据优化结果加工出大臂机构，并将大臂机构安装在装载机上进行试验，用高速摄影拍摄得到大臂机构末端的实际运动轨迹，比较实际运动轨迹和理论运动轨迹，发现两者是相吻合的，证明本文所建的优化模型是可靠的、有效的。

[1] 李春高．我国造林机械的现状及发展趋势[J]．林业机械与木工设备，2012，40(10)：4-10．

[2] 宋代平，王正祥，张云秀，等．生态植树机发展综述[J]．林业机械与木工设备，2004，32(4)：4-6．

[3] 武广涛，俞国胜，李美华．国内造林机械及发展前景[J]．林业机械与木工设备，2003，31(11)：4-5．

[4] 于晓旭，赵匀，陈宝成，等．移栽机械发展现状与展望[J]．农业机械学报，2014，45(8)：44-53．

[5] 赵德金，艳玲，文龙．国内外树木移植机械的研究现状与发展趋势[J]．安徽农业机械，2014，42(18)：6064-6067．

[6] 顾正平，沈瑞珍．树木栽植与养护机械发展概况[J]．世界林业研究，2005，18(4)：40-44．

[7] 于建国，屈锦卫．国内外挖坑机的研究现状及发展趋势[J]．农机化研究，2006(12)：38-41．

[8] Solazzi L. Design of aluminium boom and arm for an excavator[J]. Journal of Terramechanics,2010,47(4):201-207．

[9] 潘玉安，程洪涛，姜迪友，等．基于ADAMS的挖掘机工作装置的仿真与优化设计[J]．煤矿机械，2009，30(3)：15-17．

[10] 胡飞，尹文庆，陈彩蓉．基于MATLAB的移栽机械臂运动学分析与仿真[J]．江西农业学报，2012，24(12)：151-153．

[11] 李耀明，徐立章，陈航．4YS-600型树木移栽机铲刀臂的改进设计[J]．农业工程学报，2009，25(3)：60-63．

[12] 孟兆新，王亮亮，范恒博．基于有限元的树木移植机铲刀挖掘力分析[J]．森林工程，2014，30(2)，75-78．

[13] 张秀玲．WYL120轮胎式液压挖掘机动臂结构分析与优化研究[D]．福州：福建农林大学，2012．

[14] 代丽，孙良，赵雄，等．基于运动学目标函数的插秧机分插机构参数优化[J]．农业工程学报，2014，30(3)：36-42．

[15] 雷经发，扈静，魏涛．基于MATLAB的平面四杆机构运动学分析[J]．机械工程师，2009(9)：76-78．

[16] 李建霞，王良才．基于Matlab的四杆机构优化设计简介[J]．机电产品开发与创新，2010，23(1)：88-90．

[17] 卞学良，肖汾阳，马国清，等．装载机连杆式动臂工作装置多目标优化[J]．工程机械，2002(12)：13-15．

[18] 陈剑，葛文杰，王军强，等．平面四杆机构参数化设计及运动仿真研究与实现[J]．中国制造业信息化，2010，39(9)：24-30．

[19] Sui T Z, Wang L, Tan Z, et al. Structural parameters optimization of excavator working device based on mining process[J]. Advanced Materials Research,2011,421:759-763.

[20] 张国平．食品机械平面四杆机构的遗传算法优化设计[J]．食品与机械，2010，26(3)：117-120．

[21] 翟力欣，姬长英，丁启朔，等．犁体结构参数与工作参数优化设计[J]．农业机械学报，2013，44(8)：57-62．

[22] 王春水，肖学柱，陈汉明．遗传算法的应用举例[J]．计算机仿真，2006，22(6)：155-157．

[23] 周明刚，张露，陈源，等．基于灵敏度分析的船式拖拉机机架结构优化设计[J]．农业工程学报，2016，32(12)：54-60．

[24] 王金武，张春凤，周文琪，等．基于MATLAB仿真的非规则齿轮行星系扎穴机构的优化设计[J]．农业工程学报，2016，32(3)：22-28．

[25] 郑惠强，王业文．液压挖掘机动臂优化设计数学建模的建立[J].中国工程机械学报，2006，2(4)：142-144．