摆动导杆驱动的小型旋转折叠翼动力学仿真

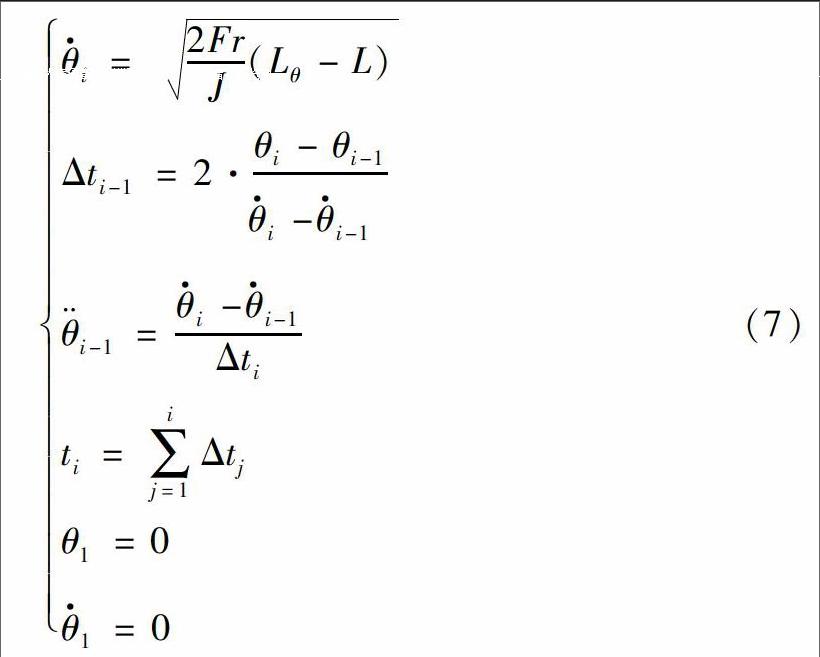
摘 要： 通过配置旋转折叠翼可显著增加小型制导炸弹的飞行距离。为了验证旋转折叠翼的展开性能， 对一种摆动导杆驱动的小型旋转折叠翼方案进行研究。 应用理论力学的动能定理， 得出了理想化模型的展开运动方程， 并通过MATLAB进行数值求解； 应用多体系统动力学理论， 在ADAMS中建立了该方案的虚拟样机， 通过PECE预估校正算法， 仿真分析了动力学运动规律。仿真结果表明两种分析方法得出的小型旋转折叠翼展开运动规律相同； 满载情况下， 该方案的展开时间满足设计要求。

关键词： 小型旋转折叠翼； 动力学仿真； MATLAB； ADAMS

中图分类号： TJ760.3+4； V421文献标识码： A文章编号： 1673-5048（2017）06-0054-05[SQ0]

0 引 言

小型旋转折叠翼具有轻巧灵活， 便于机载发射的优点， 可在展开后为小型制导炸弹提供升力， 显著增加了小型制导炸弹的飞行距离， 是一种低成本、 高性能的增程组件。随着小型精确制导武器的发展， 对小型旋转折叠翼技术的研究备受武器工业界的关注。

2010年， 美国洛克希德·马丁公司完成了“蝎子”小型滑翔制导炸弹的飞行试验。该款制导炸弹采用了旋转式折叠翼， 在1 524 m的高度从通用发射管发射后， 展开折叠翼， 滑翔3 km后精确飞抵目标。

2016年， 美国动力公司推出的新型管发小型滑翔弹药“GBU-69B”获得了美国特种作战司令部的订单。该款小型滑翔弹药同样配置了小型旋转式折叠翼。

小型旋转折叠翼展开动力学的性能评价参数主要包括： 展开时间、 展开角度、 展开过程角速度和展开过程角加速度等。上述参数直接影响到小型制导炸弹投放后能否正常飞行和成功完成预定任务。为获得小型旋转折叠翼展开动力学的各项性能指标， 需对其展开机构进行动力学仿真研究。

1 小型旋转折叠翼组成及工作原理

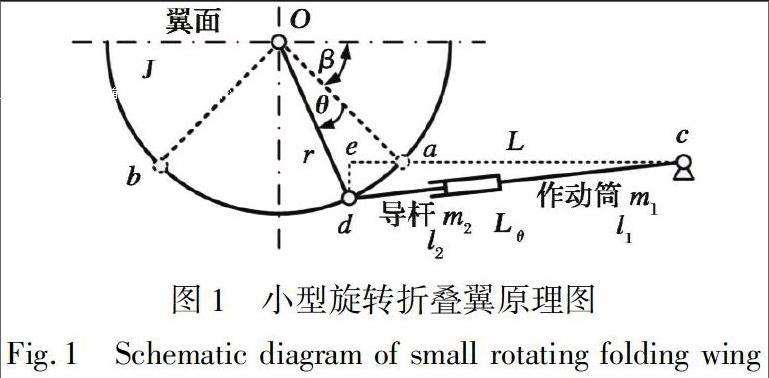
摆动导杆驱动的小型旋转折叠翼主要由翼面、 导杆和作动筒组成， 翼面应在承受最大升力2 000 N和阻力666.7 N的情况下， 在0.5 s的时间内旋转90°后展开到位。具体工作原理如图1所示。

翼面可绕点O旋转， 初始点a处与导杆铰链连接； 作动筒一端用铰链固定于c点， 一端与导杆以活塞形式配合连接， 作动筒内部放置可产生高压气体的火药； 当旋转折叠翼需展开时， 通过电路触发点燃火药， 产生的高压气体推动导杆前移， 推动翼面旋转； 翼面旋转90°后， a点移动至b点， 翼面展开到位。其中， 点a， b， c位于一条直线上。

该小型旋转折叠翼方案的主要设计参数如下： F为高压气体产生的推力， 400 N； r为Oa距离， 0.045 m； J为翼面绕O点转动惯量， 0.242 kg·m2； m1为作动筒质量， 0.181 kg； l1为作动筒长度，0.121 m； m2为导杆质量， 0.026 kg； l2为导杆长度， 0.098 m； L为a点至C点的距离， 0.124 5 m； β为翼面初始角度， 45°。

2 小型旋转折叠翼展开运动方程

根据理论力学的拉格朗日方程可知， 完整推导小型旋转折叠翼展开运动方程需考虑所有运动部件的受力情况和动能变化， 推导过程较为繁琐， 得出的公式非常复杂。

对于本方案， 经计算可得导杆绕O点的转动惯量J2约为

通過数值解法， 在MATLAB中可以计算获得角度θ、 角速度θ·和角加速度θ¨分别与时间t的关系曲线， 具体计算步骤如下：

（1） 将角度θ∈[0， 90°]分成n个微小部分， 整个计算过程共有n+1个计算节点；

（2） 令第i（i∈[2， n+1]）个计算节点时的小型旋转折叠翼的角度为θi， 角速度为θ·i， 角加速度为θ¨i， 则通过第（i-1）部分的时间为Δti；

（3） 根据运动学知识可知以下关系：

（4） 将F， r， J， L和β代入式（6）～（7）求解。

3 基于ADAMS的小型旋转折叠翼动力学仿真

3.1 仿真模型的建立

通过Para solid（x_t）格式将UG中的小型旋转折叠翼三维模型精确地导入ADAMS中， 并默认继承原实体材质设置。

在翼面旋转轴与大地间设置转动副（Revolute）； 翼面与圆型立柱间设置固定副（Fixed）； 导杆与圆型立柱间设置圆柱副（Cylindrical）； 导杆与作动筒间设置平移副（Translational）； 作动筒与大地间设置转动副（Revolute）； 最后在导杆末端施加驱动力（Force）。

最终建立的小型旋转折叠翼展开仿真模型如图2所示。

3.2 不考虑摩擦， 空载时的动力学仿真分析

仿真时间设定为0.3 s， 仿真步长设定为3 000， 设置传感器， 使翼面转角大于90°时， 仿真结束。最后， 通过PECE预估校正算法， 进行动力学仿真分析。

将在ADAMS中测量得到的翼面转动中心处转动副的角度、 角速度和角加速度数据导入MATLAB， 与直接解算式（7）获得的数据， 分别通过曲线对比形式输出。

不考虑摩擦， 空载时角度、 角速度、 角加速度随时间的变化曲线如图3～5所示。

通过对比可知： 两种分析方法获取的不考虑摩擦情况下， 空载时小型旋转折叠翼的展开时间均为0.226 1 s； 两种分析方法获取的角度、 角速度和角加速度变化曲线高度重合， 证明在推导小型旋转折叠翼展开运动方程时忽略推杆质量等工程化处理方式的正确性， 同时证明了在ADAMS中建立的仿真模型的正确性。

3.3 满载时的动力学仿真模型

在该小型旋转折叠翼方案中， 翼面通过轴承实现角度转动， 其转动副的摩擦系数可选为0.05； 导杆与圆型立柱、 导杆与作动筒、 作动筒与大地间均为钢-钢润滑摩擦， 其摩擦系数均选为0.1。

翼面展开时承受的气动力与翼面展开角度密切相关， 但在缺乏气动力仿真和试验数据的情况下， 难以给出确定的气动力随展开角度的变化曲线， 假定翼面在整个展开过程中始终承受2 000 N的升力和666.7 N的阻力， 用以评估翼面展开的最长时间。

将气动力半分后分别施加于翼面的左右部分的几何中心，

确保施加重力的方向与翼面法向方向一致后， 进行动力学仿真分析。

在ADAMS中测量得到的满载时翼面转动中心转动副的角度、 角速度、 角加速度对时间的变化曲线如图6～8所示。

通过图6～8可知， 满载时小型旋转折叠翼的展开时间为0.245 1 s， 相比不考虑摩擦， 空载时的展开时间增加0.019 s， 增加率约8.4%； 满载与不考虑摩擦， 空载时的小型旋转折叠翼角度、 角速度和角加速度变化曲线的变化趋势基本一致。

满载时小型旋转折叠翼的机械效率为

式中： T为翼面的动能； P为推杆推力F所作的功。

根据图7可以看出， 翼面展开到位时角速度为801.2 （°）/s； 将各参数带入式（8）， 计算可得满载时小型旋转折叠翼的机械效率达到92.9%。

4 结 论

本文对一种摆动导杆驱动的小型旋转折叠翼方案进行研究。 应用动能定理， 得出了理想化模型的展开运动方程， 并通过MATLAB进行数值求解； 在UG中建立该方案的三维模型， 应用多体系统动力学理论在ADAMS中建立该方案的虚拟样机， 通过PECE预估校正算法， 仿真分析了动力学运动规律。通过对该方案的仿真分析可以得到如下结论：

（1） 在推导小型旋转折叠翼展开运动方程时， 可以根据翼面转动惯量和推杆等小质量机构间的比较， 进行忽略推杆质量等工程化处理方式， 能够有效简化推导过程和得出简洁的展开运动方程。

（2） 满载时， 该小型旋转折叠翼方案的展开时间为0.245 1 s， 满足在承受最大升力2 000 N和阻力666.7 N的情况下， 0.5 s内展开到位的设计要求； 其机械效率达到了92.9%， 机构的能量转化效率较高。

参考文献：

[1] 秦兵才， 文立华.小型折叠弹翼展开机构优化设计[J].弹箭与制导学报， 2009， 29（4）： 206-208.

Qin Bingcai， Wen Lihua. Optimization Design of Deploying Mechanism of a Small Folding Wing[J]. Journal of Projectiles， Rockers， Missiles and Guidance， 2009， 29（4）： 206-208.（in Chinese）

[2] 秦兵才， 文立华.接触分析在小型折叠弹翼仿真中的应用[J].航空兵器， 2012（3）： 11-13.

Qin Bingcai， Wen Lihua. Application of Contact Analysis to the Dynamic Simulation of Deploying Mechanism of a Small Folding-Wing[J]. Aero Weaponry， 2012（3）： 11-13.（in Chinese）

[3] 王明， 張美丽， 袁宴波.小型制导炸弹的质量质心计算方法[J].航空兵器， 2014（2）： 16-18.

Wang Ming， Zhang Meili， Yuan Yanbo. Computational Method of Small Guidance Bombs Mass and Centroid[J]. Aero Weaponry， 2014（2）： 16-18.（in Chinese）

[4] 李君山， 梁旭， 刘鹏， 等.一种小型轻质折叠弹翼展开解锁机构的设计及动力学仿真分析[J].航空兵器， 2013（4）： 7-9.

Li Junshan， Liang Xu， Liu Peng， et al. System Design and Dynamic Simulation Analysis of Release Mechanism for a Small-Light Folding Wing[J]. Aero Weaponry， 2013（4）： 7-9.（in Chinese）

[5] 李莉， 任茶仙， 张铎.折叠翼机构展开动力学仿真及优化[J].强度与环境， 2007， 34（1）： 17-21.

Li Li， Ren Chaxian， Zhang Duo. Dynamic Simulation and Optimization Design of Deployment of Folding-Wing[J]. Structure & Environment Engineering， 2007， 34（1）： 17-21.（in Chinese）

[6] 张玉石， 唐金兰， 任华， 等.燃气作动筒式折叠弹翼展开过程分析[J].固体火箭技术， 2010， 33（5）： 481-485.

Zhang Yushi， Tang Jinlan， Ren Hua， et al. Analysis of Mechanical Deployment System for Combustion-Gas-Actuated Folded Wings[J]. Journal of Solid Rocket Technology， 2010， 33（5）： 481-485.（in Chinese）

[7] 趙俊峰， 刘莉， 杨武， 等.折叠弹翼展开动力学仿真及优化[J].弹箭与制导学报， 2012， 32（2）： 155-157.

Zhao Junfeng， Liu Li， Yang Wu， et al. Dynamic Simulation and Optimization Design of Folding Wing Deployment[J]. Journal of Projectiles， Rockers， Missiles and Guidance， 2012， 32（2）： 155-157.（in Chinese）

[8] 张玲， 张世武， 孟建新.形状记忆合金驱动的折叠弹翼的结构设计[J]. 航空兵器， 2012（3）： 8-10.

Zhang Ling， Zhang Shiwu， Meng Jianxin. The Structural Design of Folding Wing Actuated by Shape Memory Alloys[J]. Aero Weaponry， 2012（3）： 8-10.（in Chinese）

[9] 雷歌， 邓飞， 刘权， 等.水下航行器折叠翼展开机构设计与动力学仿真[J].鱼雷技术， 2013， 21（2）： 81-85.

Lei Ge， Deng Fei， Liu Quan， et al. Design and Dynamic Simulation of Folding Wing Expansion Mechanism for Underwater Vehicle[J]. Torpedo Technology， 2013， 21（2）： 81-85.（in Chinese）

[10] 赵俊峰， 刘莉.折叠弹翼展开的刚柔耦合动力学分析[J].弹箭与制导学报， 2011， 31（5）： 141-144.

Zhao Junfeng， Liu li. Flex-Rigid Coupling Dynamics Analysis of Folding Wing Deployment[J]. Journal of Projectiles， Rockers， Missiles and Guidance， 2011， 31（5）： 141-144.（in Chinese）

[11] 崔二巍， 于存贵， 李猛， 等.某导弹折叠弹翼展开过程的仿真分析[J].兵工自动化， 2013， 32（12）： 12-14.

Cui Erwei， Yu Cungui， Li Meng， et al. Simulation Ana-lysis of a Missile Folding Wing Deployment Process[J]. Ordnance Industry Automation， 2013， 32（12）： 12-14.（in Chinese）

[12] 胡明， 章斌， 陈文华， 等.“一字型”折叠翼展开试验与仿真验证分析[J].中国机械工程， 2015， 26（13）： 1801-1805.

Hu Ming， Zhang Bin， Chen Wenhua， et al. Expand Performance and Simulation Verification of Line-styled Folding-Wing[J]. China Mechanical Engineering， 2015， 26（13）： 1801-1805.（in Chinese）

[13] 和兴锁. 理论力学[M].北京： 科学出版社， 2001.

He Xingsuo. Theoretical Mechanics[M]. Beijing： Science Press， 2001. （in Chinese）

[14] 刘慧颖.MATLAB R2007 基础教程[M].北京： 清华大学出版社， 2016.

Liu Huiying. Basic Tutorials of MATLAB R2007[M]. Beijing： Tsinghua University Press， 2016.（in Chinese）

[15] 陈德民， 槐创锋， 张克涛， 等. 精通ADAMS2005/2007虚拟样机技术[M].北京： 化学工业出版社， 2010.

Chen Demin， Huai Chuangfeng， Zhang Ketao， et al. Proficient in ADAMS2005/2007 Virtual Prototyping Technology[M]. Beijing： Chemical Industry Press， 2010.（in Chinese）

Dynamics Simulation of Small Rotating Folding Wing Driven by Swing Rod

Wang Ming

（China Airborne Missile Academy， Luoyang 471009， China）

Abstract： The rotating folding wing configuration can significantly increase the flying distance of small guided bombs. In order to verify the unfolding performance of rotating folding wing， a scheme of small rotating folding wing driven by swing rod is studied. By applying the kinetic energy theorem of theoretical mechanics， the motion equation of idealized model is obtained， and numerical calculation is carried out through MATLAB. By applying the multi-body system dynamics theory， the schemes virtual prototype is established in ADAMS. Through PECE forecast correction algorithm， the dynamic motion rules is analyzed by simulation. The simulation results show that the motion rules of small rotating folding wing obtained by the two analytical methods are the same. In full-load case， the unfolding time of the scheme meet the designs requirement.

Key words： small rotating folding wing； dynamics simulation； MATLAB； ADAMS