GNSS可用星数对GNSS/SINS紧组合系统性能影响分析
2018-01-24孙兆妍王新龙李群生王盾
孙兆妍+王新龙+李群生+王盾


摘 要: 定量分析了GNSS可用星数对GNSS/SINS紧组合导航系统性能的影响, 建立了一种紧组合系统可观测性分析模型, 推导了紧组合系统的可观测性矩阵, 并针对不同GNSS可用星数的情况给出了GNSS/SINS紧组合导航系统的可观测性理论分析结果以及各状态量的可观测度和导航解算性能。 仿真结果表明: 当有4颗及以上可用星时, 由于GNSS/SINS紧组合导航系统完全可观, 因此可获得高精度的导航信息; 而当可用星数短时衰减为3颗时, 且短时间内时钟误差较为稳定, 则短期内GNSS/SINS紧组合导航系统仍可提供较高精度的导航信息; 当仅有1颗或2颗可用星时, 由于量测信息严重不足, 导致组合系统状态量的可观测度大幅下降, 使得组合系统的导航精度明显降低。
关键词: 导航模式; GNSS/SINS紧组合; 可见星数; 可观测性分析
中图分类号: TJ765; V249.32+ 8 文献标识码: A文章编号: 1673-5048(2017)06-0032-09[SQ0]
0 引 言
捷联式惯性导航系统(Strapdown Inertial Navigation System, SINS)自主性强, 导航信息完整, 但导航误差随时间积累; 全球定位卫星系统(Global Navigation Satellite System, GNSS)具有较高的定位精度, 且无累积误差, 但容易受到遮蔽和干扰[1]。 因此SINS与GNSS具有极强的功能互补性, 将二者相结合, 可以充分发挥子系统各自的优点, 使组合导航系统具有高精度、 低成本、 抗干扰性强等优点[2]。
GNSS/SINS松組合和紧组合是目前应用最为广泛的GNSS/SINS组合导航模式[3]。 松组合是一种低水平的组合模式, 组合滤波器直接利用GNSS和SINS解算得到的载体位置/速度之差作为量测量, 估计并校正SINS的器件误差。 这种组合方式具有结构简单、 容易实现等优点。 但由于GNSS和SINS需要独立解算载体的位置/速度信息, 因此必须保证GNSS可用星不少于4颗, 而GNSS信号易受遮挡或干扰, 复杂环境中难以保证足够的GNSS可用星数, 从而影响了松组合系统的稳定性; 另外, GNSS解算与组合滤波构成了滤波级联, 这将导致误差相关[4], 进一步影响松组合导航解算的精度。 而紧组合方式将GNSS和SINS提供的伪距/伪距率作为量测信息通过组合导航滤波器进行导航参数的估计[5], GNSS不再需要独立解算载体位置/速度信息, 不仅避免了松组合滤波级联导致的误差相关性问题, 而且克服了GNSS至少4颗可用星的限制。 因此, 相比于松组合, GNSS/SINS紧组合导航系统具有更高的导航精度, 系统的可靠性也得到了大幅改善[6-7]。 由于GNSS/SINS紧组合导航系统在复杂环境下表现出的优异性能, 其已被广泛运用到工程实践中, 尤其是航空航天等军事领域。
虽然GNSS/SINS紧组合导航系统能够在可见星不足的情况下维持导航能力, 但是工程实践表明, 可见星的缺失将会显著影响紧组合系统的导航性能。 因此, 本文基于PWCS可观测性分析理论, 定量分析了可用星数对GNSS/SINS紧组合系统导航性能的影响。
1 GNSS/SINS紧组合系统模型
1.1 组合系统结构
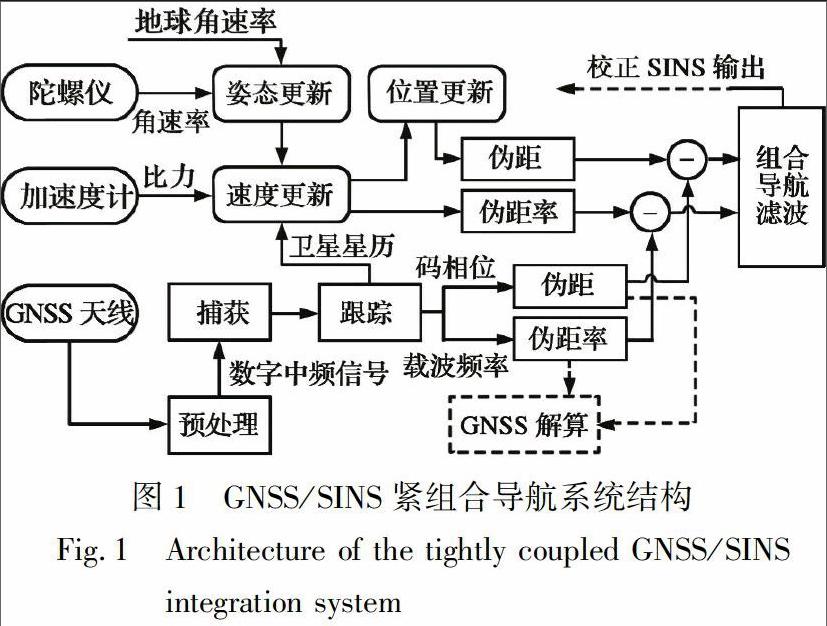
GNSS/SINS紧组合导航系统的结构[8]如图1所示。 GNSS分系统中, 接收机通过天线接收GNSS信号, 并对信号进行预处理(包括预滤波、 下变频、 模数转换等)得到数字中频信号; 然后捕获信号获得粗略的捕获参数(码相位和载波频率); 进一步, 根据粗略的捕获参数, 信号跟踪环不断缩小本地信号与接收信号间的频率误差, 直至达到高精度同步; 最后将跟踪获取的码相位和载波频率转换为伪距和伪距率信息(GNSS部分)。 SINS分系统利用陀螺仪和加速度计输出的角速率和比力信息, 根据SINS力学编排方程, 不断更新捷联姿态阵, 从而实时解算载体的位置和速度; 得到位置、 速度信息后, 结合GNSS信号跟踪剥离得到的卫星星历, 计算SINS与导航卫星间的视线相对距离/速度, 即SINS部分的伪距和伪距率信息。 最终, 将SINS与GNSS的伪距和伪距率之差作为量测量, 组合导航滤波器估计载体的导航参数, 并实时校正SINS的器件误差。
由此可以看出, 紧组合与松组合的主要区别在于: 松组合中, GNSS需要独立解算载体的位置速度(如图1中虚线框所示), 这就要求至少4颗可用星; 而紧组合直接采用GNSS跟踪获得的伪距和伪距率信息, 此时GNSS不再需要具备独立解算载体位置/速度的能力, 因此当可用星不足时, 组合导航滤波器仍然能够工作, 但是由于量测量的缺失, 将会导致滤波精度的下降。
1.2 组合系统模型
(1)状态方程
为了简化可观测性分析, 并充分有效估计载体的导航参数, 这里以地心惯性系(Earth-Centered Inertial, ECI)为基准坐标系, 选取GNSS/SINS紧组合导航系统的估计状态量为[9]
其中: ψi, δP·i和δPi分别为SINS的平台失准角、 速度误差、 位置误差; tb和td分别表示GNSS的时钟偏差和时钟漂移; 上标i表示惯性系。 在惯性系下, SINS和GNSS各误差状态的传播方程可以表示为
式中: 上标b表示本体坐标系; Γi=giPi; gi为重力加速度矢量(惯性系); ai表示加速度计输出的比力(惯性系); δab为加速度计输出比力误差(本体系); δωbib为陀螺仪输出角速率误差(本体系); δgi表示重力加速度模型偏差(惯性系); δtb和δtd分别为时钟偏差和时钟漂移中的噪声; β为时钟漂移系数; Cib为本体系至惯性系的姿态转换阵。 则根据式(1)~(2)可知, GNSS/SINS紧组合导航系统的状态方程可以表示为
其中: n表示可用星数; Ln×3表示载体至GNSS导航卫星的视线方向(Line of Sight, LOS)矩阵。
2 不同可用星数对组合系统可观测性的影响分析
2.1 可观测性分析方法
Kalman滤波是GNSS/SINS紧组合导航系统中数据融合的核心算法, 其稳定性主要依赖于导航系统各状态量的可观测能力, 因此分析系统可观测性是检测系统是否有效可靠的必要工作[10-11]。 由于GNSS/SINS紧组合导航系统的时变性, 不能直接使用时不变系统的可观测性判据[12], 而针对时变系统的分段线性定常系统(Piece Wise Constant System, PWCS)可观测性分析方法[13-14]仅能给出系统状态可观性的定性结果, 无法给出每个系统状态的可观测程度(即可观测度)[15]。 故针对GNSS/SINS紧组合导航系统, 这里采用PWCS可观测性分析方法[16]和基于奇异值分解(Singular Value Decomposition, SVD)可观测度相结合的分析方法对其的可观测性进行定量分析。
根据系统的动态特征, 如果在设定时间区间内, 线性时变系统的系数矩阵变化量可以忽略不计, 那么该时间区间内可以把时变系统当作定常系统处理, 这样的系统称为PWCS。 针对GNSS/SINS紧组合导航系统, 取一个较短时间段(认为该时间段内系统具有时不变特性), 并分为时间间隔为Δt的连续N个区间, 其中Δt为紧组合导航系统的更新历元间隔, 则该时间段内系统模型可描述为离散线性的PWCS模型, 表示如下:
式中: Q为该时间段内系统的可观测矩阵, 而初始状态X(1)的估计效果将取决于系统可观测矩阵Q的特性, 可观测状态量的个数与Q的秩保持一致, 若Q满秩, 则表明该系统完全可观。
SVD可观测度分析方法是将可观测矩阵Q进一步分解为
其中: ai=1σi代表这个椭球的主半轴长度。 由于观测量是确定已知的, 如果奇异值σi越大, 那么主半轴长度就越小, 所形成的椭球空间就越狭窄, 最终X(1)的估计效果就越好。 反之, 如果奇异值越小, 会导致椭球体积变大, 此时X(1)的估计效果将会变差。 因此, 状态量的可观测度可以由奇异值的大小反映。
2.2 可观测性分析模型
为了建立GNSS/SINS紧组合导航系统的可观测性分析模型, 重写其量测方程为
考虑单个时间段内系统的可观测性, 根据式(18), 建立GNSS/SINS紧组合导航系统的PWCS可观测性矩阵Q模型如下:
将H和F代入Q中得到
GNSS/SINS紧组合导航系统测量误差来源为三轴陀螺仪和三轴加速度计的6项误差以及GNSS时钟的2项误差(其他如接收机热噪声、 多径干扰等认为是不可建模的量测噪声), 即紧组合导航系统所需解算的完全独立状态量为8项, 如图2中所示的八维坐标系。 那么, 当GNSS/SINS紧组合有4颗可用星时, 经过一次量测, 能够得到包括伪距和伪距率的8个量测信息, 表现为可观测性矩阵Q的秩为8, 如图2中虚线箭头所示, 并且该量测信息与八维坐标轴间具有线性关系, 因此此时紧组合系统具有观测8项完全独立状态量的能力。 由此可知, 当可用星不少于4颗时, GNSS/SINS紧组合导航系统是完全可观的。
若认为相邻历元内载体与导航卫星间的相对运动非常小, 即LOS向量的变化可忽略, 由式(26)可以看出, Q中第2n+1行与第2n+2行完全一致。 则若可用星数下降为3颗, 此时一次量测得到的可观测性矩阵Q秩为6, 不满足8项完全独立状态量的可观测性要求; 两次量测后, Q秩为9。 因此, 为了获得8状态的观测能力, 至少要保证两次观测。 同理, 若可用星数为2, 则需要4次量测才能使得8状态系统完全可观; 当可用星数为1, 则8状态系统完全可观所需量测数增至6次。
但是, 由于載体和导航卫星均处于运动状态, 因此每次量测历元所对应的H阵和F阵不断变化, 即所需估计的误差状态也是动态变化的, 若分析可观测性时选取的量测时间段过长, 则不能满足PWCS可观测性分析方法对系统时不变的要求, 即可观测性分析失效。 因此当可用星数仅为1颗或2颗时, 4次或6次的量测历元内, GNSS/SINS紧组合导航系统的时不变假设难以成立, 即增加观测历元并不能改善状态量的可观测性。
3 紧组合系统性能仿真验证
3.1 仿真条件
采用东北天坐标系作为导航系, 载体初始位置位于北纬40°, 东经116°, 向北飞行, 初始北向速度为250 m/s, 载体总飞行时间为70 s, 并在70 s内完成匀速、 爬升、 加速、 转弯、 减速、 俯冲等机动(加速度均小于1 m/s)。
GNSS/SINS紧组合导航系统中, 采用的惯性器件误差为陀螺仪常值漂移为0.1 (°)/h, 一阶马尔科夫过程白噪声方差为0.01 ((°)/h)2; 加速度计零偏为100 mg。 GNSS接收机捕获和跟踪灵敏度设置为32 dB-Hz, 并且导航卫星的可见仰角范围为10°~80°。 SINS解算频率为100 Hz, 信号跟踪频率为100 Hz, 组合导航解算频率为10 Hz。
为了分析GNSS/SINS紧组合导航系统全部20个待估计状态的可观测性, 采用PWCS方法, 选取分析时间段(假设该时间段内系统具有时不变性)为10 s, 为了清晰简洁表示各状态量, 对20个状态量进行编号, 如表1所示。
3.2 仿真结果分析
(1) 4颗可用星情况可观测性分析
当有4颗可用星时, 分析GNSS/SINS紧组合导航系统的可观测性, 其结果如图3~7所示。 从图3(a)~(b)可以看出, 可观测性最好的状态量为纬度和经度, 其原因在于: GNSS星座采用中圆地球轨道, 因此对于地面或低空载体, 载体与导航卫星之间的相对运动主要体现为经度和纬度的变化, 并且紧组合系统的量测量伪距(率)与经度/纬度(变化量)有着直接的关系。
另外, 由图4(c)~(d)以及图5(a)~(b)可知, 东向和北向陀螺仪的常值漂移(状态10和状态11)、 一次项系数(状态13和状态
14)以及东向和北向失准角的观测性也较好。 并且, 状态10与状态13, 以及状态11与状态14之
间可观测性基本保持一致, 表明在GNSS/SINS紧组合导航系统中, 组合导航滤波器对陀螺仪常值漂移和一次项系数的估计具有强相关性。
分析图5(c)~(d)以及图6(a)~(b)可知, 东向/北向速度和时钟偏差/漂移均可观测, 但是可观测度较低, 原因为虽然载体的速度以及时钟状态量能够直接由量测量反映(钟偏对应伪距, 速度和钟漂对应伪距率), 但是在较短的观测时间段内, 载体与导航卫星间的相对速度变化较小, 且时钟偏差/漂移也相对稳定。
由图6(c)~(d)和图7可知, 对应标出状态量(天向失准角、 天向速度、 高度以及陀螺/加速度误差)的可观测性均较差。 由于载体和导航卫星间相对高度变化较小, 因此难以准确估计天向失准角、 天向速度以及高度状态量。 此外, 由于GNSS/SINS紧组合只能提供伪距和伪距率量测量(分别对应位置和速度状态), 而缺失与姿态相关的量测量, 因此不能直接反映陀螺和加速度的误差, 导致陀螺/加速度误差可观测性较差。
由图3(c)~(d)可知东向和北向陀螺仪误差可观测性较好, 而图6(b)~(c)显示其可观测性较差。 可见, 东向和北向陀螺仪误差是可观测的, 但其可观测度不稳定, 受到载体机动方式的影响。
(2) 不同可用星数情况下可观测度对比
对比不同可用星数状态下GNSS/SINS紧组合导航系统的可观测性, 其可观测状态及对应的奇异值见表2。 从表2中可以看出, 随着可用星数的减少, 可观测状态数不断下降。 尤其当可用星仅为1颗时, 只有4个状态可观测, 而由于实验中采用的载体向北飞行, 因此可观测性较好的状态分别为纬度、 东向陀螺误差以及东向失准角。
同时, 对于GNSS/SINS紧组合导航系统, 若载体处于近地面或低空飞行, 则载体与导航卫星的相对运动主要体现为经纬度的变化, 因此即使可用星数小于4颗, 其经度、 纬度、 东向/北向陀螺误差以及东向/北向失准角的可观测性仍然较好。
(3) 不同可用星数情况下导航解算性能对比
给定GNSS/SINS紧组合导航系统的初始状态为4颗可用星, 40~50 s时, 可用星数衰减为3颗或2颗或1颗, 50 s后恢复4颗可用星, 对应的导航解算位置和速度误差分别见图8~13, 误差RMS以及重新收敛时间见表3。 由图8~9可知, 由于时钟误差基本保持稳定, 短时间内可作为已知量, 因此当可用星衰减为3颗时, GNSS/SINS紧组合导航系统的位置和速度估计精度仍然较高, 根据表3显示位置误差RMS约为9.8 m, 速度误差RMS约为0.05 m/s, 且可用星数恢复至4颗后, 重新收敛时间小于1 s。
图10~12显示, 当40~50 s可用星数仅为2颗或1颗时, 即使认为时钟误差为已知量, 量测量个数仍然不足以解算位置/速度状态, 使得紧组合系统的解算误差激增, 从表3中可以看出位置误差RMS大幅增长至30 m, 速度误差RMS超过9 m/s。
并且, 重新恢复4颗可用星后, 导航解算收敛速度较慢, 收敛时间约为10 s。
根据以上分析可知, 若可用星数出现短时衰落, 无法提供足够的量测量以解算载体的四维状态, GNSS/SINS紧组合导航系统仍然能够正常工作, 尤其当有三信号锁定时, 可以保持短时较高的导航精度。 但是若可见星只有1颗或2颗, 则由于量测信息不足, 将会导致紧组合的導航精度大幅下降。
4 结 论
在遮挡或干扰环境中, GNSS信号容易受到影响, 导致GNSS/SINS紧组合导航系统中的可用星数发生波动, 影响系统的导航性能。 本文定量分析了GNSS可用星数对GNSS/SINS紧组合导航系统性能的影响, 据此进行了仿真验证与分析, 得到结论如下:
(1) 采用伪距和伪距率作为量测量的GNSS/SINS紧组合导航系统, 若至少有4颗可用星, 则系统完全可观, 并且经度/纬度、 东向/北向陀螺仪误差以及东向/北向失准角的可观测度较好。 若可用星数小于4颗, 由于量测量的缺失, 不仅导致紧组合系统的可观测状态量数目减少, 而且可观测度也大幅下降。
(2) 若可用星数短时衰减为3颗, 鉴于短时间内时钟误差较为稳定, 因此缺少一维量测量时, GNSS/SINS紧组合导航系统仍然能够保证载体三维位置和速度的解算, 并且在短期内维持较高的导航精度。
(3) 若仅有1颗或2颗可用星, 紧组合导航系统中的组合滤波器虽然能够进行估计解算, 但由于量测信息的严重不足, 其估计精度将受到较大的影响, 并且恢复4颗可用星后重新收敛速度较慢, 即1颗或2颗可用星情况下, 紧组合系统的导航性能将大幅下降。
参考文献:
[1] Spilker J J, Jr. Fundamentals of Signal Tracking Theory[J]. Global Positioning System: Theory and Applications, 1996, 1: 245-328.
[2] Schmidt G T. INS/GPS Technology Trends[M]. Massachusetts Inst of Tech Lexington, MA, 2010.
[3] 王君帅, 王新龙. SINS/GPS紧组合与松组合导航系统性能仿真分析[J]. 航空兵器, 2013(2): 14-19.
Wang Junshuai, Wang Xinlong. Simulation and Analysis of SINS/GPS Tightly Coupled and Loosely Coupled Integrated Navigation System[J]. Aero Weaponry, 2013(2): 14-19.(in Chinese)
[4] 孫兆妍, 王新龙. SINS/GPS 松组合与紧组合导航系统抗干扰性能比较与验证[J]. 航空兵器, 2014(4): 31-35.
Sun Zhaoyan, Wang Xinlong. Comparison and Demonstration of Interference Immunity of SINS/GPS Loosely Coupled and Tightly Coupled Integrated Navigation System[J]. Aero Weaponry, 2014(4): 31-35.(in Chinese)
[5] Crane R, Alexander S, Beser J, et al. System and Method for Advanced Tight Coupling of GPS and Inertial Navigation Sensors: US, 7274504[P]. 2007.
[6] Miller I, Campbell M. Sensitivity Analysis of a Tightly-Coupled GPS/INS System for Autonomous Navigation[J]. IEEE Transactions on Aerospace & Electronic Systems, 2012, 48(2): 1115-1135.
[7] Alexander S B. Tight Coupling of GPS and Navigation Estimates with Reducer or Eliminated Inertial Measurement Unit Data: US, 7916070[P]. 2011.
[8] Knight D T. Achieving Modularity with Tightly-Coupled GPS/INS[C]∥IEEE Plans 92 Position Location and Navigation Symposium Record, 1992: 426-432.
[9] Budiyono A. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems[M]. Artech House, 2013.
[10] Hong S, Lee M H, Chun H H, et al. Observability of Error States in GPS/INS Integration[J]. IEEE Transactions on Vehicular Technology, 2005, 54(2): 731-743.
[11] Katona G, Burgos-Vargas R. Investigating Observability Properties from Data in Nonlinear Dynamics.[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2011, 83(2): 1509-1520.
[12] Hong S, Lee M H, Rios J, et al. Observability Analysis of GPS Aided INS[C]∥Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2000.
[13] Goshen-Meskin D, Bar-Itzhack I Y. Observability Analysis of Piece-Wise Constant System-PartⅠ: Theory[J]. IEEE Transaction on Aerospace and Electronic Systems, 1992, 28(4): 1056-1067.
[14] Goshen-Meskin D, Bar-Itzhack I Y. Observability Analysis of Piece-Wise Constant System-PartⅡ: Application to Inertial Navigation In-Flight Alignment[J].IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(4): 1068-1075.
[15] Kong Xingwei, Dong Jingxin, Ji Qingchang,et al. INS Observable Degree Analysis Method Based on PWCS[J]. Journal of Chinese Inertial Technology, 2011, 19(6): 631-792.
[16] Kong Xingwei, Guo Meifeng, Dong Jingxin. An Improved PWCS Approach on Observability Analysis of Linear Time-Varying System[C]∥Control and Decision Conference, 2009: 816-820.
Performance Analysis of the Tightly Coupled GNSS/SINS Integrated System with Different Numbers of Available Satellites
Sun Zhaoyan1, Wang Xinlong1, Li Qunsheng2, Wang Dun3
(1. School of Astronautics, Beihang University, Beijing 100191, China;
2. School of Instrumentation Science and Opto-Electronics Engineering, Beihang University, Beijing 100191, China;3. Space Star Technology co., LTD., Beijing 100086, China)
Abstract: In order to analyze the performance of the tightly coupled GNSS/SINS integrated system under conditions of different available satellite numbers, an observability model for the tightly coupled system is established and its observability matrices are derived. Considering the conditions of different available satellite numbers, the observability analysis of the tightly coupled system, the observability level of system states and its navigation performance are presented. The simulation results show that when there are four or more available satellites, as the tightly coupled system is completely observable, accurate navigation could be achieved; when the available satellite number reduces to three during a short time and the clock error is stable, the tightly coupled system could still provide relatively accurate navigation information; when there are only one or two available satellites, the state observability level sharply drops due to the serious shortage of measurement information, which resulting the navigation performance declined.
Key words: navigation mode; tightly coupled GNSS/SINS integrated system; numbers of available satellites; observability analysis
