Nonlinear Waves on Localized and Periodic Backgrounds with Time-Space Modulation∗

Mei-Kun Liu(刘美坤),Zhan-Ying Yang(杨战营),,† and Wen-Li Yang(杨文力)School of Physics,Northwest University,Xi’an 710069,China

2Shannxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710069,China

3Institute of Modern Physics,Northwest University,Xi’an 710069,China

1 Introduction

Nonlinear waves on a plane-wave background become a subject of intense research in nonlinear physics,ranging from nonlinear optics,Bose–Einstein Condensates(BECs),magnetics,plasmas,super fluid,et al.[1−9]These localized waves evolving on a nonvanishing background exactly describe the dynamical growth of perturbations on a plane-wave related to the nonlinear modulation instability.This includes Akhmediev breathers,[10]Kuznetsov–Ma breathers,[11]and the Peregrine(rational)rogue waves,[12]which are now considered the simplest models to describe the growth and decay of isolated steep wave events,i.e.,rogue waves,in nonlinear dispersive systems.[13−14]Especially,significant progress has been made on the experimental verification of these unique nonlinear structures in fiber optics,[15−17]in water tank,[18]and in plasma systems.[19]On the other hand,the utility of these waves based on their special properties in generating high-quality pulse trains,[20]high-power pulses,[21]breatherlike solitons,[22]nonlinear Talbot effects,[23]and the Peregrine comb[24]has been revealed.

However,in practice,the simple solution on an ideal plane-wave background may be not as adequately representative of reality as commonly thought.Indeed,a plane wave is an in finite-width background that corresponds to extreme high background powers.Therefore,from the application and technical points of view,the study on nonlinear waves on a finitewidth background is of practical importance.Recently,the excitation of Peregrine rogue waves on Gaussian and Sech-shaped backgrounds has been investigated.[25−26]It has been shown that the characteristics of Peregrine rogue waves are maintained.However,the breathers,which are more general waves,have not been studied on a finitewidth background so far.On the other hand,a plane wave,upon which these solutions are built,is simply a limiting cases of the periodic waves.From a statistical perspective,these periodic oscillations appear far more common in the ocean than any idealised background with constant amplitude.In fact,in the experiment of water tank,the rogue waves are excited on a regular wave train.[27]It is also not uncommon for an optical periodic wave to appear in a fiber as a regular train of solitonic pulses.[28]Indeed,recent experiments in optical fiber demonstrated the propagation of periodic waves in a stable manner.[29]

In this paper,we study the general nonlinear waves generation on finitewidth(localized)and periodic backgrounds.We present a general family of analytical solutions for the generalized nonlinear Schrödinger equation with time-space modulation via the method of a combination of the Darboux transformation and similarity transformation. Nonlinear waves on different localized and periodic backgrounds depending on the corresponding nonlinearity modulations are obtained.In particular,we demonstrate the existence and property of localized modes on a double-periodic background under a special designed optical lattice potential.

2 Model and Analytical Solutions

We study nonlinear waves on localized and periodic backgrounds by a generalized nonlinear Schrödinger equation(NLSE)with time-space modulation variable coeff-cients,which is given by

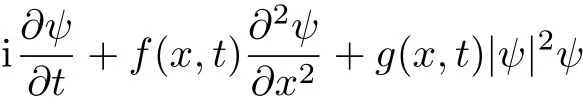
whereψ(x,t)is a complex function,xrepresents the distribution direction andtrepresents the evolution direction.f(x,t)is the dispersion coeffcient andg(x,t)is the nonlinearity management parameter.V(x,t)denotes the external potential andγ(x,t)is the gain(or loss)term.In fact,model(1)is a generalized nonautonomous NLSE given in Ref.[30].The integrability of the nonautonomous NLSE have been studied in Ref.[31].The properties of solutions of two kinds of non-isospectral nonautonomous NLSE have been discussed in Ref.[32].The dynamics of standard solitons(i.e.,bright and dark structures)have been studied in Ref.[33].In particular,dynamics of rogue waves and breathers in Eq.(1)have been studied recently in Refs.[34–38].If these variable coeffcients are functions only related tot,we can present rogue wave and breathers in BECs,which are similar to the results in Refs.[35–36].Moreover,with some higher-order effects added in Eq.(1),the rogue wave management in a fiber is studied.[37]If these variable coeffcients are functions only related tox,the rogue wave management has been studied in Ref.[38].On the other hand,one should note that optical rogue waves in the generalized higher-order NLSE with time-space modulation have been studied in Ref.[39].Moreover,the standard solitons in Eq.(1)with quintic nonlinearity have been demonstrated in Ref.[40].In the following,we will present the exact general solution,which describes rogue waves and breathers on different backgrounds.

We assume that the form of a solution of Eq.(1)as follows

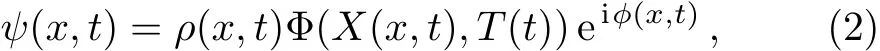
whereρ(x,t),ϕ(x,t),X(x,t),T(t)are real variable functions.ρ(x,t)andϕ(x,t)are amplitude and phase of the nonlinear localized waves,respectively.Φ(X,T)is the solution of the NLSE

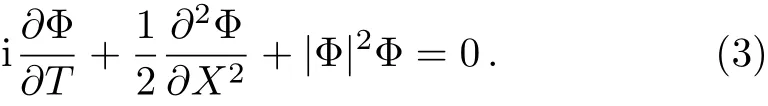
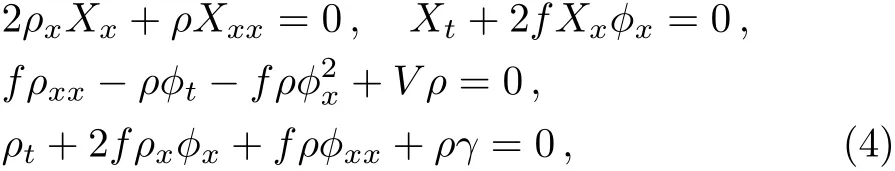
where the contained parameters satisfy the constraint condition

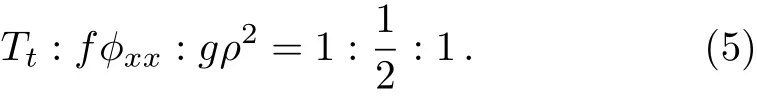
The subscripts denote the partial derivative respect toxort.From the partial differential equations and the con-straint conditions,we can obtain the amplitudeρ(x,t)=√the phasethe dispersion coeffcientf(x,t)=(1/2)aα−2F−2,the gain(or loss)term

hereais a function that depends ontandT0is a real constant.Furthermore,the expression of the potential is given

with

Using similarity transformation,we can obtain the exact solution of Eq.(1),

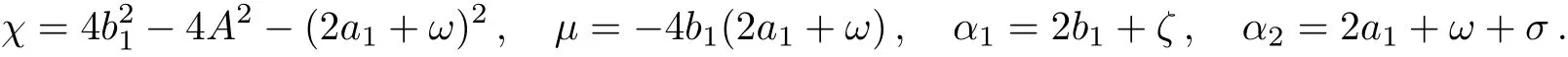
Aandωrepresent the amplitude and frequency of the background,respectively.b1anda1are arbitrary constant parameters.

The breather is a localized solution with temporally and/or spatially periodic structures having constant background exhibiting internal oscillations and bound states of nonlinear wave packets.[41]The unified solution(7)describes abundant different types nonlinear localized waves with different parameters,including Kuznetsov–Ma(KM)breather,Akhmediev breather(AB)and rogue wave.

In the case ofν=0,andσ=0,the general breather becomes to KM breather,which is periodic in the evolution direction and localized in the distribution direction.The form of the KM breather can be given by

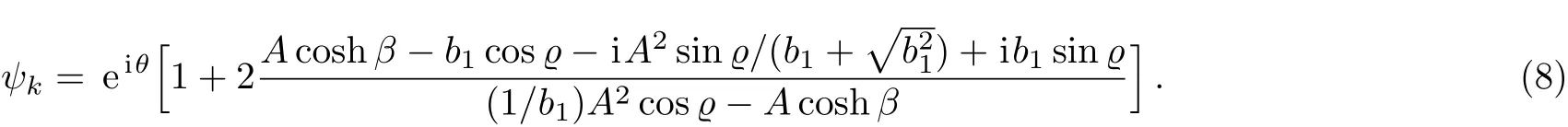
The rogue wave can be obtained by taking the limitsandσ=0.In this case,Eq.(7)reduces to the following form

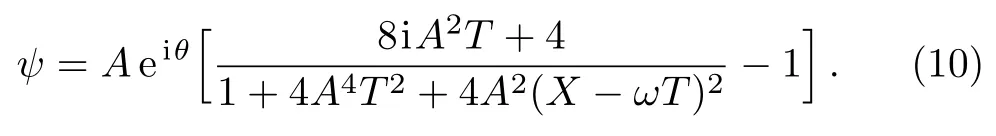
3 Nonlinear Waves on Localized Backgrounds

Most of the theoretical studies focus on the rogue waveand breatherssolutionson plane-wavebackgrounds.[2−5,42−46]In practice,the ideal plane-wave background are non-existent.Therefore,from the application and technical points of view,the study on nonlinear waves on localized background is of practical importance.We have nonlinear term manipulation to achieve the purpose of controlling the nonlinear wave.The nonlinearity coeffcient can be controlled by suitably managing the parametersα(t),F(ϖ),anda(t),we are explaining it by considering the following two kinds of situations in below.

3.1 The Evolution-Direction Localized Background

For the evolution direction localized background,we choose the nonlinearity coeffcient as

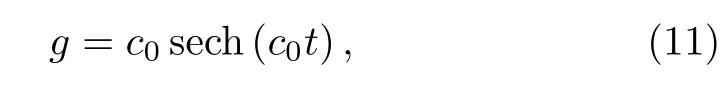
wherec0is an arbitrarily constant.In this case,the dispersion,gain,and potential should be chosen asf=const.γ= −at/2a−αtx/α,V(x,t)=whereα(t)=c0sech(c0t),a(t)=α2.

In Fig.1,we plot the rogue wave and breathers on the evolution direction localized background,here the potential is the space-quadratic potential in Fig.1(e).Whent→0,the amplitude of background gradually increases in the evolution direction.As show in Fig.1(a),rogue wave becomes more and more localized in the evolution direction.At this time,the AB and the general breather have stretching occurs in distribution direction,which show in Figs.1(b)and 1(c).Unlike the AB and the general breather,the KM breather is localized in bothtandx,the periodically of the KM breather in the evolution direction completely destroyed(see the wave in Fig.1(d)).Interestingly,as increasing thec0,the background get more localized in the evolution direction and the amplitude of the nonlinear waves are increased.

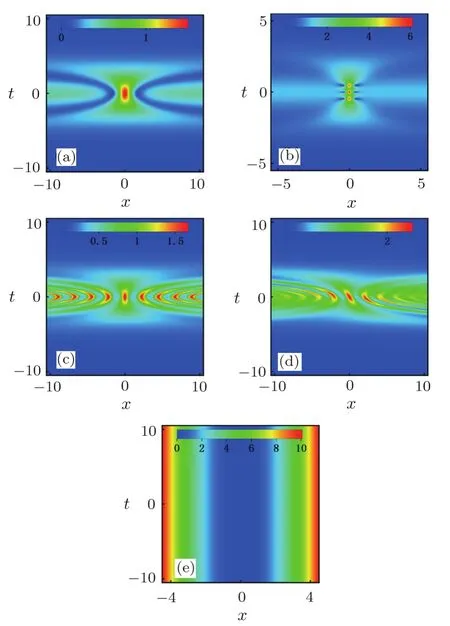
Fig.1 (Color online)Density plot of RW and breathers|ψ|on the evolution direction localized background.(a)Rogue wave with c0=1,A=1/2,ω=0.(b)The Kuznetsov–Ma breather with c0=3/2,b1=2,A=1,ω=0. (c)The Akhmediev breather with c0=1,A=3/2,b1=1/2,ω=0.(d)The general breather with c0=1,b1=3/2,A=1/2,ω=0,a1=1/2.(e)The potential with c0=1.Other parameter is T0=0.

3.2 The Distribution-Direction Localized Background

For the distribution direction localized background,we choose the nonlinear coeffcient

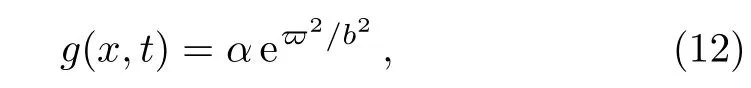
whereϖ=αx,and

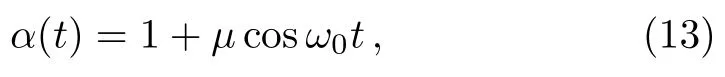
withµ∈ (−1,1),ω0∈R.Remarkably,depending on the different choices ofµ,there are two cases to consider as follows:

(i)Whenµ=0,the nonlinearity coeffcient

In this case,the dispersion,gain,and potential should be selected as

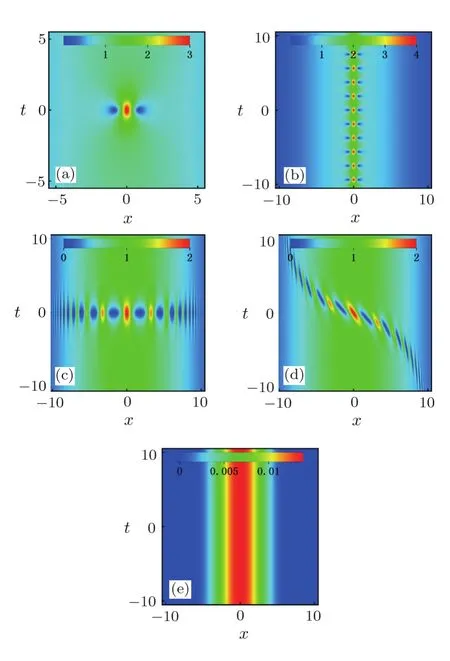
Fig.2 (Color online)Density plot of rogue wave and breathers|ψ|on distribution direction localized background.(a)Evolution of rogue wave solution.(b)The Kuznetsov–Ma breather with b1=3/2.(c)The Akhmediev breather with b1=1/2.(d)The general breather with b1=3/2,a1=1/2.(e)Plot of the potential given with b=6.Others are A=1,ω=0,b=6,T0=0.

Figures 2(a),2(b),2(c),and 2(d)demonstrate the intensity profiles of rogue wave,KM breather,AB and the general breather on the distribution direction localized background,respectively.The potential is like a potential barrier,which shows in Fig.2(e).Figure 2(a)shows the evolution of the rogue wave,which is localized in both two spatial directions on distribution direction localized background.It has been demonstrated that the characteristics of rogue wave(a high amplitude and double localization)are maintained on distribution direction localized background.Figure 2(b)shows that KM breather is periodic intand localized inxon distribution direction localized background.It should note that the characteristics of the KM breather on the distribution direction localized background is similar to the one on the plan wave background.Figures 2(c)and 2(d)show the amplitude of AB and general breather decrease with the amplitude of background decreasing,which fully disappears atx→±∞.

(ii)Ifµ/=0,the nonlinearity coeffcient

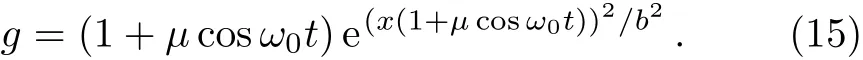
The external potential is a complex function of trigonometric function and exponential function.The dispersion management and the gain(or loss)term parameterand

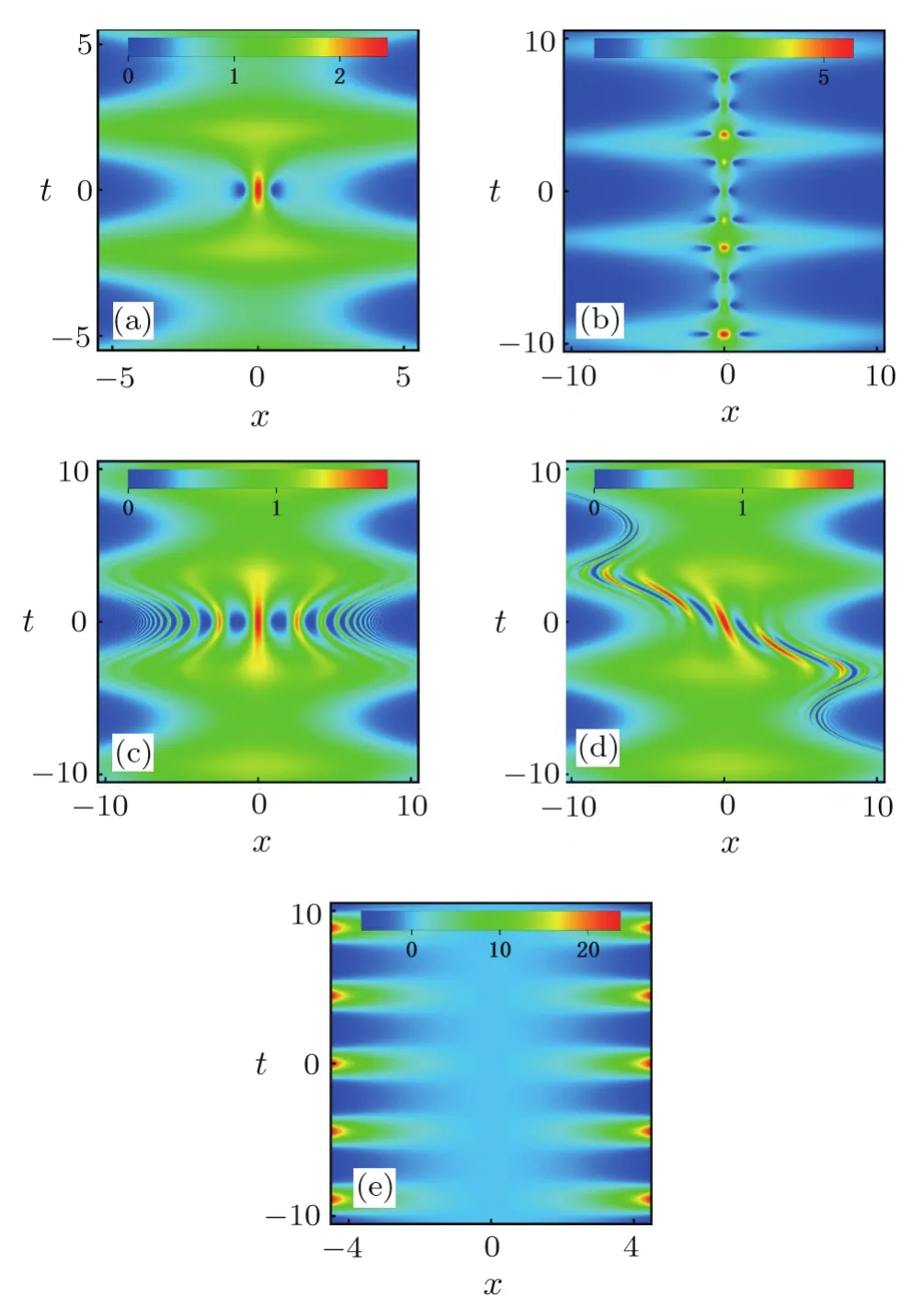
Fig.3 (Color online)Density plot of RW and breathers|ψ|.(a)Rogue wave with µ =1/2,ω0=3/2,b=4,A=1,ω =0.(b)The Kuznetsov–Ma breather withµ =1/2,ω0=1,b=6,A=1,b1=3/2,ω =0.(c)The Akhmediev breather withµ =0.3,ω0=1,b=6,A=1,b1=1/2,ω=0.(d)The general breather solution forµ =0.3,ω0=1,b=6,A=1,b1=1/2,ω =0,a1=1/2.(e)Plot of the potential with b=6,µ=0.5,ω0=1.Other parameter is T0=0.

In the case of Fig.3(e),this potential periodically varies in time and localized in space with attractive and expulsive characteristics.[47]As depicted in Fig.3(a),the rogue wave is localized in both time and space,which is located at(x,t)=(0,0).Figure 3(b)shows that the KM breather has many peaks of varying magnitudes in the evolution direction.In particularly,the contours of each envelope is changed.As show in Figs.3(c)and 3(d),the AB and the general breather are spatially periodic and localized in time.It is clear that the peaks of AB and the general breather have a big stretching in space,which is different with the KM breather.It should be note that the general breather can be seen as an AB with a velocity.Furthermore,whenx→0,the peaks of AB and the general breather increase gradually with the amplitude of background increasing.

4 Nonlinear Waves on Periodic Backgrounds

As we mentioned above,periodic oscillations appear far more common in the nonlinear physical system from a statistical perspective.In this section,we will systematically study the general nonlinear waves on single-and double-periodic backgrounds(i.e.,the optical lattice background).The latter is an important platform for the trapping and manipulation of BECs.[48−49]

4.1 The Single-Periodic Background(g=1)

We consider that the case of the nonlinearity coeffcient is constant.We chooseα=1,F=1 and

witha0∈ (−1,1)andω1∈R.In this case,the dispersion,gain(or loss)term and potential should be elected asf=a/2,γ= −at/2a,andV=0.Ifa0=0,the coeffcients of Eq.(1)are all constants.Equation(1)then reduces to the standard NLS equation,which leads to the standard rogue waves and breathers solutions to Eq.(3).Equation(1)in the above two cases is important both in nonlinear optics and BECs.[36]

In Fig.4,we plot the rogue wave and breathers on single periodic background in the case ofg=1.As can be seen from Fig.4(a),the structure of rogue wave has two valleys placed on both sides of the peak on single periodic background.In Fig.4(b),because of the ratio between the amplitude of the background and the amplitude of nonlinear waves are constant,the KM breather has many peaks of varying magnitudes in the evolution direction.In Fig.4(c),the AB on the single periodic background is similar to the one on the plan wave background.Figure 4(d)illustrates the behavior of the general breather on the single periodic background.In this situation,the structure of the general breather is basically ruined.

4.2 The Single-Periodic Background(g/=1)

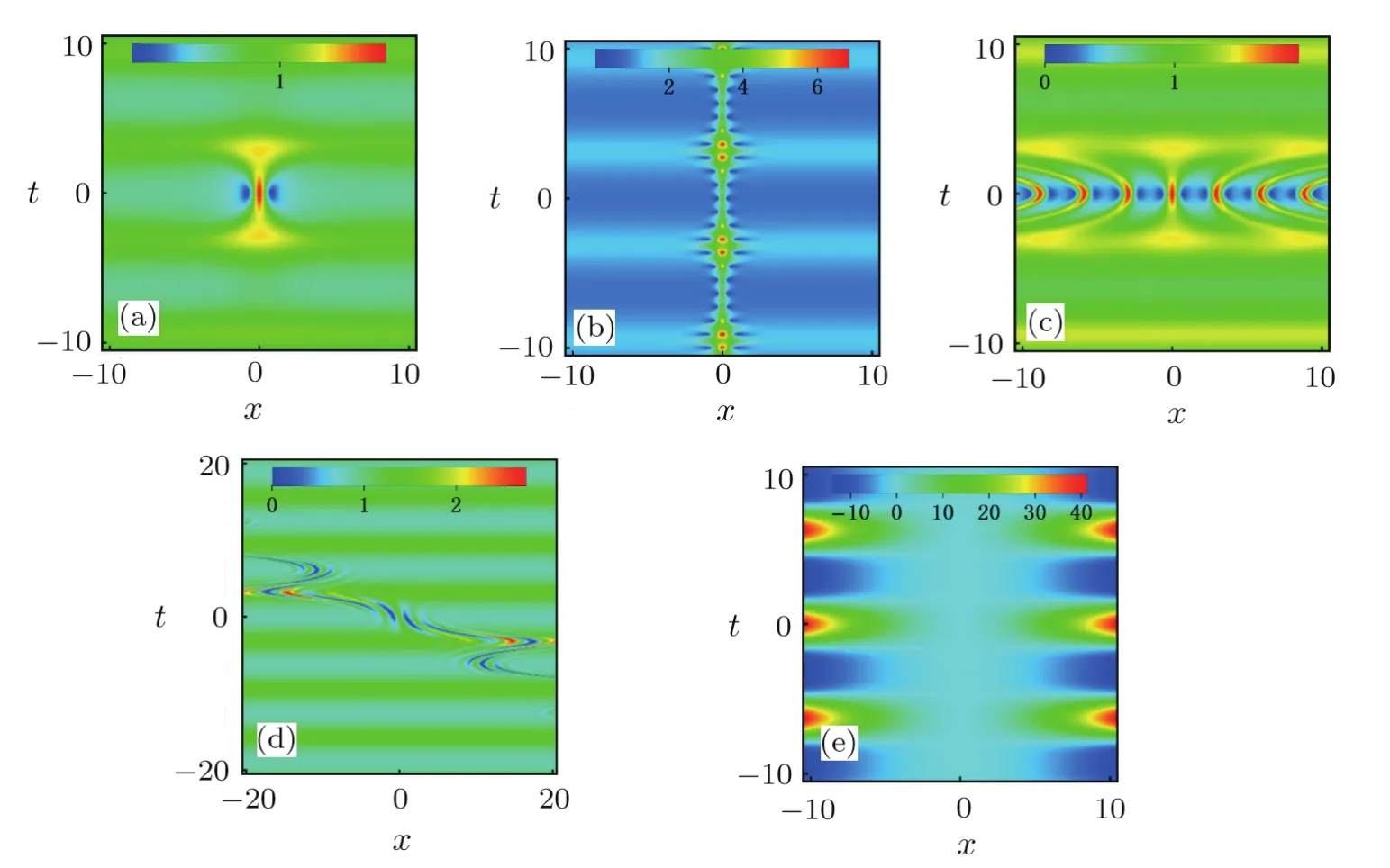
Fig.5 (Color online)Density plot of solutions|ψ|.(a)Rogue wave with A=0.7,ω =0.(b)The Kuznetsov–Ma breather with b1=2,A=1,ω =0.(c)The Akhmediev breather b1=0.7,A=1,ω =0.(d)The general breather with A=1,b1=1/2,Ω=0,µ=1/2.(e)The potential withµ=1/2,ω0=1.Others areµ=1/2,ω0=1,T0=0.

For the singly-periodic background,we choose the nonlinearity coeffcient as

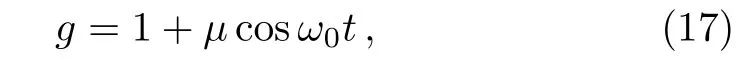
whereFandaas constant,andαis the trigonometric form mentioned in Eq.(13). The dispersion and gain(or loss)term should be chosen asf=1/2α2andγ= −αtx/α.The potential is form of time trigonometric function.

In Fig.5,we plot the dynamics of rogue wave and breathers wave on single periodic background in the case ofg/=1.Figure 5(e)shows that the potential changes from attractive to expulsive behavior periodically.[47]As depicted in Fig.5(a),the structure of rogue wave is different from Fig.4(a).The peak of the rogue wave has a big stretching in evolution direction but the valley has not changed.As show in Fig.3(b),the KM breather is identical to the caseg=1.The AB seem like a periodic rogue wave in distribution direction in Fig.5(c).Figure 5(d)shows that the structure of the general breather is basically ruined.

4.3 The Double-Periodic Background

For the double-periodic background,we choose the nonlinearity coeffcient as

whereF=1/(v+v0cosω2ϖ),α=1 anda(t)to be the function of the trigonometric form as noted in Eq.(16)withv0∈ (−v,v),ω2∈R.vis real constant.With this,we can find the dispersionf=a/2F2and gain(or loss)termγ= −at/2a.The lattice potential is the trigonometric function of time.However,there are few studies on the transportation of rogue wave and breathers in the lattice potential.Base on this research,we will show how rogue wave and breathers propagate on the doubleperiodic background.

In Figs.6(a)–6(d)show the dynamics of the rogue wave and breathers on double periodic background.In Fig.6(a),the single structure of rogue wave is similar to Fig.4(a),but the rogue wave in Fig.6(a)is periodic in distribution direction.Interestingly,the characteristics of KM breather in one period in Fig.6(b)is similar to the KM breather in Fig.4.The KM breather periodically appeared both in the evolution direction and the distribution direction.The peak of AB is not equal in a lattice in Fig.6(c).As shown in Fig.6(d),The general breather can be seen as a tilted AB in a lattice.

Fig.6 (Color online)Evolution of the rogue wave and breathers|ψ|on optical lattice background.(a)Rogue wave with v=3,a0=A=1/2,ω =0,T0= −4.(b)The Kuznetsov–Ma breather with v=3,a0=1/2,A=1,b1=3/2,ω =0,T0= −4.(c)The Akhmediev breather with v=1,a0=b1=1/2,A=1,ω=0,T0=0.(d)The general breather solution T0=−14,v=1,a0=a1=1/2,A=0.8,b1=0.3,ω=0.(e)The potential with v=1,a0=0.8.Others are v0= ω1= ω2=1/2.

5 Conclusions

We have obtained one family of analytical nonlinear localized wave solution for the generalized NLSE with timespace modulation via the method of a combination of the Darboux transformation and similarity transformation.By choosing special forms of the nonlinearityg(x,t),a simple procedure has been established to obtain localized wave solutions on different backgrounds.The solutions exist under certain conditions and impose constraints on the coeffcients depicting dispersion,nonlinearity,gain(or loss),and external potential.We have demonstrated rogue wave and breathers on different localized and periodic backgrounds depending on the corresponding nonlinearity modulations.In particular,the existence and property of localized modes on a double-periodic background under a special designed optical lattice potential were revealed.These results could be of great interest in realizing rogue waves and breathers on different backgrounds in physical systems such as nonlinear optics and Bose–Einstein condensates.

[1]D.J.Kedziora,A.Ankiewicz,and N.Akhmediev,Phys.Rev.E 88(2013)013207.

[2]B.L.Guo,L.Ling,and Q.P.Liu,Phys.Rev.E 85(2012)026607.

[3]L.C.Zhao,G.G,Xin,and Z.Y.Yang,Phys.Rev.E 90(2014)022918.

[4]L.C.Zhao,C.Liu,and Z.Y.Yang,Commun.Nonlinear Sci.20(2015)9.

[5]C.Liu,Z.Y.Yang,L.C.Zhao,et al.,Ann.Phys.362(2015)130.

[6]S.Loomba,R.Gupta,K.K.De,et al.,Opt.Fiber Technol.21(2015)20.

[7]N.Akhmediev,J.M.Soto-Crespob,N.Devinea,and N.P.Hoffmann,Phys.D 294(2015)37.

[8]G.Mu,Z.Qin,et al.,SIAM J.Appl.Math.75(2015)1.

[9]Z.Y.Yan,Commun.Theor.Phys.54(2010)947.

[10]N.N.Akhmediev and V.I.Korneev,Theor.Math.Phys.69(1986)1089.

[11]E.Kuznetsov,A.Akademiia,Nauk SSSR Doklady.236(1977)575;Y.C.Ma,Studies in Applied Mathematics 60(1979)43.

[12]D.H.Peregrine,Appl.Math.25(1983)16.

[13]S.A.Chin,O.A.Ashour,S.N.Nikoli,et al.,Nonlinear Sci.1611(2016)02753.

[14]L.C.Zhao and L.Ling,J.Opt.Soc.Am.B 33(2016)850.

[15]D.R.Solli,C.Ropers,P.Koonath,and B.Jalali,Nature 450(2007)1054.

[16]B.Kibler,J.Fatome,C.Finot,G.Millot,F.Dias,G.Genty,N.Akhmediev,and J.M.Dudley,Nat.Phys.6(2010)790.

[17]J.M.Dudley,G.Genty,and B.J.Eggleton,Opt.Exp.16(2008)3644.

[18]A.Chabchoub,N.P.Hoffmann,and N.Akhmediev,Phys.Rev.Lett.106(2011)204502.

[19]H.Bailung,S.K.Sharma,and Y.Nakamura,Phys.Rev.Lett.107(2011)255005.

[20]J.Fatome,B.Kibler,and C.Finot,Opt.Lett.38(2013)1663.

[21]Y.V.Bludov,V.V.Konotop,and N.Akhmediev,Opt.Lett.34(2009)3015.

[22]G.Yang,L.Li,S.Jia,et al.,Rom.Rep.Phys.65(2013)391;G.Yang,L.Li,S.Jia,et al.,Rom.Rep.Phys.65(2013)902;G.Yang,Y.Wang,Z.Qin,et al.,Phys.Rev.E 90(2014)062909.

[23]Y.Zhang,M.R.Belic,H.Zheng,et al.,Phys.Rev.E 89(2014)03290;Y.Zhang,M.R.Belic,M.S.Petrovic,et al.,Phys.Rev.E 91(2015)032916.

[24]C.G.L.Tiofack,S.Coulibaly,M.Taki,et al.,Phys.Rev.A 92(2015)043837.

[25]C.Liu,Z.Y.Yang,L.C.Zhao,et al.,Opt.Lett.39(2014)1057.

[26]L.Duan,Z.Y.Yang,C.Liu,et al.,Chin.Phys.Lett.33(2016)010501.

[27]A.Chabchoub,N.Hoffmann,M.Onorato,et al.,Phys.Rev.X 2(2012)011015.

[28]D.J.Kedziora,A.Ankiewicz,and N.Akhmediev,Eur.Phys.J.Spec.Top.223(2014)43.

[29]J.L.Shultz,G.J.Salamo,Phys.Rev.Lett.78(1997)855.

[30]V.N.Serkin,A.Hasegawa,and T.L.Belyaeva,Phys.Rev.Lett.98(2007)074102.

[31]J.S.He and Y.S.Li,Stud.Appl.Math.126(2011)1.

[32]J.S.He,M.Ji,and Y.S.Li,Chin.Phys.Lett.24(2007)2157.

[33]Z.Y.Yang,L.C.Zhao,T.Zhang,et al.,Phys.Rev.E 83(2011)066602;J.Opt.Soc.Am.B 28(2011)236;Opt.Commun.283(2010)3768;L.C.Zhao,Z.Y.Yang,et al.,Phys.Lett.A 375(2011)1839;Z.Y.Yang,L.C.Zhao,T.Zhang,et al.,Phys.Rev.A 81(2010)043826;C.Liu,Z.Y.Yang,W.L.Yang,and R.H.Yue,Commun.Theor.Phys.59(2013)311;C.Liu,Z.Y.Yang,M.Zhang,et al.,Commun.Theor.Phys.59(2013)703.

[34]Y.Y.Wang,J.S.He,and Y.S.Li,Commun.Theor.Phys.56(2011)995;S.W.Xu,J.S.He,and L.H.Wang,Europhys.Lett.97(2012)30007;Y.S.Tao,J.S.He,and K.Porsezian,Chin.Phys.B 22(2013)074210.

[35]J.S.He,E.G.Charalampidis,P.G.Kevrekidis,and D.J.Frantzeskakis,Phys.Lett.A 378(2014)577.

[36]K.Manikandan,P.Muruganandam,M.Senthilvelan,and M.Lakshmanan,Phys.Rev.E 90(2014)062905.

[37]J.S.HE,Y.S.Tao,K.Porsezian,and A.S.Focas,J.Nonlinear Math.Phys.20(2013)407.

[38]W.P.Zhong,L.Chen,M.Beli,et al.,Phys.Rev.E 90(2014)043201.

[39]Z.Yan and C.Dai,J.Opt.15(2013)064012.

[40]J.R.He and H.M.Li,Phys.Rev.E 83(2011)066607.

[41]D.Mandelik,H.S.Eisenberg,Y.Silberberg,R.Morandotti,and J.S.Aitchison,Phys.Rev.Lett.90(2003)253902.

[42]C.Liu,Z.Y.Yang,L.C.Zhao,et al.,Phys.Rev.E 94(2016)042221.

[43]C.Q.Dai and W.H.Huang,Appl.Math.Lett.32(2014)35.

[44]L.Wang,M.Li,F.H.Qi,et al.,Eur.Phys.J.D 69(2015)1;L.Wang,X.Li,F.H.Qi,et al.,Ann.Phys.359(2015)97.

[45]C.Liu,Z.Y.Yang,L.C.Zhao,et al.,Phys.Rev.E 91(2015)022904;C.Liu,Z.Y.Yang,L.C.Zhao,et al.,Phys.Rev.A 89(2014)055803.

[46]R.Guo,H.H.Zhao,and Y.Wang,Nonlinear Dyn.83(2016)2475;R.Guo,Y.F.Liu,H.Q.Hao,et al.,Nonlinear Dynamics 80(2015)1221.

[47]W.B.Cardoso,A.T.Avelar,and D.Bazeia,Phys.Lett.A 374(2010)2640.

[48]I.Bloch,Nat.Phys.1(2005)23.

[49]A.D.Cronin,J.Schmiedmayer,and D.E.Pritchard,Rev.Mod.Phys.81(2009)1051.