纵弯模态复合型直线超声电机定子质心振动研究
2018-01-23付前卫姚志远
付前卫, 姚志远
(南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016)
直线超声电机是利用压电单元的逆压电效应激发弹性体的超声振动,通过定子和动子间的摩擦作用,把定子驱动足的微幅振动转化为动子的直线运动[1-4]。由于其具有直接产生直线运动和输出力、定位精度高、结构设计灵活、成本低等优点[5-7],近年来直线超声电机发展十分迅速,在医疗器械[8]、机器人[9]等领域作为驱动器发挥重要作用。通过建立超声电机数学模型,分析电机微幅振动以及动力学特性来优化电机结构,提高超声电机的机械输出特性是研究的重点,而速度稳定性等机械特征与定子的质心振动有关,本文重点对此进行理论建模分析和实验验证。
超声电机的输出特性与电机定子的振动模态、接触界面的摩擦特性、预压力大小等有关,很难建立一个普适的模型。因此通常引入特定假设,建立一个针对研究对象的适用模型[10]。其中建模的难点之一在于驱动足和摩擦界面之间的接触模型的建立。文献[11]没有考虑定、转子接触界面径向摩擦和黏滞现象,使得模型无法对大力矩超声电机进行合理分析。文献[12]较为完整地分析了陶瓷片逆压电效应激振以及定、转子摩擦传动过程,但模型过于复杂,缺乏实用性。陈超等[13]通过阐释行波型旋转电机三维接触驱动机理,建立整机动力学模型,证明了定、转子在界面径向滑移所导致的能量损耗对电机输出性能的影响。王金鹏等[14]通过行波型旋转电机结构改进,改善了电机接触界面周向压力不均现象,降低了空载速度波动率。罗辞勇等[15]利用李雅普诺夫稳定性判据对行波型旋转电机驱动区间和制动区间进行了分析并讨论了其对电机输出速度、转矩等的影响。现有文献主要关注旋转电机接触问题,缺乏对于直线超声电机相关模型研究的报道。许海等[16]假设直线超声电机定、动子接触为弹性体接触,并将接触层等效为线性弹簧层,分析了摩擦等对电机输出特性的影响。而目前研究表明,定子驱动足振幅和接触层变形量并不相等,接触层起非线性弹簧作用[17]。以非线性弹簧接触模型为基础,对直线超声电机进行动力学建模、输出稳定性的研究相对较少。文献[18]进一步研究了驱动足质点的椭圆运动对电机动子运动的影响规律以及定子质心振动对驱动足椭圆轨迹的影响,解释了电机的输出特性与预压力、摩擦材料刚度等之间的关系。但是文章较多的分析的是定子质心振动对电机输出特性的影响,而缺少质心振动规律的深入研究,且在对定子质心振动分析时,仍将摩擦材料层等效为线性弹簧层,这与实际接触情况稍有差别。Li等[19]对直线超声电机定、动子碰撞振动模型进行黏滞运动分析时,也对定子质心运动进行相应讨论,但缺乏实验验证。
本文以典型的纵弯模态复合直线超声电机为研究对象[20-21],假设定、动子间的定子表面存在弹性层,该弹性层简化为刚度较大的非线性弹簧层。将纵、弯模态解耦,以一阶纵振为例,建立定子法向运动的动力学模型,根据定子质心振动方程解出质心振动稳态解,通过仿真分析得出不同预压力弹簧刚度、不同预压力等对质心振动响应的影响以及质心振动对电机性能的影响。最后通过实验验证了本文模型的有效性。
1 定、动子接触模型
本文主要分析定、动子间的接触,研究定子质心振动的规律,因此,建立电机在接触面法向的动力学模型。图1所示的是纵弯复合模态型直线超声电机的定子,在一阶纵振模态下的驱动足法向运动结构原理图。该结构为夹心式超声电机,其中压电陶瓷片安装在定子中心,夹持位于振动的节点上。
对于旋转超声电机而言,由于摩擦材料材质较软,相关研究的普遍做法是将摩擦材料等效成分布式线弹簧。但直线电机常用的摩擦材料的刚度和硬度都比金属材质的驱动足大,其粗糙度比驱动足小很多,实际接触时动足的变形量比摩擦界面的变形量大,且驱动足的变形主要来自于其表面的变形。因此对于直线超声电机,等效线性弹簧的接触模型不成立,本文将摩擦材料的摩擦界面看成是一个光滑的刚性面,将驱动足与它的接触等效成一个带有弹性层(用分布的非线性弹簧表示)的刚性柱体与一个刚性平面的接触模型,如图2所示。
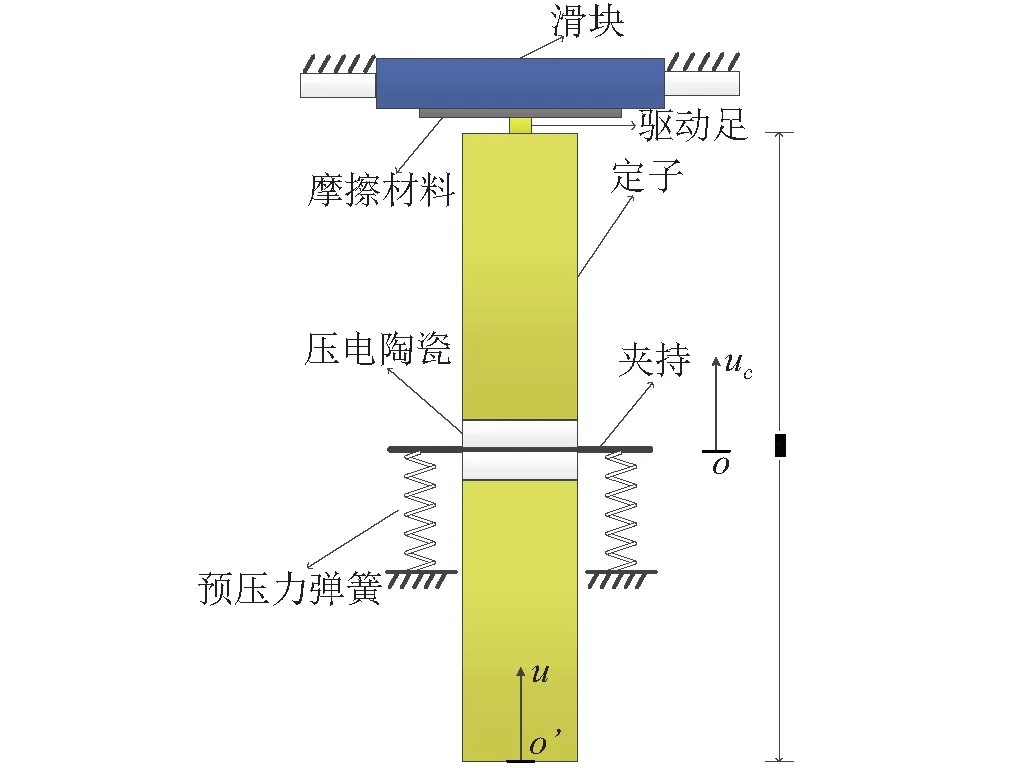
图1 电机定、动子法向接触物理模型Fig.1 Stator and rotor normal contact physical model
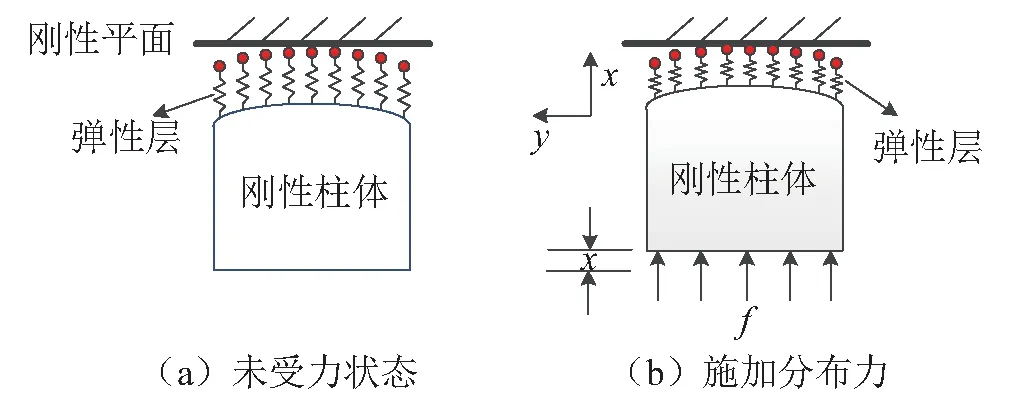
图2 电机定、动子等效接触模型Fig.2 Equivalent contact model of motor stator and rotor
图2(a)表示的是驱动足未受力时的情形,图2(b)表示的是驱动足在下端受到一个分布力f的作用,弹性层在x方向上产生的变形量记为x,它们之间的关系由一个三次多项式函数[22]表示
f(x)=a3x3+a2x2+a1x
(1)
式中:a1=42.3;a2=-0.123;a3=44.2。
2 定子动力学建模
本文进一步将接触模型中的弹性层部分简化为一个非线性弹簧,如图3所示为整个定子的法向振动过程。
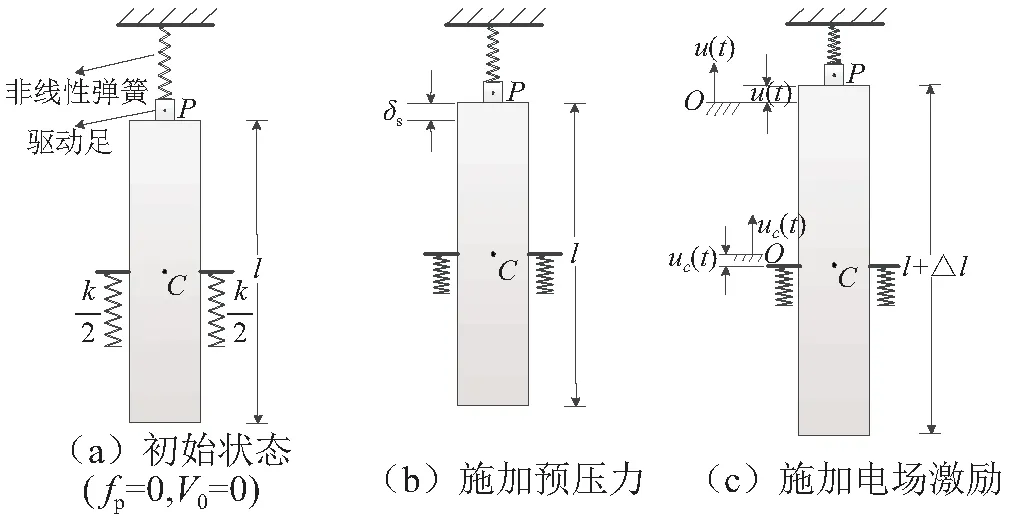
图3 定子法向运动模型Fig.3 Normal motion model of stator
图3(a)表示未施加预压力和电场时的定子的情况,图3(b)表示通过给预压弹簧一个压缩量为定子施加一个预压力,此时驱动足的位移为δs,整个定子受力平衡。图3(c)表示在图3(b)的基础上再给定子施加一个激励电场,激发出定子的纵振模态(定子的变形量为Δl)。由于定子顶端的等效非线性弹簧的刚度要比预压弹簧的刚度大得多,致使定子在伸缩的过程中,定子的质心也产生振动,即定子的法向运动由定子纵振运动和质心的运动叠加而成。则点P(驱动足表面以下部分的质心)的位移可由定子在l处的纵振位移和质心的位移叠加而成
u(t)=u1(l,t)+uc(t)
(2)
式中:u1(l,t)为定子在处的一阶纵振的位移,参考系为定子本身,坐标原点为O′, 时间t=0时,驱动足质点P的一阶纵振位移ul(l,0)定义为点P的位置0点;uc(t)为质心C的位移,参考系为地面,时间t=0时,为位移0点,质心位于坐标原点O处;u(t)为点P的位移。摩擦界面受到的法向压力可由以下分段函数表示
(3)
式中, 当u(t)+δs>0时,驱动足与摩擦界面接触,而当u(t)+δs≤0时,驱动足与摩擦界面脱离,显然,此时摩擦界面所受的法向压力变为0。
为了研究定子质心的振动,将其简化为一个单自由度系统,振动过程分析如图4表示。
图4(a)表示未施加预压力和电场时的定子的情况,图4(b)表示通过给预压弹簧一个压缩量δc为定子施加一个预压力fp(即kδc=fp),此时,质量块受力平衡。图4(c)表示给定子施加一个电场后,质量块上端受到来自于摩擦界面产生的时变法向压力,造成质量块受力不平衡,从而使质量块产生运动,记质量块的位移为uc(t)。
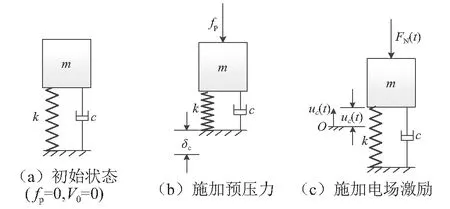
图4 定子质心振动简化模型Fig.4 Vibration model of center of stator mass
下面分别建立定子一阶纵振模态和定子质心振动的动力学方程。首先,由图3可知定子的一阶纵振运动可以等效成一个两端自由杆在x=l处受到集中力FN(t)作用后的受迫振动,利用能量原理和杜哈梅积分(将集中力化成分布力)可得到定子一阶纵振模态的动力学方程
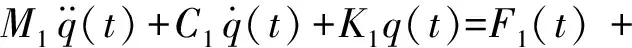
(4)
式中,M1,K1,C1,F1(T),φ1(l)分别为定子在两端自由状态下的一阶纵振的模态质量、模态刚度、模态阻尼、模态力和x=l处的振型。由图4不难得到定子质心振动的动力学方程
(5)
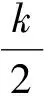
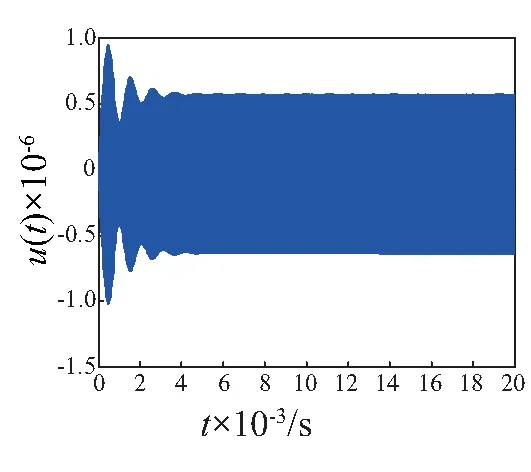
图5 不考虑质心振动的点P位移Fig.5 Displacement of P without considering the center of mass vibration

图6 考虑质心振动的点P位移Fig.6 Displacement of P considering the center of mass vibration
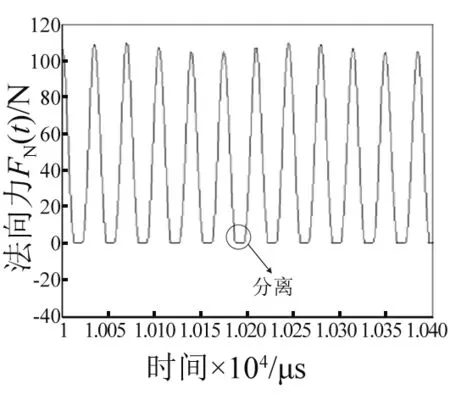
图7 摩擦界面所受的法向压力Fig.7 Normal pressure of friction interface
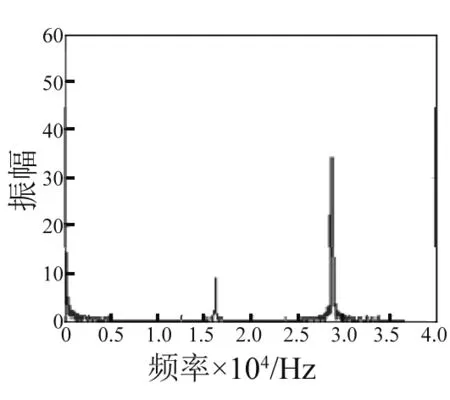
图8 法向压力的频域分析(FFT)Fig.8 FFT analysis of normal pressure
图5和6所示的分别是不考虑质心振动时质点P的位移响应和考虑质心振动时的位移响应,稳态情况下两种位移振幅基本相当,但稳态时的平衡位置却有较大差异,不考虑质心振动时,点P的稳态的平衡位置位于坐标的原点处,当考虑质心振动时其平衡位置就偏离了坐标原点。这说明质心振动的稳态振幅相对于定子一阶纵振模态的稳态振幅小。造成其平衡位置就偏离了坐标原点则假设质心振动可能存在一个静位移。图7所示为点P稳态振动下,摩擦界面受到的法向压力,从图中可知法向压力基本上是一个随时间变化周期函数。图8所示的是利用FFT对稳态振动下法向压力信号进行频域分析。由图8可知这个信号中主要包含两个频率成分,一个是超声频率(大约28 kHz),这个频率主要和定子的一阶纵振模态有关,而另一个相对低一些的频率成分(大约16 kHz)和质心的振动有关。
3 定子质心振动稳态解
由于FN(t)可以近似看成是周期函数, 令FN(t+T0)=FN(t), 将FN(t)展开成Fourier级数
(6)
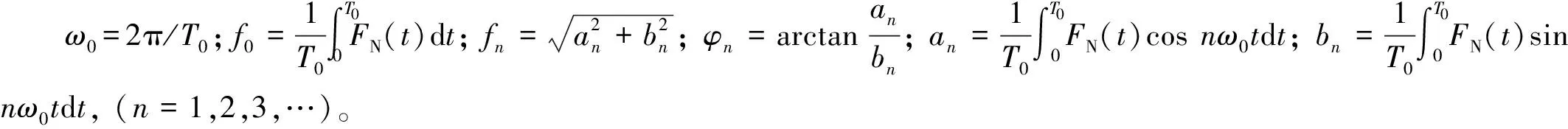
将式(6)代入式(5)得
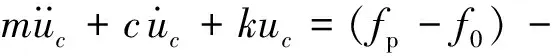
(7)
则不难得到质心的稳态解
(8)
其中,
(9)
(10)
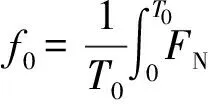

图9 不同预压弹簧刚度下质心的位移响应Fig.9 Displacement response of the center of mass under different spring stiffness
图10所示的是不同预压力下定子质心的位移响应,图11是对应的质点P的稳态响应,从这两幅图中可以看出当预压力比较小时,定子质心稳态振动的平衡位置向下偏离其坐标原点的距离比较大,从而造成质点P的稳态振动的平衡位置向下偏离其坐标原点的距离比较大,因此会造成驱动足与滑块的脱离时间比较长,不利于电机的动力输出。而增大预压力后,会使质心稳态振动的平衡位置向下偏离其坐标原点的距离变小。图12所示的是不同预压力摩擦界面所受的法向压力的情况,从图中可以看出,当预压力比较小时(fp=10 N),驱动足在一个周期内的很大一部分时间内都是与滑块脱离的,可能会造成驱动足的有效驱动力较小。而当预压力比较大时(fp=40 N),驱动足在一个周期内的很大一部分时间内都与滑块接触,造成驱动足对动子(滑块)的制动作用时间增长,不利于电机的动力输出,而且当预压力继续增大时(fp=60 N),驱动足将不与滑块脱离,这会大大降低电机的动力输出,甚至造成不能驱动的情况。
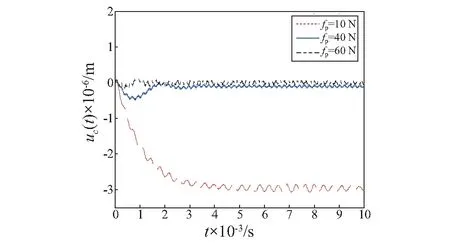
图10 不同预压力下质心的位移响应Fig.10 Displacement response of center of mass under different pre-pressure

图11 不同预压力下质点P的稳态响应Fig.11 Displacement response of P under different pre-pressure
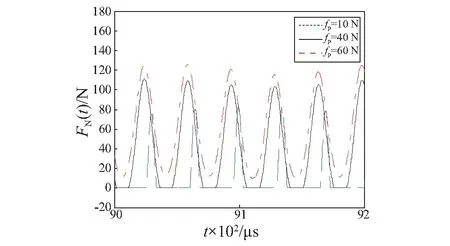
图12 不同预压力下摩擦界面所受的法向压力Fig.12 Normal pressure of friction interface under different pre-pressure
4 实验验证
为验证模型的有效性,利用KEYENCE LK-H150型号高速激光位移传感器对样机进行振动测试,采样频率为100 kHz。如图13所示为实验装置。定子质心是一个物理概念,无法测量,因此实验将传感器激光点照射在定子中部的夹持中点(和定子质心在同一铅垂面),该点的位移响应能够反映出质心振动情况,如图14所示。

图13 位移响应测试Fig.13 Displacement response test
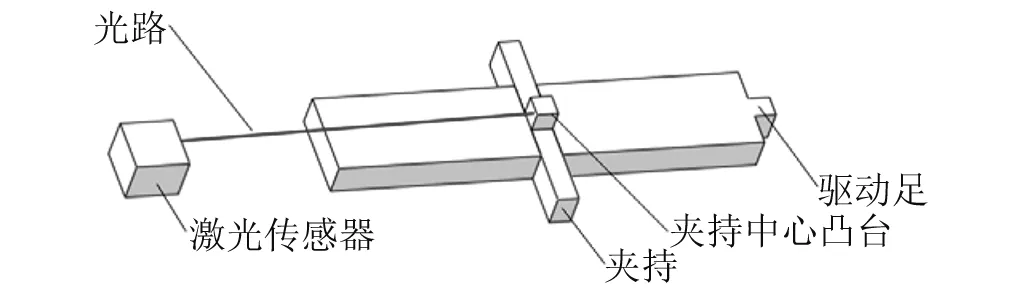
图14 定子质心位移响应测试示意图Fig.14 Displacement testing schematic of center of stator mass
选用刚度分别为63 750 N/m和9 750 N/m的SWOSC-V材质矩形截面模具弹簧来施加预压力,在预压力大小为30 N时,测试点稳态响应如图15所示。由图可知,两种情况下稳态响应的平衡位置偏离坐标原点;两条曲线采样点的位移稳态响应平均值的差值仅为0.25 μm,预压力弹簧刚度对于静位移B0影响不大。与理论分析结果以及图9所示位移稳态响应曲线走势较为吻合。

图15 不同弹簧刚度下质点稳态响应Fig.15 Center of mass displacement response under different spring stiffness
选用刚度为9 750 N/m的同种弹簧,根据形变量调节预压力大小分别为10 N,40 N,60 N进行实验。测试点稳态响应如图16所示。表1为不同预压力下位移稳态响应平均值对比,其中理论值选取图10曲线0.005~0.01 s稳态响应区间对应的平均值。
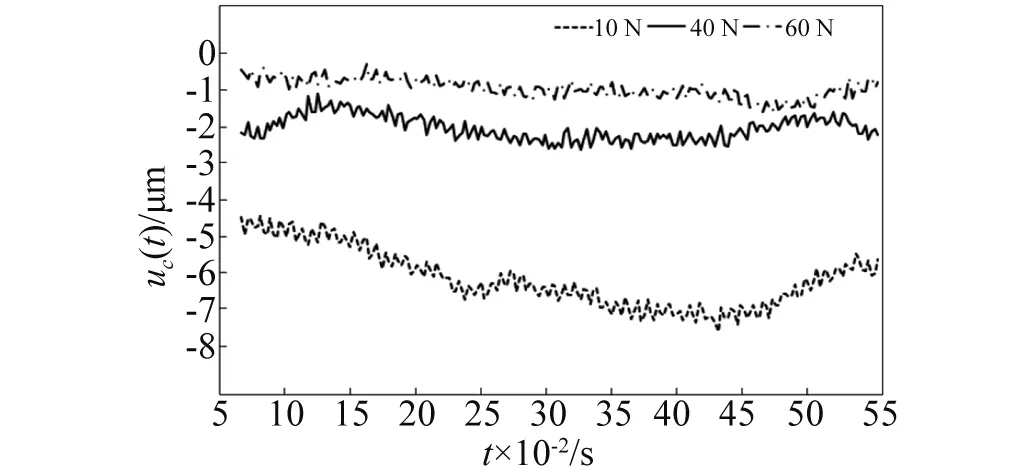
图16 不同预压力下质点稳态响应Fig.16 Center of mass displacement response under different pre-pressure
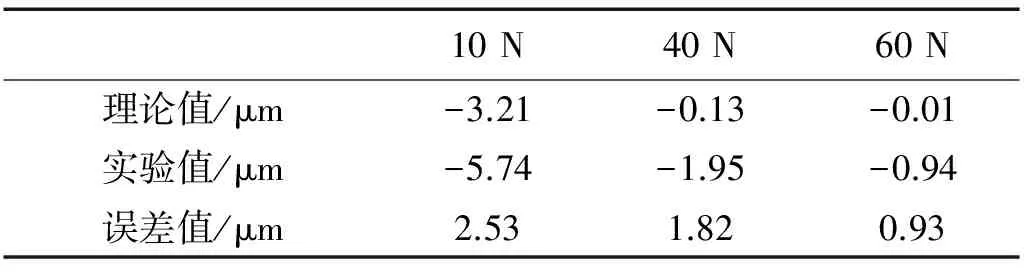
表1 位移稳态响应平均值
由表1可知,理论值与实验值均表明不同预压力对于质心位移稳态响应具有明显影响。其中,在预压力较小的情况下,测试点稳态响应偏离坐标原点较大,将对电机的输出特性具有不利影响,与仿真结果吻合。
5 结 论
本文根据建立的定、动子刚性平面接触模型和定子法向运动的动力学模型,得出定子质心振动的动力学方程稳态解,发现质心稳态位移中的静位移使得质心的稳态平衡位置偏离其坐标原点,并分析了其对驱动足的法向运动的影响。模型表明预压弹簧的刚度对定子质心稳态平衡位置的偏离影响不大,而预压力对质心振动和驱动足法向运动具有明显影响,进而影响电机的输出特性。预压力太小,造成定子质心稳态平衡位置偏离原点过大,驱动足对滑块的有效驱动时间太短;预压力过大时,会造成驱动足与滑块始终接触不脱离。文章通过测试不同预压力弹簧刚度和不同预压力对定子质心的偏移验证了动力学模型是有效的,该研究可以为直线超声电机的动力学建模和结构优化设计提供依据。
[ 1 ] 赵淳生. 超声电机技术与应用[M]. 北京:科学出版社,2007: 313-317.
[ 2 ] 张健滔, 李朝东, 何晓菁. 卧板式直线超声电机的特性分析模型[J]. 中国电机工程学报, 2012(18):137-144.
ZHANG Jiantao, LI Chaodong, HE Xiaojing. Modeling for characteristic analysis of a plate-type linear ultrasonic motor[J]. Proceedings of the CSEE, 2012(18): 137-144.
[ 3 ] 丁庆军, 姚志远, 郑伟,等. 行波型超声电机定子摩擦材料的研制及其摩擦磨损性能研究[J]. 摩擦学学报, 2007, 27(6): 578-582.
DING Qingjun, YAO Zhiyuan, ZHENG Wei, et al. Experimental study of friction material adhere to the stator of the traveling wave type rotary ultrasonic motor[J]. Tribology, 2007, 27(6): 578-582.
[ 4 ] 曲焱炎, 曲建俊, 袭建军. 驻波超声电机摩擦材料ABAQUS特性仿真计算与研究[J]. 电机与控制学报, 2014, 18(12): 95-101.
QU Yanyan, QU Jianjun, XI Jianjun. ABAQUS simulation and research of frictional material for standing wave ultrasonic motor[J]. Electric Machines and Control, 2014, 18(12): 95-101.
[ 5 ] 贺红林, 何文丛, 刘文光. U型变截面薄板面内复合模态驱动的直线超声电机[J]. 振动与冲击, 2014, 33(18): 65-71.
HE Honglin, HE Wencong, LIU Wenguang. A linear ultrasonic motor driven by an U-shaped stator’s in-plane hybrid vibration modes[J]. Journal of Vibration and Shock, 2014, 33(18): 65-71.
[ 6 ] 王金鹏,周宏平,时运来. 直线超声电机驱动的精密运动平台的位移分辨率[J]. 振动与冲击, 2015, 34(22): 178-182.
WANG Jinpeng, ZHOU Hongping, SHI Yunlai. Displacement resolution of precision stage driven by linear ultrasonic motors[J]. Journal of Vibration and Shock, 2015, 34(22): 178-182.
[ 7 ] 李向华, 陈超, 赵淳生. 非接触式直线型超声电机的振动分析[J]. 振动与冲击, 2010, 29(7):149-152.
LI Xianghua, CHEN Chao, ZHAO Chunsheng. Vibration studies of non-contact linear ultrasonic motor[J]. Journal of Vibration and Shock, 2010, 29(7): 149-152.
[ 8 ] MASHIMO T, TOYAMA S. Micro rotary-linear ultrasonic motor for endovascular diagnosis and surgery[C]//IEEE International Conference on Robotics and Automation. Pasadena: IEEE, 2008: 3600-3605.
[ 9 ] 王赟, 姚志远, 耿冉冉. 直线超声电机驱动的并联微操作手的结构设计[J]. 机器人, 2015, 37(5):573-580.
WANG Yun, YAO Zhiyuan, GENG Ranran. Structure design of a parallel micromanipulator driven by ultrasonic motors[J]. Robot, 2015, 37(5): 573-580.
[10] 颜佳佳, 阮新波. 旋转型行波超声电机的等效电路模型[J]. 中国电机工程学报, 2009, 29(15): 80-87.
YAN Jiajia, RUAN Xinbo. Electrical equivalent circuit model of traveling wave type rotary ultrasonic motor[J]. Proceedings of the CSEE, 2009, 29(15): 80-87.
[11] MOAL P L, MINOTTI P. A 2D analytical approach of the stator-rotor contact problem including rotor bending effects for high torque piezomotor design[J]. European Journal of Mechanics-A/Solids, 1997, 16(6): 1067-1103.
[12] 陈超. 旋转型行波超声电机理论模型的研究[D]. 南京:南京航空航天大学, 2005.
[13] 陈超, 赵淳生. 旋转型行波超声电机中三维接触机理的研究[J]. 中国电机工程学报, 2006, 26(21): 149-155.
CHEN Chao, ZHAO Chunsheng. Study on the three dimensional contact mechanism of traveling wave type rotary ultrasonic motor[J]. Proceedings of the CSEE, 2006, 26(21): 149-155.
[14] 王金鹏, 金家楣, 赵淳生. 行波型旋转超声电机速度稳定性研究[J]. 中国电机工程学报, 2011, 31(30): 109-116.
WANG Jinpeng, JIN Jiamei, ZHAO Chunsheng. Velocity stability research of traveling wave type rotary ultrasonic motor[J]. Proceedings of the CSEE, 2011, 31(30): 109-116.
[15] 罗辞勇, 张帆, 杜劲超. 行波型超声电机的稳定性分析[J]. 重庆大学学报, 2014, 37(2): 46-53.
LUO Ciyong, ZHANG Fan, DU Jinchao. Stability study of the traveling wave ultrasonic motor[J]. Journal of Chongqing University, 2014, 37(2): 46-53.
[16] 许海, 赵淳生. 直线型驻波超声电机的定、动子间接触及摩擦分析[J]. 南京航空航天大学学报, 2005, 37(2): 144-149.
XU Hai, ZHAO Chunsheng. Contact process and friction analysis of linear ultrasonic motor[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2005, 37(2): 144-149.
[17] 周胜利, 姚志远. 直线超声电机定/动子接触的微观力学模型[J]. 振动与冲击, 2012, 31(20): 90-93.
ZHOU Shengli, YAO Zhiyuan. Micromechanic model for contact between a linear ultrasonic motor’s stator and mover[J]. Journal of Vibration and Shock, 2012, 31(20): 90-93.
[18] 万志坚, 胡泓. 面内弯纵型直线超声电机的驱动与摩擦分析[J]. 振动、测试与诊断, 2014, 34(2): 229-236.
WAN Zhijian, HU Hong. Analysis on friction driving of linear ultrasonic motor with in-plane bending and longitudinal mode[J]. Journal of Vibration, Measurement and Diagnosis, 2014, 34(2): 229-236.
[19] LI X, YAO Z, WU R. Modeling and sticking motion analysis of a vibro-impact system in linear ultrasonic motors[J]. International Journal of Mechanical Sciences, 2015, 100: 23-31.
[20] TSAI M S, LEE C H, HWANG S H. Dynamic modeling and analysis of a bimodal ultrasonic motor [J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 2003, 50(3): 245-256.
[21] WAN Z, HU H. Modeling and experimental analysis of the linear ultrasonic motor with in-plane bending and longitudinal mode[J]. Ultrasonics, 2013, 54(3): 921-928.
[22] ZHOU S, YAO Z. Design and optimization of a modal-independent linear ultrasonic motor[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2014, 61(3): 535-546.
