基于动力反共振结构的周期细直梁纵向局域共振带隙研究

刘扭扭， 张振果， 徐时吟， 华宏星

(1. 上海交通大学 机械系统与振动国家重点实验室，上海 200240; 2. 上海交通大学 振动、冲击及噪声研究所，上海 200240)

梁类结构是各类机械系统的基本构件，是振动与噪声传递的重要载体，其振动隔离问题一直是广大学者关注的焦点。Kushwaha等[1]，通过类比光子晶体，首次提出利用具有弹性波带隙的周期性复合材料或结构(声子晶体)来抑制带隙范围内弹性波的传播。

声子晶体带隙形成机理包括布拉格散射型和局域共振型两大类型[2-3]。传统的声子晶体带隙产生机理为Bragg散射机理，带隙产生的原因是周期变化的材料特性与弹性波之间的耦合作用[4]，第一带隙的中心频率约为c/2a， 其中c为弹性波在基体材料中的波速，a为周期结构的晶格常数。在材料结构已知的条件下若想获得低频带隙必须要选取大的晶格常数，一般不可能在晶格常数为几厘米或更小的情况下得到1 kHz以下的低频带隙，因此在实际使用中受到诸多限制。

Liu等[5]首次提出了局域共振带隙机理，突破了传统布拉格带隙机理的限制，可以在较小的晶格常数条件下获得较低的低频带隙。郁殿龙[6]通过理论和实验研究验证了局域共振带隙的存在，并构造出了具有低频禁带的一维纵向小尺寸声子晶体结构；在此基础上肖勇[7]对弹性波的纵向隔振机理进行了较全面的分析。

Flannelly[8]利用惯性耦合能够产生反共振频率的特点，提出了一种动力反共振的隔振结构，Rita等[9-11]将其用于航空航天工业领域。Ivovich等[12]把这种隔振器用来隔离从机器传递到基础的低频振动，Platus[13]采用相同的原理设计了液压杠杆系统，可以克服机械杠杆不能实现的大杠杆比结构。Yilmaz等[14]系统的分析了动力反共振的动力学特性。其原理示意图如图1所示，由于杠杆可以放大ma的惯性力，相当于增加系统的等效质量，因此采用相同的参数它会产生更小的共振频率。

本文拟结合周期结构局域共振带隙机理和动力反共振结构的惯性耦合机制，构造出一种具有低频局域共振带隙的周期结构。

首先介绍基于动力反共振周期结构的局域共振带隙计算的理论，并通过有限元进行验证；进而讨论参数对局域共振带隙的影响因素及其规律，最后从等效质量和等效刚度的角度阐明动力反共振结构作为局域共振子的优势。

1 细直梁的局域共振带隙计算

1.1 基于传递矩阵法的带隙计算

如图1所示为新型共振子结构，将其沿均质杆纵向周期布置，如图2所示。其中每个振子的刚度为k，杠杆上的悬挂质量为ma，主质量为m，晶格常数为a。作如下假设：

(1) 共振子与梁连接的部分为刚性点连接且无质量；

(2) 杠杆为刚性无质量杆，仅考虑悬挂惯形体的质量；

(3) 各个铰链的阻尼和摩擦均不计；

(4) 弹簧为无质量、线性且无阻尼的弹簧；

(5) 主质量为刚性块；

(6) 不考虑基座的质量；

(7) 振动为小振动。

令细直梁未变形时的轴线为u轴，垂直于轴线的坐标为v轴。

梁纵向振动的运动方程为

(1)

式中：u(x,t)为纵向位移；E为弹性模量；A为横截面积。

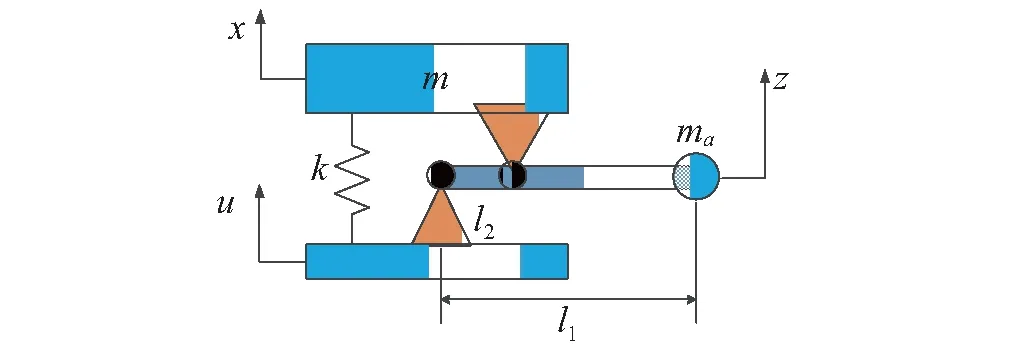
图1 单个共振子示意图Fig.1 Schematic diagram of a single resonator

图2 无限长细直梁局域共振周期结构Fig.2 An infinite beam with a periodic array of local resonant resonators

共振子结构将杆分为n段， 取其中第n段梁为例，式(1)的解可写为

(2)

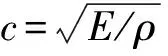
第n个共振子振动方程为

x=Xe-iωt

(3)

式中，X为第n个振子的振幅。

在第n段和第n-1段细直梁的连接处满足位移连续、力平衡条件

(4)

式中，F为共振子传递到杆上的力。

对共振子进行动力学分析， 第n个振子动能和势能可分别表示为

(5)

(6)

其中，z,x,u满足如下关系

z=(1-α)u+αx

(7)

以及α=l1/l2为杠杆比。

联立式(5)～式(7)，利用拉格朗日方程可以得到

(8)

联立式(2)、式(3)和式(8)可得

(9)

则该共振子传递到杆上的力F为

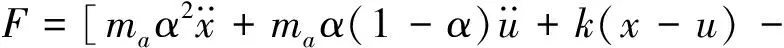
(10)

将式(10)代入式(4)中第二式可得到

(11)

其中，

(12)

把力F的表达式(10)代入式(4)并写成矩阵的形式

Kψn=Hψn-1

(13)

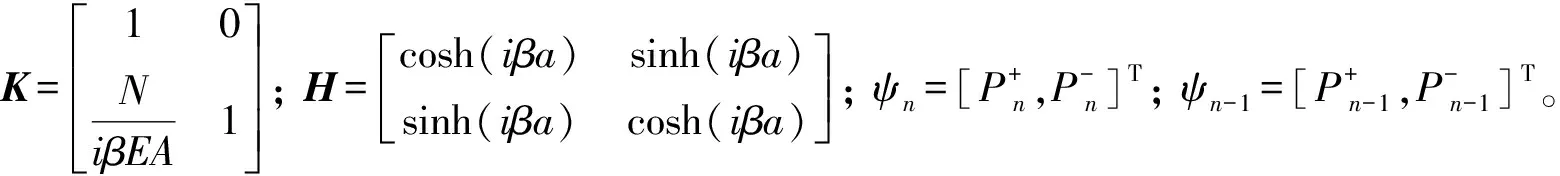
梁在x方向上是无限周期结构， 矢量ψn满足Bloch定理[15]

ψn=eiqaψn-1

(14)

式中，q为波矢(一维时也称为波数，为标量)。

由式(13)和式(14)可得

|T-eiqaI|=0

(15)

式中：T=K-1H；I为4×4的单位矩阵。

根据式(15)可以得到系统的波矢(±q1或±q2)和ω之间的关系即系统的能带结构，q的符号代表本征波的传播方向不同。由于周期性，本文将Re(q)的范围限定在[-π/a,π/a]区间内。显然Re(q)描述的是本征波传播通过单位长度的相位变化，Im(q)描述的是本征波传播通过单位长度的幅值衰减，则当Im(q)为不同值时所对应的波的衰减程度也将不同，因此可以将本征波的传播在一个频带范围内划分为几个不同的区域：

(a) 当0≤Re(q)≤π/a且|Im(qa)|≠0时所对应的本征波为衰减波，同时经过一个周期后本征波的相位变化介于0和π之间，满足这个条件的频带范围即为本征波的阻带即带隙；

(b) 当0≤Re(q)≤π/a且|Im(qa)|=0时所对应的本征波无衰减，同时经过一个周期后的本征波的相位变化介于0和π之间，满足这个条件的频带范围为本征波的通带。

2 数值计算与有限元计算

文献[4]中提出了一种以弹簧质量为共振子、以有机玻璃为基体材料的一维声子晶体，并证实了在这种结构下局域共振带隙的存在性。本文为实现更低的带隙起始频率，提出了一种以动力反共振为共振子的一维声子晶体结构。为了与文献[4]进行对比，所采用的结构参数及材料常数均与文献[4]中保持一致。

梁的长度取为0.8 m，弹性模量E=4×109Pa，密度为ρ=1 000 kg/m3，b=10 mm和h=5 mm；振子主质量为30 g，悬挂质量为20 g，弹簧刚度为k=106N/m，杠杆比取α=2。

利用式(15)可以计算得到无限周期结构细直梁在0～1 500 Hz内的能带图如图3所示。利用节1中判断带隙的方法，由图3可以判断出在这种结构下系统的带隙，为：473～1 234 Hz。文献[4]在相同的参数条件下的带隙为690～3 228 Hz。显然，本文所提出的共振子周期结构，带隙的起始频率比文献[4]中的低了超过200 Hz,带宽要小于文献中的带宽，但实际工程中，比如潜艇轴系的纵向隔振中，往往需要隔离的是低频振动而且往往带隙并不需要这么宽。

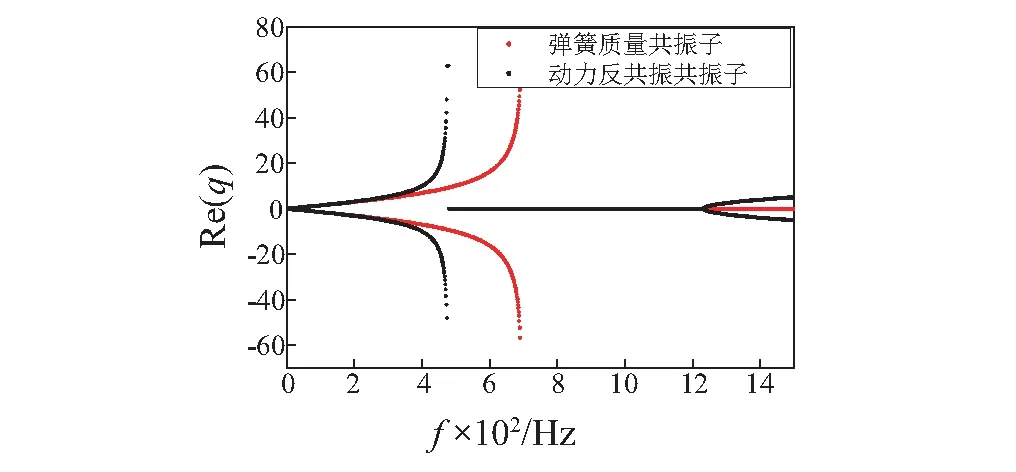
(a) 实部

(b) 虚部图3 无限周期结构的细直梁能带结构的波矢实部和虚部Fig.3 Complex band structure of longitudinal wave vector real part and imaginary part

作为验证，本文利用有限元软件ANSYS建立了该结构的有限元模型以分析计算在有限周期结构条件下，弹性波的传播特性。图4所示为10个周期的细直梁的有限元模型图。在梁的左端施加纵向单位位移，使得梁的纵向弹性波沿X轴传播，在10个、20个、30个、40个振子的条件下通过计算右端响应得到弹性波的传播带隙，结果如图5所示。

图4 细直梁的局域共振周期结构有限元模型Fig.4 Finite element model of uniform beam with ten unit cells

由图5可以看出在上述两种情况下，细直梁带隙出现的位置基本一样，均为：469～1 225 Hz，与无限周期结构的解析结果吻合较好，证明了解析解的正确性。计算结果表明：随着振子数量增加，弹性波在带隙范围内的衰减也逐渐增加，证明了在细直梁上周期性安装这种共振子可以使弹性波产生带隙。值得关注的是，弹性波只在带隙起始频率处有明显的衰减，之后随着频率的增加，弹性波衰减幅度明显减小，这也正是局域共振带隙的特点。

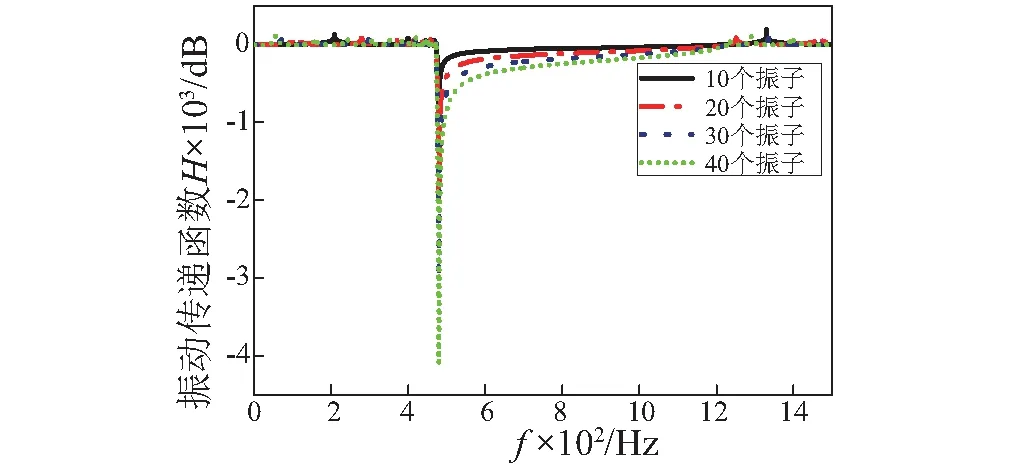
图5 细直梁局域共振的位移传递函数Fig.5 Transfer function of local resonant beam

3 参数分析

如图1所示，动力反共振结构要比文献[4]中所提的弹簧质量共振子结构更为复杂，拥有更多的参数。第二节的算例给出了在特定参数条件下动力反共振结构的能带结构，在此基础上，本节将进一步研究动力反共振结构的参数变化对一维声子晶体的能带结构的影响。

动力反共振结构包括：刚度k，主质量m，悬挂质量ma及杠杆比α。由于k已定，本节将通过两个算例分别对杠杆比α以及主质量m和悬挂质量ma的分配进行分析。

算例一中，保持质量分配不变，考察杠杆比α对带隙的影响规律。根据定义α≥1，这里分别取α为2，3，4，5；利用式(15)可以计算出在这几种情况下的能带结构，由于通过波矢的虚部就可以完全表示出带隙的位置、宽度以及衰减的幅值，因此在此仅列出式(15)中波矢的虚部解，结果如图6所示。

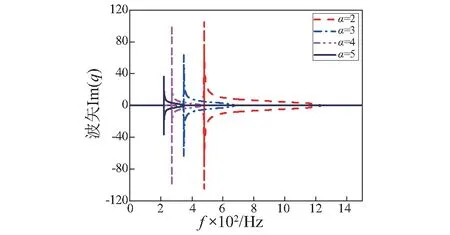
图6 不同杠杆比下细直梁局域共振的波矢Fig.6 Wave vector of local resonant beam with different lever ratio

由图6可以看出：当α取2，3，4，5时系统的带隙所在的频率范围分别为：473～1 233 Hz；344～675 Hz；268～462 Hz；218～349 Hz。随着杠杆比的增加带隙的起始频率逐渐减小，带宽也越来越小，但是最窄的情况仍有131 Hz，满足实际需求；同时由波矢虚部的幅值可以知道随着杠杆比的增加纵波在带隙内的衰减能力越来越弱，但是在衰减峰值出却没有这样的规律。

算例二中保持杠杆比α=2不变，考察质量分配对带隙的影响规律。在本文中分别取m=40 g, 30 g, 20 g和ma=10 g, 20 g, 30 g，利用式(15)可以计算得到如图7所示的能带结构。

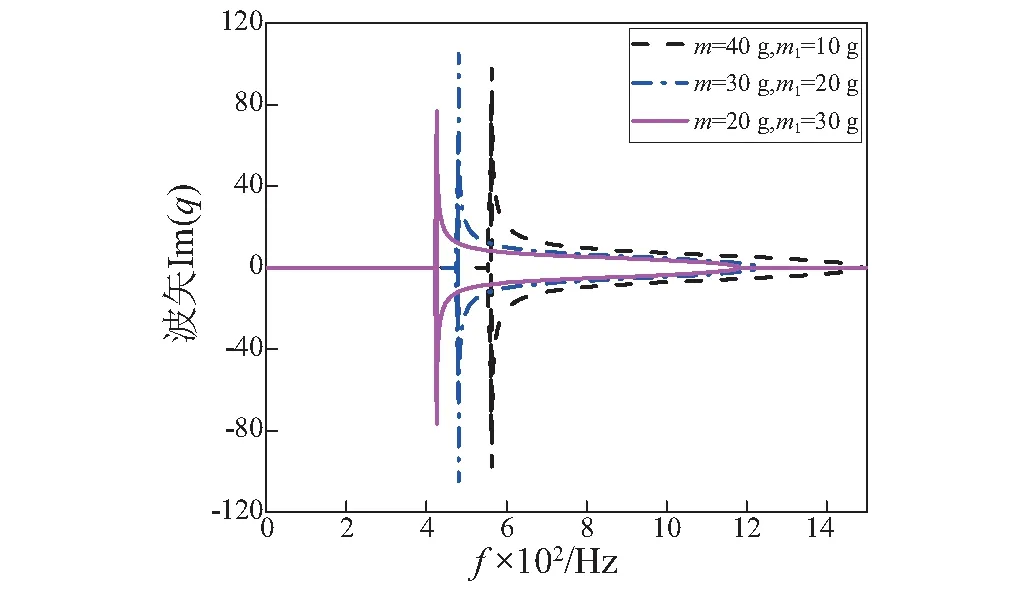
图7 不同质量分配时的能带结构Fig.7 Band structure with different mass assignment

由图7可以看出，质量分配不同时带隙的位置、衰减能力及带隙的宽度都发生了较大的变化：当m=40 g，ma=10 g时的带隙为553～1 488 Hz, 当m=30 g，ma=20 g时的带隙为473～1 228 Hz当m=20 g，ma=30 g时的带隙为421～1 183 Hz。

因此，在实际中要根据需要，可通过灵活地选取杠杆比和质量分配来得到理想的隔振性能。

4 带隙机理解释

通过变换方程式(8)可以得到：共振子的极点、零点分别为

由第二节的结果可以知道，带隙的衰减峰值所对应的频率约为480 Hz。把相同的参数带入极点表达式，得到的共振子极点频率与局域共振带隙衰减峰值对应的频率一致，说明局域共振带隙产生的原因与动力吸振器相似。同时从极点表达式可以看出，当采用相同的参数时，两种共振子的极点频率却不相同，动力反共振结构的极点可以通过调节杠杆比来改变，带隙的位置也将会随之发生改变。由于这个特点使得动力反共振在作为共振子均匀沿杆的纵向周期布置时能够产生初始频率更低的局域共振带隙。

由第二节算例的结果可以看出，在相同的参数条件下，由动力反共振构成的周期结构产生的局域共振带隙要窄于文献[4]中的结果。文献[7]对一维杆的局域共振带隙机理进行了深入研究，分析了共振子参数变化对带隙的影响规律。但本节给出的是在共振子参数给定的条件下，通过定义等效质量和等效刚度两个参数，并比较两种共振子等效参数的差异，给出了造成这一现象的原因。

如上所述，利用式(2)和式(10)定义了如式(16)和式(17)的动力反共振的等效质量和等效刚度。同理，式(18)和式(19)中给出了弹簧质量的等效质量和等效刚度。

(16)

(17)

(18)

(19)

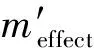
计算时采用第二节中的结构参数，可以得到这两种共振子的等效质量和等效刚度随频率变化的曲线，分别如图8和图9中所示。

图8 两种共振子的等效质量Fig.8 Effective mass of two resonator

由图8和图9的结果可以看出：动力反共振结构的等效参数存在共振峰和反共振峰，而弹簧质量结构的等效参数只存在共振峰值。共振峰值与前述的极点表达式的计算值一一对应，且动力反共振的共振峰值所对应的频率要小于弹簧质量结构的值，从另外一个方面说明了动力反共振结构可以产生初始频率更低的局域共振带隙。而动力反共振结构等效参数中存在的反共振峰值，使得由它所组成的周期结构的局域共振带隙结束的早，即相对文献[4]中的由弹簧质量所组成的一维声子晶体，由动力反共振结构组成的周期结构产生的局域共振带隙要窄。

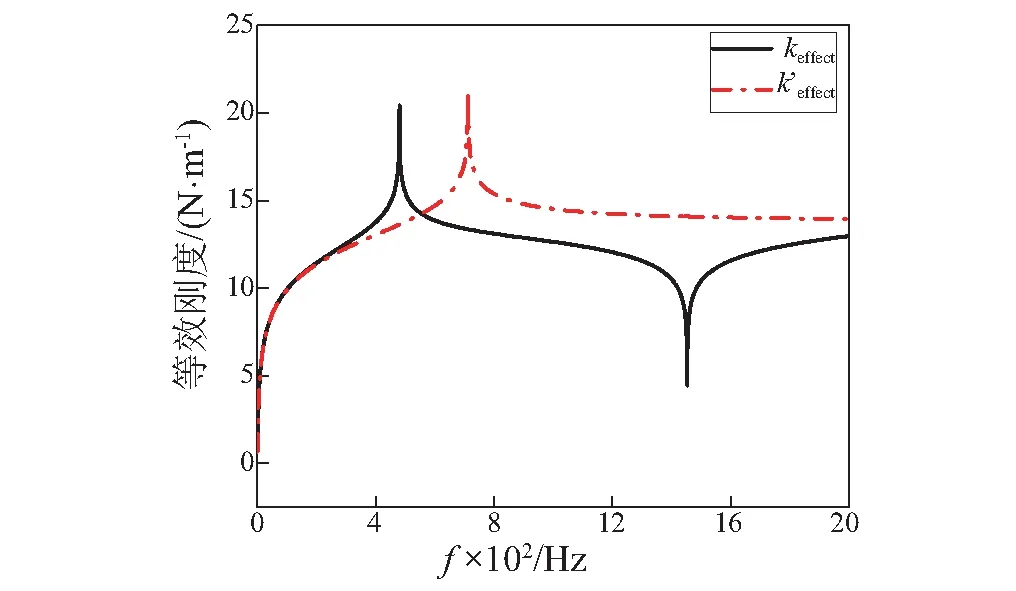
图9 两种共振子的等效刚度Fig.9 Effective stiffness of two resonator

5 结 论

本文提出了一种具有低频局域共振带隙的新型细直梁周期结构，通过能带结构和传输特性的理论与数值研究，主要结论如下：

(1) 基于动力反共振结构的局域共振细直梁，可通过调节杠杆比产生初始频率低的局域共振带隙，且随着周期数目增多，纵向弹性波在带隙内衰减增大。

(2) 在动力反共振保持与文献[4]中振子质量相同的情况下，杠杆比α值越大所产生的局域共振带隙的起始频率越小，且有利于低频隔振，但是带宽会减小。

(3) 在保持杠杆比不变的情况下，动力反共振的悬挂质量ma越大产生的带隙起始频率越小，但同样会减小带隙的宽度。

梁类结构的减振降噪是振动与噪声领域所研究的主要对象之一，本文所采用的动力反共振结构，能够实现小尺寸低频宽带减振，为声子晶体在低频隔振领域的应用，如潜艇轴的纵向隔振，提供了理论基础。

[ 1 ] KUSHWAHA M S, HALEVI P, DOBRZYNSKI L, et al. Acoustic band structure of periodic elastic composites [J]. Physical Review Letters, 1993, 71(13): 2022.

[ 2 ] LIU Z, CHAN C T, SHENG P.Analytic model of phononic crystals with local resonances [J]. Physical Review B, 2005, 71(1): 014103.

[ 3 ] LAI Y, ZHANG Z Q. Large band gaps in elastic phononic crystals with air inclusions [J]. Applied Physics Letters, 2003, 83(19): 3900-3902.

[ 4 ] 王刚.声子晶体局域共振带隙机理及减振特性研究[D].长沙:国防科技大学, 2005.

[ 5 ] LIU Z, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Science, 2000, 289: 1734-1736.

[ 6 ] 郁殿龙.基于声子晶体理论的梁板类周期结构振动带隙特性研究[D].长沙：国防科学技术大学, 2006.

[ 7 ] 肖勇.局域共振型结构的带隙调控与减振降噪特性研究[D].长沙：国防科学技术大学, 2012.

[ 8 ] FLANNELLY W D. Dynamic antiresonant vibration isolator: Patent U S 3322379 [P]. 1967-5-30.

[ 9 ] RITA A D, MCGARVEY J H, JONES R. Helicopter rotor isolation evaluation utilizing the dynamic antiresonant vibration isolator [J]. Journal of the American Helicopter Society, 1978, 23(1): 22-29.

[10] BRAUN D. Development of antiresonance force isolators for helicopter vibration reduction[J]. Journal of the American Helicopter Society, 1982, 27(4): 37-44.

[11] BRAUN D. Vibration isolator particularly of the antiresonance force type: Patent U S 4781363 [P]. 1988-11-1.

[12] IVOVICH V A, SAVOVICH M K. Isolation of floor machines by lever-type inertial vibration corrector[J]. Proceedings of the Institution of Civil Engineers-Structures and Buildings, 2001, 146(4): 391-402.

[13] PLATUS D L. Vibration isolation system: Patent U S 3606233 [P]. 1971-9-20.

[14] YILMAZ C, KIKUCHI N. Analysis and design of passive band-stop filter-type vibration isolators for low-frequency applications[J]. Journal of Sound and Vibration, 2006, 291(3): 1004-1028.

[15] 方俊鑫，陆栋. 固体物理学[M]. 上海：上海科学技术出版社，1980.