模块边界约束条件下产品设计结构矩阵排序算法

卫军朝，张国渊，闫秀天

（1.西北工业大学 机电学院，西安 710072；2.西安电子科技大学 机电工程学院，西安 710071）

0 引言

产生模块化的产品架构是企业满足用户多样性的需求和低成本要求的主要方法之一[1]。模块化设计的一个关键问题是合理地规划具有标准接口的模块，以便高效地配置出不同性能需求的产品[2]。模块识别和定义的一个基本视点是构件之间的耦合性，其准则是模块内部的耦合最大化，模块间的耦合最小化[3～6]。除此之外，模块化还常常需考虑多种基于构件相似性的模块化驱动因素[7～9]。在多目标模块识别之后，产品架构被划分为若干个模块。

面向耦合性的产品设计结构矩阵（DSM）是产品架构的常用建模工具，它不仅可以支持各种聚类算法、辨识产品模块，而且提供直观、紧凑的可视化手段，帮助设计人员更深入地了解产品架构[6,10]。DSM聚类方法主要分为两种，一种是通过对角化DSM或更广义的矩阵来人工划分模块[3～5]，另一种是自动划分算法[7～9]。第一种方法的优点在于对模块大小和边界的设定比较灵活，且具有更好的可视化效果，设计人员可更容易地观察到系统可能存在的分层、交叠结构，其缺点在于不易建立多目标优化模型处理多个模块化驱动目标。第二种方法的优点在于便于建立多目标优化模型，自动生成模块划分方案，但其缺点在于优化结果所对应的结构化DSM并未经过优化排序，影响了DSM的可视化效果。目前很少文献将两种方法相融合在一起。Jung和Simpson[6]提出一种聚类准则，对其优化可得到优化的模块划分方案和构件序列，但该方法并没有涉及相似性模块化驱动目标。

在自动划分算法生成产品模块划分方案之后，为了更清晰地显示出构件间的耦合关系，增强DSM的可视化效果，提出一种模块边界约束条件下的DSM排序优化算法。优化目标是使得紧密耦合的构件尽可能地沿着DSM对角线排列在一起，并且不破坏各模块的边界。采用人工蜂群算法（ABC），对DSM排序聚类准则进行优化。为满足约束条件，开发了新颖的二维食物源编码方式和二维邻域搜索算子。

1 基于ABC的DSM排序算法

人工蜂群算法是一种基于生物群体的元启发算法，它模仿了蜜蜂觅食的行为[11]。ABC算法具有实现简单、参数设置少、优化性能较好等优点，目前已经成功地应用于流水车间调度等复杂离散问题的优化之中[12]。文本算法开发的重点是对排序约束条件的处理。

1.1 DSM排序的聚类准则

对于一个产品系统的DSM，为了使构件之间的耦合近可能地接近DSM的对角线，本文引入文献[3]中所用到的聚类准则，该聚类准则是构件序列θ的函数：

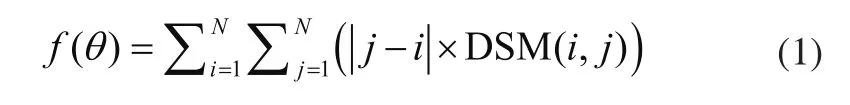
式中N是系统中构件的数目；i和j分别是DSM单元的行指针和列指针。

1.2 解编码

解采用二维数组编码的形式，每一行表示一个已定义的模块，行的排列顺序表示了各模块在排序后的DSM中的排序，而行内构件顺序则表示了各构件在模块中的排序。图1的左边显示了一个由12个构件所组成的DSM在排序之前的标准个体。

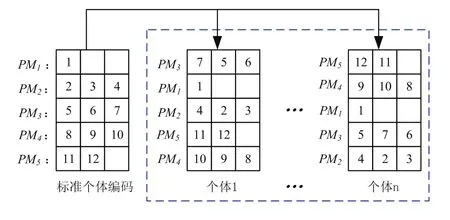
图1 解集合

1.3 随机解生成算子

为了产生初始解集合，以及在侦察蜂阶段随机产生新的解（食物源），需要对标准个体随机排序产生新的食物源。随机解生成算子包含两个阶段。第一阶段对各模块的顺序进行随机打乱，如标准个体的模块顺序（PM1，PM2，PM3，PM4，PM5）被随机打乱后，变为（PM3，PM1，PM2，PM5，PM4）（见图1中的个体1）。第二阶段是对各个模块中的构件进行随机排序，如图1中个体1所示。

1.4 邻域搜索算子

本文提出2种邻域搜索算子：二维两点交叉算子和二维逆序变异算子。二维两点交叉算子应用于ABC算法的雇佣蜂阶段，二维逆序变异算子应用于ABC算法的跟随蜂阶段。

1）二维两点交叉算子

同随机算子类似，二维两点交叉算子也由两个阶段所组成：第一阶段对模块重新排序；第二阶段对模块内构件重新排序，如图2所示。模块重新排序采用两点交叉算子[13]，该算子需要两个解参与，如图3所示。当切割点位置如图3所示时，模块序列由解1（PM3，PM1，PM2，PM5，PM4）变为新解（PM3，PM5，PM1，PM2，PM4）。在第二阶段中，采用概率机制确定一个模块中的构件是否需要重新排序，即若随机数小于一个门槛值Pm，则需重新排序。模块内构件重新排序采用逆序变异算子[14]，如图4所示。

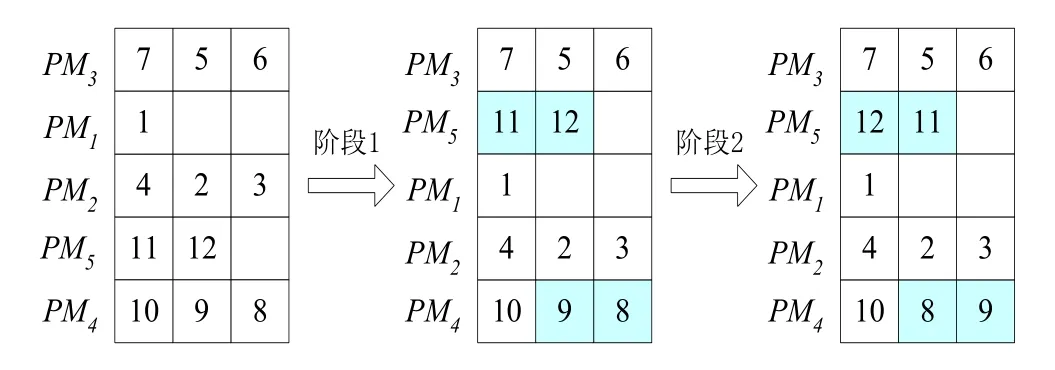
图2 二维两点交叉算子

图3 模块序列的两点交叉算子

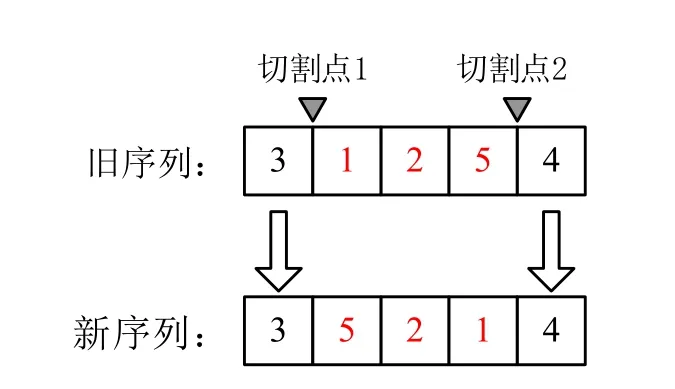
图4 逆序变异算子

2）二维逆序变异算子

二维逆序变异算子也由两个阶段所组成：第一阶段对模块重新排序；第二阶段对模块内的构件重新排序。在两个阶段中，都采用逆序变异算子进行模块或者构件的重新排序，如图4所示。在第二阶段中，同样采用概率机制确定一个模块中的构件是否需要重新排序。

1.5 算法流程

ABC优化方法的总体结构有四部分：初始化阶段、雇佣蜂阶段、跟随蜂阶段、和侦察蜂阶段。其中后三个阶段循环执行，直到循环次数到达最大循环数MCN后程序停止。除了最大循环数MCN，ABC算法所需的控制参数还包括解集合的大小SN以及实验次数上限limit，SN即雇佣蜂或者跟随蜂的数目，limit用于在跟随蜂阶段判断一个解是否需要抛弃。算法流程如下：

算法1：考虑排序约束的ABC排序算法。

输入：DSM，模块划分方案；ABC参数SN，limit和MCN；领域搜索算子的概率选择门槛值Pm。

输出：优化的构件序列。

Step 1：参数初始化：SN, limit，MCN 和Pm。

Step 2：利用随机解生成算子生成初始解集合（食物源）：θk（k=1，2，…，SN）。

Step 3：根据式(1)计算f(θk)，评估每一个解。

Step 4：cycle =1。

Step 5：do。

Step 5.1：使用二维两点交叉算子为雇佣蜂产生新解，计算f（θk）并评估。

Step 5.2：雇佣蜂执行贪心选择过程。

Step 5.3：使用赌轮盘方法选择一个解θk，并且使用二维逆序变异算子为跟随蜂产生一个新解。

Step 5.4：计算f（θk）并评估。

Step 5.5：执行贪心选择过程。

Step 5.6：根据limit值确定被抛弃的解；如果该解存在, 则侦察蜂用一个随机产生的解来代替被抛弃的解。

Step 5.7：记住到目前为止的最优解。

Step 5.8：cycle = cycle+1。

Step 6：while cycle ≤ MCN。

2 实例分析

本文采用文献[7]中的无绳手持吸尘器作为研究案例，该产品由Black and Decker公司生产，型号为CHV1210。CHV1210被分解为57个构件，图5是对应的DSM矩阵，字母编码表示了两个构件之间的耦合关系类型，使用下面的缩写形式：Attachment（连接），Dust flow （尘土流），Force （力），Spatial relation （空间关系），fLow of air（空气流），Heat rejection （热排放），mechanical torQue（力矩）和Electrical energy（电能）。在DSM聚类计算时，所有这些字母都被数值1所代替。

对文献[7]中的一种模块划分方案进行对角化处理。该方案的生成同时考虑了耦合性和相似性，方案的定义见图5中的R01～R12。

ABC优化算法的参数设置为：SN=50；limit=150；MCN=500；Pm=0.7。算法在Matlab R2010b（The MathWorks，Natick，Massachusetts，USA）的平台上开发，运行算法的计算机配置为：Intel® Core™i3-2350M CPU（2.3 GHz），2GB RAM。算法运行时间约为43s。优化后的聚类准则为654，得到的DSM如图6(a)所示。

与原始的DSM相比较，图6(a)更清晰地显示出各模块/构件之间的耦合关系。1）更清晰地显示出关系紧密的模块。如原本不相邻的模块R02和R08之间有着较多的耦合，它们被排列在了一起。2）显示出模块内部结构化组织。如模块R02的构件在优化排序后明显地划分为了2个子模块：{17,18,21,19,12,13,16}和{14,20,15}。{17, … ,16}是喷嘴部分的构件集合，它与系统中的其他模块之间的耦合关系很少；{14,20,15}是灰尘吸纳器的构件集合，它与R08之间有着强的耦合。3）更清晰地显示出影响若干模块设计的关键构件。关键构件与所属模块的其他构件有着较多的耦合，同时又与多个其他模块有着耦合关系，对其进行设计和再设计往往会影响到多个模块。经过优化排序，紧密耦合的若干模块尽可能地排列在一起，因此，这些关键构件便更清晰地显现出来。如主腔体模块R01中的构件1（左壳）和2（右壳）不仅是R01的总线构件，也是模块R01与模块R09和R05之间的接口构件。构件35（结构手柄）不仅是模块R05的核心构件，而且是模块R05与R01、R07、R03之间的接口构件。

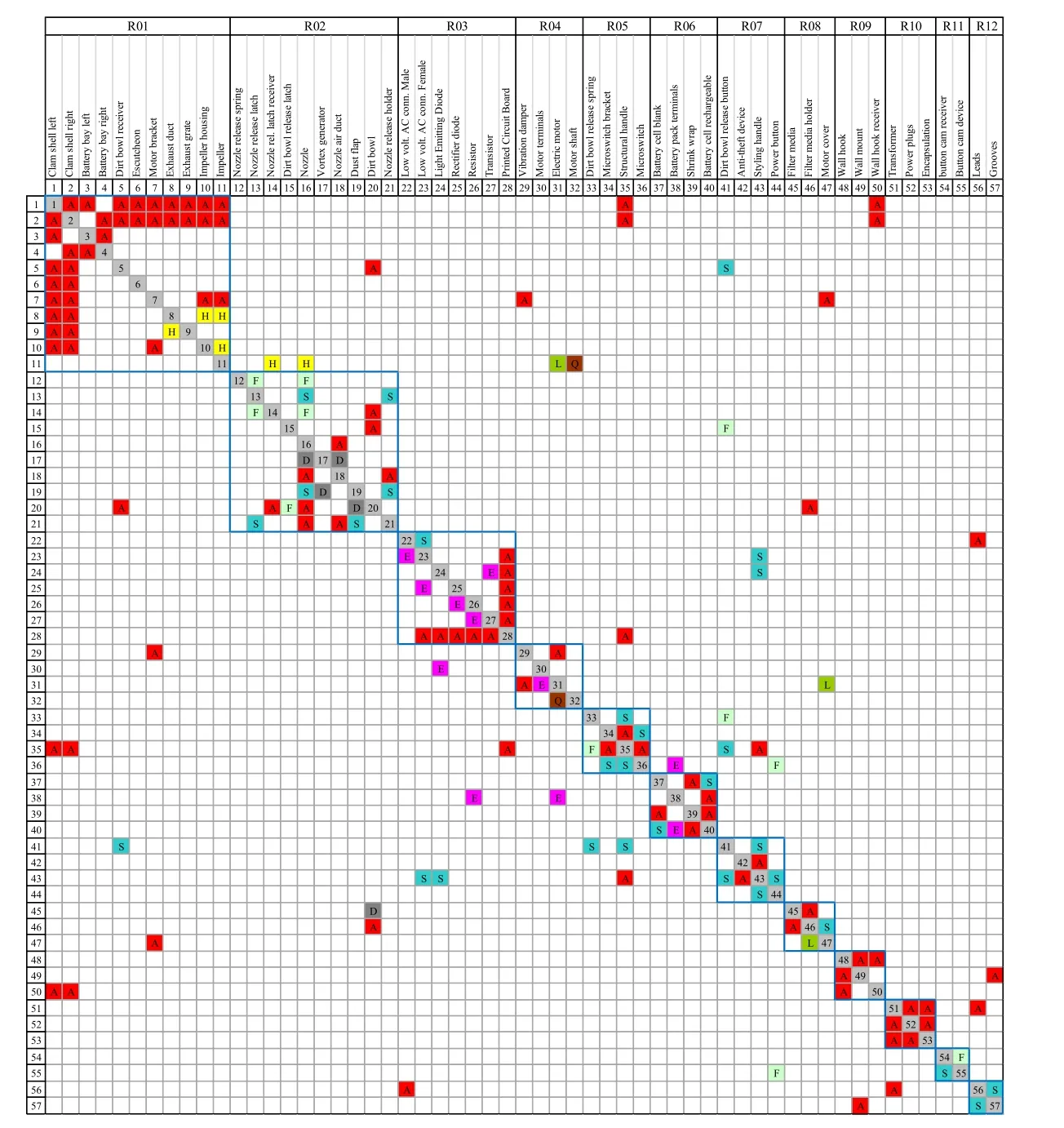
图5 CHV1210的DSM[7]

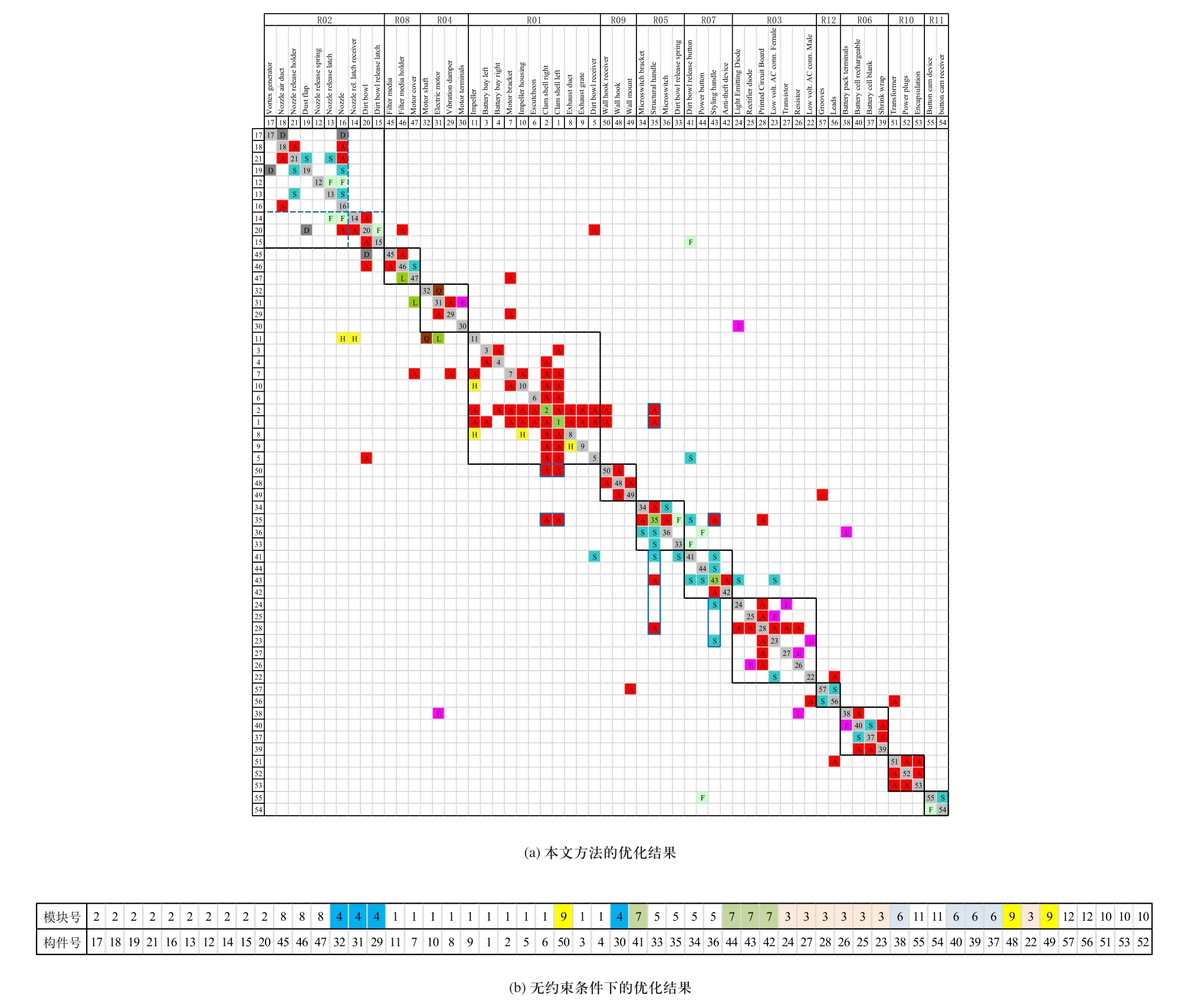
图6 DSM优化排序结果

在无约束条件下对本案例中的DSM进行对角化，得到的构件排序结果如图6(b)所示。图中有多个模块的边界被打破，如模块R04、R09等。这便为设计人员直观地分析模块/构件之间的耦合关系带来了不便。如在图6(a)中很容易辨识出模块R09是一个链式结构（50-48-49），而在图6(b)的构件序列中，R09的构件50与构件48、49相距较远，R09的架构特点并不容易直观地辨识出来。为满足约束条件需对图6(b)的排序结果进行人工调整，其过程非常繁琐，设计人员需要不断地评估构件的新序列是否优化。

3 结论

为了使DSM更清晰地显示出模块/构件之间的耦合关系，帮助设计人员更深入地了解产品架构，提出一种预定义模块边界约束条件下的DSM排序优化算法。该算法不破坏模块的边界，将紧密耦合的模块尽可能地排列在一起，同时对模块内的构件进行排序，将紧密耦合的构件尽可能地放置在一起，避免了无约束排序算法后繁琐的人工排序过程。

[1]Simpson TW, Maier J R A,Mistree F.Product platform design: method and application[J].Research in Engineering Design,2001,13(1):2-22.

[2]Ericsson A E G.Controlling design variants: modular product platforms[M].New York:ASME Press,1999.

[3]汪文旦,秦现生,阎秀天,白晶.一种可视化设计结构矩阵的产品设计模块化识别方法[J].计算机集成制造系统,2007.13(12):2345-2350.

[4]Daie P, Li S. Matrix-based hierarchical clustering for developing product architecture[J].Concurrent Engineering-Research and Applications,2016,24(2):139-152.

[5]Sarkar S,Dong A,Henderson J A,et al.Spectral characterization of hierarchical modularity in product architectures[J].Journal of Mechanical Design, 2013,136(1): 249-256.

[6]Jung S, Simpson T W.New modularity indices for modularity assessment and clustering of product architecture[J].Journal of Engineering Design,2017,28(1):1-22.

[7]Borjesson F, Hölttä-otto K. A module generation algorithm for product architecture based on component interactions and strategic drivers[J].Research in Engineering Design, 2014, 25(25):31-51.

[8]李中凯,千红涛.环境意识模块化产品体系结构的设计优化方法[J].计算机辅助设计与图形学学报,2015,27(1):166-174.

[9]魏巍,许少鹏,梁赫.基于环境资源因子的产品平台模块划分方法[J].计算机辅助设计与图形学学报,2016,28(2):335-344.

[10]EPPINGER S D, BROWNING T R. Design structure matrix methods and applications[M]. Cambridge:MIT Press,2012.

[11]Karaboga D, Gorkemli B, Ozturk C, et al.A comprehensive survey: artificial bee colony (ABC) algorithm and applications[J].Artificial Intelligence Review, 2014, 42(1):21-57.

[12]张培文,潘全科,李俊青,等.有限缓冲区流水车间调度的混合人工蜂群算法[J].计算机集成制造系统,2013,19(10):2510-2520.

[13]Murata T, Ishibuchi H. Performance evaluation of genetic algorithms for flowshop scheduling problems[A].Proceedings of the First IEEE Conference on Evolutionary Computation[C],1994:812-817.

[14]Fogel D. A parallel processing approach to a multiple travelling salesman problem using evolutionary programming[A].Proceedings of the Fourth annual Symposium on Parallel Processing, Fullerton,CA,USA[C],1990:318-326.