下肢康复训练机器人设计及分析

（湖北文理学院 机械与汽车工程学院，襄阳 441053）

0 引言

随着机器人技术的快速发展，机器人在人类生活中的应用也越来越广泛[1]。康复机器人越来越成为研究的热点问题。在康复领域，对于由于疾病或者其他原因导致的下肢活动障碍人群，机器人的介入无疑是一个减轻康复负担的优选。根据患者在康复训练中的身体姿态，下肢康复机器人可分为四类，即坐/卧式下肢康复机器人、直立式下肢康复机器人、辅助起立式康复机器人和多体位式康复机器人[2]。

欧美国家对康复机器人研究开展的较早，结合康复医学展开了很多研究，取得了显著的成果，并在实际的应用中取得了良好的效果。国内以清华大学、哈尔滨工程大学、燕山大学、上海交通大学等为代表，对下肢康复机器人进行了关键技术的研究，并取得了一系列比较有价值的研究成果[3～6]。

图1 腿部模型的坐标系

针对下肢康复机器人，本文结合人体工程学的相关标准，根据人体关节尺寸和转角范围确定了合理的机器人机构转角范围，基于人体下肢踝关节的运动空间确定机器人机构的杆长参数。运用D-H法建立了机构的运动学正解和逆解，并基于Matlab工具箱验证了推导的运动学模型的正确性。本文的研究成果将为所设计的下肢康复机器人控制和轨迹规划提供重要参考。

1 下肢康复机器人设计

1.1 定机构参数（杆长、转角范围）

为了确定下肢康复训练机器人机构参数和转角范围，先进行腿部的运动学建模及工作空间分析；人体下肢主要包括大腿、小腿、足部及连接各部分的髋关节、膝关节和踝关节，只考虑到踝关节处，建立如图1所示的腿部模型的坐标系。基于D-H法建立腿部模型的运动学模型，各个关节的转角范围：髋关节转角θ1为10～100°，膝关节转角θ2为0～140°。

利用Simulink和Simmechanics工具箱建立腿部的机构模型（如图2所示），通过仿真分析，借助于绘图仪来显示腿部踝关节的工作空间，如图3所示。

借助于Simulink和Simmechanics工具箱搭建腿部模型和机器人机构模型的联合仿真模型，如图4所示。

图2 腿部的机构模型

图3 踝关节的工作空间

通过给腿部模型的各个关节施加转角范围，腿部模型的转角范围如图5所示。仿真可以得到下肢康复机器人机构的各个关节的转角范围如图6所示。

通过仿真的结果确定下肢康复训练机器人的转角范围，结合机构的坐标系分布情况，给出工作状态下各关节的运动范围为：

关节转角范围：

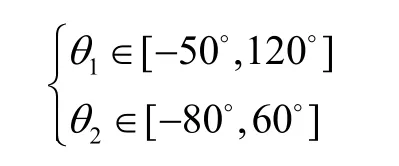
1.2 运动学分析

图4 腿部模型和机器人机构联合模型

图5 腿部关节的转角

图6 机构模型关节的转角

根据联合仿真的结果确定机器人机构的杆长、关节转角范围，基于D-H法建立两杆机构的运动坐标系，坐标系如图7所示。

利用相邻坐标系之间的转换矩阵可以得到该下肢康复机器人机构的运动学正解，此处不再赘述。

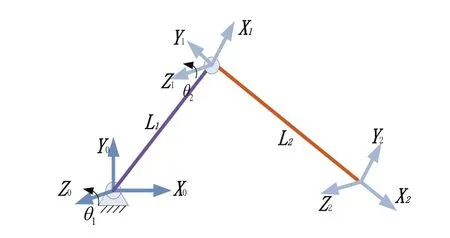
图7 机器人机构坐标系

关节坐标系2（机构末端坐标系）到关节坐标系1的坐标变换为

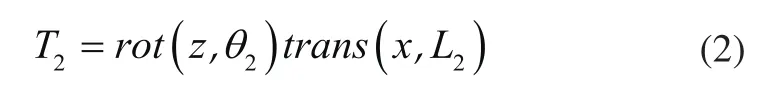
关节坐标系2（机构末端坐标系）到基础坐标系0的坐标变换矩阵为：

通过Matlab中的Simulink与SimMechanics工具箱模块分别搭建下肢康复训练机器人的运动学正解仿真模型与机构仿真模型，如图8所示。本过程的仿真思路为：将机构各关节变量分别输入Simulink运动学仿真模块与SimMechanics机构仿真模块，得到各自末端位姿参数输出值，对二者的位姿输出分别进行差值处理，得到运动学正解模型输出与机构仿真模型输出之间的关于机构末端的位姿误差，若误差出现在允许范围内，则证明运动学模型是正确的。

图8 机器人机构运动学正解验证模型

末端控制点的位置参数分别Px、Py、Pz，姿态参数分别为α、β、γ。仿真结果显示（如图9、图10所示），机构运动学正解模块末端位姿输出值与机构模型输出值基本保持一致，其中位置输出值最大误差数量级为10-13mm，姿态输出值最大误差数量级为10-14，误差值较小，对机器人的精度不会造成影响，可以忽略。因此认为运动学正解仿真模块与机构仿真模块所对应的机器人末端位姿输出值相同，仿真结果证明机构运动学正解模型是正确的。

移民是中国古代社会重要的事件，且代有相沿。由于今日民系格局大多肇始于南宋，故表1选取了南宋以来几次重大的移民事件进行梳理[13]。

图9 位置误差曲线

图10 姿态误差曲线

利用Simulink和Simmechanics工具箱建立康复训练机器人的机构模型，通过仿真分析，借助于绘图仪来显示机器人二杆机构末端的作业空间，如图11所示。

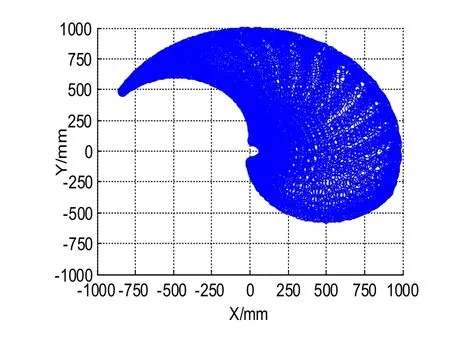
图11 机器人机构末端的作业空间

为求出机器人机构末端位置矢量相对于第一主动关节坐标系x2y2z2的逆解，令末端工具坐标系相对于自身基座坐标系的位姿矩阵为T，并设之为：

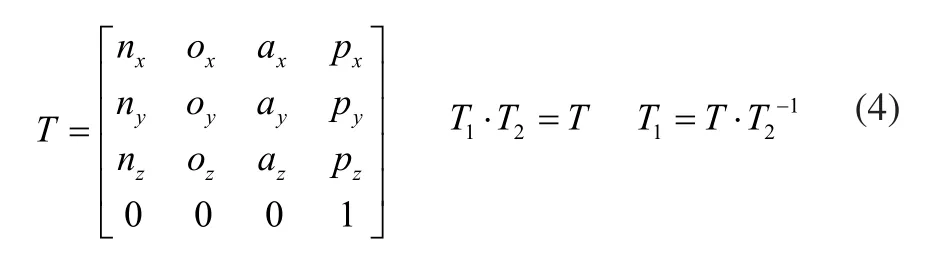
得到下肢康复机器人机构的运动学逆解为：

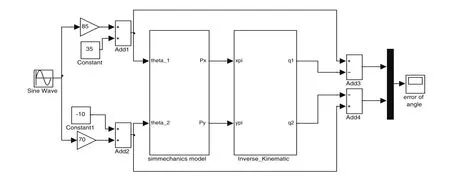
图12 机器人机构运动学逆解验证模型

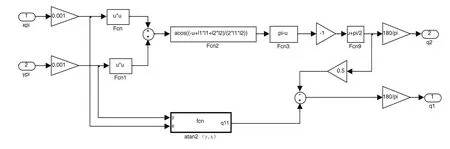
图13 Inverse_Kinematic模块封装

通过Matlab中的Simmulink和SimMechanics工具箱分别搭建运动学逆解仿真模块和机构仿真模块，以机构末端位姿参数为中间媒介，建立正、逆解模块间的关系，如图12所示。将机器人各关节变量输入到SimMechanics机构仿真模块，测得机器人末端位姿参数，将其代入Simmulink运动学逆解仿真模块，进一步求得逆解模型下的机器人各关节变量参数。通过对比运动学逆解模型求得的各关节变量输出参数与机构模型各关节变量初始输入参数，得到运动学逆解模型输出值相对于理论值的误差情况，若误差出现在允许范围内，证明运动学逆解模型是正确的。

其中Inverse_Kinematic模块内封装如图13所示。

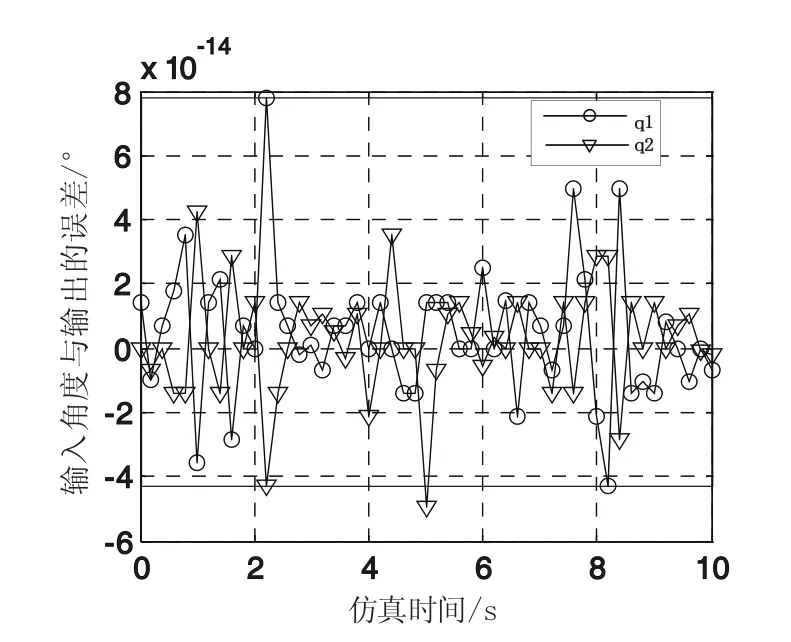
图14 输入角度与输出的误差曲线

仿真结果显示（如图13所示），运动学逆解模型所求出的机构关节变量与给定输入下的关节变量间的差值在10-14数量级，误差较小，因此仿真结果证明所求取的运动学逆解模型是正确的。

1.3 动力学模型的建立

图15 机器人机构的受力分析

根据动能和势能的定义，连杆1的动能K1和位能P1为：

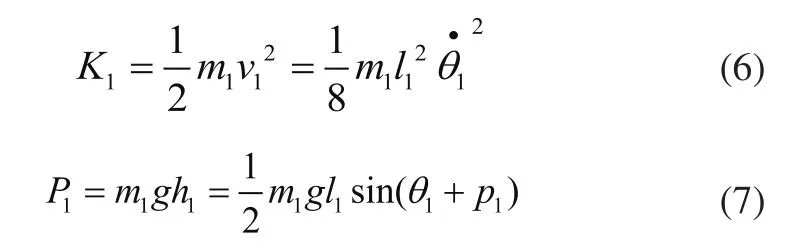
连杆2质心点坐标为：

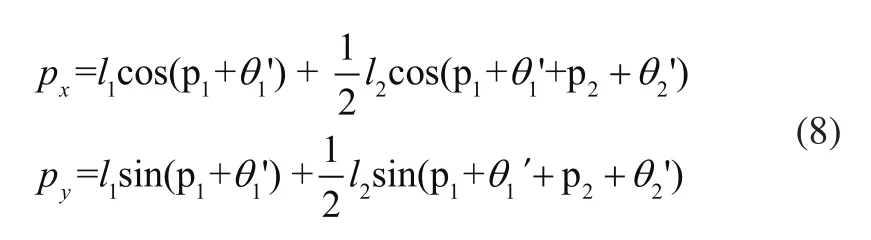
得到连杆2的动能K2和位能P2为：

所以机器人机构的总动能和总位能分别为：

【】【】

采用拉格朗日法建立机器人机构的动力学模型：

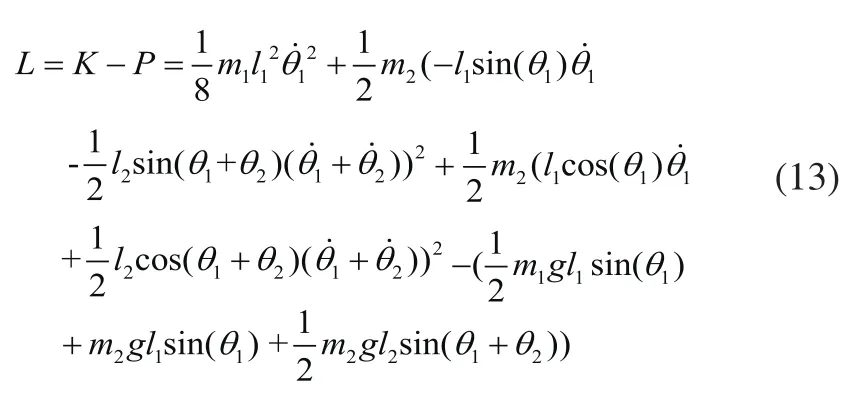
基于刚体的拉格朗日动力学方程可以得到：

设转动杆的驱动力矩为T1，T2。考虑粘滞摩擦系数的情况下，下肢康复机器人机构的动力学方程为：

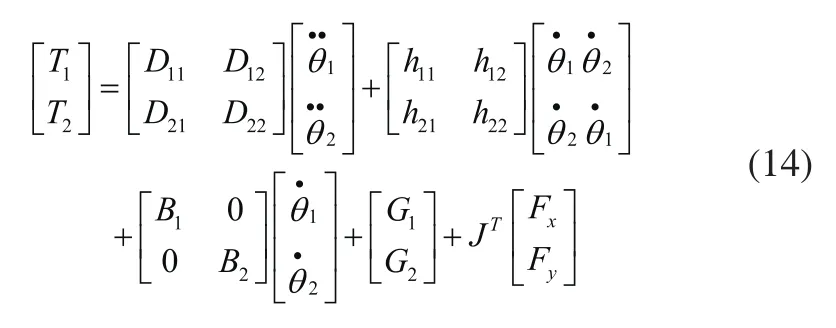
其中雅克比矩阵为：

2 结论

本文根据人体工程学相关标准确定设计的下肢康复机器人的关节转角范围，利用腿部踝关节的工作空间确定机器人机构的杆长参数。并基于D-H法建立了下肢康复机器人的运动学正解和运动学逆解，通过Simulink和SimMechanics工具箱搭建机器人机构模型，与理论解进行对比验证了机器人运动学模型的正确性；采用拉格朗日法，建立下肢康复训练机器人的动力学模型。搭建的运动学和动力学模型为实验样机的控制和轨迹规划提供了重要基础。下一步将针对根据确定的机器人机构参数研制原理样机，并进行相关的运动规划与控制研究。

[1]史小华,王洪波,孙利,等.外骨骼型下肢康复机器人结构设计与动力学分析[J].机械工程学报,2014,50(03):41-48.

[2]李纬华,孙洪颖.下肢康复机器人人机运动分析及仿真研究[J].机电工程技术,2016,45(08):24-27.

[3]张立勋,王克义,张今瑜.下肢康复训练机器人的运动协调仿真[J].机械设计与研究,2007,23(06):46-50.

[4]高宏,刘相权,米洁,等.下肢康复训练机器人机构运动分析与仿真[J]. 机械制造与自动,2015,44(06):107-109.

[5]李军强,王娟,赵海文,等.下肢康复训练机器人关键技术分析[J].机械设计与制造,2013,9:220-223.

[6]王勇,张英,刘正士.下肢康复机器人的设计与仿真分析[J].华中科技大学学报(自然科学版),2011,39:252-254.

[8]杨俊友,李宇庆,白殿春.下肢康复机器人机械结构设计与动力学仿真[J].沈阳工业大学学报,2010,32(5):514-519.

[9]李醒,王建辉,方晓柯.五自由度上肢康复机器人动力学建模及仿真[J].控制工程,2012,19(05):823-831.