加入不确定扰动的无人机飞行轨迹跟踪控制

张晓军，陆兴华

(广东工业大学华立学院，广东 广州 511325)

0 引 言

无人机作为一种新型的无人驾驶飞行器，因其具有机动性好、隐身性强、全天候遂行任务能力强等特点，在执行危险军事任务、情报侦查、探险救援等方面展示了较好的应用价值。无人机按照应用种类可以分为无人直升机、无人固定翼机、无人多旋翼飞行器等，具有较好的高空突防性和低空机动性，在军事和民用等领域都具有广泛的发展前景。无人机由于体积较小、质量较轻，在受到强对流气流扰动下，容易产生飞行失稳，出现航向偏移，容易导致飞行事故的发生。需要在不确定的气流扰动下进行无人机的飞行轨迹跟踪控制，提高飞行稳定性，研究在不确定气流扰动下的无人机飞行轨迹跟踪控制算法具有重要意义。

在无人机飞行轨迹跟踪控制系统设计中，关键的技术是在扰动作用下构建无人机的飞行动力平衡数学模型，根据对无人机在干扰作用下的阻尼力矩分析和稳态误差补偿控制，实现不确定气流扰动下的轨迹跟踪和修正，提高飞行稳定性。传统方法中，对无人机的飞行轨迹跟踪控制算法主要有基于模糊神经网络控制的飞行轨迹误差修正和跟踪算法、增益调度算法、大扰动作用下的姿态角消颤控制算法等[1-3]。文献[4]提出一种基于变结构自适应理论的无人机飞行轨迹跟踪控制算法，采用模糊PID控制思想，对飞行轨迹中受到的气流扰动误差进行自适应修正，对神经网络采用变结构多线程跟踪控制设计实现姿态角惯导控制，提高了无人机飞行稳定性；但是该算法计算开销较大，控制的实时性不好，容易导致稳态误差漂移失真。文献[5]提出一种基于不确定边界的自适应神经网络控制的无人机飞行气流扰动抑制和飞行轨迹跟踪控制算法，结合小扰动原理和Lyapunov稳定性原理进行扰动抑制，提高了飞行轨迹的振荡拟合性和飞行控制的稳健性；但是该方法采用能量反演镇定函数非线性跟踪，随着扰动气流不确定性的增强，对飞机的惯导失衡补偿性能不好。文献[6]采用滑膜同步协调控制方法，飞行参数的自整定性能受到扰动气流的误差漂移影响较大，控制性能不好。

针对上述问题，文中提出一种基于多传感信息的自适应融合跟踪误差补偿的不确定气流扰动下无人机飞行轨迹跟踪控制算法。首先进行了无人机飞行轨迹跟踪控制的约束参量分析和飞行动力学模型构建，采用多传感信息飞行姿态数据采集和融合方法进行控制器设计，通过自适应融合跟踪误差补偿实现无人机飞行轨迹跟踪控制算法改进，最后通过仿真实验进行了性能验证。

1 无人机飞行轨迹跟踪控制对象描述和飞行动力学模型构建

1.1 无人机飞行轨迹跟踪控制对象描述

无人机在不确定气流扰动下，容易产生飞行轨迹偏移，通过无人机飞行轨迹跟踪控制，提高了无人机的飞行稳定性。无人机飞行轨迹跟踪控制具有运动参数的时变性、参数自整定性等特点，为了实现对无人机飞行轨迹跟踪控制，首先进行控制对象的数学模型构建[7-10]，采用一个非光滑自治时滞的二自由度微分方程描述无人机飞行轨迹跟踪控制的控制对象模型：

(1)

其中，d(t)为无人机飞行状态下的振荡阻尼函数；x(t)为无人机飞行跟踪控制的时滞；A、B为飞行稳态平衡点的约束参量系数，表示为一个适当维数的系统矩阵。

在不确定扰动气流下，无人机出现振荡特性，对飞行系统的稳定性产生振荡幅度和频率方面的影响，在固定的振荡时间下，采用多传感器量化融合采集方法进行飞行姿态数据采集，在多传感器融合下，飞行轨迹跟踪控制的量化跟踪问题可以描述为如下迭代方程形式：

x(k+1)=A(k)x(k)+Γ(k)w(k)

(2)

zi(k)=Hi(k)x(k)+ui(k),i=1,2,…,N

(3)

其中，x(k)∈Rn×1为无人机纵向飞行运动的状态；A(k)∈Rn×n为状态转移矩阵；假设w(k)为无人机受到的不确定气流扰动项，是均值为零且方差为Q(k)的高斯白噪声；Γ(k)为飞行状态失衡下的线性化小扰动修正驱动矩阵；zi(k)∈Rp×1为第i个传感器对无人机飞行姿态信息的测量值；Hi(k)∈Rp×n为多传感器阵列对无人机飞行姿态信息相应的测量矩阵；ui(k)∈Rp×1为多传感器阵列对无人机飞行姿态数据的测量噪声，且是均值为零、方差为Di(k)的高斯白噪声。

无人机在受到不确定气流扰动中，假定气流扰动的噪声w(k)与ui(k)之间，以及多传感器阵列对无人机飞行姿态数据测量误差之间均相关，即

(4)

无人机飞行姿态控制向量在时间t的状态向量能有效反应无人机飞行轨迹的小扰动变化，此时飞行轨迹跟踪的时滞约束条件为：

(5)

根据上述描述，构建了无人机飞行轨迹跟踪控制对象，以此为基础进行无人机飞行运动的动力学分析和飞行轨迹跟踪控制器设计。

1.2 加入不确定气流下无人机飞行动力学分析

通过对无人机加入不确定气流下的飞行动力学运动分析，进行控制器优化设计。无人机飞行轨迹跟踪控制是一个多参量融合的闭环控制系统，飞行轨迹跟踪控制中的飞行动力学模型包含了多个平衡点，在有限时间稳定条件下，随着不确定气流扰动的增强[11]，无人机的飞行过程中通常采用传递函数分析方法，可得无人机纵向飞行动力学传递函数为：

(6)

对于上述模型的分析可知，无人机在不确定气流扰动下飞行中受到的扰动误差为一个多输入单输出形式，根据线性系统理论，在零初始条件下，对无人机飞行动力学传递函数进行拉普拉斯变换，可得飞行轨迹跟踪控制的输出传递函数为：

(7)

对上式的系数进行单独求解，把无人机受到的扰动气流分解为确定部分和不确定部分，得到飞行纵向运动参数的状态反馈控制模型为：

uc(t)=Kxc(t)

(8)

引入强跟踪滤波思想[12]，力矩平衡状态时的线性增益Δi(k,r)能通过在k时刻第i个测量值进行量化分解得到，无人机飞行的稳态特征信息通过动静力特征分解，得到的无人机飞行的稳定性状态方程描述为：

(9)

E[V(k)VT(k)]=

(10)

根据上述模型，计算无人机侧向运动在纵向坐标平面的第r(r=1,2,…,p)个分量的量化步长。根据上述对无人机的飞行动力学数学模型构建，得到无人机轨迹跟踪控制的运动状态特征系数满足：

(11)

根据飞行流体动力和力矩的稳定性误差补偿原理，得到无人机在飞行轨迹跟踪的闭环增益具有反馈控制性能，基于多传感信息的自适应融合跟踪误差补偿方法进行反馈控制，实现飞行轨迹的自适应跟踪控制改进算法设计。

2 无人机飞行轨迹跟踪和稳定性控制优化设计

2.1 多传感信息的自适应融合跟踪误差补偿方法描述

在上述无人机飞行运动的动力学数学模型构建和被控对象描述的基础上，进行无人机飞行轨迹跟踪和稳定性控制优化设计。文中提出基于多传感信息的自适应融合跟踪误差补偿的飞行轨迹跟踪控制方法，在有限时间域内，分析飞机在受到不确定气流扰动下的飞行轨迹控制跟踪参量模型满足：

(12)

用多个连续时滞非光滑系统对无人机的定常运动进行运动平衡分解，飞行轨迹跟踪控制系统x(t)在初始时刻d1(t)和d2(t)的俯仰力矩和推力矩相平衡的目标状态方程为：

(13)

采用多传感信息的自适应融合跟踪补偿，将飞行轨迹跟踪控制目标函数描述为：

(14)

其中，x(k)∈Rp表示无人机在俯仰飞行段的摆舵角状态；u(k)∈Rq表示无人机在横滚侧向飞行的应力特征值；z(k)∈Rm表示无人机在受到不确定气流扰动的动静力平衡状态矩阵(变量p,q,m为正整数)；A,B,C为多传感器信息融合矩阵。

对多传感器阵列采集的无人机飞行轨迹跟踪控制姿态数据样本集进行线性化拟合：

S={(x1,x1),…,(xl,xl)}

(15)

在纵向等速水平直线飞行下，无人机飞行处于理想的平衡状态，飞行轨迹跟踪该控制的小扰动判别式为：

(16)

多传感信息的自适应融合跟踪过程为一个非线性小扰动的时滞误差补偿过程，将受扰动的各个参数代入系统控制传递函数中，然后再通过多传感信息的自适应融合跟踪误差补偿，进行飞行轨迹的误差修正和跟踪。

2.2 无人机飞行轨迹跟踪控制算法改进实现

在不确定气流扰动下，采用自适应律进行无人机飞行轨迹的姿态角跟踪，对于时滞函数d1(t)和d2(t)，根据Lyapunove泛函[13]，飞行轨迹鲁棒性跟踪控制的稳定解满足：

0≤d1(t)≤h1<∞,0≤d2(t)≤h2<∞

(17)

(18)

其中，h1,h2,τ1与τ2为正常量，引入横舵纵倾振荡向量进行飞行轨迹跟踪的基准运动方程闭环控制。

通过量化信息评价，无人机飞行轨迹跟踪控制的品质评价系数满足：

(19)

(20)

那么，平衡点异变非光滑，根据李雅普诺夫稳定性理论可知，当Lyapunove函数满足如下条件时[14]，系统在有限时间内渐近稳定。

R1≥R2≥0,Z1≥Z2>0,Z3>0

(21)

在连续有限的时间域内，根据链法则特性，对无人机飞行轨迹的姿态参量全部量化信息进行自适应参量估计。

得到的估计结果为：

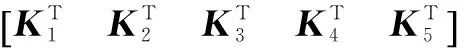
(22)

(23)

(24)

当无人机飞行轨迹跟踪的多传感信息满足下列的全局有限时间收敛等式，飞行轨迹跟踪控制的误差收敛到零：

(25)

(26)

(27)

(28)

(29)

其中：

(30)

如果误差协方差特征向量Ψ(d1(t),d2(t))<0,有：

(31)

根据Lyapunove稳定性原理，采用文中方法进行无人机飞行轨迹跟踪控制是渐进稳定的，系统的动态品质较好。通过上述算法设计，采用多传感信息的自适应融合跟踪误差补偿，实现了在不确定气流扰动下的飞行轨迹跟踪控制和误差修正补偿，其普适性较强。

3 仿真实验与结果分析

为了测试该算法在实现无人机飞行轨迹跟踪控制中的性能，对其进行仿真实验。实验开发软件为Matlab 7,采用多传感器VXI总线技术进行无人机飞行姿态数据采集，选择ADI公司的ADSP-BF537作为数字处理芯片，进行飞行控制系统的数字信号处理。采用三轴电子罗盘LSM303DLH(含加速度计和磁力计)和L3G4200D陀螺仪组成的无人机飞行轨迹姿态信息采集模块嵌入到无人机控制系统，实现飞行轨迹和姿态信息的原始数据采样。假设无人机飞行的初始速度为290 m/s，初始高度为10 000 m，初始姿态角为0°，俯仰角在最陡下滑角度从0°增加到32°，无人机在经历一定的横滚飞行之后，以俯仰角12°进行水平飞行。根据上述仿真环境和参数设定，进行飞行轨迹跟踪控制仿真，将无人机飞行的控制纵向平面抽象为图1所示的栅格模型。

图1 无人机飞行平面格栅模型

如图1所示，无人机飞行轨迹的起始点为[10,210]、终点为[300,3 000]，环境中的起点和目标点固定，受到的不确定扰动气流的强度变化范围为-10～0 dB，在此基础上获得飞行轨迹，并进行轨迹跟踪控制，得到整个飞行轨迹路径上的飞行轨迹跟踪路径仿真结果，如图2所示。

从图2可见，采用文中方法进行无人机的飞行轨迹跟踪控制，通过对多传感信息的自适应融合跟踪误差补偿，在不确定的气流扰动下能有效实现对航向误差的自适应修正，提高了飞行轨迹跟踪控制的精度，保证了飞行稳定性。为了定量对比性能，与传统方法进行比较，以飞行轨迹跟踪控制的预测误差为测试指标，得到的仿真结果如图3所示。

从图3可见，采用文中方法进行飞行控制，轨迹跟踪的预测误差能准确收敛到零，振荡较小，性能优于传统方法。

4 结束语

无人机由于体积较小、质量较轻，在受到强对流气流扰动下，容易产生飞行失稳，出现航向偏移。文中提出一种基于多传感信息的自适应融合跟踪误差补偿的不确定气流扰动下无人机飞行轨迹跟踪控制算法。首先进行了无人机飞行轨迹跟踪控制的约束参量分析和飞行动力学模型构建，采用多传感信息飞行姿态数据采集和融合方法进行控制器设计，通过自适应融合跟踪误差补偿实现无人机飞行轨迹跟踪控制算法改进。研究表明，采用该方法进行无人机飞行轨迹跟踪控制的精度较好，误差快速收敛到零，提高了无人机飞行中对不确定气流扰动的抗干扰性和稳健性，保障了飞行稳定。

图2 无人机飞行轨迹跟踪控制仿真结果

图3 控制性能对比

[1] ZHANG J F,HAN Z Z,WU H.Robust finite-time stability and stabilization of switched positive systems[J].IET Control Theory and Applications,2014,8(1):67-75.

[2] NGOC P H A.Stability of positive differential systems with delay[J].IEEE Transactions on Automatic Control,2013,58(1):203-209.

[3] 李煜琦,邵珠峰,田斯慧,等.基于吊丝配重的空间机械臂零重力模拟装置卸载率分析及评价[J].机器人,2016,38(3):293-300.

[4] 王 勋,张代兵,沈林成.一种基于虚拟力的无人机路径跟踪控制方法[J].机器人,2016,38(3):329-336.

[5] MAHBOUBI H,MOEZZI K,AGHDAM A G,et al.Distributed deployment algorithms for efficient coverage in a network of mobile sensors with nonidentical sensing Capabilities[J].IEEE Transactions on Vehicular Technology,2014,63(8):3998-4016.

[6] 章 俊,张冬梅,王辛刚.一类参数不确定连续正系统受限控制[J].信息与控制,2015,44(5):592-597.

[7] 朱 熠，陈 欣，李春涛，等.风扰动下的飞翼无人机静态投影控制[J].兵工学报,2015,36(7):1237-1246.

[8] 雷旭升,陶 冶.小型无人飞行器风场扰动自适应控制方法[J].航空学报,2010,31(6):1171-1176.

[9] 刘 重，高晓光，符小卫，等.基于反步法和非线性动态逆的无人机三维航路跟踪制导控制[J].兵工学报,2014,35(12):2030-2040.

[10] 徐为民,徐 攀.不确定扰动下双起升桥吊双吊具鲁棒自适应滑模同步协调控制[J].控制与决策,2016,31(7):1192-1198.

[11] 葛立志.基于全弹道控制分析的水下航行器攻击模型视景仿真[J].舰船电子工程,2015,35(3):137-141.

[12] 刘 恒,李生刚,孙业国,等.带有未知非对称控制增益的不确定分数阶混沌系统自适应模糊同步控制[J].物理学报,2015,64(7):070503.

[13] 孙克辉,贺少波,董燕青.简化洛伦兹混沌系统的追踪同步控制[J].信息与控制,2015,44(4):393-397.

[14] THIAGARAJAN J J,RAMAMURTHY K N,SPANIAS A.Learning stable multilevel dictionaries for space representations[J].IEEE Transactions on Neural Networks & Learning Systems,2015,26(9):1913-1926.