2.25阶/2.5阶网络零模型模拟退火优化算法
2018-01-23宋玉蓉
吴 睿,宋玉蓉
(南京邮电大学 自动化学院,江苏 南京 210023)
1 概 述
通常,将具有与实际网络给定阶次度相关特性的随机网络称为该实际网络的随机化网络,这类随机化网络模型在统计学上称为零模型。Mahadeven等[1]为了从粗糙到精确逐步逼近真实网络的性质,按照约束条件从少到多,将零模型的阶次依次从低阶到高阶(0阶至3阶)进行了定义。不同阶数网络零模型之间并不是独立的,按照约束条件从少到多,存在一种包含关系,即任何一个d阶零模型都会包含d-1阶零模型的性质。通过原始网络(即实际网络)与不同阶次的零模型的比较,就可以检测到实际网络中一些性质的来源。
零模型生成方法有两种:网络模型方法和随机置乱方法。基于网络模型[2-4]生成零模型是一个从无到有生成新网络的过程,熟知的ER随机图[5]、WS小世界网络[6]、BA模型[7]、配置模型[8-9]等都可以视为网络模型方法。ER随机图可以视为阶数最低的0阶零模型(与原始网络具有相同的平均度),而配置模型可生成1阶(与原始网络具有相同的度分布)、2阶(与原始网络具有相同的联合度分布)或更高阶零模型。基于随机置乱生成零模型是将实际网络进行随机断边重连[10-11],在保持原有连接的前提下随机化某些因素。这种方法可以产生0至2.5阶网络零模型。Gjoka等[12]认为3阶网络零模型要求与原始网络具有相同的联合边度分布,其约束条件已经很多,不具备实用性;2.25阶零模型与原始网络具有相同的联合度分布和平均聚类系数;2.5阶零模型与原始网络具有相同的联合度分布和聚类谱,是现在能够实现的最高阶的实用零模型。
2.25阶和2.5阶零模型对研究网络的聚类特性有着重要作用。聚类特性作为一个重要的拓扑特性,对复杂网络上的动力学行为[13-15]影响显著。例如,有研究表明[2,16-17],高聚类网络可抑制病毒传播;Kim[18]等对神经网络的研究发现,网络的计算功能更多取决于聚类系数而不是度分布,且低聚类网络的性能优于高聚类网络。
网络中三角形的数量对聚类系数的变化有重要影响,通常三角形数量越多,聚类系数越大。文献[19]基于配置模型思想,根据固定的度序列与聚类谱,对一个只有节点的网络进行添边,生成指定度分布和聚类谱的网络模型。进行添边时主要依靠对三角形数量的控制。该算法无法控制同配系数,因此联合度分布会不同。
Bansal等[20]结合随机重连算法和马尔可夫链生成指定度分布和聚类系数的随机网络模型,简称ClustRNet算法。该算法从随机选择的节点入手,从该节点的邻居节点中随机选择两条边进行断边重连,确保有三角形生成,但也可能破坏现有三角形。该算法复杂度为O(M2),其中M为网络边数,该算法不能保证生成指定的联合度分布。
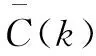
Gjoka等[12,22]评价文献[21]中的算法生成2.5阶零模型是不切实际的,虽然一开始会生成许多新三角形,但同时很可能破坏了更多已有三角形,此外因约束条件限制,导致该算法重复率很高,得到与原始网络相等的聚类谱的概率是很小的。为此,Gjoka等[12,22]对Mahadevan等[21]构造2.5阶零模型的随机重连算法进行了改进(MCMC改进算法):交换连边时更倾向于选择包含较少三角形的连边,在此理论基础上能够更少地破坏已有三角形,生成更多新三角形。为生成更多三角形,达到目标聚类谱,该文献对节点采样生成了联合度分布和度相关的聚类系数的有效估计量并成功构建了2阶零模型网络和2.5阶零模型网络。
在国内学者的研究中,文献[23-24]很好地总结了现有一些零模型构造算法及其应用。文献[25]针对生成的0阶、1阶、2阶网络零模型,提出了基于GPU的大尺度网络零模型分组生成并行算法。
为此,提出了一种生成2.25阶、2.5阶零模型的优化算法:dK-目标保持重连算法(d代表阶数,K代表度相关性)。该算法改进了Hamiltonian函数[26],并结合了模拟退火算法[27]和Metropolis准则。运用现有算法如dK-随机重连算法[21](d=0,1,2)生成所需2阶零模型,在2阶零模型基础上应用所提出的算法,生成与真实网络具有相同的联合度分布和聚类系数/聚类谱的2.25阶/2.5阶零模型。最后通过实验对该算法进行验证。
2 零模型生成算法及模拟退火算法
2.1 dK随机重连算法
静态无权网络中最常用的就是使用随机重连来产生复杂网络零模型。随机重连的方法主要是在原始网络的基础上将网络中原有的连边随机地断开重连,使原始网络模型尽可能随机化。由于随机重连算法简单、易操作,不需要理解和运用复杂的数学公式、也不会产生自环和重边现象,却能精确保持真实网络的一些物理属性,因此广泛应用于实际各种类型的网络分析中。
d=0:随机去除原始网络的一条边(i,j),再随机选择网络中两个不相连的节点a和b,并在它们之间添加一条连边(a,b)。
d=1:随机选择原始网络中的两条边(i,j)和(a,b),如果这四个节点之间只有这两条边,那么就去除这两条边,并将节点a和j相连、节点b和i相连,从而得到两条新边(b,i)和(a,j)。
d=2:随机选择原始网络中的两条边(i,j)和(a,b)并且ka=ki(节点a和i度值相同),如果这四个节点之间只有这两条边,那么就去除这两条边,并将节点a和j相连、节点b和i相连,从而得到两条新边(b,i)和(a,j)。
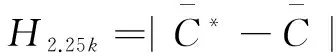
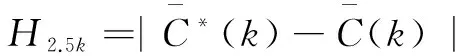
2.2 模拟退火算法
模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却。加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,在常温时达到基态,内能减为最小。
根据Metropolis准则:假设在状态xold时,系统受到某种干扰而使其状态变为xnew。与此相对应,系统的能量也从E(xold)变为E(xnew),系统由状态xold变成xnew的接受概率p表示为:
p=
(1)
粒子在温度T时趋于平衡的概率p为exp(-ΔE/kT),其中E为温度T时的能量,ΔE为其改变量,k为Boltzmann常数。用固体退火模拟组合优化问题,将改变量ΔE模拟为目标函数值ΔH,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法:由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解。这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。
退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值T0及其衰减因子Δt、每个t值时的迭代次数N和停止条件S。模拟退火算法是一种通用的优化算法,理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用,诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。
3 2.25阶、2.5阶零模型优化算法
为了用更少的迭代次数得到随机化更彻底的聚类网络(d=2.25,2.5),在使用dK-随机重连算法(d=0,1,2)的基础上结合模拟退火算法,提出了dK-目标保持重连算法(d=2.25,2.5)。
该算法具体步骤为:
Step1:设置初始参数。首先,从随机重连算法所述过程中得到的2阶零模型作为初始网络G0,并令其为目标优化网络。
设置优化目标误差值为He,系统初始温度T0,用于控制降温的快慢参数γ,同一温度内的网络未更新次数上限α,温度的下限Tmin。
Step2:计算G0与真实网络Gv关于聚类系数和聚类谱的Hamiltonian改进函数。
(1)关于聚类系数,即2.25阶:
(2)
(2)关于聚类谱,即2.5阶:
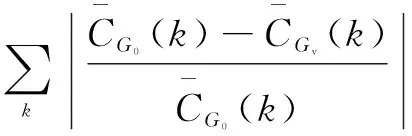
(3)
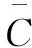
Step3:对G0网络执行随机断边重连算法,即从G0中随机选择两条边(u,v)和(x,y)且有ku=kx;变换连边,得到包含新边(u,y)和(x,v)的新网络Gn;
依据式(2)和式(3)计算Hn/Hkn。
Step4:令
ΔH=|Hn-H0|
(4)
或
ΔHk=|Hkn-Hk0|
(5)
计算网络更新概率:
(6)
或
(7)
以概率p/pk更新G0网络及相关参数,即令G0=Gn,H0=Hn或Hk0=Hkn。
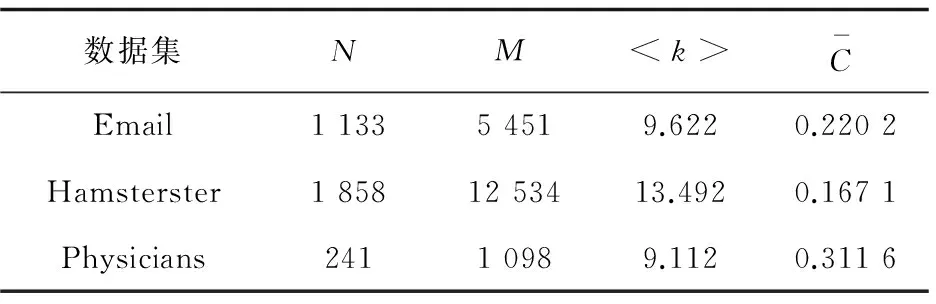
若H0 Step5:如果连续α次网络未获得更新,重复Step3和Step4,否则转到Step6。 Step6:降温过程: Tk=T0×γ (8) 若达到终止温度Tk Step7:输出G0,即为得到的2.25阶或2.5阶零模型网络。 实验选取三个无权无向的真实网络。其网络名称、数据规模、具体统计参数如表1所示。 表1 真实网络的具体统计参数 本算法需设置系统初始温度T0,用于控制降温的快慢参数γ,温度的下限Tmin,优化目标误差值He,同一温度内的网络未更新次数上限α。 系统初始要处于一个高温的状态,因此T0设为100。将He设为0.02,α设为8。 参数γ的设置很重要,若γ过大,则搜索到全局最优解的可能会较高,但搜索的过程也就较长;若γ过小,则搜索的过程会很快,但最终可能会达到一个局部最优值。对比分析了γ分别取0.85和0.95,终止温度Tmin分别取0.01和0.1时,生成2.25阶和2.5阶零模型时所需要的迭代次数。结果如表2所示,可以看到算法在取γ=0.95,Tmin=0.1时迭代次数最少,效果最好。 表2 算法参数设置对迭代次数的影响 运用dK-目标重连算法生成了2.25阶和2.5阶零模型后,统计出表3中每个真实网络生成的四个网络模型的平均聚类系数和聚类系数总和,以便于对算法误差率进行分析。 表3 三个真实网络及各阶零模型(d=2,2.25,2.5)聚类系数分析 接着,通过仿真分别对三个真实网络的聚类谱与2.25阶和2.5阶零模型网络的聚类谱进行了对比分析,以验证本算法生成的2.5阶零模型的有效性和准确性。仿真结果如图1所示。 图1 生成的2.25阶和2.5阶零模型与真实网络聚类谱的比较分析 从图1可以看出,三个真实网络的聚类谱分布均和本算法生成的对应网络的2.5阶零模型聚类谱分布几乎重叠,与2.25阶零模型聚类谱相差明显。仿真结果表明,本算法生成的2.5阶零模型具有较高的准确率和有效性。 将MCMC算法[21]、MCMC改进算法[12]和ClustRNet改进算法[20]以及文中提出的算法就算法复杂度进行对比。这些算法在生成2.25阶/2.5阶模型时都是建立在MCMC算法生成的同一2阶零模型的基础上进行迭代后获得。 特别说明,由于ClustRNet算法[20]不能保证生成指定的联合度分布,故对该算法进行一些必要的修改,将马尔可夫链中的度分布信息设置为联合度分布,以保证生成的2.25阶、2.5阶模型的联合度分布与真实网络相同。该算法重新命名为ClustRNet改进算法。 经过多次实验,使MCMC改进算法[12]和ClustRNet改进算法[20]与文中提出的算法得到的2.25阶、2.5阶零模型聚类系数与真实网络的目标误差He控制在0.02范围内。而MCMC算法在生成2.25阶时He为0.02,2.5阶时He为0.1。四种算法的迭代次数如图2所示。 图2 2.25/2.5阶零模型算法复杂度对比 从图中可以看出,提出的算法生成2.25阶和2.5阶零模型时在迭代次数上占有明显优势,有效降低了算法的复杂度。 为快速、有效地获得与真实网络具有相同的联合度分布和聚类系数、聚类谱的零模型,将模拟退火算法运用于构造2.25阶、2.5阶零模型,提出了一种目标保持优化策略。仿真结果表明,该算法生成的2.25阶、2.5阶零模型在具有准确性和有效性的同时,有效降低了计算复杂度,且其算法复杂度优于其他已有算法。 [1] MAHADEVAN P,HUBBLE C,KRIOUKOV D,et al.Orbis:rescaling degree correlations to generate annotated internet topologies[J].ACM SIGCOMM Computer Communication Review,2007,37(4):325-336. [2] NEWMAN M E.Properties of highly clustered networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2003,68(2):026121. [3] GUILLAUME J L,LATAPY M.Bipartite graphs as models of complex networks[J].Physica A Statistical Mechanics & Its Applications,2006,371(2):795-813. [4] SALA A,CAO L,WILSON C,et al.Measurement-calibrated graph models for social network experiments[C]//Proceedings of the 19th international conference on world wide web.[s.l.]:ACM,2010:861-870. [6] WATTS D J,STROGATZ S H.Collective dynamics of “small-world” networks[J].Nature,1998,393(6684):440-442. [8] MOLLOY M,REED B.A critical point for random graphs with a given degree sequence[J].Random Structures & Algorithms,1995,6(2-3):161-180. [9] NEWMAN M E,STROGATZ S H,WATTS D J. Random gr-aphs with arbitrary degree distributions and their applications[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2001,64:026118. [10] SERGEI M,KIM S.Specificity and stability in topology of protein networks[J].Science,2002,296(5569):910-913. [11] MASLOV S,SNEPPEN K,ZALIZNYAK A.Detection of topological patterns in complex networks:correlation profile of the internet[J].Physica A:Statistical Mechanics and Its Applications,2004,333:529-540. [12] GJOKA M,KURANT M,MARKOPOULOU A.2.5K-Graphs:from sampling to generation[C]//Proceedings of IEEE INFOCOM.[s.l.]:IEEE,2012:1968-1976. [13] PETERMANN T,RIOS P D L.The role of clustering and gridlike ordering in epidemic spreading[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2004,69(6):066166. [14] SOFFER S N,VZQUEZ A.Network clustering coefficient without degree-correlation biases[J].Physical Review E,2005,71(2):057101. [15] SERRANO M,BOGUM.Clustering in complex networks. I. General formalism[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2006,74(5):056114. [16] NEWMAN M E J.Random graphs with clustering[J].Physical Review Letters,2009,103:058701. [17] GLEESON J P,MELNIK S,HACKETT A.How clustering affects the bond percolation threshold in complex networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2010,81:066114. [19] ANGELES S M,BOGUM.Tuning clustering in random networks with arbitrary degree distributions[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2005,72:036133. [20] BANSAL S,KHANDELWAL S,MEYERS L A.Exploring biological network structure with clustered random networks[J].Bmc Bioinformatics,2009,10:405. [21] MAHADEVAN P,KRIOUKOV D,FALL K,et al.Systematic topology analysis and generation using degree correlations[J].ACM SIGCOMM Computer Communication Review,2006,36(4):135-146. [22] GJOKA M,TILLMAN B,MARKOPOULOU A.Construction of simple graphs with a target joint degree matrix and beyond[C]//IEEE conference on computer communications.[s.l.]:IEEE,2015. [23] 尚可可,许小可.基于置乱算法的复杂网络零模型构造及其应用[J].电子科技大学学报,2014,43(1):7-20. [24] 陈 泉,杨建梅,曾进群.零模型及其在复杂网络研究中的应用[J].复杂系统与复杂性科学,2013,10(1):8-17. [25] 李 欢,卢 罡,郭俊霞.基于GPU的大尺度网络零模型分组生成并行算法[J].计算机工程与设计,2016,37(1):93-99. [26] PARK J,NEWMAN M E J.Statistical mechanics of networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2004,70(2):066117. [27] GOFFE W L,FERRIER G D,ROGERS J.Global optimization of statistical functions with simulated annealing[J].Journal of Econometrics,1994,60(1-2):65-99.4 实验仿真
4.1 模拟退火算法参数分析

4.2 2.25/2.5阶零模型的有效性分析

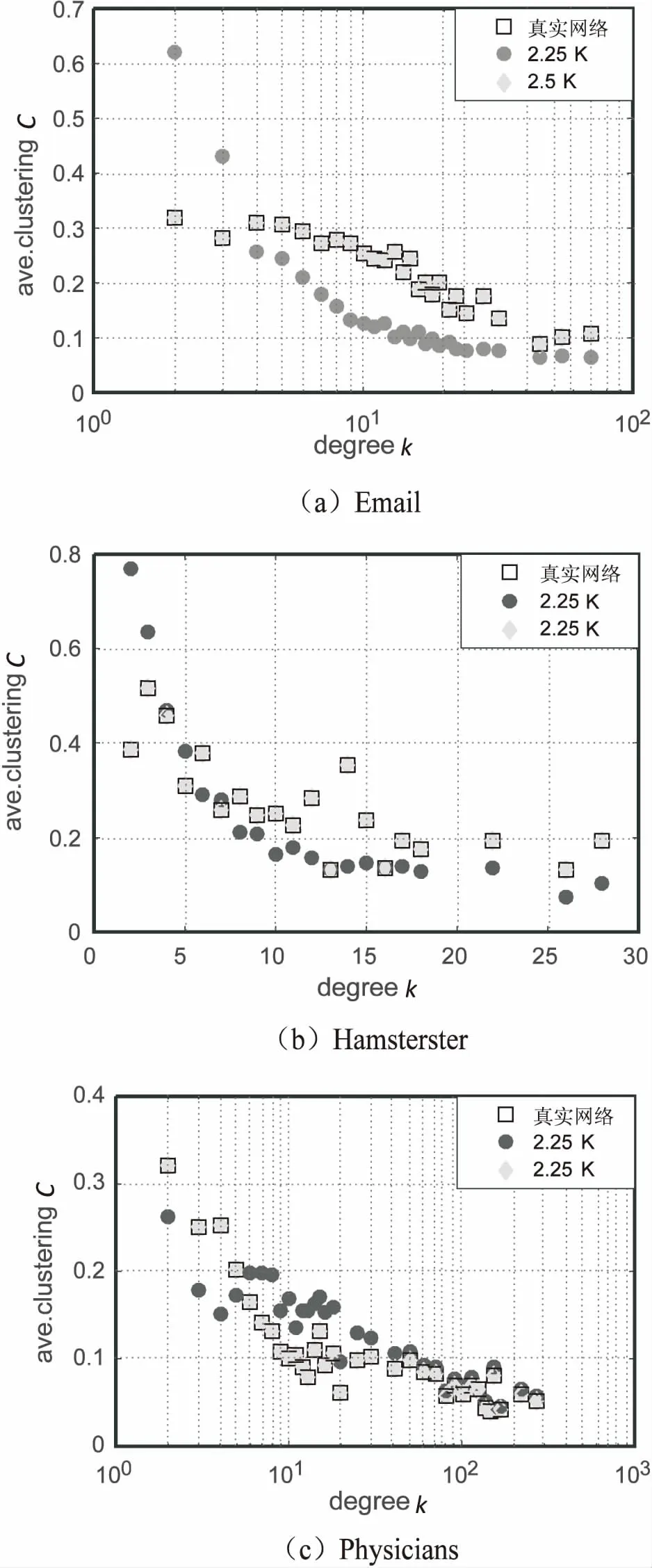
4.3 算法复杂度对比
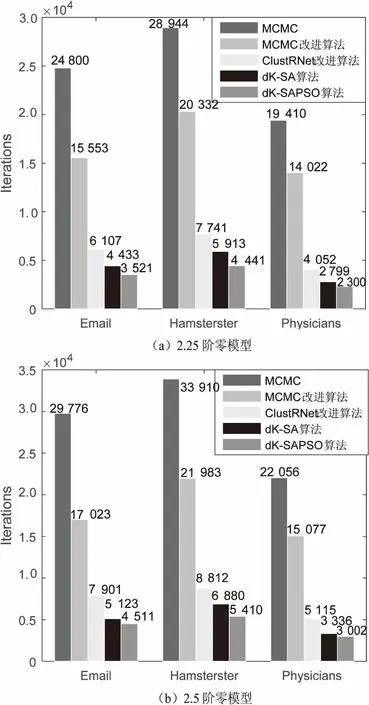
5 结束语
