基于聚类算法的购物篮压缩研究
2018-01-23张文斌褚维伟黄哲学
张文斌,明 勇,褚维伟,黄哲学
(深圳大学,广东 深圳 518000)
0 引 言
购物篮分析对零售业是非常重要的技术分析,尤其近年来网络零售的突飞猛进,产生了海量的交易数据,从而对购物篮分析提出了更高的要求。购物篮分析可以为超市和网络商城中的各种促销提供参考,去库存,商品布局优化。购物篮分析能为决策者提供快速、准确、节约、多元的信息参考。提高零售产业综合效益、提高国际竞争力、建设节约型社会购物篮分析都有重要的宏观意义[1]。
但是在传统的购物篮分析中,得出的结果通常是一些常规商品的组合。这些组合的购物篮支持度很高,但是它们已经被大家所认知,对企业的价值和意义不大。此外,传统购物篮分析一个很大的局限性在于它并不能预测,通常只对历史数据进行分析,而不是对购物篮按时间的序列做出演化和预测。往往精准的预测能给企业带来很大的利益,也能提高对风险的控制。还有,传统的购物篮分析只给出比较简单的结果,没有实现数据可视化。一幅图胜过千言万语,人类对外界过多的信息约有80%以上来自于视觉系统,当大数据以直观可视化的图形形式展示在分析者面前时,分析者往往能够一眼洞悉数据背后隐藏的信息并转化为知识以及智慧。购物篮可视化结果实现友好人机交互界面就需要研究数据可视化,同时,大数据本身的新特点也对可视化提出了更为迫切的需求。
针对购物篮分析的现状,结合企业实际应用中的需求,在购物篮压缩研究分析的基础上,设计并建立了购物篮可视化系统。其中,通过购物篮压缩来压缩并筛选更有价值的购物篮,购物篮可视化让购物篮分析结果实现友好的人机交互界面及可视化[2]。
1 购物篮重组分析
通常说的购物篮分析指的是通过购物篮中显示出来的交易信息来分析顾客的购买行为,顾客在购买商品的过程中通常会一次购买多个商品,从而使得这些商品之间具有很强的关联性。因此,可以认为顾客的购买行为是一种整体的行为,是否购买一件商品会影响到其他商品的购买,从而影响到每个购物篮的利润。所以,购物篮分析的目标就是找出重要且有价值的购物篮[3]。
关联规则挖掘是购物篮数据挖掘最经典的应用之一,用来从大量的数据中挖掘出一些令人感兴趣的规则,分析产品之间的关联性,从而指导人们做出一些有利的决策和安排。例如在超市中将啤酒和尿布放在一起会增加啤酒的销量等。
关联规则挖掘问题最早是在1993年由AGRAWAL等提出的,主要是为了帮助零售企业分析交易数据,对一些商业决策提供支持,如怎样制定促销方案,怎样摆放商品来提升销售业绩,怎样决定供货数量来减少库存,等等。他们认为,关联规则挖掘问题主要通过两部分来解决,即先挖掘出大项集集合,再从大项集集合中挖掘出关联规则。同时提出了语法约束和支持度约束的概念,并且提出了AIS算法来生成大项集集合[4]。
关联规则挖掘问题可以表述为:设I=[i1,i2,…,in]是所有项目的集合,即所有商品类别的集合;D=[T1,T2,…,Tn]是所有事务的集合,即所有交易记录的集合。事务T可以表示为:T=[TID,
2 购物篮聚类分析
2.1 购物篮聚类的意义
购物篮分析在实际场景中应用时往往得出的是数以千计的购物篮,企业很难从这数量繁多的购物篮中找出真正感兴趣的、对自己有价值的部分。购物篮分析中最经典的案例莫过于“啤酒和尿布”了,可是这之后就很少有类似的购物篮分析结果了。购物篮数量的问题给购物篮分析的应用造成了很大的阻碍。为了解决这个问题,自然而然就会想到去压缩这些数量庞大的购物篮,例如,用一种简洁的表达来描述一类购物篮。对购物篮通过聚类进行压缩,再从聚类结果中找出代表性的购物篮,从而大大减少购物篮数量[5]。
2.2 购物篮聚类算法
K-Means算法是基于划分的聚类算法,简洁易懂且有较高的效率,因此应用十分广泛。用户给定一个期望得到的聚类数k,K-Means算法就可以通过某种距离函数反复地把数据集中的点分到这k个类中,直到满足某个终止条件。
设数据点的集合为X=[x1,x2,…,xn],其中xi=[xi1,xi2,…,xir]为r维向量,K-Means算法将把给定的数据集划分成r类,每个类有一个聚类中心。聚类中心为这个类中所有点的均值,通常用聚类中心来表示这个类。K-Means聚类算法描述如下:
输入:数据集D,聚类个数k
输出:k个类
步骤:
选择k个数据点作为原始聚类中心
repeat
for each data pointx⊂Ddo
compute the distance fromxto each centroid
计算x到每个聚类中心点的距离
assignxto the closest centroid //将x分配到距离最近的类中
endfor
re-compute the centroid //重新计算每个类中的聚类中心点
until the stopping criterion is met
首先从数据集中随机抽取k个点作为原始聚类中心,然后计算每个数据点到这k个聚类中心的距离,并根据这个距离值将每个数据点分到最近的聚类中心,当分配完所有的数据点之后,重新计算每个类中的聚类中心。不断重复这一过程直到满足某个终止条件。终止条件为以下三个中的任何一个:
(1)没有(或最小数目)数据点被重新分配给不同的类;
(2)没有(或最小数目)聚类中心发生变化;
(3)误差平方和局部最小。
(1)
均值为使得簇的误差平方和最小的质心,即:
(2)
其中,k为用户设定的聚类簇个数;x为对象;Ci为第i个簇;ci为第i个簇的质心;dist(x,ci)为数据点x到簇中心ci的距离;mi为第i个簇中包含的数据点个数。
证明过程如下:
对于一维数据,式(1)可以写成:
(3)
其中,Ci表示第i个簇;x表示Ci中的点;ci表示簇Ci的均值。
然后求解第k个质心ck,最小化式(3),也就是对SSE求偏导数,令偏导数为0,再求解ck。
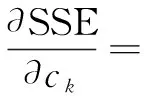
(4)
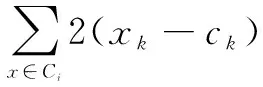
(5)
因此,簇中各点的均值是簇的最小化误差平方和的最优质心。
K-Means算法虽然简洁易懂、效率较高,但是实际应用中也有很多不足之处。这里运用K-Means算法进行购物篮聚类存在的问题主要为用户需要指定聚类数目k,这个k值的选定是非常难以估计的。很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适。若k值设置过大,会导致聚类数目过多,达不到压缩购物篮集合的目的;若k值设置过小,会导致聚类结果过于粗糙,不够准确[6-7]。
3 购物篮压缩方法
购物篮集合压缩方法与代表模式方法类似,也是通过聚类实现的。不同的是,聚类的对象不再是购物篮表达式本身,而是由一系列特征属性表示的购物篮[8]。
3.1 数据预处理及属性构造
在数据挖掘的整体过程中,海量的原始数据中存在着大量杂乱的、重复的、不完整的数据,严重影响了数据挖掘算法的执行效率,甚至可能导致挖掘结果的偏差[9]。为此,在数据挖掘算法执行之前,必须对收集的原始数据进行预处理,以改进数据的质量,提高数据挖掘过程的效率、精度和性能。数据预处理主要包括数据清理、数据集成、数据交换与数据归约等[10]。
数据预处理可以补全残缺的数据,纠正错误的数据,删除多余的数据,筛选出所需的数据并进行数据的集成操作,转化数据为需要的格式,从而实现数据类型的相同化、数据格式的一致化、数据信息的精练化以及数据存储的集中化[11]。通过数据预处理后,可以得到数据挖掘所需要的数据集,从而使数据挖掘具有可行性;同时也可以在一定程度上减少进行挖掘所需付出的代价,提高挖掘结果的可理解性与有效性[12]。
为了对上面得出的购物篮进行聚类以达到压缩购物篮集合的目的,首先对购物篮进行属性构造。通过对交易数据的仔细分析与深入理解,首先对每个购物篮构造了13个属性。
另一方面,有的购物篮具有较强的时间特征,会受到季节、节假日等时间因素的影响。基于此,将用于产生购物篮的原始交易数据按月分割,计算每个购物篮在每个月中这13个属性的值。这样得到的购物篮属性就形成了一个12个月的时间序列,其中每个月都有13个属性,最后每个购物篮共有156个属性。在构造完这些属性之后,发现像支持度和销售额占比这些属性值都非常小。而在聚类的过程中,如果属性值太小,在计算距离时权重就很小,近似为0,对聚类结果影响较大。因此,在聚类之前还要进行属性值的正规化操作,将所有属性值都映射到[0,1]区间[13]。
3.2 购物篮压缩算法
针对K-Means算法应用在购物篮集合压缩中的不足之处,结合基于划分和基于层次的聚类方法,提出一种基于K-Means的层次聚类算法。算法详细描述如下:
(1)将原始数据集D用K-Means()算法分裂成k个子聚类;
(2)分别对上一次聚类产生的所有子聚类运行K-Means()算法;
(3)重复第2步,直到满足终止条件。
算法的主要思想是自上而下的分裂聚类。聚类过程从整个数据集的聚类(根)开始,根据用户指定的k值,运用K-Means算法将根节点聚类分裂成k个子聚类。每个子聚类再递归地继续往下分裂直到满足某个终止条件。终止条件为以下任何一个:
(1)所有的叶节点中数据点的个数都小于k;
(2)没有叶子节点再分裂成子聚类。
图1为聚类结果示例,聚类结果为一棵聚类树。树的叶子节点有5个聚类(5个数据点),在上一层中,聚类4包含叶子节点5和6,聚类3包含叶子节点8和9。用到的结果只需要最底层的叶子节点的聚类信息,即5和6为一个聚类,7为一个聚类,8和9为一个聚类[14]。
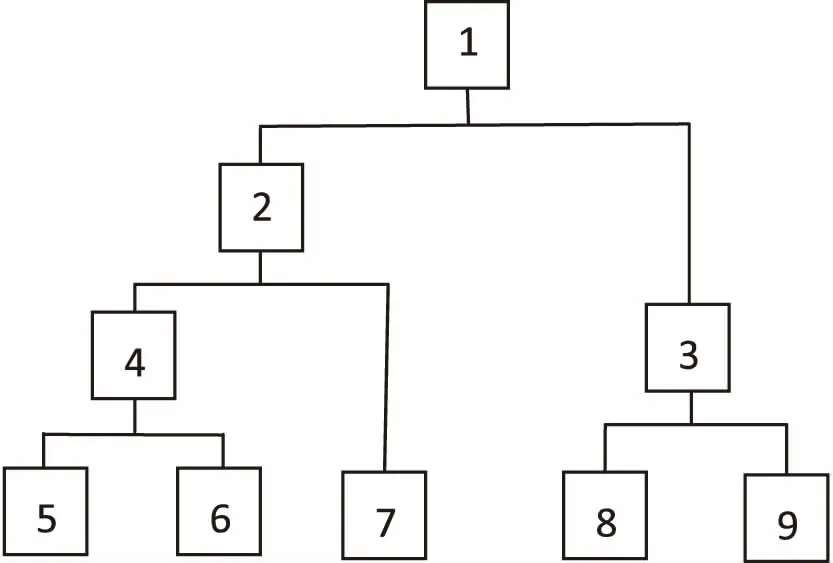
图1 聚类结果示例
通过上文所述的聚类方法,将购物篮集合划分成n个聚类。接下来从每个聚类中找出一个购物篮来表示这个聚类中的所有购物篮,这样就将原始的购物篮集合压缩成n个购物篮。在每个聚类中,根据购物篮中商品出现的频次来构造代表购物篮。
4 实验结果分析
为了检验购物篮聚类方法在实际应用中的效果,采用购物篮集合作为输入数据对效果和性能进行验证。输入数据为500个购物篮,并按3.1的方法进行了数据预处理和属性构造,这样每个购物篮为一个聚类对象,有156个特征属性。通过文中提出的购物篮聚类方法,将500个购物篮划分成了50个类,在每个类中找出一个代表购物篮,从而实现了购物篮压缩。下面首先对聚类效果进行评估与分析。
图2为聚类结果中每个聚类中的点到聚类中心的距离分布图,用来评估聚类结果中的类内是否紧密。
从图中可以看出,聚类中点到聚类中心的距离主要集中分布在0.05到0.2之间,其中距离在0.1至0.15之间点的占比达到50%以上。图1表明聚类结果中每个聚类比较紧凑,聚类效果较好,达到了使相同类中样本尽可能相似的目的。
采用雷达图的形式来对比购物篮聚类前后的差别。图3为购物篮聚类之前的购物篮数据雷达图,这里考虑到购物篮在不同月份的表现具有较大差异,将购物篮属性按月划分,由每个月的购物篮数据得到一张雷达图。其中每个月份的雷达图有13个顶点,代表3.1中构造的13个基本属性,通过观察每个雷达图的形状就可以判断购物篮的分布情况。如果雷达图中购物篮的轨迹比较杂乱、分散,则说明购物篮集合差异性较大。反之,如果雷达图中购物篮形成的轨迹具有明显的相似性,则说明这些购物篮具有很强的共性。由图3可以看出,购物篮聚类前较为分散,没有什么规律性。
图4为聚类结果中聚类中心点间距离分布直方图,用来评估聚类结果中类间是否远离。由图中可以看出,聚类中心点间的距离主要分布在0.2至0.4之间,占比达到60%以上。而由图2可知,每个聚类中点到聚类中心的距离主要分布在0.05到0.2之间,对比实验结果可表明聚类结果中不同类间较为分散。
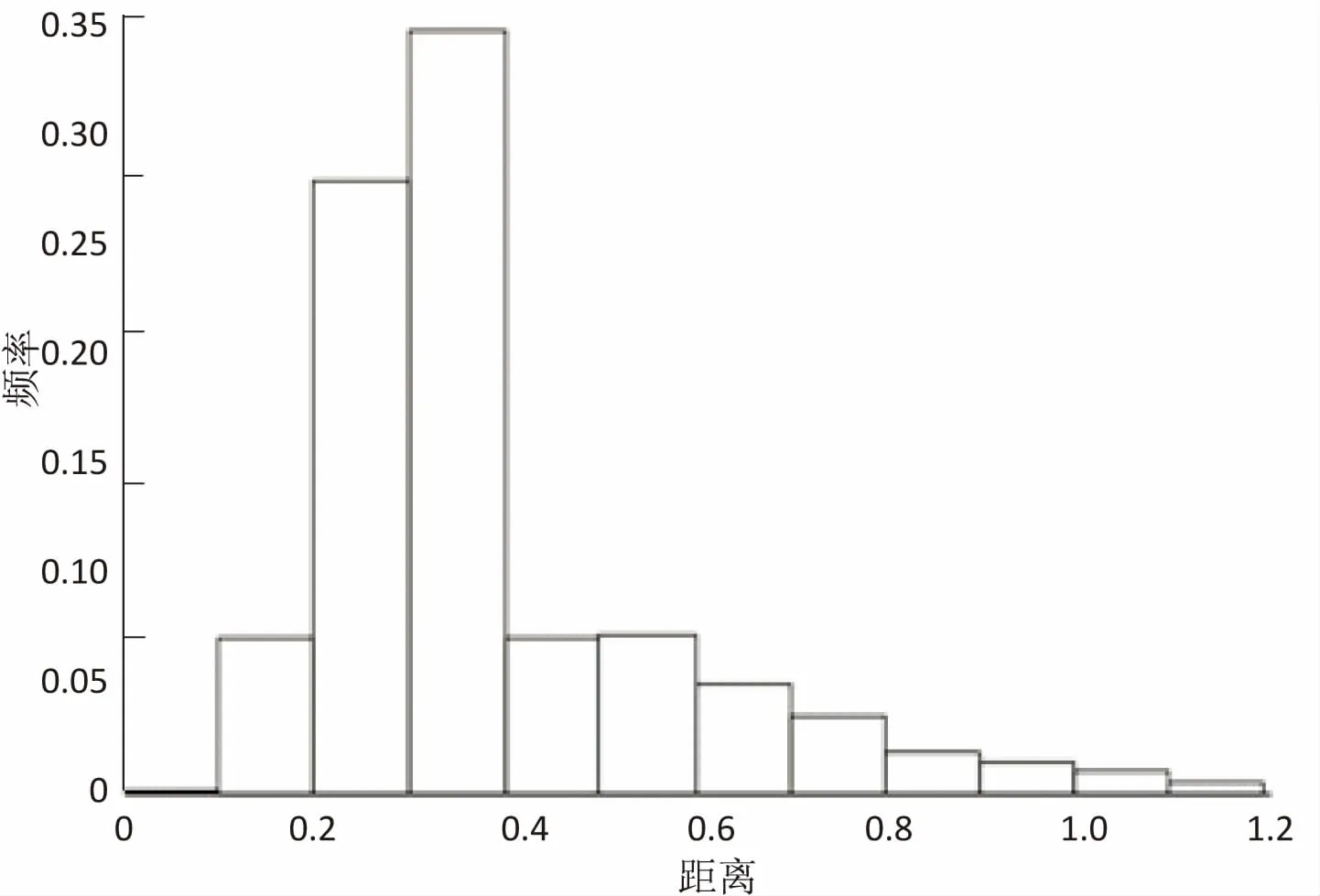
图4 聚类中心点间距离分布直方图
由以上两个实验,可以得出所提出的购物篮聚类算法满足类内紧密、类间远离的聚类有效性评估标准,有较好的聚类效果。
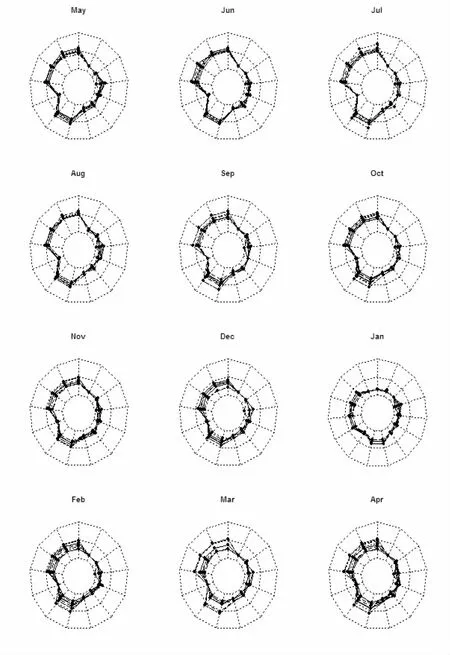
(a)聚类1的购物篮数据雷达图

(b)聚类2的购物篮数据雷达图
在实验得到的50个聚类中,选择两个作为购物篮聚类结果示例。由图5可以看出,每个聚类中的12张雷达图形状非常相似,每张雷达图中的购物篮轨迹也基本重叠,有明显的相似性。通过对比可以看出,聚类后同一个类中的购物篮具有较高的相似度,说明提出的购物篮聚类方法具有较好的聚类效果。
下面对从聚类结果中选择代表购物篮进行评估与分析,以代表购物篮中的商品在类中出现的频次占比作为评估代表购物篮的标准,显然占比越高则说明选择的购物篮越有代表性。图6为代表购物篮中商品在类中出现的频次占比分布直方图。
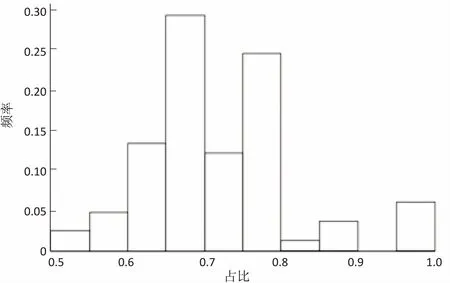
图6 代表购物篮中商品在类中出现的频次占比
由图6可以看出,这一占比值普遍较高,都在50%以上,主要分布在60%至80%之间,表明所采用方法具有较高的有效性与实用价值。
根据算法描述以及实验结果,可以总结出文中提出的购物篮压缩方法具有以下优点:
(1)结合基于划分和基于层次的聚类方法,提出基于K-Means的层次聚类算法。算法简单高效,不用人工输入k值,避免了因k值设置不当导致的聚类效果不理想。
(2)根据聚类中商品出现的频次来构造代表购物篮,保留了聚类中影响最大的商品,具有较高的代表性与有效性。
5 结束语
购物篮数量过多是购物篮分析在实际应用中不可避免的问题,而传统的压缩方法中关注的对象都是购物篮表达式本身,效果并不是很理想。文中提出的购物篮压缩方法为每个购物篮构造了具有时间序列特征的属性,然后根据这些属性值对购物篮进行聚类,再从聚类结果中挑选出代表购物篮,从而达到了压缩购物篮集合的效果。
[1] 余 颖.购物篮分析在网络零售业中的应用研究[D].天津:天津大学,2007.
[2] 褚维伟,张文斌,陈小军,等.一种带约束条件的购物篮分析方法[J].计算机技术与发展,2016,26(8):69-74.
[3] DIPPOLD K,HRUSCHKA H.Variable selection for market basket analysis[J].Computational Statistics,2013,28(2):519-539.
[4] 黄 鹤.关联规则算法综述[J].软件导刊,2009,8(3):56-57.
[5] 罗 芳.基于聚类和压缩矩阵的加权关联规则算法的研究与应用[D].上海:华东师范大学,2010.
[6] 高 滢,刘大有,齐 红,等.一种半监督K均值多关系数据聚类算法[J].软件学报,2008,19(11):2814-2821.
[7] RUPALI S,SHAH T,CHAVAN T,et al.Survey on implementation of market basket analysis using Hadoop framework[J].International Journal of Computer Applications,2016,134(10):6-9.
[8] SOLNET D,BOZTUG Y, DOLNICAR S. An untapped gold mine? Exploring the potential of market basket analysis to grow hotel revenue[J].International Journal of Hospitality Management,2016,56:119-125.
[9] 张平庸,欧阳为民,万志华.基于密度的购物篮数据聚类方法[J].计算机工程与设计,2005,26(1):180-181.
[10] CHEN Y L,TANG K,SHEN R J,et al.Market basket analysis in a multiple store environment[J].Decision Support Systems,2005,40(2):339-354.
[12] KOCSOR A,KERTÉSZ-FARKAS A,KAJN L,et al.Application of compression-based distance measures to protein sequence classification:a methodological study[J].Bioinformatics,2006,22(4):407-412.
[13] 李雷定,马铁华,尤文斌.常用数据无损压缩算法分析[J].电子设计工程,2009,17(1):49-50.
[14] 彭喜元,俞 洋.基于变游程编码的测试数据压缩算法[J].电子学报,2007,35(2):197-201.
