基于递推最小二乘法惯量辨识的伺服控制算法*
2018-01-22张静
张 静
上海电气集团股份有限公司 中央研究院 上海 200070
1 课题背景
外部负载环境的变化主要体现在负载转动惯量的变化上,而负载环境对于电流环等内环的影响并不明显,因此,高性能的伺服系统需要适应负载惯量的变化,并及时调整对应参数来保持或提高系统的控制性能。原始的做法是通过附加设备对系统惯量进行识别,但过程复杂,成本高。目前比较流行的方法有离线辨识和在线辨识[1-5]。
离线辨识算法大多需要给定特殊的指令信号,如在位置环的指令信号中注入高频、低幅值正弦波,并提取高频下的电磁转矩和机械角度信号,利用运动方程,获取转动惯量[6]。不足之处在于,系统位置信号可能会不允许叠加正弦谐波,且频率提取模块要消耗内存,难以实现在线辨识。
在线辨识算法基于现代控制理论,根据已有的系统输入量和输出量,以及两者的数学关系式,来推导计算出中间量,应用到惯量辨识中,即为伺服电机的等效负载惯量[7-8]。
2 伺服控制系统数学模型
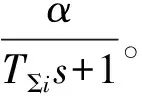
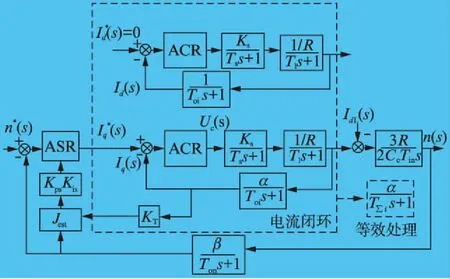
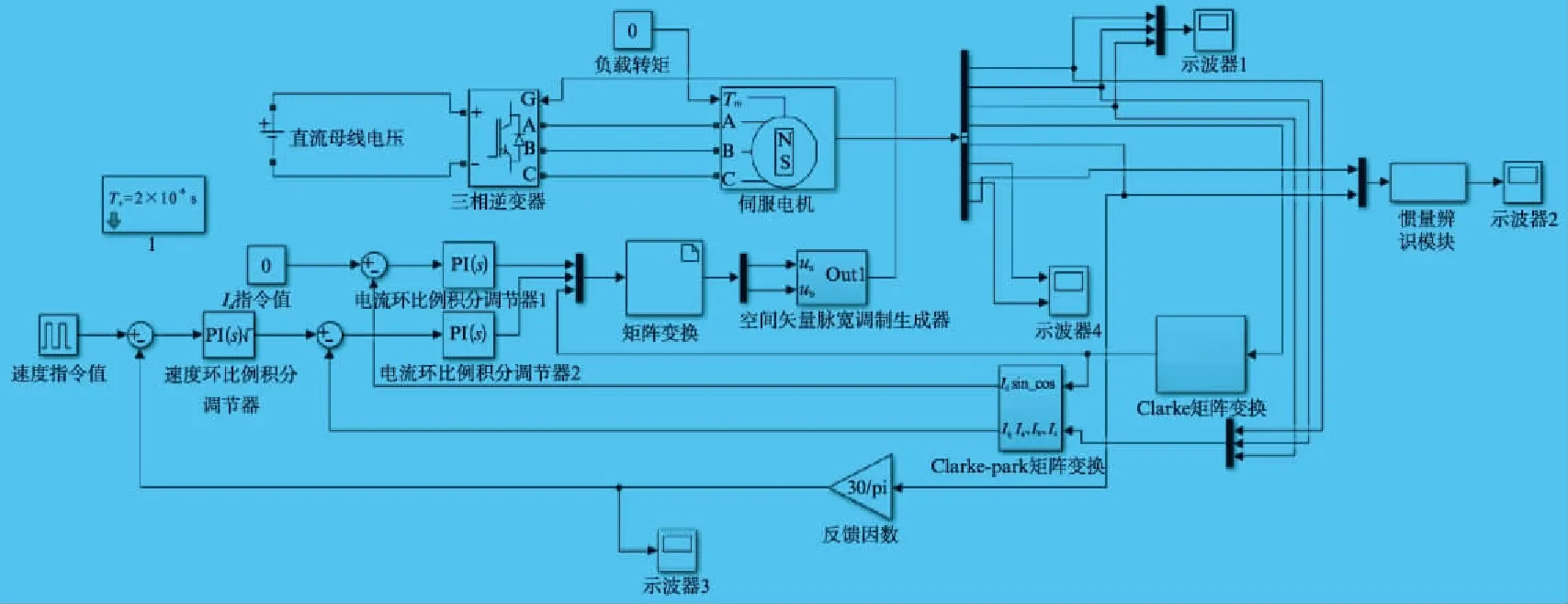
图1 伺服控制算法框架图
图1中符号意义如下:Tl为电磁时间常数,Ks为逆变器放大因数,Toi为电流环滤波时间常数,Ton为速度环滤波时间常数,Ts为离散时间,KT为标幺化后的转矩因数,IdL(s)为扰动负载的等效电流,Id*(s)、Iq*(s)分别为直交轴电流的给定,Id(s)、Iq(s) 分别为直交轴电流的反馈,n*(s)、n(s)分别为转速指令与反馈转速,ACR为电流环控制器,ASR为速度环控制器,Kps、Kis分别为速度环控制器中的比例和积分因数,Kps=kn,Kis=τn,α、β分别为电流环与速度环的反馈因数,Jest为等效负载转动惯量。
机电时间常数Tm与伺服电机物理参数的关系为:
(1)
式中:J为转动惯量;R为伺服电机电阻;Ce为反电势因数;Cm为转矩因数,Cm=30Ce/π。
现设KN为速度环的开环增益,推导得:
(2)
3 基于递推最小二乘法(RLS)的惯量辨识
等效负载惯量辨识是比例积分参数自整定的基础。笔者采用在伺服驱动器领域中比较成熟的惯量辨识技术算法,即RLS。此算法的优点是对指令几乎无要求,可实现实时辨识[12]。
3.1 RLS原理
RLS计算过程简单,可节省数字信号处理器内存,同时能在白噪声的系统中进行无偏参数估计。其原理可由离散单输入单输出系统进行说明。典型的离散单输入单输出系统框图如图2所示,图中x(k)为输入量,y(k)为输出量,e(k)为偏差量,H(z)为系统函数。
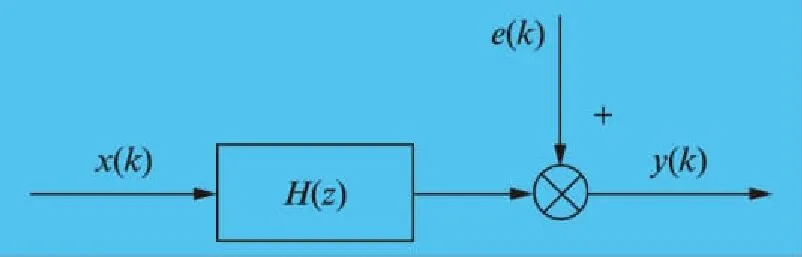
图2 离散单输入单输出系统框图
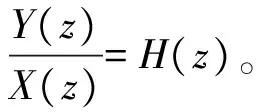
(3)
式中:n≤m;z=esT,T为采样周期。
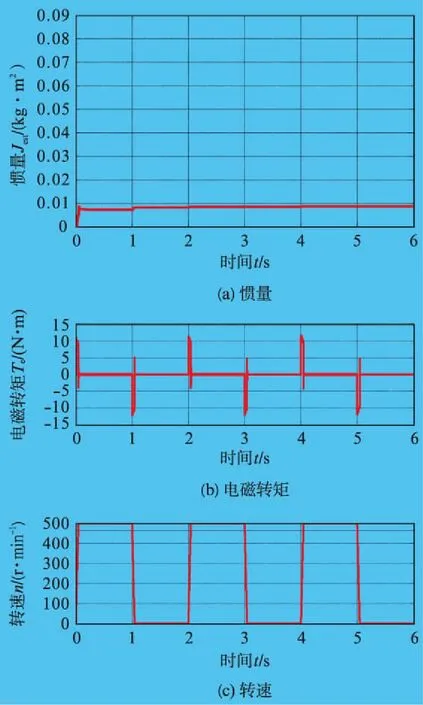
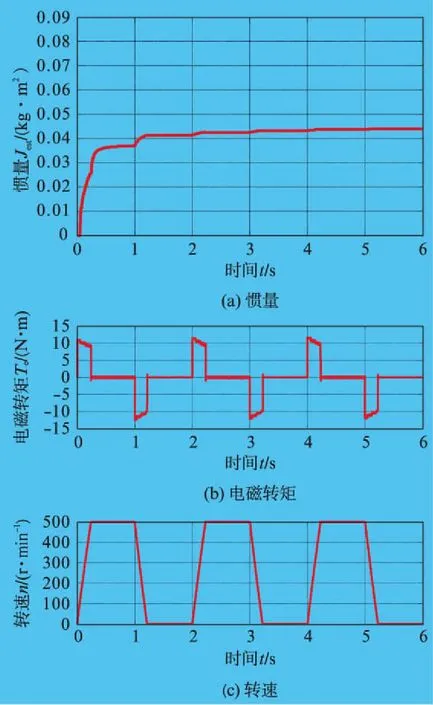
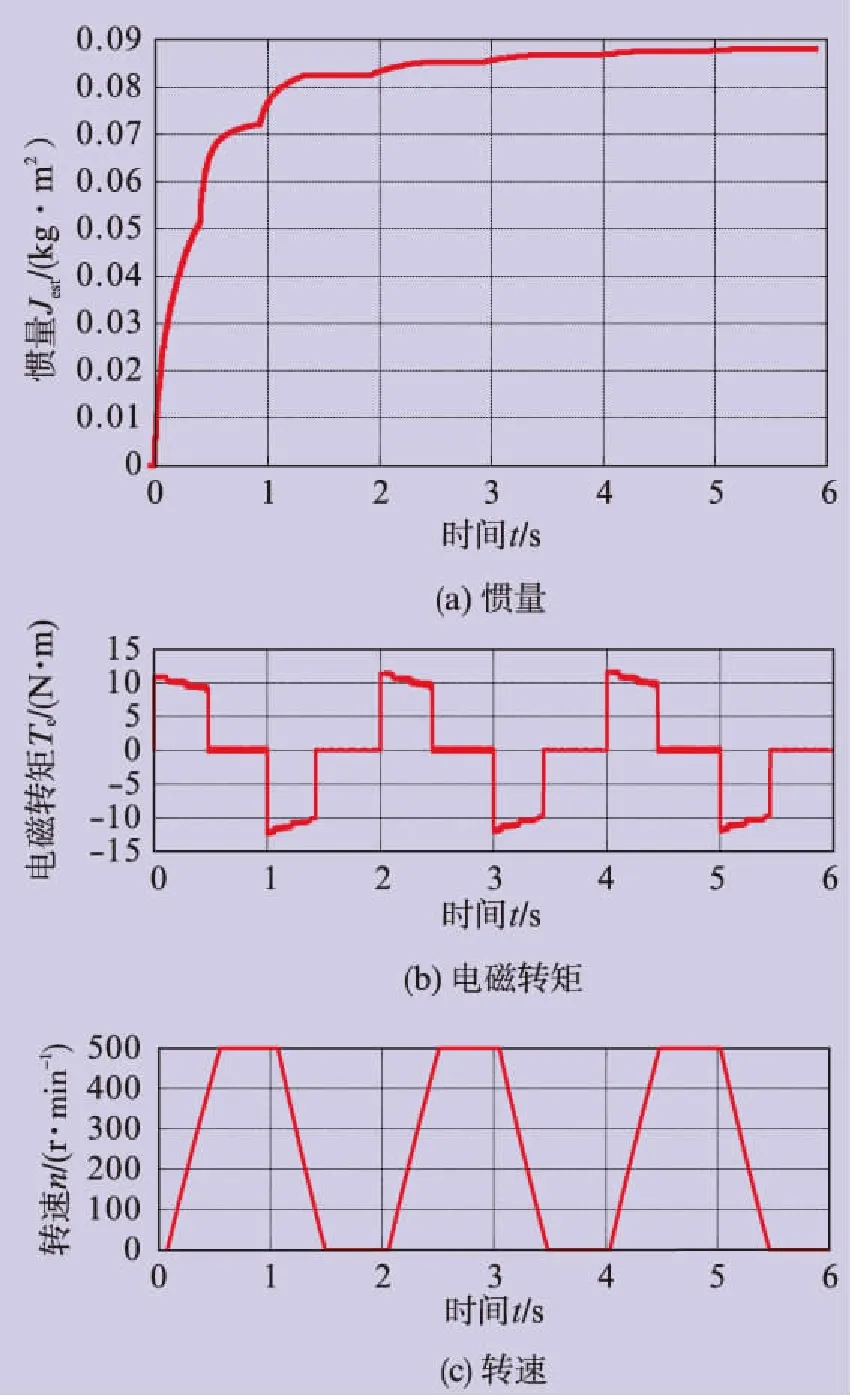
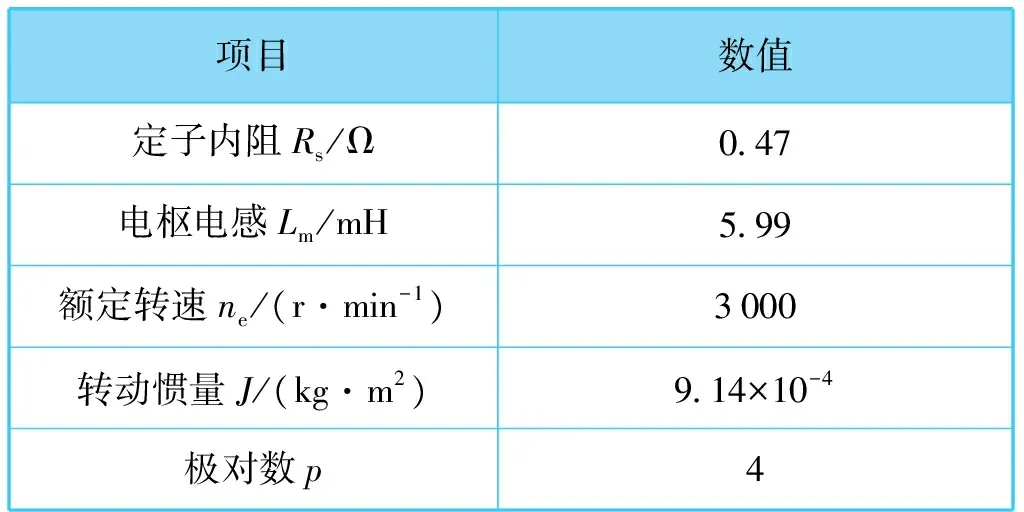
n代表输出量的采样次数,b1,b2,…bn代表输出量在此次采样时刻的因数,m代表输入量的采样次数,a1,a2,…am代表输入量在此次采样时刻的因数。n 将式(3)写成如下时域差分方程形式: (4) 式中:ai、bi分别为i时刻采样得到的输入量与输出量因数。 在实际系统中,模拟电路的精度不足、系统模型误差及噪声干扰等均可归为RLS理论中的误差e(k)。对于n阶差分方程,需要前n个时刻的输入输出量,则式(4)可整理成如下形式: (5) 在实际伺服控制系统中,伺服电机运动方程可用下式表示: (6) 式中:B为黏滞摩擦系数;Te为电磁转矩;TL为负载转矩;ωm为转子机械速度。 由于实际数字信号处理器中的转速信号为离散数据,因此需在式(6)中加入采样时间为T的零阶保持器,从而得到离散化后的运动方程式: (7) 式中:Kt为转矩因数;Δiq(z)为被测伺服电机中交轴电流与负载伺服电机中交轴电流的偏差。 (8) 将式(8)代入式(7),得到式(9)和(10): (9) (10) 将式(9)写成矩阵形式,得: ωm[k]=(Δiq[k-1],ωm[k-1])(θ1,θ2)T (11) 式中:θk为第k次中间变量矩阵,θk=(θ1,θ2)T;ωm[k] 为第k次转子机械速度;Δiq[k-1]为第k-1次两类交轴电流的偏差;k为迭代次数。 由式(10)可知,只要辨识出θ1和θ2,就可得到Jest。根据RLS的递推估计式,可得: (12) 式中:I为单位矩阵;Pk为第k次协方差矩阵;Kk为增益矩阵。 结合式(10)和(12),可实现基于RLS的等效负载惯量辨识,一般选取如式(13)所示的初始值θ0和P0: (13) a为一个数值,由于106≫0,即106相对于0已足够大,因此此处取a=103。 根据RLS公式辨识中间变量θ1和θ2,得出Jest。搭建基于RLS的惯量辨识仿真平台来验证此算法,如图3所示。 仿真中,伺服电机参数见表1。 表1 伺服电机参数 给定速度为500r/min、频率为0.5Hz、占空比为50%的方波信号。在仿真过程中,使Jest为10J、50J和100J,辨识结果如图4~图6所示。 等效负载惯量辨识基于伺服电机运动方程,采集转矩和电角度信号作为输入信号,再通过计算中间变量,估算出实际的等效负载惯量值。 仿真结果表明,基于RLS的辨识结果与真实值较为贴近。同时,从转速时间曲线图中可以看出,在不改变比例积分参数的情况下,随着等效负载惯量的增大,伺服系统的速度动态响应会变慢。为此,随着等效负载惯量的改变,速度环比例积分参数需进行相应调节,以获取最优的速度响应。 笔者从理论上分析了等效负载惯量变化时,速度环参数需要进行相应调整的原因。同时,等效负载惯量辨识是速度环比例积分参数自整定的基础和前提。为此,采用了基于RLS的惯量辨识策略,建立了离散化的伺服电机运动方程,并结合RLS原理推导出等效负载惯量辨识公式。此公式适用于伺服控制系统中等效负载惯量的辨识,具有一定的适用性。通过在计算机软件中搭建伺服控制系统的仿真平台,验证了基于RLS的等效负载惯量辨识的准确性,同时也验证了随着负载惯量的增大,若速度环比例积分参数不调整,则会带来速度响应变慢的问题。 图3 基于RLS的惯量辨识仿真图 图4 10J下辨识结果 图5 50J下辨识结果 [1] 梁骄雁,胡育文,鲁文其.基于梯度算法的永磁伺服系统惯量辨识性能研究[J].航空学报,2011,32(3): 488-496. 图6 100J下辨识结果 [2] 卢少武,唐小琦,宋宝.伺服系统转动惯量辨识及其应用[J].微电机,2011,44(10): 41-43,88. [3] 杜帅.永磁同步电机转动惯量辨识研究[J].电机与控制应用,2012,39(4): 17-22. [4] 丁信忠,张承瑞,李虎修,等.永磁同步电机的转动惯量辨识及状态估计[J].山东大学学报(工学版),2012,42(2): 70-76,82. [5] 王璨,杨明,栾添瑞,等.双惯量弹性伺服系统外部机械参数辨识综述[J].中国电机工程学报,2016,36(3): 804-817. [6] 牛里.基于参数辨识的高性能永磁同步电机控制策略研究[D].哈尔滨:哈尔滨工业大学,2015. [7] 刘子剑.伺服系统在线参数自整定及优化技术研究[D].哈尔滨:哈尔滨工业大学,2014. [8] 许林.交流伺服系统转动惯量辨识策略研究[D].武汉:华中科技大学,2008. [9] 鲁文其.永磁同步电机工程伺服系统若干关键技术研究[D].南京:南京航空航天大学,2010. [10] 周春,欧阳丽,古云蛟,等.NPC三电平光伏逆变器并网控制策略仿真研究[J].上海电气技术,2015,8(2): 41-47. [11] 杨明,刘子剑,徐殿国.基于遗忘因子递推平方根的在线转动惯量辨识[J].微电机,2014,47(10): 38-41,46. [12] 林尧.高压变频技术发展现状及趋势[J].装备机械,2013(2): 70-74.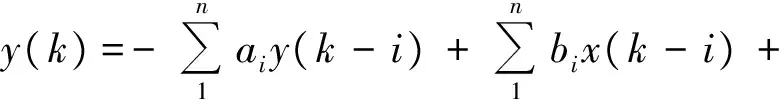
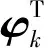
3.2 惯量辨识
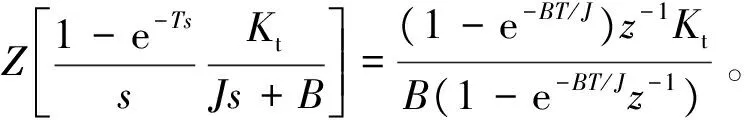
4 仿真验证
5 结论