Braneworld Black Hole Gravitational Lensing∗
2018-01-22JunLiang梁钧
Jun Liang(梁钧)
College of Arts and Sciences,Shannxi University of Science and Technology,Xi’an 710021,China
1 Introduction
The study of the black holes as gravitational lenses has received great attention in the last few years,mainly due to the evidence of the presence of a super-massive black hole at the center of our galaxy.[1]Gravitational lensing by an ordinary star or galaxy can be analyzed in the weak field approximation.[2]This approximation is only valid for photons with large impact parameter(see Fig.1).While for gravitational lensing by a black hole,a full strong field treatment is needed,which is because large de flection angles are possible for photons passing close to the photon sphere(see below for detail about the photon sphere).These photons could even perform one or more complete loops,in both directions of rotation,around the black hole before ultimately reaching an observer.As a consequence,besides the primary and secondary weak field images(formed by photons performing no loops),a theoretically in finite number of images(called relativistic images)are produced on either side of lens,corresponding to successive winding numbers around the black hole(see Fig.2).In 2002,Bozza[3]developed an approximate analytical method called the strong de flection limit for obtaining the de flection angle for a general class of static,spherically symmetric black hole.(Before Bozza’s paper was published,some works studying strong field lensing scenarios had been done. See,for example,Refs.[4–11].) He applied this method to Schwarzschild,R-N and Janis–Newman–Winicour black holes.Subsequently,many works of gravitational lensing by using Bozza’s method have been done for different types of static spherically symmetric black holes and rotating black holes.[12−44]In addition,Bozza’s method can also be used to calculate time delays between relativistic images.[45−47]
On the other hand,in recent years,brane world received a considerable attention from the physical community by reason of the hierarchy problem.[48]In brane world scenario,our world is a 4-dimensional submanifold(called “brane”)embedded in a higher-dimensional spacetime(called “bulk”),and the Standard Model particles are assumed to live on the brane,whereas the gravitational field is free to propagate in the bulk.[49]Gravitational collapse of matter on a brane will produce a black hole on the brane.[48]Static and spherically symmetric brane world black hole solutions can be obtained by solving the gravitational field equations on the brane.[50]It is an interesting topic to explore black holes in the braneworld framework of extra dimensions.In the past few years,several works of brane world black holes as gravitational lenses have been done.[16−18]In this paper,I am going to study the relativistic images produced by a class of brane world black holes,which I call as the Bronnikov–Melnikov–Dehen(BMD)black holes,[51]by using the strong de flection limit method.
The paper is organized as follows:In Sec.2,we obtain the de flection angle formula in the strong de flection limit in BMD metric.In Sec.3,we will discuss some observables.Section 4 is a brief summary.
2 BMD Black Hole Gravitational Lensing in the Strong De flection Limit
BMD black hole is described by the metric[51]
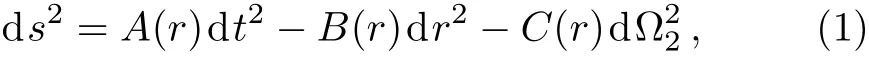
where
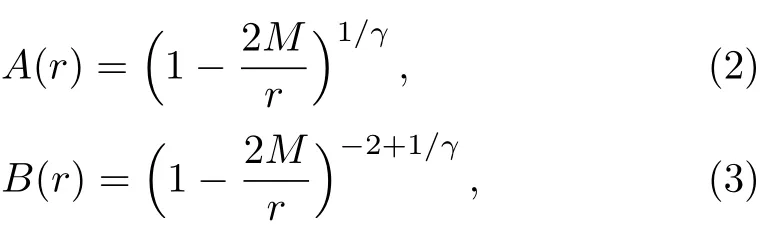
∗Supported by Natural Science Foundation of Education Department of Shannxi Provincial Government under Grant No.15JK1077,and Doctorial Scienti fic Research Starting Fund of Shannxi University of Science and Technology under Grant No.BJ12-02
c○2017 Chinese Physical Society and IOP Publishing Ltd

Hereγ∈ N.anddenotes the metric of a unit twodimensional sphere.Forγ=1,Eq.(1)reduces to the Schwarzschild line element.For convenience,we take the horizon radiusrh=2Mas the measure of distances,then,the line element has the form
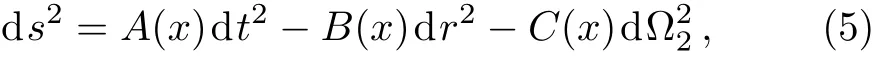
where
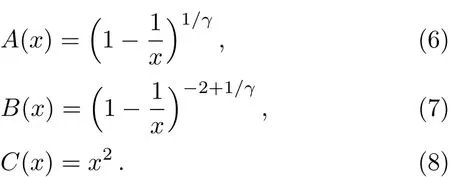
The horizon is located atxh=1.
Consider a photon approaching the BMD black hole from in finity(see Fig.1).In this paper,I shall focus on the situation in which the orbit of the photon is con fined to the equatorial plane,and the lens as well as the observer is in the same orbit plane.From the null geodesics equation,the de flection angle of the photon can be given by[52]
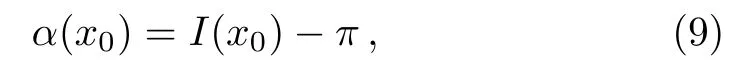
wherex0is the minimum distance of the photon to the black hole and
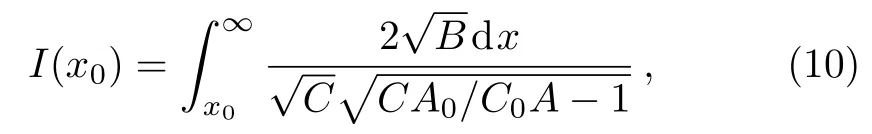
whereA0andC0are the values ofA(x)andC(x)atx=x0,respectively.

Fig.1 A photon approaches near the lens L at a minimum distance x0from the source S with an impact parameter u,and is de flected by an angle α.The observer O sees an image I of the source.DOSis the distance between the observe and the source,DLSis the distance between the lens and the source,and DOLis the distance between the observe and the lens.De fining the line joining the observer and the lens as the optical axis,δ as the angular position of the source and θ as the angular position of the image.

Fig.2 The source(S),The lens(L),the observer(O),the primary image(IP),the secondary image(IS),and the relative images(IR)are shown(I only show the first with clockwise winding and the first with counterclockwise winding).
When we decrease the impact parameteru(and consequentlyx0,see Fig.1),the de flection angle increases.Whenudecreases to a certain value,the de flection angle will exceed 2π,resulting in a complete loop around the black hole(see Fig.2).Decreasingufurther,the photon will wind several times before eventually reaching the observer.Finally,whenx0=xm(corresponding to an impact parameteru=um),the de flection angle will diverge(see below),and the photon will be captured.Herexmis the radius of the photon sphere which is defined as the largest root of the following photon sphere equation[3]

where the prime denotes the differentiation with respect tox.Solving Eq.(11),we get

Following Ref.[3],we can get the de flection angle close to the divergence as

From Fig.1,θ≈ sinθ=u/DOL,therefore,Eq.(13)can be finally transformed to
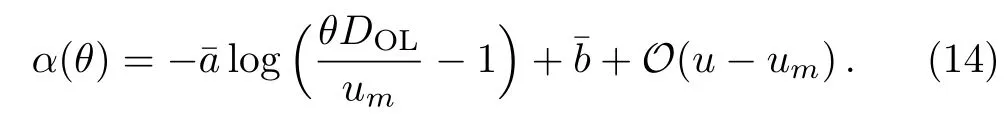
Here the impact parameteruis given by[3]

and its value atxmis

where the subscriptmof a quantity denotes its value atx0=xm.Substituting Eq.(12)into Eq.(16),umcan be rewritten as
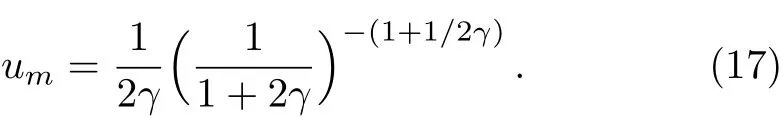
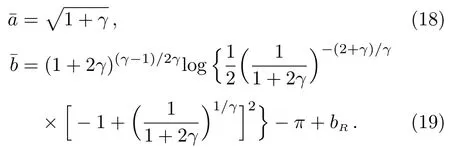
The details of the calculation of the coeきcientsandcan be found in Appendix A.
3 Observables in the Strong De flection Limit
The lensing setup is shown in Fig.1.The lens lies between the observer and the source.(This case is called standard lensing.The other two are called retrolensing in which the source lies the observer and the lens or the observer lies between the source and the lens,see,for example Ref.[19].)The spacetime described by(5)is assumed asymptotically flat,and both the observer and the source are in the flat region.From Fig.1,the Virbhadra–Ellis lens equation[5]
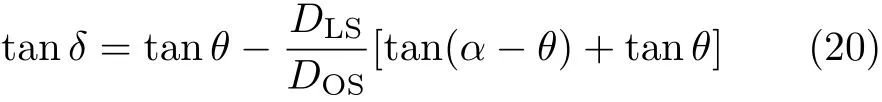
can be obtained.When the source,lens and observer are highly aligned,the relativistic images are most prominent.[4]In this case,bothδandθare small angles andαis close to a multiple of 2π.Writingα=2nπ+ Δαn,wherenis the number of loops that photon winds the lens,and then substituting it into Eq.(20),the lens equation becomes
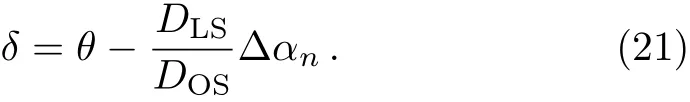
As doing in Ref.[3],using Eqs.(14)and(20),we can obtain three observables as
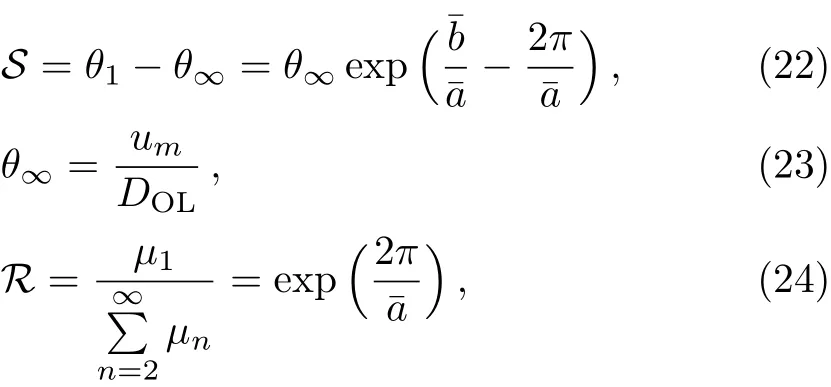
where S is the angular separation between the outermost image and the others,(we consider the simplest situation,in which only the outermost relativistic imageθ1is resolved as a single image,while all others are packaged atθ∞.)and R is the ratio of flux between the first image and all the others.The details of the derivation of these formulae can be found in appendix B.
Equations(22)and(24)can be easily inverted to give

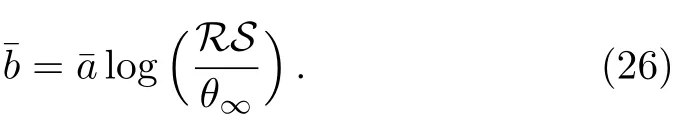
Thus,if observables S,R andθ∞can be obtained,by comparing the experimental coeきcients with those calculated according to different black hole models,we will be able to identify the nature of the black hole lens.
Time delay results are also important for relativistic images.Time delays between ann1-loop and ann2-loop relativistic image can be obtained[53]by using a similar technique of deriving the de flection angle formula in the strong de flection limit given in Appendix A as

wherec2is given by Eq.(A22).
In Table 1,I show the estimates for the lens obervables and de flection angle coeきcients for the central black hole of our galaxy with massM=4.31×106M⊙and the distance from the EarthDOL=8.33 kpc,[54]in the case of BDM braneworld black hole metric.I also show these obtained in the case of Schwarzschild black hole metric[3]and in the cases of two different braneworld black hole metrics,i.e.,the tidal R-N[16−17,55]and the CFM[17,56−59]black hole metrics,for comparison.
The metric describing the tidal R-N braneworld black hole is[16,55]

Equation(28)resembles the R-N black hole metric,but with a positive or negative tidal charge.The observational solar system data on the perihelion shift of mercury gives the tightest restriction||≤7×10−4−6×10−3.[60−62]The formulae of the impact parameter and the coeき-cients of the strong de flection angular for the tidal R-N braneworld black hole can be obtained from those corresponding to the R-N black hole by making the substitutionq−→as[3]
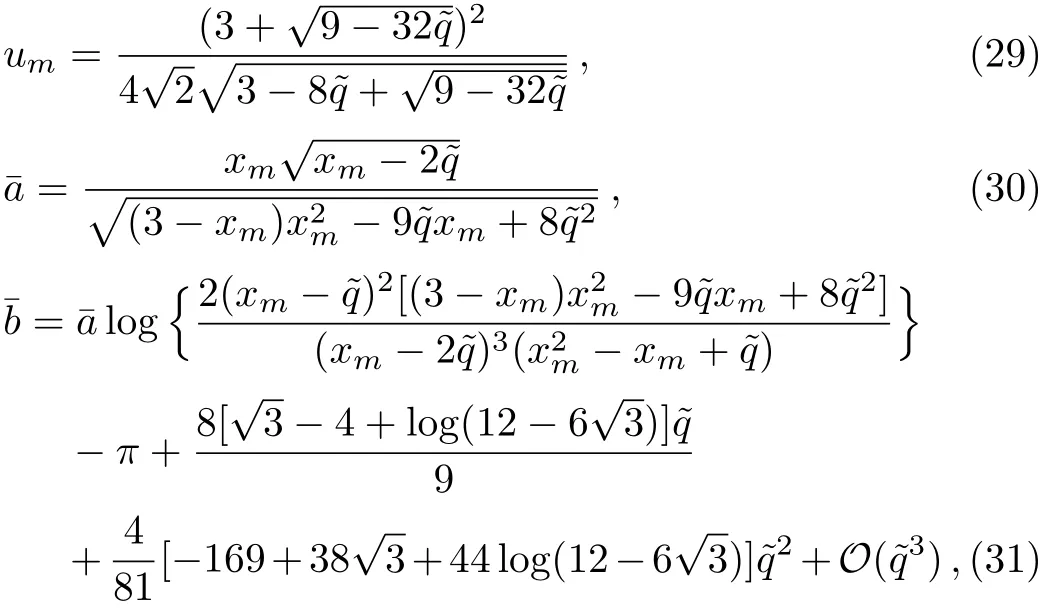
where

The metric describing the CFM black hole is[56−57]ds2

When the parameterη=0,Eq.(33)reduces to the Schwarzschild metric,and short distance tests of Newtonian gravity yield|η| ≤ 10−4from solar system tests.[57−59]The formulae of the impact parameter and the coeきcients of the strong de flection angular for the CFM braneworld black hole can be obtained with the method given in Appendix A as
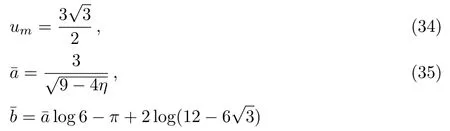
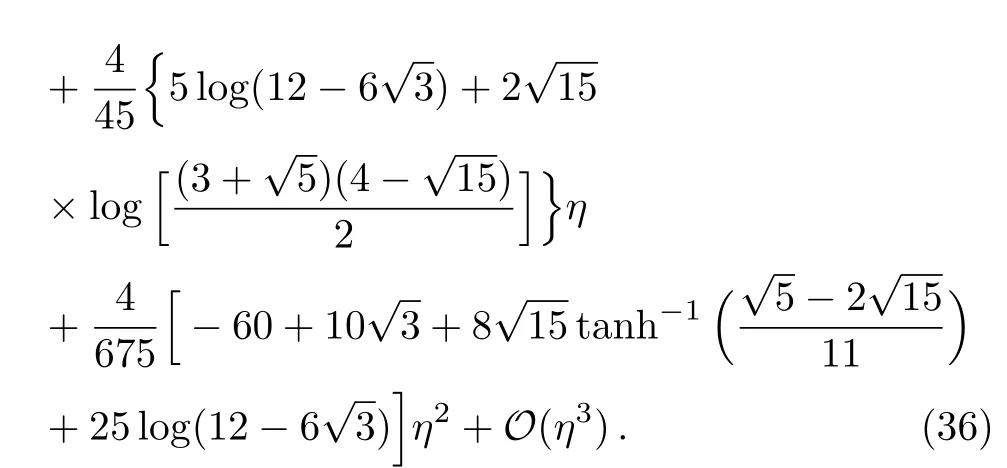
From Table 1,we see that,the parameterγhas signi ficant effects on the de flection angle coeきcients and the observables.With increase ofγ,the angular positionθ∞,the ratio of flux between the first image and all the others Rm,the impact parameterumand the de flection angle coeきcientdecrease,but the angular separation S and the de flection angle coeきcientincrease for the BMD black hole.The relativistic images for the BMD black hole have smallerθ∞,Rmand ΔT2,1,but larger S than those for the Schwarzschild and the other two braneworld black holes with the same mass and distance.
Table 1 Estimates for the lens obervables and de flection angle coeきcients for the central black hole of our galaxy with mass M=4.31×106M⊙and the distance from the Earth DOL=8.33 kpc,in the case of Schwarzschild black hole metric[3]and the cases of three different braneworld black hole metrics,i.e.,the BMD,[51]the tidal R-N[16−17,55]and the CFM[17,56−59]black hole metrics.The unit of θ∞(S)is micro-arcsecond(µas),the unit of ΔT2,1is minute(min),,,Rmand um/RSare dimensionless.Here Rm=2.5log10R is R converted to magnitudes and RS=2 GM/c2.
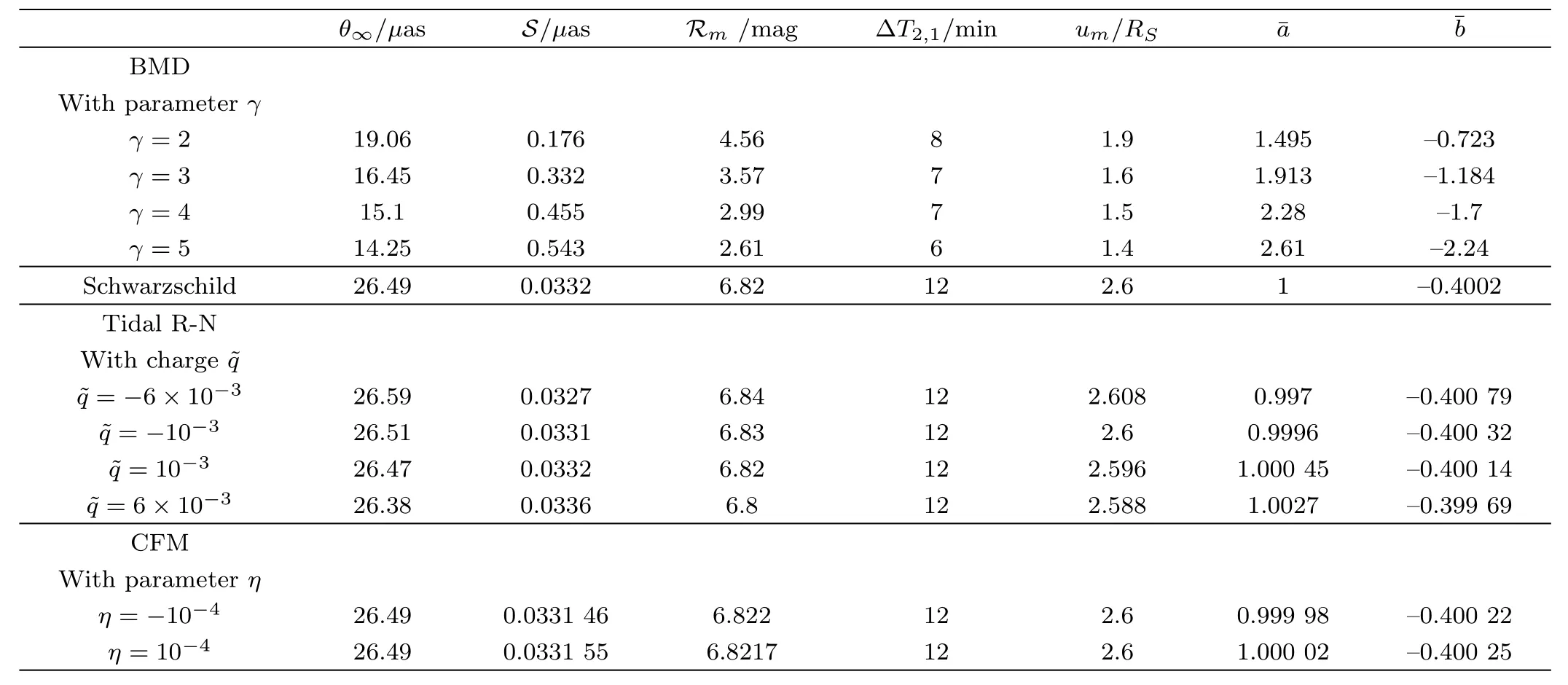
Table 1 Estimates for the lens obervables and de flection angle coeきcients for the central black hole of our galaxy with mass M=4.31×106M⊙and the distance from the Earth DOL=8.33 kpc,in the case of Schwarzschild black hole metric[3]and the cases of three different braneworld black hole metrics,i.e.,the BMD,[51]the tidal R-N[16−17,55]and the CFM[17,56−59]black hole metrics.The unit of θ∞(S)is micro-arcsecond(µas),the unit of ΔT2,1is minute(min),,,Rmand um/RSare dimensionless.Here Rm=2.5log10R is R converted to magnitudes and RS=2 GM/c2.
θ∞/µas S/µas Rm/mag ΔT2,1/min um/RS BMD With parameter γ γ=2 19.06 0.176 4.56 8 1.9 1.495 –0.723 γ=3 16.45 0.332 3.57 7 1.6 1.913 –1.184 γ=4 15.1 0.455 2.99 7 1.5 2.28 –1.7 γ=5 14.25 0.543 2.61 6 1.4 2.61 –2.24 Schwarzschild 26.49 0.0332 6.82 12 2.6 1 –0.4002 Tidal R-N With charge=−6×10−326.590.03276.84122.6080.997–0.400 79 =−10−326.510.03316.83122.60.9996–0.400 32 =10−326.470.03326.82122.5961.000 45–0.400 14 =6×10−326.380.03366.8122.5881.0027–0.399 69 CFM With parameter η η= −10−4 26.49 0.0331 46 6.822 12 2.6 0.999 98 –0.400 22 η =10−4 26.49 0.0331 55 6.8217 12 2.6 1.000 02 –0.400 25
We can find that,for three braneworld black hole gravitational lenses,there are some common properties for the dependence of the de flection angle coeきcients and the observables on the parametersγ,andη.Similar to the case of the BMD black hole,with increase of the parameter(η),S andincrease,and Rmdecreases for the tidal R-N(CFM)black hole.On the other hand,the different effects of the parameter on the de flection angle coeきcients and observables for three braneworld black holes can also be found.Similar to the case of the BMD black hole,with increase of the parameter,θ∞andumdecrease for the tidal R-N black hole,while for the CFM black hole,θ∞andumare independent on the parameterη.In addition,similar to the case of the BMD black hole,with increase of the parameterη,decreases for the CFM black hole,while for the tidal R-N black hole,with increase of the parameter,increases.
Since the resolution of observations of VLBI is about 30µas at present,[63]which is unable to tell difference among all the black holes in the Table 1.I hope that the measurement ofθ∞for the BMD black hole can be made as for the Schwarzschild and the other two braneworld black holes in a not-so-far future since 1µas resolution is in principle attainable by VLBI project.[3]The measurement of the angular separation S for the BMD black hole can also be hopeful to be made with upcoming instruments since Millimetron mission will have an angular resolution of 0.3µas and MAXIM project is expected to have about 0.1µas angular resolution.[15]While the time delay between the second and the first images is of the order of minutes for the central black hole of our galaxy,so we have a little chance to observe such short time delay for a reasonable reference value of time exposure of 10 hours.[53]In order to yield measurable time delays,we need consider more massive black hole than the black hole in the center of our galaxy.In Table 2,I give estimates for the time delay for supermassive black holes located at the center of several nearby galaxies[64]in the case of BMD braneworld black hole metric.Clearly,all of the black holes in Table 2 would yield measurable time delays.

Table 2 Estimates for the time delay for supermassive black holes located at the center of several nearby galaxies in the case of BMD braneworld black hole metric.The unit of ΔT2,1is hour(h),and ΔT2,1(γ)(γ =2,3,4,5)denotes the time delay between the second and the first images in the case of BMD metric(γ=2,3,4,5).
4 Summary
In summary,a class of BMD braneworld black holes are studied as gravitational lenses.I obtain the de flection angle in the strong de flection limit,and also calculate the angular positions and magni fications of relativistic images as well as the time delay between different relativistic images.I compare the results with those obtained for the Schwarzschild black hole,the tidal R-N and the CFM braneworld black holes.It is found that the parameterγhas a signi ficant effect on the observables.With increase ofγ,the angular position of the relativistic imagesθ∞and the relative magni fication Rmdecrease,but the angular separation between the outermost image and the others S increases.The relativistic images for the BMD black hole have smaller angular positionθ∞,relative magni fication Rmand the time delay ΔT2,1,but larger angular separation S than those for the Schwarzschild and the other two braneworld black holes with the same mass and distance.The measurement of the angular positionθ∞and the angular separation S for the black hole at the center of our galaxy can be made in principle with upcoming instruments in the case of BMD braneworld metric.However,in order to yield measurable time delays,we need to consider more massive black hole than the black hole in the center of our galaxy.
Appendix A:Calculation of the De flection Angle in the Strong De flection Limit
We define two variables[51]


wherey0=A0.The integralI(x0)becomes
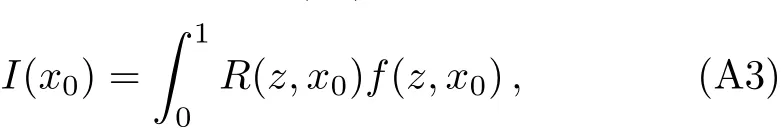
where

Here,it should be stressed that the functions without the subscript 0,B(x),C(x),andA′(x)are evaluated atx=A−1[(1−y0)z+y0].R(z,x0)is regular for all values ofzandx0,whilef(z,x0)is divergent forz→0.In order to find the order of the divergence of(A3),we expand the argument of the square root inf(z,x0)to the second order inz:

where
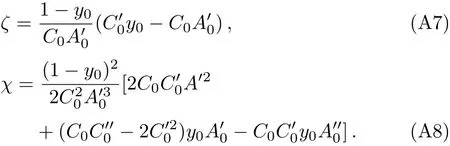
Equation(A7)clearly shows thatζvanishes atx0=xm,sof(z,x0)∝1/zandI(x0)(and consequently the de flection angleα(x0))diverges logarithmically.Then,follow-ing Ref.[51],we split(A3)into two pieces
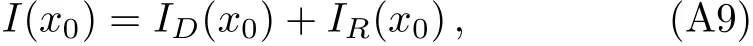
whereID(x0)is divergent,whileIR(x0)is regular,they are
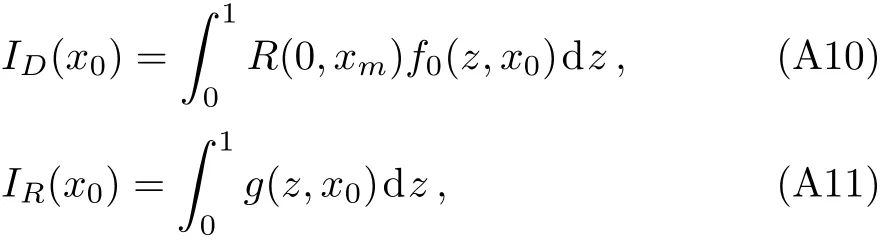
where
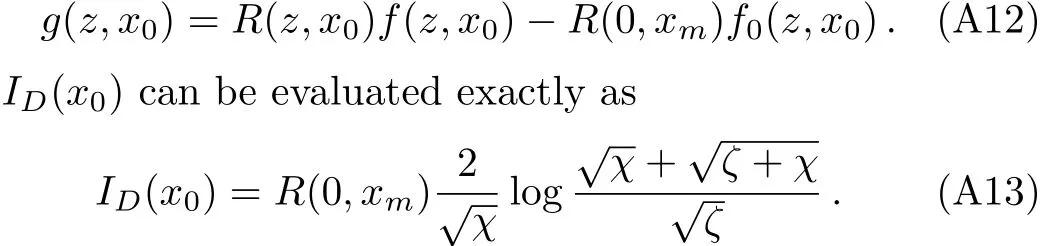
We further expandζin powers of(x0−xm),getting

where
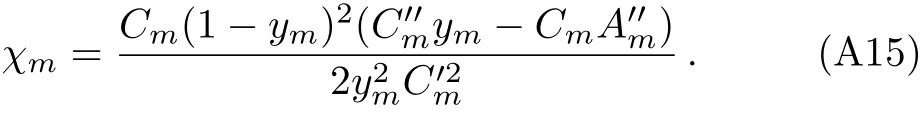
Substituting Eqs.(A14)and(A15)into Eq.(A13),we get
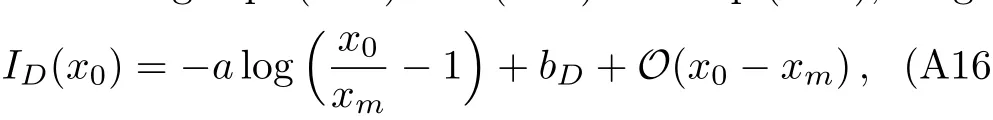
where
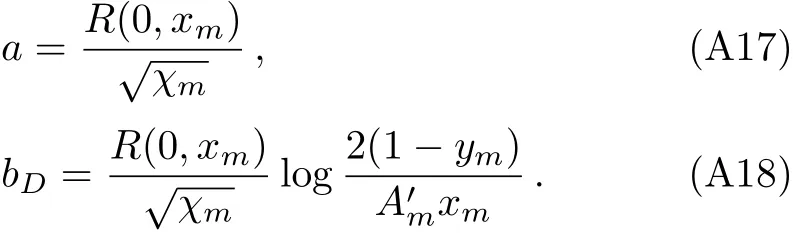
We can also expandg(z,x0)in powers of(x0−xm)to get
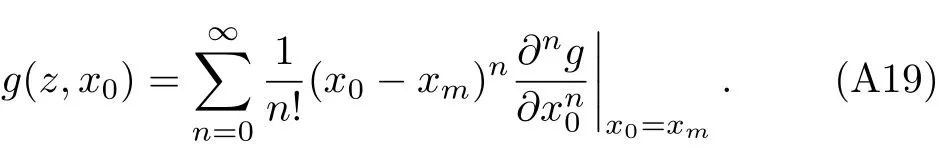
Substituting Eq.(A19)into Eq.(A11),and just retain then=0 term,we get

Expanding Eq.(15),we get
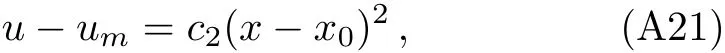

where the coeきcientc2is
Using Eqs.(A21),(A22),andθ≈u/DOL,we can finally express the de flection angle as a function ofθas
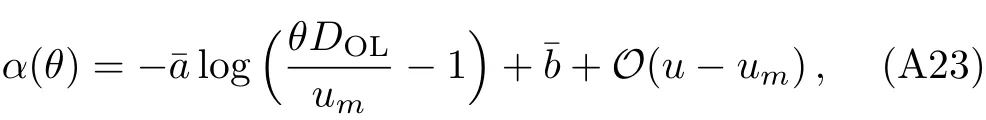
where

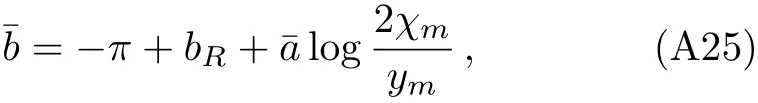
wherebRis defined as

(see Eq.(A20)).
Appendix B:Derivation of the Formulae of Some Observables
Settingαand solving Eq.(14)withα(θ)=2nπ,one can obtain
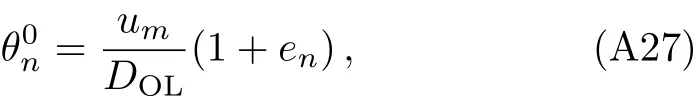
where

Then expandingα(θ)aroundand using Eq.(14),we obtain
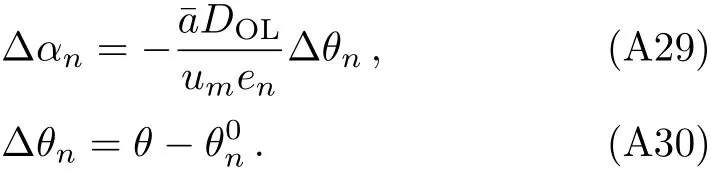
Substituting these equations into Eq.(21),the lens equation becomes
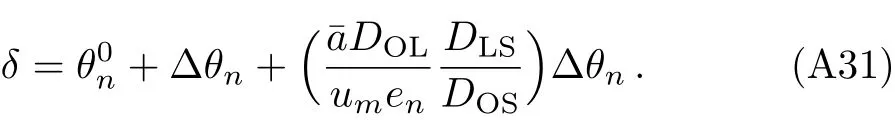
The second term in the righ hand side of Eq.(A31)is negligible when compared to the last term due toum≪DOL.Thus,we get

and the position of ann-loop relativistic image is given
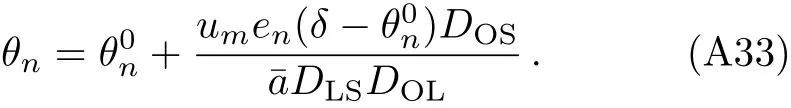
Obviously,the second term in Eq.(A33)is a small correction onWith similar treatment,the position of then-th relativistic image on the opposite side of the source can be also obtained.
The magni fication of then-loop relativistic image is given by
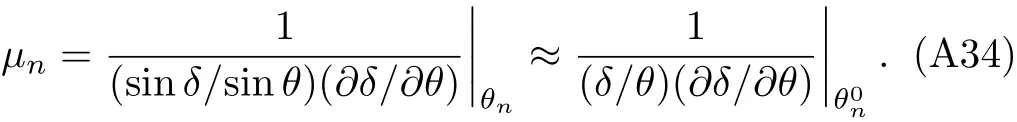
From Eq.(A31)we have
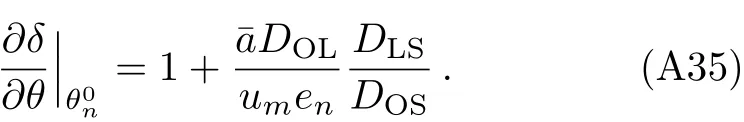
Substituting Eq.(A35)(the first term 1 in Eq.(A35)is small compared to the second and can be neglected)and Eq.(A27)into Eq.(A34),the magni fication can be finally written as
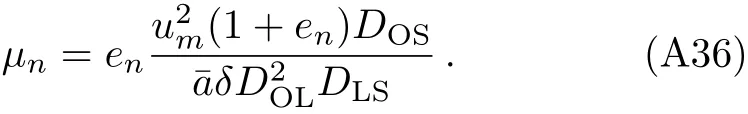
From Eq.(A36)and noticing Eq.(A28),clearly,µndecreases very quickly inn.
From Eq.(A27)(in the limitn−→∞),the minimum impact parameterumcan be expressed as

whereθ∞represents the asymptotic angular position approached by a set of images.(As has been pointed out in Sec.3,we consider the simplest situation,in which only the outermost relativistic imageθ1is resolved as a single image,while all others are packaged together atθ∞.)Two observalbes can be defined as
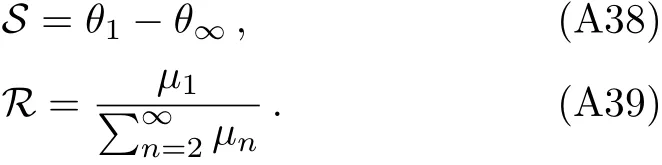
Here S is the angular separation between the outermost image and the others,and R is the ratio of flux between the first image and all the others. Using Eqs.(A27),(A28),and(A37),S can be expressed as
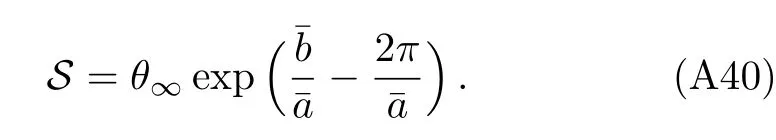
From Eq.(A36),and noticing e≫1 and eis of order one,we can derive out

[1]R.Schödel,et al.,Nature(London)419(2002)694.
[2]P.Schneider,J.Ehlers,and E.E.Falco,Gravitational Lenses,Springer-Verlag,Berlin(1992).
[3]V.Bozza,Phys.Rev.D 66(2002)103001.
[4]K.S.Virbhadra and G.F.R.Ellis,Phys.Rev.D 62(2000)084003.
[5]K.S.Virbhadra and G.F.R.Ellis,Phys.Rev.D 65(2002)103004.
[6]S.Frittelli,T.P.Kling,and E.T.Newman,Phys.Rev.D 61(2000)064021.
[7]C.Darwin,Proc.Roy.Soc.London A 249(1959)180.
[8]J.P.Luminet,Astron.Astrophys.75(1979)228.
[9]S.Chandrasekhar,The Mathematical Theory of Black Holes,Oxford University Press,Oxford(1983).
[10]H.C.Ohanian,Am.J.Phys.55(1987)428.
[11]V.Bozza,et al.,Gen.Rel.Grav.33(2001)1535.
[12]E.F.Eiroa and C.M.Sendra,Class.Quantum Grav.28(2011)085008.
[13]E.F.Eiroa and C.M.Sendra,Phys.Rev.D 86(2012)083009.
[14]E.F.Eiroa and C.M.Sendra,Phys.Rev.D 88(2013)103007.
[15]E.F.Eiroa,Eur.Phys.J.C 74(2014)3171.
[16]R.Whisker,Phys.Rev.D 71(2005)064004.
[17]A.S.Majumdar and N.Mukherjee,Int.J.Mod.Phys.D 14(2005)1095.
[18]E.F.Eiroa and C.M.Sendra,Phys.Rev.D 71(2005)083010.
[19]E.F.Eiroa,Phys.Rev.D 73(2006)043002.
[20]S.S.Zhao and Y.Xie,J.Cosmol.Astropart.Phys.07(2016)007.
[21]S.Chen and J.Jing,Phys.Rev.D 80(2009)024036.
[22]H.Cheng and J.Man,Class.Quantum Grav.28(2011)015001.
[23]C.Ding,S.Kang,and C.Y.Chen,Phys.Rev.D 83(2011)084005.
[24]C.Ding and J.Jing,J.High Energy Phys.10(2011)052.
[25]C.Ding,et al.,Phys.Rev.D 88(2013)104007.
[26]N.Tsukamoto,et al.,Phys.Rev.D 90(2014)064043.
[27]S.W.Wei,K.Yang,and Y.X.Liu,Eur.Phys.J.C 75(2015)253.
[28]H.Sotani and U.Miyamoto,Phys.Rev.D 92(2015)044052.
[29]S.W.Wei,Y.X.Liu,and C.E.Fu,Adv.High Energy Phys.2015(2015)454217.
[30]A.Bhadra,Phys.Rev.D 67(2003)103009.
[31]K.Sarkar and A.Bhadra,Class.Quantum Grav.23(2006)6101.
[32]N.Mukherjee and A.S.Majumdar,Gen.Rel.Grav.39(2007)583.
[33]T.Ghosh and S.SenGupta,Phys.Rev.D 81(2010)044013.
[34]G.N.Gyulchev and I.Zh.Stefanov,Phys.Rev.D 87(2013)063005.
[35]S.Chen and J.Jing,J.Cosmol.Astropart.Phys.10(2015)002.
[36]Y.Huang,S.Chen,and J.Jing,Eur.Phys.J.C 76(2016)594.
[37]V.Bozza,Phys.Rev.D 66(2003)103006.
[38]S.E.Vazquez and E.P.Esteban,Nuovo.Cimento.B Ser.119(2004)489.
[39]V.Bozza,et al.,Phys.Rev.D 72(2005)083003.
[40]V.Bozza,Phys.Rev.D 78(2008)063014.
[41]S.Chen and J.Jing,Class.Quantum Grav.27(2010)225006.
[42]S.Chen,Y.Liu,and J.Jing,Phys.Rev.D 83(2011)124019.
[43]S.Chen and J.Jing,Phys.Rev.D 85(2012)124029.
[44]S.Wang,S.Chen,and J.Jing,J.Cosmol.Astropart.Phys.11(2016)02.
[45]K.S.Virbhadra and C.R.Keeton,Phys.Rev.D 77(2008 124014.
[46]J.Man and H.Cheng,J.Cosmol.Astropart.Phys.11(2014)025.
[47]X.Lu,F.W.Yang,and Y.Xie,Eur.Phys.J.C 76(2016)357.
[48]A.Chamblin,S.W.Hawking,and H.S.Real,Phys.Rev.D 61(2000)065007.
[49]R.Maartens,Living.Rev.Rel.7(2004)7.
[50]C.S.J.Pun,Z.Kov´acs,and T.Harko,Phys.Rev.D 78(2008)084015.
[51]K.A.Bronnikov and V.N.Melnikov,Phys.Rev.D 68(2003)024025.
[52]S.Weinberg,Gravition and Cosmology:Principles and Applications of the General Theory of Relativity,Wiley,New York(1972)
[53]V.Bozza and L.Mancini,Gen.Rel.Grav.36(2004)435.
[54]S.Gillessen,et al.,Astrophys.J.Lett.707(2009)L114.
[55]N.Dadhich,et al.,Phys.Lett.B 487(2000)1.
[56]R.Casadio,A.Fabbri,and L.Mazzacurati,Phys.Rev.D 65(2002)084040.
[57]R.Casadio,Phys.Rev.D 69(2004)084025.
[58]C.M.Will,Theory and Experiment in Gravitational Physics,2nd ed.,Cambridge University Press,Cambridge(1993).
[59]C.M.Will,Living.Rev.Rel.4(2001)4.
[60]C.G.Bohmer,T.Harko,and F.S.N.Lobo,Class.Quantum Grav.25(2008)045015.
[61]C.G.Bohmer,et al.,Class.Quantum Grav.27(2010)185013.
[62]X.M.Deng and Y.Xie,Mod.Phys.Lett.A 31(2016)1650021.
[63]A.E.Broderick,et al.,Astrophys.J.784(2014)7.
[64]D.Richstone,et al.,Nature(London)395(1998)A14.
杂志排行
Communications in Theoretical Physics的其它文章
- Instability Analysis of Positron-Acoustic Waves in a Magnetized Multi-Species Plasma
- Dual Solutions of MHD Boundary Layer Flow of a Micropolar Fluid with Weak Concentration over a Stretching/Shrinking Sheet
- Numerical Investigation of Micropolar Casson Fluid over a Stretching Sheet with Internal Heating
- Dynamics of Optical Bistability with Kerr-nonlinear Blackbody Radiation Reservoir
- Collisions and Trapping of Time Delayed Solitons in Optical Waveguides with Orthogonally Polarized Modes∗
- Special Property of Group Velocity for Temporal Dark Soliton∗
