Dynamics of Optical Bistability with Kerr-nonlinear Blackbody Radiation Reservoir

Yasser A.Sharaby

Suez University,Faculty of Sciences,Physics Department,Suez,Egypt

1 Introduction

Optical bistability(OB)is a phenomenon generated in non-equilibrium systems due to both,nonlinearity and feedback.[1−3]It has been investigated both experiementally and theoretically in Rnig and Fabry–Perot cavities.[4−22]OB has potential applicationsin various fieldsofopticalcomputation and communications[7−8,15−18,23−25]since,it exhibits two output states for one input field. Such a bistable device may be used for optical transistors,switching,memories and quantum logic gates.Optical bistability can be realized in normal[1−2,8−18]and squeezed vacua radiation reservoirs,[26−33]in both Fabry–Perot and ring cavity configurations.

Recently,OB has been studied for a system of twolevel atoms placed in a ring cavity in the presence of Kerr nonlinear blackbody(KNB)radiation reservoir.[34]It is shown that OB can be observed with lower cooperative parameter compared with that in normal[8]and squeezed[29]vacua.Further,the OB with KNB reservoir[34]offeres the possibility of thermal switching device near resonance conditions at fixed input field.Moreover,critical slowing down of the thermal switching effects has been stuided recently[35]by perturbing the relative temperature in the vicinity of its critical value.It is observed that,the OB device switches faster with KNB radiation reservoir than with other NV(normal vacuum),SV(squeezed vacuum)and TF(thermal field)reservoirs.Also,the thermal switching can be enhanced by increasing the relative temperatureTb.Very recently,[36]we have shown that in the presence of inhomogeneous broadening of atomic linewidth,bistability area increases with relative temperatureTband thermal switching occurs over a larger range ofTbin comparsion with homogeneous broadening of atomic linewidth.[34]

In the case of KNB,the resulting radiation produce some photon pairs,and unpaired photons forming a nonpolariton,a quasiparticle that contributes to the free thermal(blackbody)radiation.[37]These photon pairs are formed by the presence of the phonons at temperature below a certain transition temperature,so the KNB can be found in a squeezed thermal state.A KNB radiation reservoir can be acheived by simply filling the interior of a blackbody cavity with a Kerr-like medium(usually a nonlinear crystal in rectangular or cylindrical kind of shape)under the condition that the thermal radiation and the Kerr-like medium are in thermal equilibrium with each other and maintain a fixed temperature for the cavity.[37−39]In the case of normal blackbody,the state of the electromagnetic field is replaced by photon pair state in the KNB case during matter- field interaction.This leads to a replacment of in finite energy of the vacuum field by a finite energy of phton pairs.[38−39]Some important studies in the presence of the KNB reservoir are:the suppression of spontaneous emission from a two-level atom below a transition temperature[39]and the preservation of quantum entanglements of atoms.[40]

In earlier works[10,41−42]a linear stability analysis for the absorptive optical bistability in a ring cavity showed that under certain conditions,part of the upper branch of the hysteresis curve is unstable.Such a system can operate as a transformer of continuous wave light into pulsed light,where a self pulsing oscillation occurs with a period equal to the cavity round-trip time.This analysis was generalized in the dispersive OB case[43](see Refs.[17–18]and references therein).Another mechanism of in-stability was theoretically studied by Ikedaet al.,[44−47]where periodic instabilities and chaotic behavior could occur in optical bistable two-level system in a ring cavity with time delay effects,when the propagation time of the radiation field from the output-to the input-end is longer than the atomic decay time.This instability can lead to period doubling and chaos as reported[6]for Fabry–Perot cavity containing sodium atoms in the absorptive OB case.Single mode instabilities ranging from gain assisted laser systems[48]to passive two-level optical bistable systems have been investigated[49]and revisited with more details.[50−53]Effects of the squeezed vacuum on the dynamic behavior of two-level OB systems have been discussed in Ref.[30].Novel instability of OB systems has been examined in Ref.[54]for thin material with thickness much smaller than the wavelength for pure absorptive OB csae.Another new type of instability occurs in three-level atomic medium,[55]which does not require the condition of existence of finite detuning and occurs without coupling to multiple modes of the cavity field in contrast to that occurs in the two-level atomic bistability.[56]Further,the instability examination in the lower cooperative branch for the Λ-andV-atomic systems inside a double-cavity[57]showed that it is due to the leakage of population from the coherently prepared lower atomic levels.This leakage occurs via spontaneous emission into the ground state leading to instability in the lower cooperative branch.Such instability occurs only in the V-type system wherein incoherent decay coupling of the pair of ground states is essential to obtain instabilities in the cooperative branch.

In normal vacuum,the dynamics of OB outside the rotating wave approximation has been examined recently.[58]In this study,the optical bistable behavior routes from periodic to chaotic behavior,with spiking generation,by decreasing the input field.In addition,the atomic detuning causes bifurcation from chaotic to self pulsing and vice versa.Optical chaos generated in nonlinear optical systems is applicable for communication information at high data rates[59]and useful in applications of random number generation.[60−61]

In this paper,we further extend the work reported in Ref.[34]to investigate the dynamical behavior of homogeneously broadened two-level atomic systems placed in an optical ring cavity,in the presence of KNB radiation reservoir.We show that the dynamics of the system and chaos are sensitively dependent on the input field amplitude,the relative temperature and the atomic- field detuning parameter.

The paper is organized as follows:In Sec.2,we review the Maxwell–Bloch equations for the OB system in contact with KNB reservoir.Section 3 presents the computational results,followed by a conclusion in Sec.4.

2 Model Review

Consider a homogeneously broadened two-level atomic medium of lengthLplaced inside an optical ring cavity driven by a coherent field and exposed to KNB radiation reservoir.The Maxwell–Bloch equations are given as,[34]

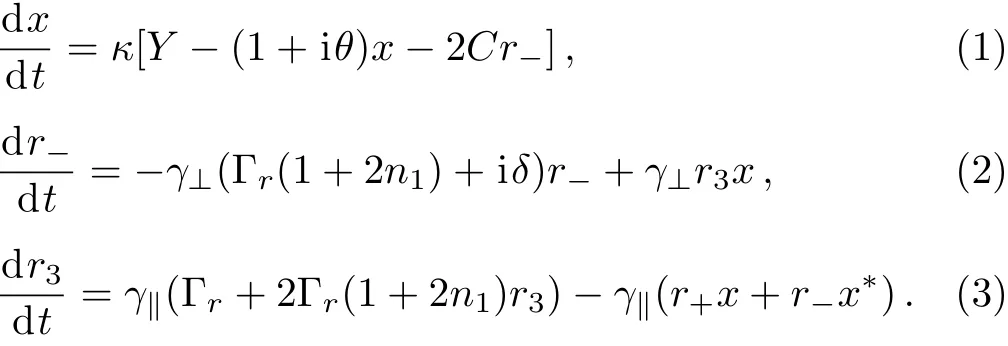
Here,n1=(eħω/kBT− 1)−1is the average photon number of the heat bath(thermal reservoir)maintained at fixed temperatureTB,kBis the Boltzman consant andδ=(ωo−ωL)/γ⊥is the normalized atom- field detuning,ωLis the input field frequency,γ⊥is the transverse atomic decay rate for the polarization atomic component andγ‖is the longitudinal atomic decay rate for the population difference.C=αL/2Tis the cooperativity parameter,withαis the absorption coeきcient andTis the transmissivity of the output mirror.x,Yare the normalized transmitted and incident field amplitudes,respectively.r±(t)are the mean values of the quadratic atomic polarization components andr3(t)is the mean atomic population.θ=(ωc−ωL)/κis the normalized cavity detuning withωccavity mode frequency,κ=cavity decay constant.The relative decay rateΓris defined asΓr=γKNB/γ⊥withγKNBis the atomic decay rate in the presence of KNB radiation reservoir.In the KNB reservoir case,[39−40]the radiation is in a squeezed thermal state below a transition temperatureTc(dependent on the Kerr nonlinear crystal)which results in atomic spontaneous emission supression due to formation of phonon pairs via lattice vibrations.AboveTc,the KNB behaves like a normal blackbody(ordinary thermal radiation of temperatureTB).The formation of photon pairs is physically understood as follows:[37]the photons in the blackbody radiation experience an effective interaction by excahnge of phonons.In this case,the photon is surrounded by a phonon cloud which couples with another photon to form photon pairs.Thus,photons with opposite wave vectors and spins are bound into pairs,and unpaired photons are tranformed into quasiparticle nonpolaitons forTB＜Tc.Accordingly,Γris given as,[39]

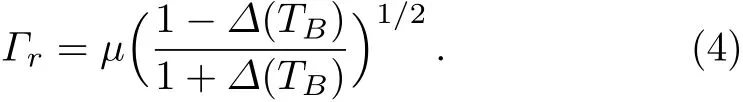
WithΔ(TB)/=0:(TB＜TC)is the order parameter for pairing of photons,and has the approximate form,[39]

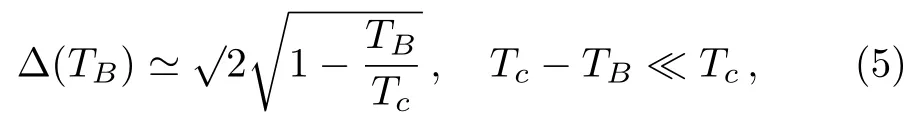
which is monotonically decreasing function of the temperatureTB,vanishes at the transition temperatureTcand yieldsΓr/µ=1,µis the refractive index of the medium of KNB,Tb=TB/Tcis the relative temperature of the KNB reservoir.Δ(TB)=0 for normal blackbody thermal reservoirTB≥Tcand normal vacuum case whereΓr=1.Tcis determined explicity from the equation,[34]

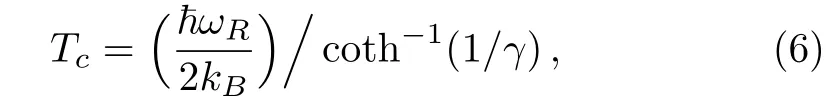
withγ＜1 is a dimensionless parameter,termed as coupling constant related to the characteristic of Kerr nonlinear crystal placed in the cavity,Xc= ħωR/2kBTcandωRis the frequency of the Raman-active mode of the crystal.[39]

In the steady state case,Eqs.(1)–(3),give the inputoutput relationship,

Instabilities of single mode laser one-photon systems have been investigated in 1970’s,[48]which showed the analogy of the chaotic behavior between laser systems and fluids(modelled by Lorenz equations).The chaos in nonlinear optical cavities results either from nonlinear lightmatter interaction[44]or from nonlinear coupling between optical modes as in laser cavities.[62]The conditions of self-pulsing have been discussed in both absorptive and dispersive regimes in ring cavity[42−43]and the route from self-pulsing to chaos has been reported for large parametersC=70000,δ=374,θ=340.[56]Further,the nonlinear dynamics of two photon laser system was investigated and showed chaotic,period doubling,stable and bistable states[53]with chaos suppressed by initial atomic populations,atomic coherence and injected classical field.Optical instabilities most likely[49−52]arise when the atomic system interacts with(large)multimode field leading to chaos and self-pulsing or with intense single cavity mode field that saturates the collection of atoms in the absorptive OB.When the system in the vicinity of the unstable region of the upper branch of OB curve,either it transfers to the lower branch or exhibits either periodic(self pulsing)oscillatory behavior or non-periodic chaotic behavior.The analytical study of instability[17−18]for absorptive and dispersive bistability shows that the instability of the upper branch may exist if at least one of the off-resonant modes are unstable.

Here,we investigate the nonlinear dynamical behavior of the OB system,Eqs.(1)–(3),within the RWA in the dispersive OB case when the atomic polarization variables are eliminated adiabatically.In this adiabatic case,the atomic relaxation time for the atomic polarization components is shorter than the other characteristic times(γ⊥≫γ‖,κ,κθ,κC)of the system.Hence by substutiting the stationary value ofr−from Eq.(2)into Eqs.(1),(3)and then expressing the normalized output fields as,x=u+ivand we obtain the following system of ODEs:

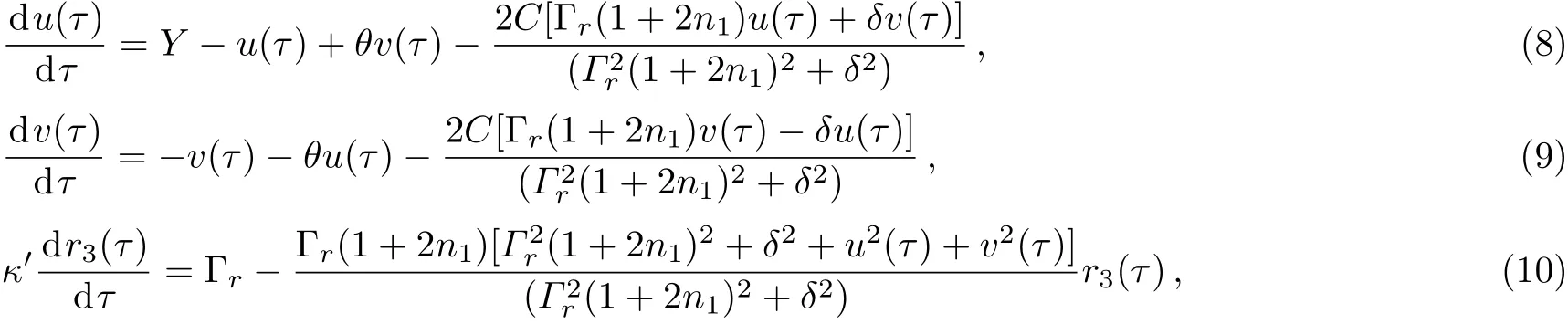
where,κ′=κ/γ‖,τ=κt.Equations(8)–(10)are solved numerically with the initial conditions by using the standard Runge–Kutta method to show the transition between dynamical states by varying the relative temperatureTb.

3 Computational Results

Nonlinear systems that display period doubling and chaos are sensitive to the system parameters and essentially show four mo des of operations:chaotic,stable,periodic,and quasiperiodic.The effect of relative temperature(Tb)on the steady state relation(the output field|x|against the input fieldY),in the dispersive case,for large set of paramters(cf Refs.[42–43]),δ=220,θ=250 and fixedC=60000(Fig.1)show that the bistable area decreases with increasing the relative temperatureTb.Linear stability analysis around the stationary state shows that,points on the upper branch of the bistable behavior are unstable and the associated instability arises with opposite signs of the detuning parameters(δθ＜0)and multiple periods of unstable points occur for large cooperativity(C＞300).[49]

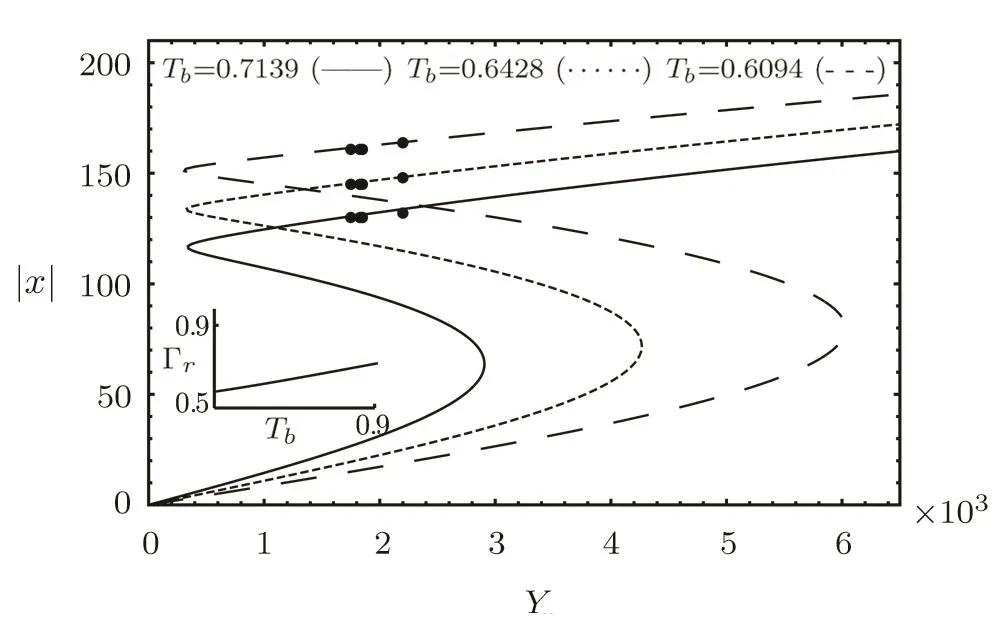
Fig.1 The output field|x|against the incident field Y for δ=220, θ=250,C=60000,and different relative temperature Tb=0.7139,0.6428,and 0.6094 equivalent to Γr=0.9,0.7,0.6,respectively.Inset shows the relative decay parameter Γragainst the relative temperature Tb.

In the normal vacuum case,OB behaves nonlinearly exhibiting stable,periodic,quasiperiodic and choas modes according to the values of the system parameters.[49,56]We calculate the bifurcation diagram of the maximum peak of the output field(Max|x|)as a function of relative temperatureTbto analyze the transition between the dynamical states.The transition between dynamical states when varying the relative temperatureTbis displayed by the bifurcation diagram(Fig.2),for fixed

and input field valueY=1750.In this bifurcation diagram,the route of periodic(including stable,period doubling)to chaotic behavior is observed by decreasing the relative temperatureTbover range

For decreasing the relative temperatureTb,the system display chaos over the relative temperature range

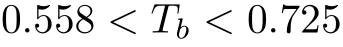
and followed by periodic behavior again over range

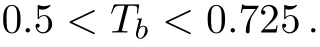
These opposite two routes occur over a range of 0.5＜Tb＜0.9.Thus,the OB with KNB is very rich in dynamics,such that the device can operate at specified temperatureTb,as a pulsed device with regular or irregular osillations.

Fig.2 Bifurcation diagram representing the maximum value of the output field|x|against the relative temperature Tbfor fixed C=60000,κ′=0.25,δ=220,θ=250,and Y=1750.

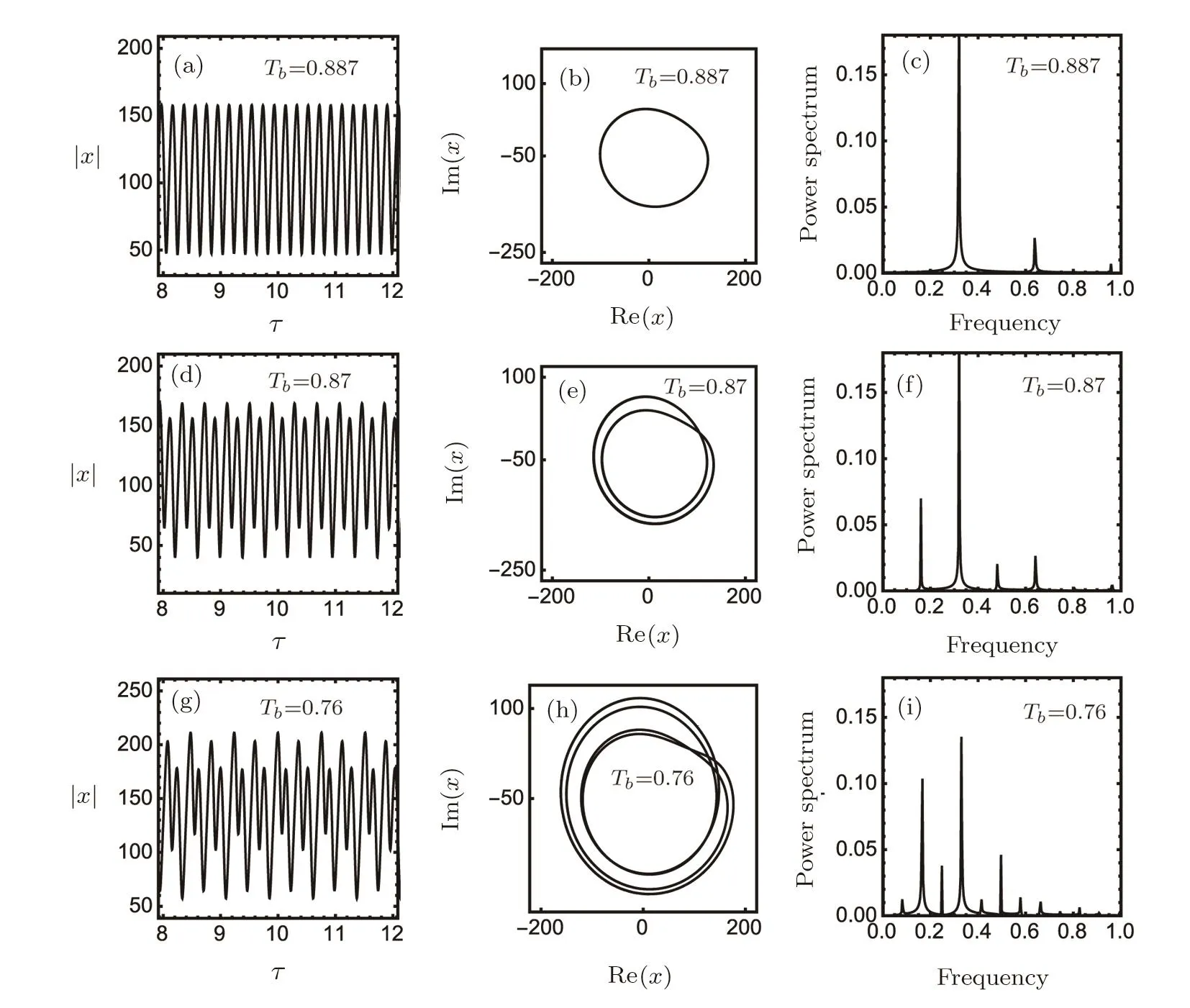
Fig.3 (a)Self pulse oscillations for the output field|x|in the adiabatic case against the time τ for C=60000,δ=220,θ=250,Y=1750 and Tb=0.887.(b)The corresponding phase-space representation(Im(x),Re(x))of the output field.(c)Power spectrum for|x|.(d)–(f)Same as(3(a)–3(c))but with Tb=0.87.(g)–(i)Same as(3(a)–3(c))but with Tb=0.76.

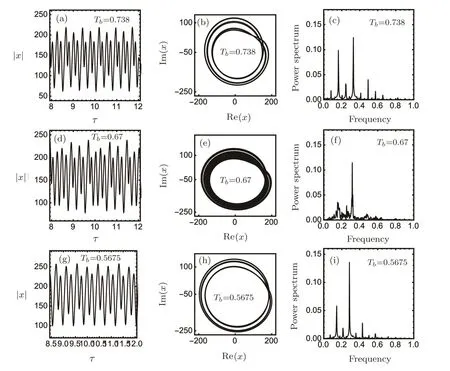
Fig.4 Same as Fig.3 but with Tb=0.738,0.76,0.5675.

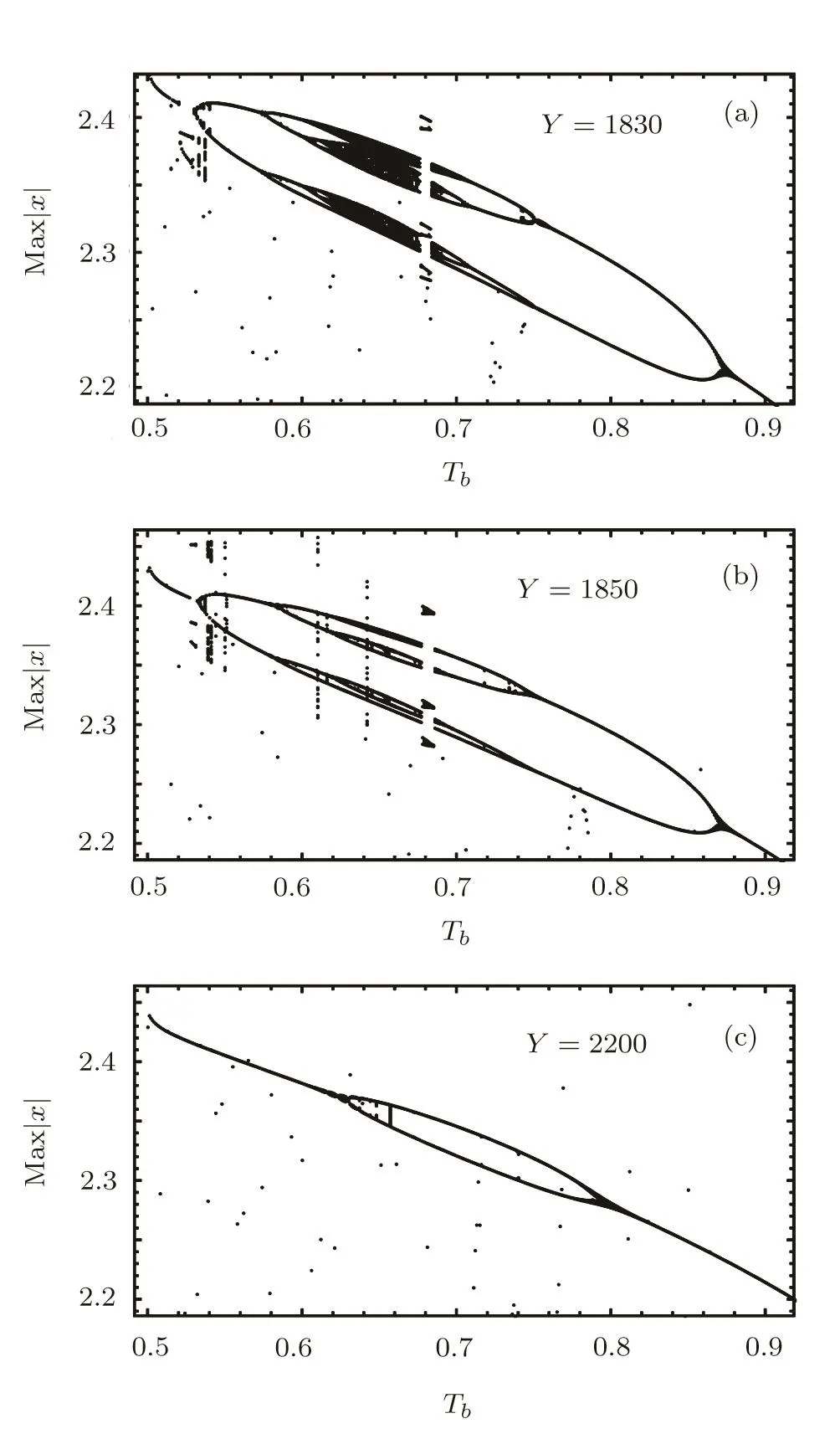
Fig.6 (a)Bifurcation diagram representing the maximum value of the output field|x|against the relative temperature Tbfor fixed C=60000,δ=220,θ=250,and Y=1830.(b)As(6(a))but with Y=1850.(c)As(6(a))but with Y=2200.

The transition between dynamical states can be shown by integrating the system of normalized coupled equations(8)–(10)for fixed values ofδ=220,θ=250,C=60000,κ′=0.25,Y=1750 and different values ofTb.For differentTbvalues,the time-dependent of the output field|x|and the phase portrait(Im(x),Re(x))and power spectrum diagrams of the input intensities are plotted respectively in Figs.3–5 for fixed parameters of the system.Periodic behavior for the output field along the upper branch of the OB curve is shown in Fig.3 for different values of the relative temperatureTb.AtTb=0.887,(Figs.3(a)–3(c)),a single period(Fig.3(a))is exhibited in phase space(Fig.3(b))and con firmed as a prominent sigle peak in the power spectrum(Fig.3(c)).Decreasing the relative temperatureTbto 0.87,the double period occurs in Figs.(3(d)–3(e))and two prominent peaks in Fig.(3f).Further decrease in the relative temperatureTbto 0.76(Figs.3(g)–3(i))and 0.738(Figs.4(a)–4(c))shows the occurance of period four.When the relative temperatureTbis reduced to 0.67 the system starts to perform more periods and finally chaotic behavior occurs(Figs.4(d)–4(f)).After a range of chaotic behavior over the relative temperature range(0.558＜Tb＜0.725),a decrease in the relative temperature toTb=0.5675,causes periodic behavior with period 4(Figs.4(g)–4(i)),double period at valuesTb=0.557,0.539(Figs.5(a)–5(f)),and a single period atTb=0.518(Figs.5(g)–5(i)).

Increasing the input fieldYalong the upper branch toY=1830(Fig.6(a)),the chaotic range over the relative temperature range shrinkes with more shrinking atY=1850(Fig.6(b)),but bifurcation to instability modes still exist.Chaos vanishes with further increase of the input fieldY=2200(Fig.6(c)),and the system shows only stable and two-periods.Note that every point in the bifucation diagram represents a peak of the oscillations.For fixedY=1750,the system routes from chaotic to aperiodic behavior and again to chaotic behavior by varying the atomic detuning(Fig.7).

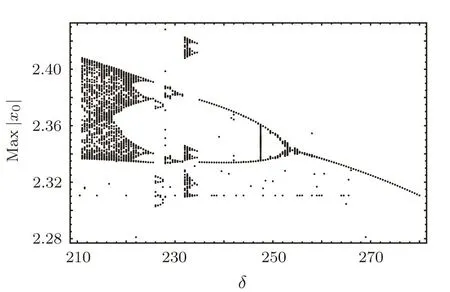
Fig.7 Bifurcation diagram representing the maximum value of the output field|x|against the atomic detuning δ for fixed values of parameters C=60000,κ′=0.25,θ=250,Y=1800,and Tb=0.6094.

4 Conclusion

We have investigated the nonlinear dynamics of OB system phenomenon with homogeneously broadened twolevel atomic medium interacting with a single mode of the ring cavity in the presence of a Kerr-nonlinear blackbody(KNB)radiation reservoir.The relative temperatureTb(ratio between the temperature of the reservoirTBand the transtion temperatureTc)affects signi ficantly the steady state behavior of the system.In addition,the relative temperatureTbgives rise to rich dynamical behavior via bifurcation diagrames of the output field withTb.The system bifurcates from periodic to chaotic behavior by the decreasing the relative temperature at fixed input field.The choas region extends over the range 0.558＜Tb＜0.725 followed by periodic behavior with further decrease in the relative temperature.The chaotic behavior that exhibited for input field(Y=1750)shrinks and vanishes by increasing the input field(atY=2200).The vanishing of chaos over a certain range of relative temerature is desirable,sometimes,in optical bistable systems which implies stablization for steady states.ForY=2200 the system shows only a single period and two periods over the entire range of relative temperatureTb.The transition between the dynamical states routes from regular(self-pulsing)to irregular(chaos)oscillations by varying the atomic detuning as seen in the bifurcation diagram of the output field against the atomic detuning.

Future investigation in the same model may include the effect of:cavity time delay effect(cf Ref.[58])and inhomogeneous broadening on the dynamics of the sysytem(cf Ref.[36]).

The author acknowledges fruitful discussions with Prof.S.Shoukry Hassan(University of Bahrain).

[1]H.M.Gibbs,Optical Bistability Controlling Light With Light,Academic Press,Inc.,Orlando,FL(1985)p.481.

[2]A.Joshi and M.Xiao,Controlling Steady-State and Dynamical Properties of Atomic Optical Bistability,World Scienti fic,Singapore(2012).

[3]Chunfei Li,Nonlinear Optics:Principles and Applications,Shanghai Jiao Tong University Press,Shanghai and Springer Nature Singapore Pte Ltd.(2017).

[4]A.Szöke,V.Daneu,J.Goldhar,and N.A.Kurnit,Appl.Phys.Lett.15(1969)376.

[5]S.L.McCall,Phys.Rev.A 9(1974)1515.

[6]H.M.Gibbs,S.L.McCall,and T.N.C.Venkatesan,Phys.Rev.Lett.36(1976)1135.

[7]H.M.Gibbs,S.L.McCall,and T.N.C.Venkatesan,Opt.News 5(1979)6.

[8]R.Bonifacio and L.A.Lugiato,Opt.Commun.19(1976)172.

[9]R.Bonifacio and L.A.Lugiato,Phys.Rev.A 18(1978)1129.

[10]R.Bonifacio and L.A.Lugiato,Lett.Nuovo Cimento 21(1978)517.

[11]S.S.Hassan,P.D.Drummond,and D.F.Walls,Opt.Commun.27(1978)480.

[12]E.Abraham,R.K.Bullough,and S.S.Hassan,Opt.Commun.29(1979)109.

[13]E.Abraham,S.S.Hassan,and R.K.Bullough,Opt.Commun.33(1980)93.

[14]E.Abraham and S.S.Hassan,Opt.Commun.35(1980)291.

[15]E.Abraham and S.D.Smith,J.Phys.E 15(1982)33.

[16]E.Abraham and S.D.Smith,Rep.Prog.Phys.45(1982)815.

[17]L.A.Lugiato,inProgress in Optics,ed.E.Wolf,Vol.21 North Holland,Amsterdam(1984)pp.71-183.

[18]L.A.Lugiato and L.M.Narducci,in:Fundamental Systems in Quantum Optics,eds.J.Dalibard,J.M.Raimond,and J.Zinn-Justin,Elsevier Sci.Publ.,Amsterdam(1992)pp.942-1043.

[19]B.S.Wherrett and P.Chavel,(Eds.),Optical Computing,Inst.Physics Publ.,Bristol(1995).

[20]J.N.Lee,(Ed.)Design Issues in Optical Processing,Cambridge University Press,Cambridge,UK(1995).

[21]D.G.Feitelson,Optical Computing,MIT Press,MA(1988).

[22]C.M.Bowden,M.Ciftan,and H.R.Robl(Eds),Optical Bistability,Plenum Press,NY(1981).

[23]M.J.Adams,A.Hurtado,D.Labukhin,and I.D.Henning,Choas 20(2012)037102.

[24]A.M.C.Dawes,L.Illing,S.M.Clark,and D.J.Gauthier,Science 308(2005)672.

[25]Q.Guo,X.Zhao,H.Zhao,and V.Chigrinov,Opt.Lett.40(2015)2413.

[26]S.M.A.Maize,M.F.M.Ali,and S.S.Hassan,Nonlinear Optics 8(1994)218.

[27]J.Bergou and D.Zhao,Phys.Rev.A 52(1995)1550.

[28]Z.Chen,C.Du,S.Gong,and Z.Xu,Phys.Lett.A 259(1999)15.

[29]S.S.Hassan,H.A.Batra fi,R.Saunders,and R.K.Bullough,Eur.Phys.J.D 8(2000)403.

[30]H.A.Batra fi,S.S.Hassan,R.Saunders,and R.K.Bullough,Eur.Phys.J.D 8(2000)417.

[31]M.F.M.Ali,S.S.Hassan,and S.M.A.Maize,J.Opt.B:Quantum Semiclass.Opt.4(2002)388.

[32]S.S.Hassan and Y.A.Sharaby,Eur.Phys.J.D 30(2004)393.

[33]L.P.Maia,G.A.Prataviera,and S.S.Mizrahi,Phys.Rev.A 69(2004)053802.

[34]A.Joshi,Y.A.Sharaby,and S.S.Hassan,Opt.Commun.359(2016)387.

[35]Y.A.Sharaby,S.S.Hassan,and S.Lynch,Optik 127(2016)10195.

[36]Y.A.Sharaby,Nonlinear Optics and Quantum Optics 48(2016)79.

[37]Z.Cheng,Phys.Lett.A 291(2001)4.

[38]Z.Cheng,Phys.Lett.A 331(2004)170.

[39]M.Yin and Z.Cheng,Phys.Rev.A 78(2008)0638290.

[40]Q.F.Xu,X.Z.Hui,J.N.Chen,and Z.Cheng,Eur.Phys.J.D 66(2012)66.

[41]S.L.McCall,Appl.Phys.Lett.32(1978)284.

[42]R.Bonifacio,M.Gronchi,and L.A.Lugiato,Opt.Commun.30(1979)129.

[43]L.A.Lugiato,Opt.Commun.33(1980)108.

[44]K.Ikeda,H.Daido,and O.Akimato,Phys.Rev.Lett.45(1980)709.

[45]K.Ikeda and O.Akimoto,Phys.Rev.Lett.48(1982)617.

[46]Ikeda,Opt.Commun.30(1979)257.

[47]H.M.Gibbs,F.A.Hopf,D.L.Kaplan,and R.L.Shoemaker,Phys.Rev.Lett.46(1981)474.

[48]H.Haken,Phys.Lett.A 53(1975)77.

[49]L.A.Orozco,H.J.Kimble,A.T.Rosenberger,L.A.Lugiato,M.L.Asquini,M.Brambilla,and L.M.Narducci,Phys.Rev.A 39(1989)1235.

[50]S.M.A.Maize,Nonlinear Optics and Quantum Optics 35(2006)331.

[51]S.M.A.Maize and G.Ibrahim,Nonlinear Optics and Quantum Optics 35(2006)285.

[52]S.M.A.Maize,G.Ibrahim,and M.F.M.Ali,Nonlinear Optics and Quantun Optics 36(2007)117.

[53]Xie Xia,Huang Hong-Bin,Qian Feng,et al.,Commun.Theor.Phys.45(2006)1042.

[54]L.A.Lugiato and F.Prati,Phys.Rev.Lett.104(2010)233902.

[55]H.A.Babu and H.Wanare,Phys.Rev.A 88(2013)023814.

[56]L.A.Lugiato,L.M.Narducci,D.K.Bandy,and C.A.Pennise,Opt.Commum 43(1982)281.

[57]H.A.Babu and H.Wanare,Phys.Rev.A 83(2011)033819.

[58]Y.A.Sharaby,S.Lynch,A.Joshi,and S.S.Hassan,J.Nonlinear Opt.Phys.Mater.23(2014)1950019.

[59]D.J.Gauthier,Science 279(1998)1156.

[60]J.T.Gleeson,Appl.Phys.Lett.81(2002)1949.

[61]T.Stojanvoski,J.Pihl,and L.Kocarev,IEEE.Trans.Circuits Syst.I 48(2001)382.

[62]M.Virtu,K.Panajotov,H.Thienpoint,and M.Sciamanna,Nature Photon 7(2013)60.