Collisions and Trapping of Time Delayed Solitons in Optical Waveguides with Orthogonally Polarized Modes∗

2018-01-22HuanZhou周欢JinHuaLi李金花KwokWingChow周国荣ShaoRongXiao肖韶荣andTingTingSun孙婷婷SchoolofPhysicsandOptoelectronicEngineeringNanjingUniversityofInformationScienceandTechnologyNanjing0044China

Communications in Theoretical Physics 2017年4期

关键词：金花

Huan Zhou(周欢),Jin-Hua Li(李金花),,† Kwok-Wing Chow(周国荣),Shao-Rong Xiao(肖韶荣), and Ting-Ting Sun(孙婷婷)School of Physics and Optoelectronic Engineering,Nanjing University of Information Science and Technology,Nanjing 0044,China

2Department of Mechanical Engineering,University of Hong Kong,Hong Kong SAR 999077,China

1 Birefringence and Soliton Collisions

TheconventionalnonlinearSchrödingerequation(NLSE)for localized modes in fibers,or related optical waveguides,might need modi fication if birefringence is taken into account.Evolution and dynamics of orthogonally polarized modes are governed by the coherently coupled NLSEs.[1−2]

whereAandBare the slowly varying amplitudes for each polarization mode.The symbolsσ,λwill represent the ratio of cross phase modulation(XPM)to self phase modulation(SPM),and the effect of four-wave mixing(FWM)respectively.The parameterλis related to the polarization susceptibility ratio,andσ=2/3=1−λfor isotropic silica fiber.The parameterγ,a difference of wave numbers,measures the degree of birefringence.The second derivative terms relate the group velocity dispersion in the temporal setting,but model diffraction in the spatial context.zis distance andtis retarded time/distance in fiber/bulk material respectively.The mismatch in group velocities has been assumed to be negligible.

It is instructive to derive the non-dimensional system of Eq.(1)and Eq.(2)from the physical,governing equations for isotropic silica fiber:[2]

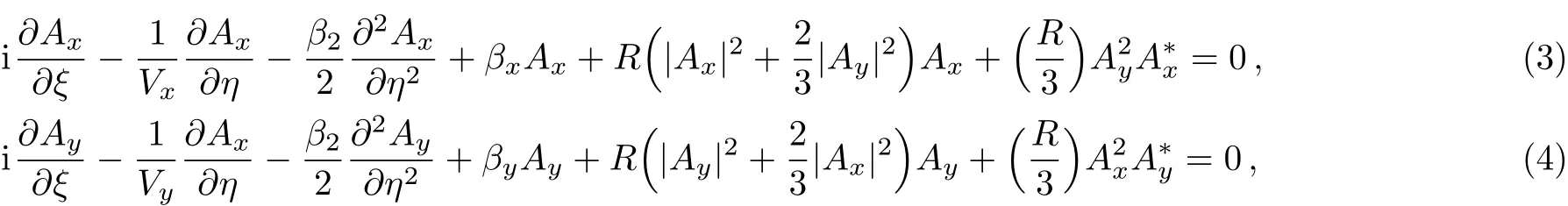
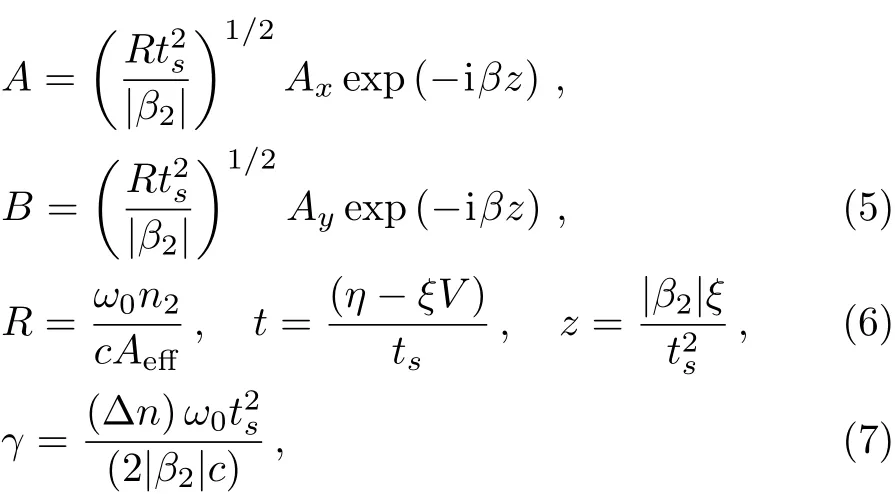
with whereAx,Ayare the electric fields,VxandVyare group velocity ofxandypolarizations respectively.For weak birefringence case considered here,Vx=Vy=V.ω0,n2,ts,c,Aeff,β2,Δnare the mean optical frequency,nonlinear refractive index,temporal width of the fundamental soliton of NLSE,velocity of light,effective core area,group velocity dispersion coeきcient and difference in refractive indices(birefringence)respectively.Hence the employed values ofδ,σ,λfollow and withc=3 × 108ms−1,ω0∼1014Hz,ts∼O(10−13→ 10−12)s,|β2|∼ 20 ps2·km−1,Δn∼O(10−7→ 10−5),a non-dimensionalγcan indeedattain order one values.[3]

Collisions of solitons[4−6]have been studied intensively under various simplifying assumptions:

High birefringence limit–The FWM terms oscillate rapidly and will be neglected on averaging.Collisions of vector solitons as a function of the difference in group velocities(the ‘walk off’speed)exhibit a fractal structure.[7−9]

Manakov model–Perturbation theory can be developed in the vicinity of the integrable regime,namely,the Manakov model,where the self and cross phase modulation coeきcients are equal(and FWM terms are ignored or small).[10]Variational approximations prove to be useful in numerical simulations.[11−12]Conditions to minimize collisions among multiple solitons are considered.[13−14]

Dependence on cross phase modulations and higher order effects– The interactions of solitons with different coeきcients of cross phase modulation have been studied.[15−16]Third order dispersion has also been incorporated.[17]Relation between cross Raman scattering and optical phase-shift switches is studied.[18]Models combining dispersion management,third order dispersion and birefringence can be constructed.[19]Elliptic birefringence has also been investigated.[20]

Experiments–Change of polarization states[21]and trapping of localized pulses[22−23]are observed in experiments with fibers.Parallel works on slab waveguides,e.g.AlGaAs,are also performed.[24]

2 Collisions and Trapping of Solitons

The main goal is to simulate collisions of time delayed solitons with neither the high nor the low birefringence approximations being invoked.The conventional high birefringence approximation will ignore the FWM term,while a low birefringence approximation might drop the term involvingγin Eq.(1)and Eq.(2).System of Eq.(1)and Eq.(2)is now solved numerically with the standard split step Fourier schemes with the initial condition(z=0):

where Δ is the initial separation of the pulses.These solitons will be termed ‘time delayed’solitons in this paper.If Δ is zero,the solitons are launched simultaneously,and there is a sizable literature.[1]If Δ is suきciently large,the two pulses will propagate individually without any interactions.We shall study intermediate values of Δ.

The most remarkable phenomenon is that the two pulses can trap each other in a suitable range of parameter values:

(i)Dependence on the birefringence parameter

If the value of the birefringence parameter(γ)is extremely small,the pulses undergo one to several‘collision(s)’,and then the main portions of the pulses separate in opposite directions(Fig.1).For small but finite values ofγ,after one or two brief collision(s),the pulses travel in space and remain trapped to each other(Fig.2).For suきciently large values ofγ,this trapping effect is lost,and the two initial pulses evolve into two pairs of counter-propagating pulses.The main portions in the two waveguides move in opposite directions,and there are weak remnants of the trapping phenomenon just barely visible(Fig.3).

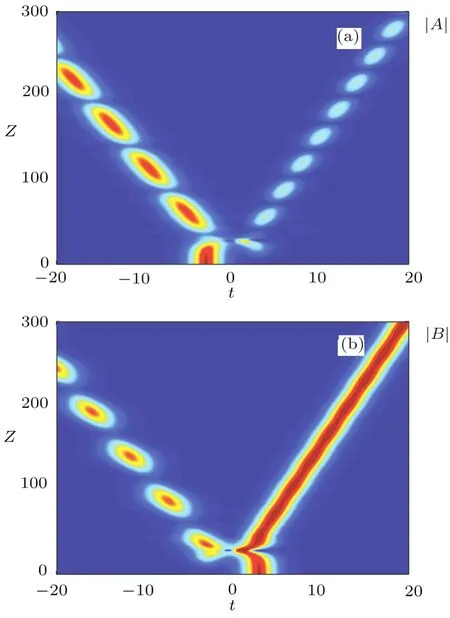
Fig.1 (Color online)Pulses A and B moving in opposite directions after the initial collision(s)with γ=0.01,λ =1/3,and Δ =6.

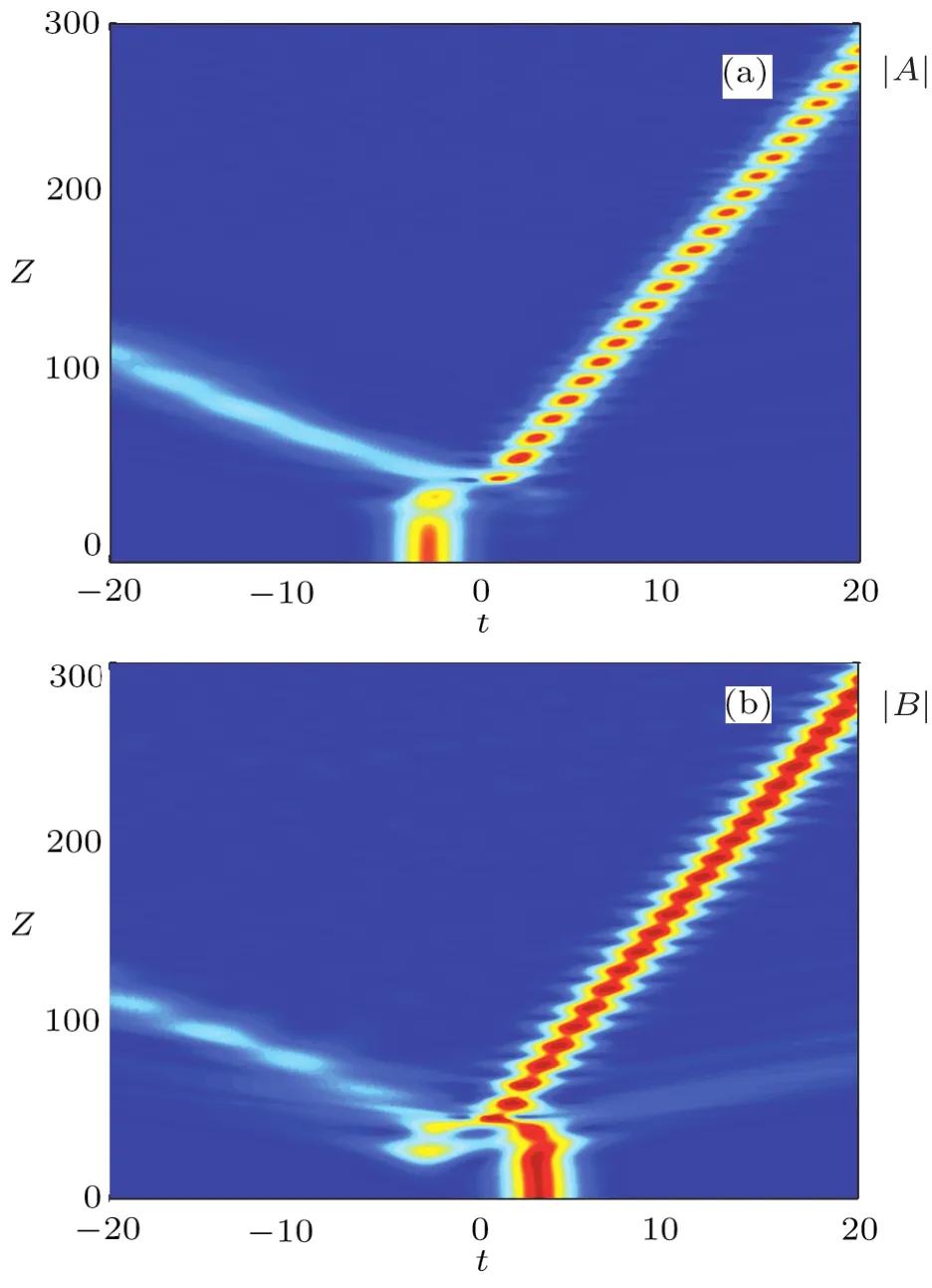
Fig.2 (Color online)Trapping of pulses A and B with γ =0.1,λ =1/3,and Δ =6.

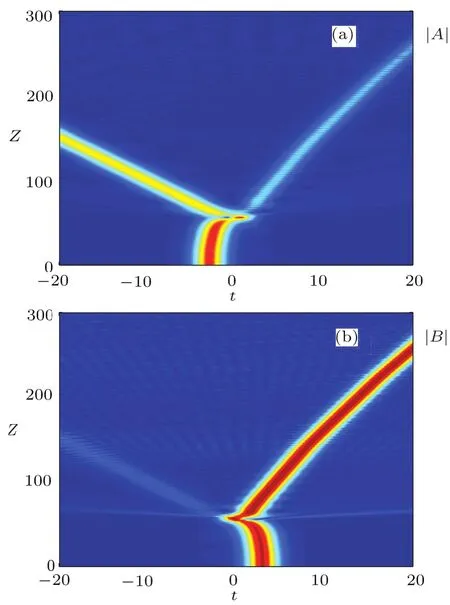
Fig.3 (Color online)Pulses A and B moving in opposite directions after the initial collision(s)with γ=0.5,λ =1/3,and Δ =6.

(ii)Dependence on the four-wave mixing parameter

For fibers,σ=2/3,λ=1/3 is a reasonable choice,but for elliptical polarization or bulk materials,the choice for the coeきcients of FWM and XPM will be much wider due to the absence of Kleinmann symmetry.For bulk materials/spatial solitons,tin(1)becomes a spatial coordinate,but still the main interest is to understand the principles of nonlinear science.

For illustrative purpose,we still considerσ=1 −λ,but will varyλto study the presence of trapping.For smallλ,the pulses move in opposite directions(Fig.4),but for largerλ,trapping will occur(Fig.5).

(iii)Distance of initial collision

If solitons are used in optical fibers for communications,the initial collision distance would be relevant to the quality of signal transmission.This distance is insensitive to changes inγbut depends strongly on values ofλand Δ.It is worthwhile to pursue an additional veri fication and the variational reduction is employed.The variational method reduces the in finite dimensional model(1)to a low-dimensional dynamical system.Such reduction technique is commonly used in the study of general Hamiltonian partial differential equations.[25−26]The Hamiltonian system(1)can be reformulated in terms of a Lagrangian

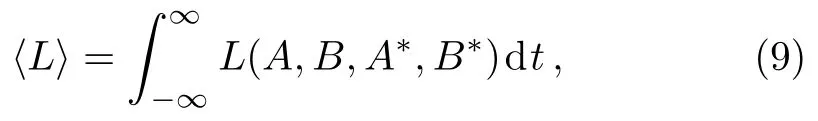
with Lagrangian density

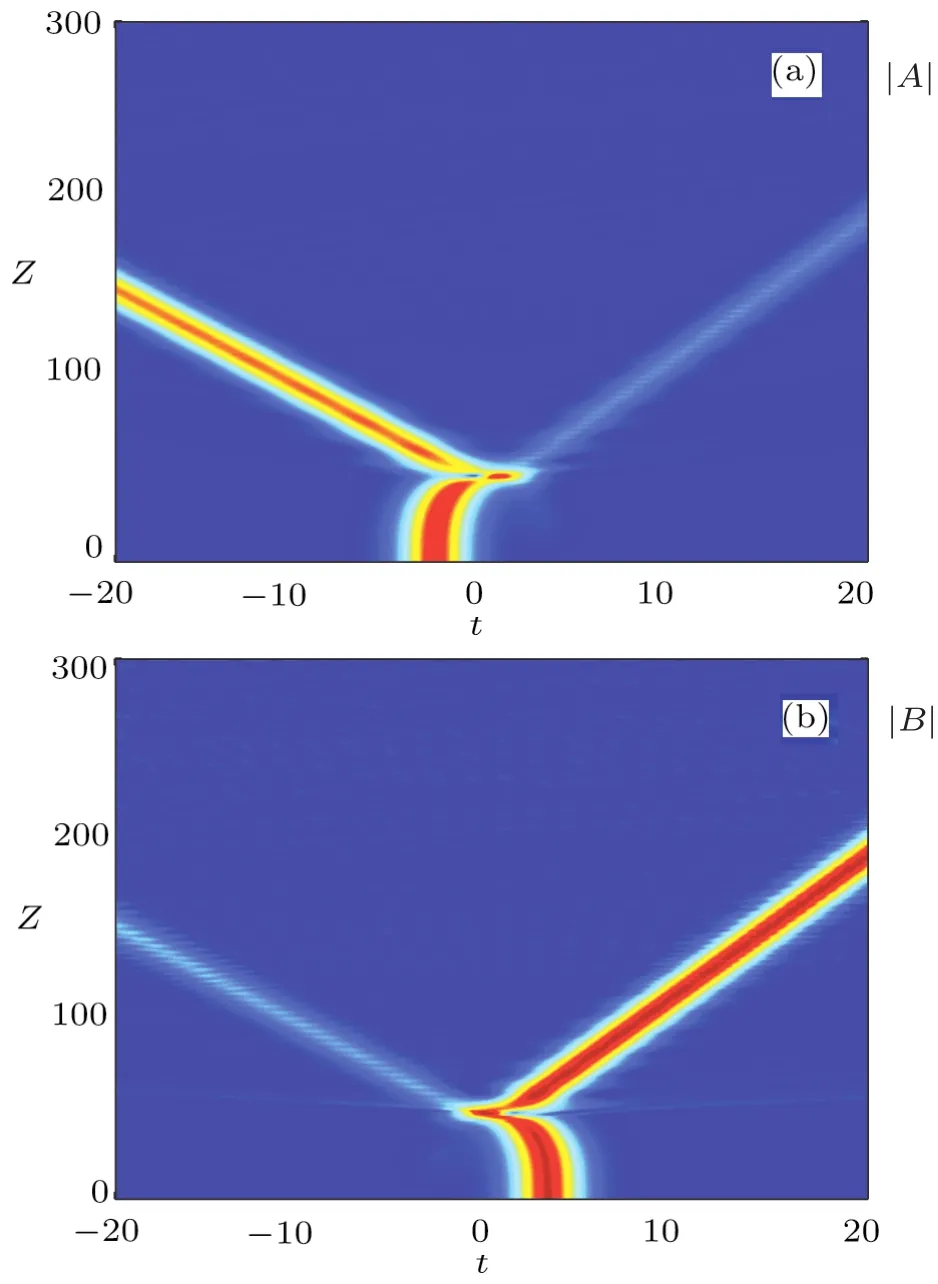
Fig.4 (Color online)Pulses A and B moving in opposite directions after the initial collision(s),γ=0.5,λ=0.2,and Δ=6.

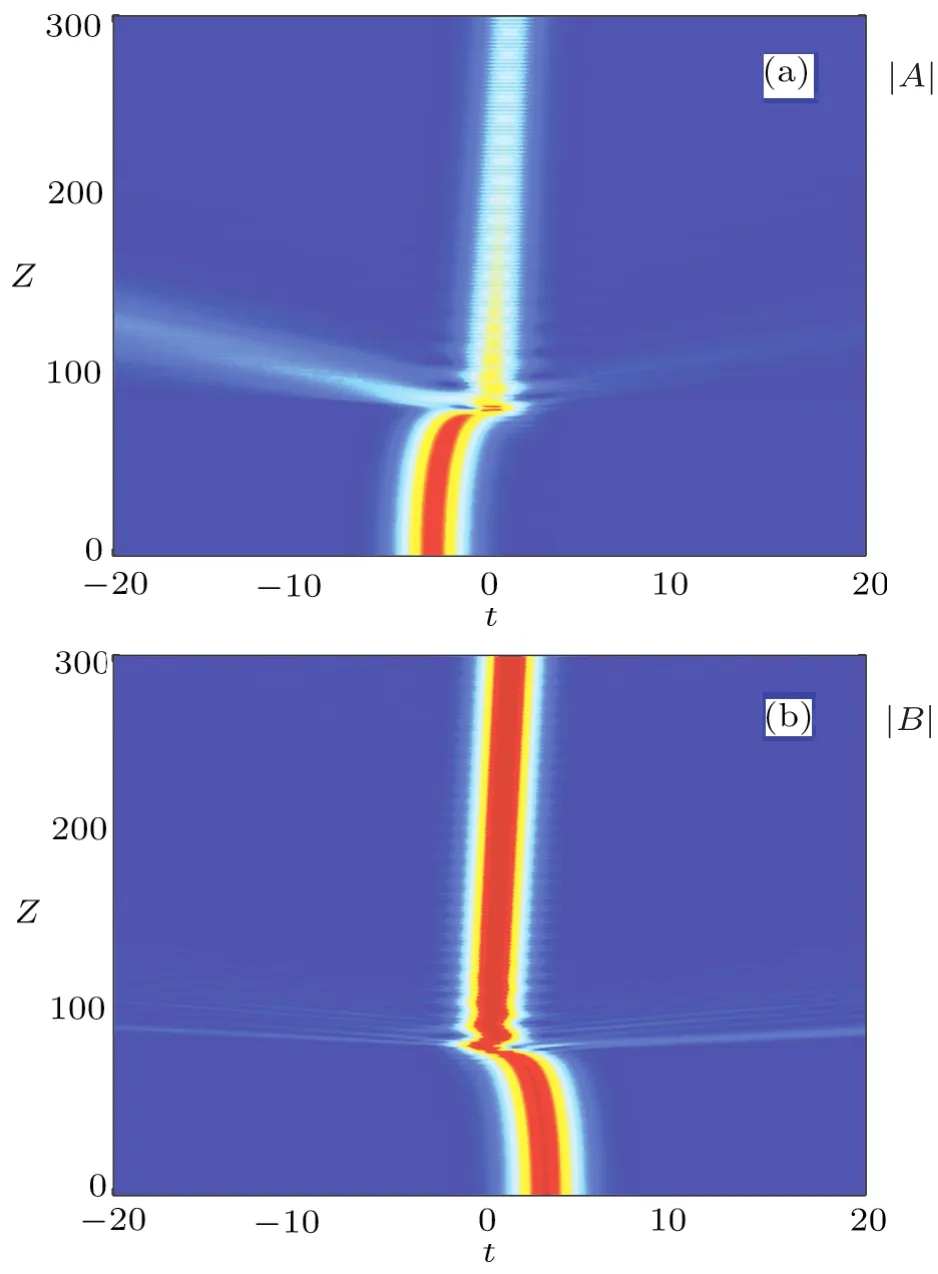
Fig.5 (Color online)Trapping of pulses A and B,γ =0.5,λ =0.6,and Δ =6.

In the reduction procedure we assume a chirped hyperbolic secant ansatz,

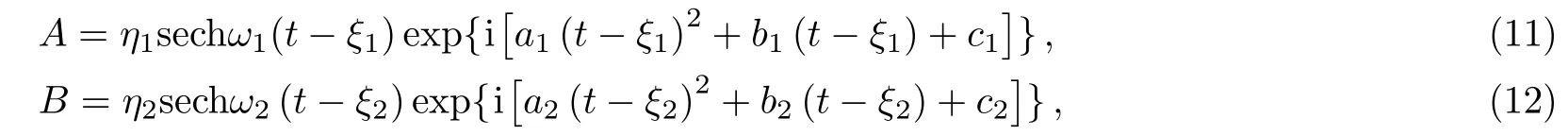
where real functionsη1,2,ω1,2,ξ1,2,a1,2,b1,2,andc1,2represent the amplitudes,reciprocals of widths,center positions,chirps,phase velocities,and absolute phases respectively.The Euler–Lagrange equation

with respect to each of the pulse parametersρithen yields a system of first order evolution equations.Collision distance is obtained by solving these first order equations numerically.If the pulses are placed suきciently far apart initially,it is well-known that they will not interfere.[1]For intermediate values of Δ,the pulses should interact each other as shown by Fig.6 for Δ =5.As Δ increases,the initial collision distance has increased dramatically as shown by Fig.7 for Δ=7.While variation reduction should give respectable results when the true dynamics as governed by Eq.(1)and Eq.(2)remains close to that of the chosen ansatz.In the case where either of the fieldsAorBsplits into multiple pulses,the reduced Lagrangian fails to model the actual evolution accurately.Nevertheless,the variational method serves as an excellent tool for the present purpose,namely,to predict the distance before the first collision,as the pulses have not started to disintegrate yet.Figure 8 shows that the variational technique and results from the full numerical simulations agree perfectly well for a fairly wide range of Δ.

Fig.6 (Color online)Trapping of pulses A and B(smaller Δ),γ =0.5,λ =0.7,and Δ =5.

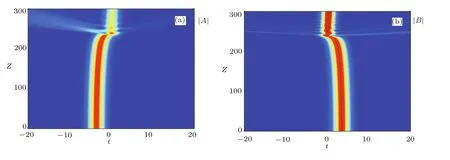
Fig.7 (Color online)Trapping of pulses A and B(larger Δ),γ =0.5,λ =0.7,and Δ =7.

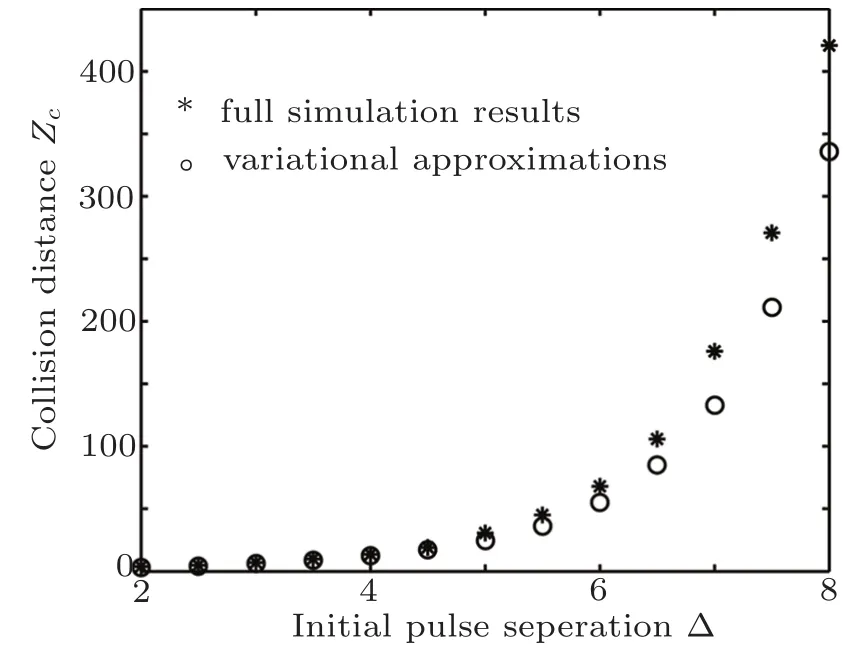
Fig.8 Dependence of the collision distance Zcof solitons on the initial pulse separation Δ with γ =0.5, λ =1/3.

3 Conclusion

Motivated by recent theoretical[1−2]and experimental[21−24]works,collisions of time delayed solitons are studied,but neither the high birefringence nor the low birefringence approximations are invoked.Trapping of solitons are observed for small values of the birefringence parameter and large values of the four-wave mixing parameter.Distance to the first collision is relevant in applications to fiber optics communications,and this distance depends strongly on the initial pulse separation.Variational approximation is employed to provide an additional check and the results agree very well with those from the full numerical simulations.

[1]G.P.Agrawal,Nonlinear Fiber Optics,Academic,San Diego(2007).

[2]S.Wabnitz,E.M.Wright,and G.I.Stegeman,Phys.Rev.A 41(1990)6415.

[3]H.S.Chiu and K.W.Chow,Phys.Rev.A 79(2009)065803.

[4]D.Yang,S.Y.Lou,and W.F.Yu,Commun.Theor.Phys.60(2013)387.

[5]X.Wang and Y.Chen,Commun.Theor.Phys.61(2014)423.

[6]X.Y.Tang and S.Y.Lou,Commun.Theor.Phys.44(2005)583.

[7]J.Yang and Y.Tan,Phys.Rev.Lett.85(2000)3624.

[8]Y.Tan and J.Yang,Phys.Rev.E 64(2001)056616.

[9]R.H.Goodman and R.Haberman,Phys.Rev.E 71(2005)056605.

[10]B.A.Malomed,Phys.Rev.A 43(1991)410.

[11]C.De Angelis and S.Wabnitz,Opt.Commun.125(1996)186.

[12]R.Kockaert and M.Haelterman,J.Opt.Soc.Am.B 16(1999)732.