A Few Discrete Lattice Systems and Their Hamiltonian Structures,Conservation Laws∗

Xiu-Rong Guo(郭秀荣), Yu-Feng Zhang(张玉峰), Xiang-Zhi Zhang(张祥芝),and Rong Yue(岳嵘)2College of Mathematics,China University of Mining and Technology,XuZhou 226,China

2Basic Courses,Shandong University of Science and Technology,Taian 171019,China

1 Introduction

Some interesting works for generating discrete integrable systems byr-matrix theory have been made great progresses.For example,Blaszak,et al.[1−4]introduced some Lie algebras consisting of shift operators to generate discrete integrable hierarchies whose Hamiltonian structures,recursive operators,and so on were obtained.These discrete systems extensively apply to mathematical physics,numerical analysis,statistical physics,and quantum physics.Qiao[5−6]utilized ther-matrix to get some discrete systems and discovered their algebraic-geometric solutions.As for some theories onr-matrices,we can refer to such the outstanding works appearing in Refs.[7–10].In the paper,we would like to apply three shift operators from a shift-operator Lie algebra to generate a few discrete integrable systems with 5-lattice fields whose Hamiltonian structures are obtained by making use Poisson tensors of an induced Lie–Poisson bracket.Such integrable systems can be reduced to the well-known Toda lattice system with a constraint.As we all know that the Toda lattice equation governs a system of unit masses connected by nonlinear springs whose restoring force is exponential.Obviously,some related results for the Toda lattice obtained in the paper implements the theory on discrete integrable systems.Next,with the help of Lax representations of the discrete integrable systems,we discover the recursion operators,which can be used to deducing Darboux transformations of the corresponding discrete integrable systems so that exact solutions could be generated.Finally,we apply a reduction of the shift operators presented in the paper to deduce a new discrete lattice system.Furthermore,we extend the reduced shift operator to obtain an expanding system with three lattice vector fields,and their Lax pairs,in finite conservation laws are obtained,respectively,which are new results compared with those consequences presented in Refs.[1–4].In addition,we specially point out that the method for generating Hamiltonian structures is different from that in Refs.[1–4],which adopts the expansion of gradient of Casimir functions not the Casimir functions themselves.This is a simple and eきcient way.

2 Recall Some Basic Facts onR-Matrix

To reach the consequences above,we brie fly recall some basic facts onr-matrix according to Refs.[1–4,8–10]:

De finition 1Letgbe a Lie algebra.A linear mappingr:g→gis called ther-matrix,if the induced bracket

is again a Lie bracket.

A suきcient condition forrto be anr-matrix is the Yang–Baxter equation(YB(α)):

whereαis some real number.

Assumegis an associative algebra with a Lie product[a,b]=ab−ba,andghas a non-degenerate,symmetric trace form tr:g→R.Then tr leads to an invariant metric ong:〈,〉:g×g→Rdefined by

which allows us to identitygwith its dualg∗.

De finition 2Assumegis a Lie algebra with Lie bracket[,].The induced Lie–Poisson bracket ong∗is the Poisson bracket{,}:C∞(g∗)×C∞(g∗)→C∞(g∗)presented by the formula

where dfis the differential off.

Based on Eqs.(1)and(2),it is possible to introduce different other brackets onC∞(g∗),[3]here we only list one of them as follows

which can be veri fied that Eq.(3)is a Poisson bracket.A Poisson tensor associated with Eq.(3)is defined by

Theorem[3]The Casimir functions of Lie–Poisson bracket(2)ong∼=g∗are in involution with respect to Eq.(3).The Hamiltonian flow related to a Casimir functionHis the Lax equation

Usually,the natural set of Casimir functiongis given by

In what follows,we again introduce how to get anrmatrix.In general,the Lie algebragcan be split into a direct sum of two of its proper subalgebras:g=g+⊕g−.Then the difference of the projection operators onto the subalgebras

satisfies YB(1).Hence Eq.(7)is anr-matrix.Thus,the Lax equation(5)can be written as

whereAk=P≥K(Lq).The variation ΔCqof the Casimir functionCqcan be determined by the following Novikov–Lax equation

where▽Cm(L)=hereEf(n)=f(n+1)E.

By using Eq.(7),Lax equation(8)can be written as

It has proved that the following shift operators

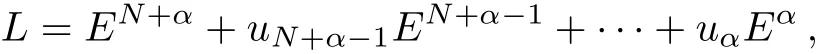
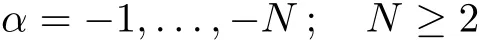
consist of a Lie algebra

The corresponding Lax equation presents in terms of Eq.(8):

Two possible reductions of Eq.(12)are as follows

which is a discrete Gelfand–Dikii analog.

In the next section,we shall introduce three shift operators from the Lie algebra(11)and make use of thermatrix and related theory stated above to generate a few discrete integrable systems as well as their Hamiltonian structures.

3 Discrete Integrable Systems and Hamiltonian Structures

Consider the following three shift operators

We shall applyLi(i=1,2,3)and Lax equation(12)as well as the Novikov–Lax equation(8)to produce discrete integrable systems.

3.1 Applications of L1,L2and L3

Whenq=1,one infers in terms of Eq.(8)that

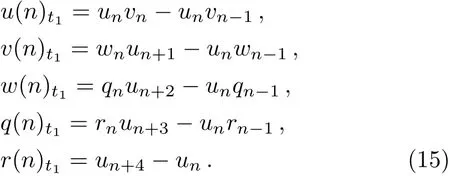
Whenr(n)=q(n)=0,w(n)=1,Eq.(15)reduces to the well-known Toda lattice system with the constraintun+4−un=0.

Whenq=2,we have

where

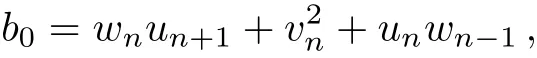
Thus,Lax equation

admits the discrete integrable system

Obviously,the discrete integrable system(17)looks complicated.Actually,it is a discrete expanding integrable model of Eq.(15).

As forL2,whenq=1,it is easy to see that

Lax equation

gives rise to the following discrete integrable system

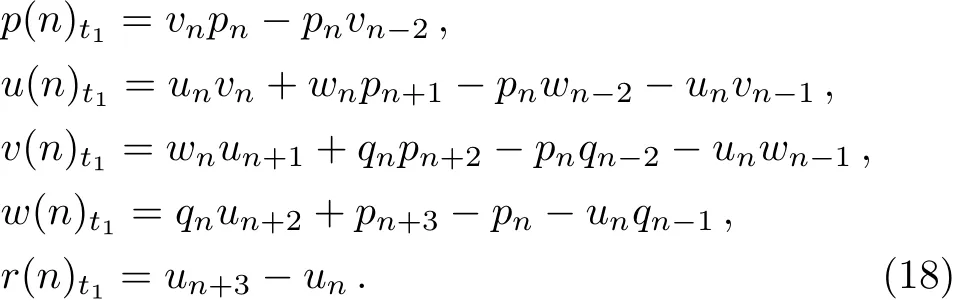
Whenq=2,3,...,we can apply Lax equations

to generate a series of discrete integrable systems.

Similar to the above discussions,whenq=1,Lax equation

leads to a discrete integrable system with 5-lattice vector fields:

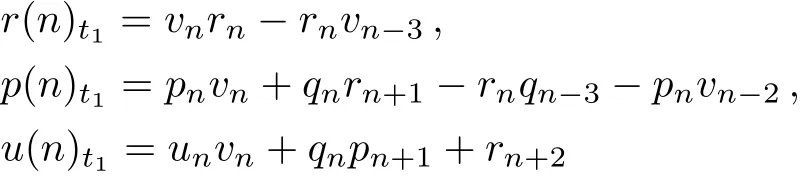
Whenq=2,3,...,Lax equation

could produce some new discrete integrable systems,here we omit them.

3.2 Hamiltonian Structures of the Discrete Systems(15)(18)and(19)

[1–4]adopt formula(6)to derive Hamiltonian structures of the discrete integrable systems obtained by Blaszak,et al.In the subsection,we apply the gradient dHof the Casimir functionHto deduce the Hamiltonian structures of the discrete integrable systems(15),(18),and(19).The formula for calculating the gradient dHis as follows

For the discrete integrable system(15),we suppose

It is easy to compute that

Thus,the discrete integrable system(15)can be written as by Eqs.(8)and(10):

where the Poisson tensor is denoted by

For the discrete integrable system(18),we assume that

It is easy to have that

Hence,

Therefore,the discrete integrable system(18)can be written as Hamiltonian structure

where

For the discrete integrable system(19),similar to the previous cases,let

One infers that

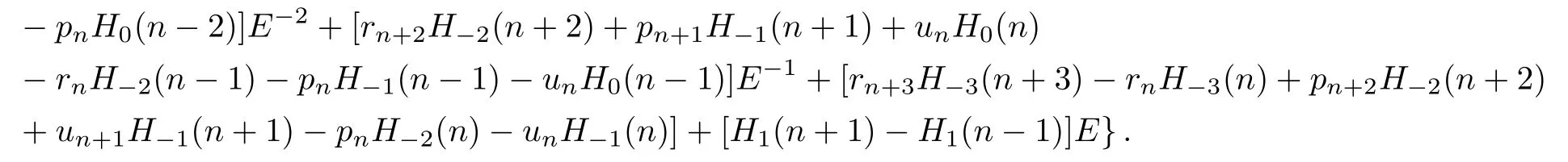
Therefore,the discrete integrable system(19)can be written as Hamiltonian form

where

4 Recursion Operators of Discrete Integrable Systems

Blaszak[4]once studied recursion operators of some continuous and discrete integrable system by various Lax equations.In the section,we follow his approach to seek for recursion operators of discrete integrable systems with multi-component Lattice-vector fields.For arbitrary element in Lie algebra(11),the corresponding Lax equation(8)can be written as

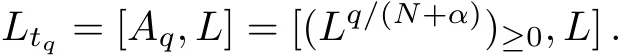
Then the operatorAm+N+αcan be expressed byAm:

where

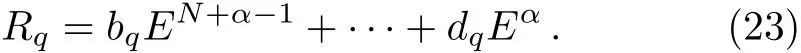
Thus,

As for the discrete integrable system(15),the corresponding shift operatorL1possessesN+α=4,α=−1,hence,N+α−1=3.From Eq.(23),we suppose

wherebi,q(i=−1,0,1,2,3)are to be determined.Hence,

where

After tedious calculations,we have

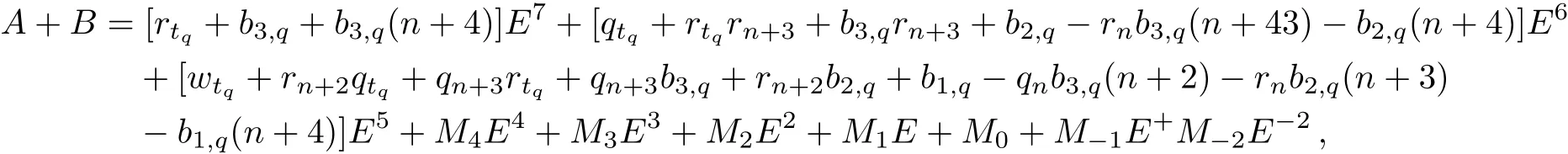
where

where operatoreis defined by

Equation(26)gives rise to the following recursion relations

Submitting Eq.(27)into Eq.(32),we could get the recursion operator Φ1satisfying

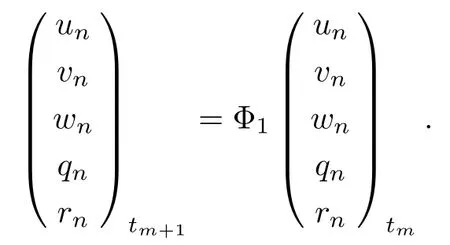
Because calculation of Φ1is tedious,we omit it now.In next setion,we shall present explicit recursive operators when discrete integrable systems contain less Latticevector fields.The recursion operator Φ2of the discrete integrable system(18)is similarly discussed as above,here we also omit it.As for the recursion operator Φ3of the discrete integrable system(19),we brie fly discover it as follows.

Set

wheream,bm,cm,dm,fmare to be determined.Starting

we can get that

where

Since

set that

then we have

where

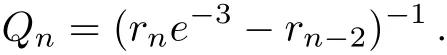
Substituting the above results into the following equations

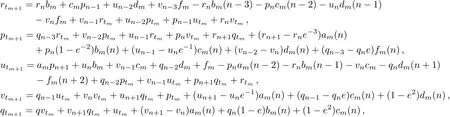
we obtain the recursion operator Φ3satisfying the relation

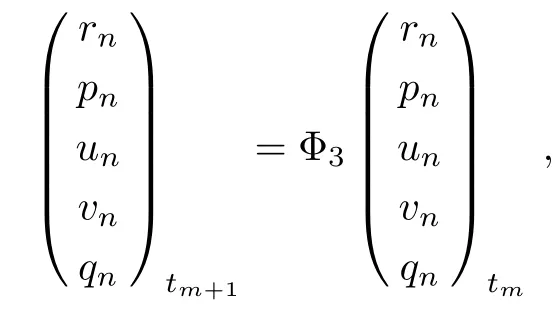
where

From Φ3,we find it has complicated expressing forms.

In order to recognize the structures of recursion operator of Φ1,we take a simpler form of the shift operatorL1as follows

By using Eq.(8),a discrete integrable system is obtained:[3]

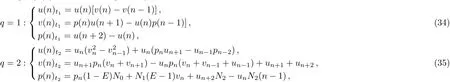
where

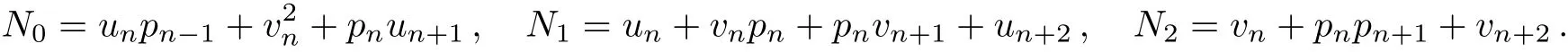
Denote by

where

It is easy to compute that

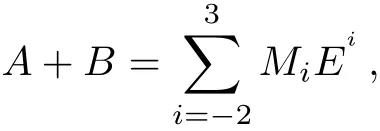
where

Thus,Lax equation

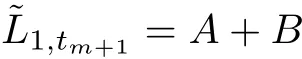
admits the following equations

Solving Eq.(36)yields

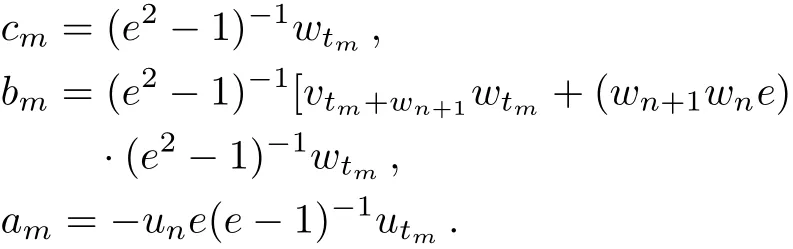
Substituting these results into Eq.(37),we have a recursion operator Φ of the discrete integrable system(34)which satisfies that

where

5 Conservation Laws of a Reduced Discrete Integrable Systems

Obviously,the shift operator(33)is an extended form of the following operator

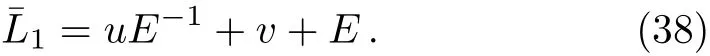
Hence,takingp(n)=0,system(34)should be reduced to the discrete integrable system which corresponds to Eq.(38)by applying Lax equation(8),which is just right well-known Toda lattice system.In what follows,we derive a generalized Toda lattice system from starting(38)and(8)as well as Eq.(9).

Setting

and solving the Novikov-Lax equation

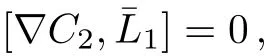
we have

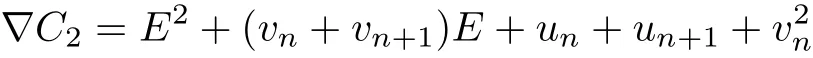
Inserting Eq.(39)into Lax equation

yields that

which is kind of reduction of Eq.(35).

At first,we seek for the Lax pair of Eq.(40).In terms of Eq.(38),we have

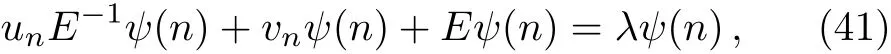
whereψ(n)is an arbitrary spectral function. TakingE−1ψ(n)=ψ1(n),ψ2(n)=ψ(n),then Eq.(41)can be written as

where

Since

it is easy to calculate that

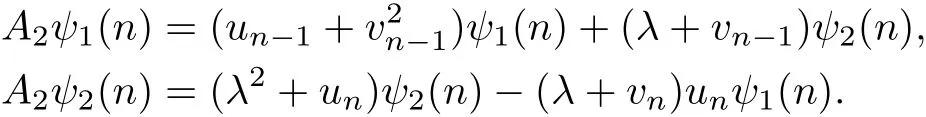
Thus,the time part of the Lax pair of discrete equation(40)is given by

Next,based on Eqs.(42)and(43),we generate in finite conservation laws of Eq.(40).

Taking Γn=ψn+1/ψn,then Eq.(42)can be written as

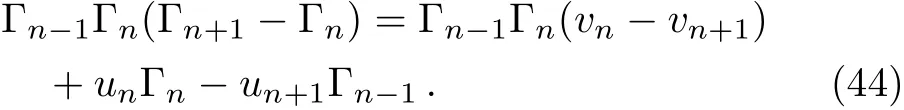
Assume

and substitute it into Eq.(44),we have

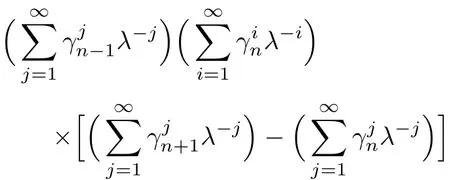
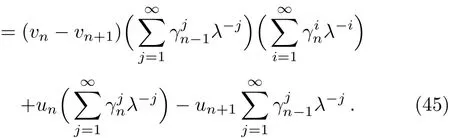
Comparing different coeきcients of power ofλyields as follows

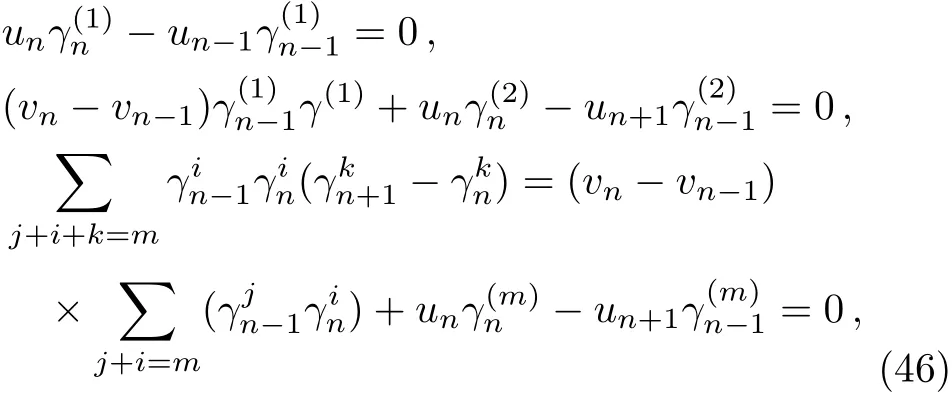
from which one infers that

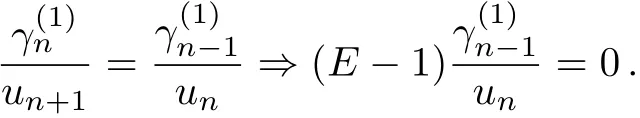
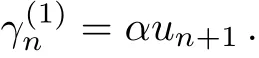
Equation(46)can be written as

βis a constant independent ofn.

Thus,we have

Besides,we know that

It is easy to find that

Hence,

which can be written as

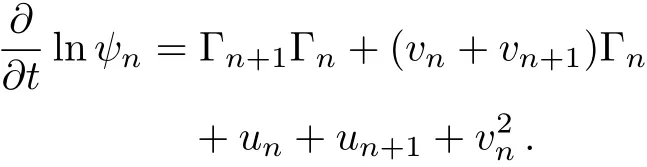
Therefore,Eq.(47)becomes

Since

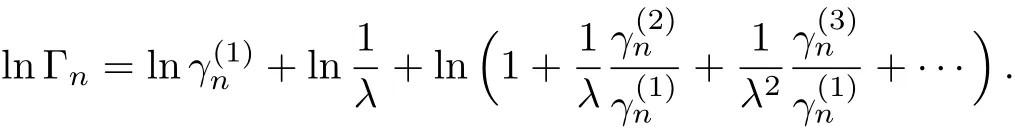
Thus,we see that

Note

then Eq.(49)has the following form

In terms of Eqs.(48)and(50),one finds that

which is the just right conservation laws.From Eq.(51),we see that

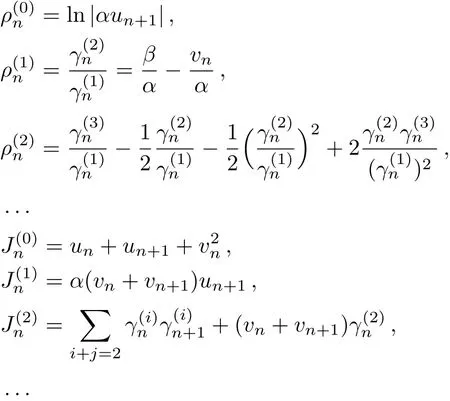
6 Conclusions

By introduced three-shift operators,we appliedrmatrix theory to have obtained a few discrete lattice systems,some of which are different from known results in Refs.[1–3].Specially,we made use of gradient operators of Casimir functions to deduce Hamiltonian structures of some results presented in the paper,which is an eきcient approach for generating Hamiltonian structures of discrete integrable systems,which modi fied the ways in Refs.[1–4].Concerning generation of discrete integrable hierarchies,Zhanget al.[11−14]has made some progressions which implement the results obtained in the paper,for example,paper[14]utilized continuous operators to have produced some new integrable systems and their Hamiltonian structures.However,there is a shortcoming in the paper which does not discuss exact solutions of discrete integrable equations.References[15–18]have proposed some approaches for generating exact solution of some integrable equations which have powerful enlightening roles.In the forthcoming days,we shall try to employ the ways in Refs.[15–18]to deduce some exact solutions of discrete equations.

[1]M.Blaszak and A.Szum,Rep.Math.Phys.44(1999)37.

[2]M.Blaszak and A.Szum,J.Math.Phys.42(2001)225.

[3]M.Blaszak and K.Marcimiak,J.Math.Phys.35(1994)4661.

[4]M.Blaszak,Rep.Math.Phys.48(2001)27.

[5]Z.J.Qiao,Rev.Math.Phys.13(2001)545.

[6]Z.J.Qiao,Chin.Sci.Bull.44(1999)114.

[7]M.A.Semenov-Tian-Shansky,Funct.Anal.Appl.17(1983)259.

[8]W.Oevel,Phys.Lett.A 186(1994)79.

[9]W.Oevel and O.Ragnisco,Physica A 161(1990)181.

[10]B.G.Konopelchenko and W.Oevel,Publ.RIMS Kyoto Univ.29(1993)581.

[11]Y.F.Zhang and Y.Wang,Adv.Differ.Equ-ny 2016(2016)313.

[12]Y.F.Zhang and X.J.Yang,J.Nonlinear Sci.Appl.9(2016)6126.

[13]Y.F.Zhang,et al.,Z.Naturforsch.A 72(2016)77.

[14]Y.F.Zhang,I.Muhammad,and C.Yue,Commun.Theor.Phys.(2016),accepted.

[15]Y.Y.Wang,Y.P.Zhang,and C.Q.Dai,Nonlinear Dyn.83(2016)1331.

[16]L.Q.Kong and C.Q.Dai,Nonlinear Dyn.81(2015)1553.

[17]C.Q.Dai,et al.,Nonlinear Dyn.86(2016)999.

[18]C.Q.Dai and Y.J.Xu,Appl.Math.Model.39(2015)7420.