Probabilistic Teleportation of an Arbitrary Two-Qubit State via Positive Operator-Valued Measurement with Multi Parties∗

Lei Shi(石磊),Jia-Hua Wei(魏家华),,2,† Yun-Xia Li(李云霞),Li-Hua Ma(马丽华),Yang Xue(薛阳),and Jun-Wen Luo(罗均文)

1Information and Navigation College,Air Force Engineering University,Xi’An 410073,China

2Department of Automatic Control,College of Mechatronics and Automation,National University of Defense Technology,Changsha 410073,China

1 Introduction

Quantum teleportation is a feasible technique for moving quantum states from senders to remote receivers via a quantum channel with the help of some classical information.It was first proposed by Bennettet al.[1]in 1993,and experimentally demonstrated by Bouwmeesteret al.[2]in 1997.Due to its potential applications in the realm of quantum communication,a growing number of theoretical and experimental progresses[3−18]have been made in this domain.Liet al.[5]proposed a scheme of probabilistic teleportation to transmit an unknown single-qubit using a non-maximally entangled state when the receiver introduced an auxiliary particle. Daiet al.[19−20]presented two protocols for probabilistically teleporting an arbitrary two-particle state from a sender to either one of two receivers via two partially entangled W states and by the combination of a non-maximally entangled GHZ state and an entangled W state,respectively.Meanwhile,some authors have generalized these methods to the case of the higher-dimensional quantum state.[7−10]Nevertheless,there are also many important and open subjects to be taken into account for quantum teleportation.

In most schemes[5−6,8−9,21−23]for probabilistic teleportation using partially entangled states as quantum channel,not only the senders need to perform some proper measurements,but also the receivers introduce one and more auxiliary particles and make some corresponding unitary transformations,corresponding to the information of the non-maximally entangled states.On the one hand,we would like to emphasize that the adopted measurements in the teleportation are usually projective measurements,and the post-measurement state of the senders’qubits is of little interest,with the main item of interest being the probabilities of the respective measurement outcomes.Thus,one can make use of Positive Operator-Valued Measurement(POVM)instead of usual projective measurements to study probabilistic teleportation.On the other hand,it is worth pointing out that the previous schemes[19−23]for transmitting two-qubit states are not valid in the situation that only the senders fully know the information of non-maximally entangled states to recover quantum states.As a matter of fact,some schemes[21−23]for probabilistic teleportation of an unknown two-qubit state via POVM had been proposed.Yanet al.[21]and Wanget al.[22]proposed two schemes of probabilistic teleportation of two-qubit states by using of POVM.Nevertheless,to our best knowledge,so far there are few papers exploring how to take advantages of POVM to realize the teleportation with multi-parties when the information of the partially entangled state is only available for the senders.The purpose of this paper is to present a novel scheme for probabilistic teleportation of an arbitrary unknown two-qubit quantum state by using of POVM and two partially entangled states with two senders and two receives.Futhermore,the concrete implementation processes of this scheme are elaborated,and the classical communication cost and the successful probability are calculated.

The rest of this paper are organized as follows:We will present a novel scheme for probabilistic teleportation of an arbitrary unknown two-qubit quantum state by using of POVM with multi-parties in Sec.2,and the correlative measurement operators for POVM are given in detail.In Sec.3,the concrete implementation processes of this scheme are elaborated.Moreover,the unitary transformations are given.The paper concludes with Sec.5.

2 Probabilistic Teleportation for an Arbitrary Unknown Two-Qubit State via POVM

In this sequel,a novel scheme for probabilistic teleportation of an arbitrary two-qubit state would be presented by using of POVM with two senders and two receivers.Suppose that the separate senders Alice and Clark want to transmit the following unknown two-qubit quantum state to the remote receivers Bob and David

where the complex numbersα,β,γandδsatisfy the normalization condition|α|2+|β|2+|γ|2+|δ|2=1.Without loss of generality,the entanglement channel is composed of two partially entangled two-particle states below

whereaandcare nonzero real coeきcients,banddare complex ones,and they satisfy|a|2+|b|2=1,|c|2+|d|2=1,|a|≥ |b|＞0 and|c|≥ |d|＞0,respectively.ParticlesAbelongs to Alice,particleCis in Clark’s possession,while the receivers Bob and David have particlesBandD,respectively.In the above case,the overall state of the six qubitsi,j,A,B,CandDis given by

Actually,our scheme needs to take advantage of POVM[25]with the measurement operatorsMk(i,A)andMl(j,C),here(k,l=0,1,2,3,4).

It is underlined that the aforementioned operators satisfy the completeness relationIf and only if the quantum channel is composed of two maximally entangled states,i.e.,the measurementsMk(i,A)andMl(j,C)would become the following Bellstate measurements

where the Bell states|ϕ±〉and|Ψ±〉are given by

Fig.1 Quantum circuit for probabilistic teleportation via POVM.Particle i and A are in the sender Alice’s possession,particles j and C belong to the sender Clark,while the receivers Bob and David have particles B and D,respectively.The box POVM denotes Positive Operator-Valued Measurement,given by Eqs.(5)and(6).The unitary operations UB are finished by Bob,and UDis implemented by David.The double wires carry classical bits,and the single wires carry qubits.Time proceeds from left to right.

The quantum circuit for probabilistic teleportation by suing of POVM is depicted in Fig.1.In order to reconstruct the original state,Alice performs the measurementsMk(i,A)on particlesiandA,and the measurementsMl(j,C)are implemented on particlesjandCby Clark.Then they inform Bob and David of the measurement results with the help of some classical information,respectively.Based on the POVM results of Alice and Clark,Bob and David perform the relevant unitary transformationsUBandUDon particlesBandD,respectively.Table 1 shows the POVM results on particles(i,j,A,C)and the unitary transformationUBandUD.

It is noting that the teleportation fails on the situation ofM4(i,A)orM4(j,C),otherwise the teleportation will be realized with the successful probability of|bd|2/4.It can be demonstrated that the teleportation is successfully obtained with the equal probability under the sixteen kinds of measurement results,shown as Table 1,hence the whole successful probability of quantum teleportation is

On the other hand,the classical communication plays an important role in quantum teleportation,and the total amount of classical communication required in our proposal is We would like to emphasize that the overall successful probability euqals to one and the classical communication cost is 4 bits,wheni.e.,the quantum channel is composed of two maximally entangled state.The results are in agreement with the overall successful probability and classical communication in Ref.[7].

Table 1 The POVM results and the unitary transformation UBand UD.

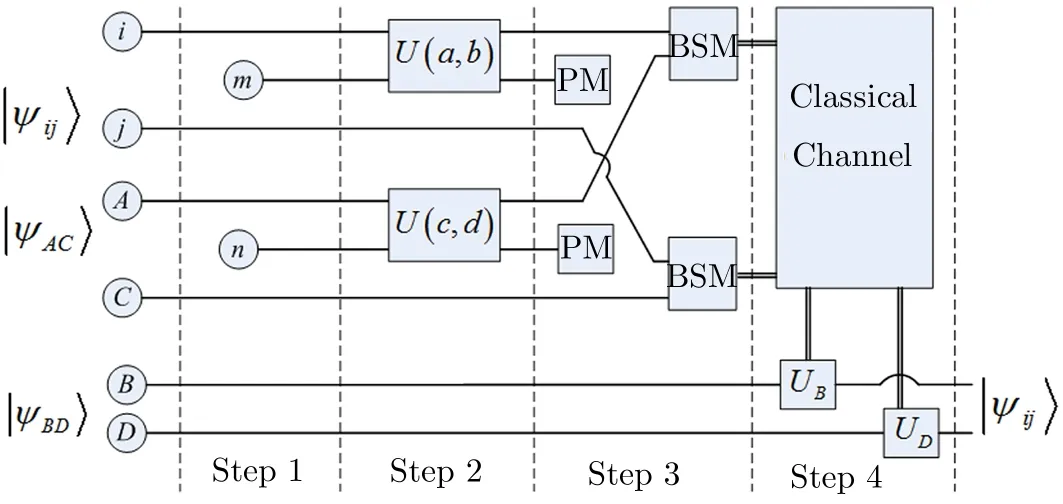
Fig.2 A sketch of the concrete processes for the novel probabilistic teleportation.The senders Alice and Clark introduce the auxiliary particles l and n,respectively.The box BSM denotes the Bell-state measurement,and the box PM is the projective measurement in the basis{|0〉,|1〉}.Alice performs the unitary operations U(a,b),Clark implements the gate U(c,d),while the receivers Bob and David complete the transformation USand UT,respectively.

3 Concrete Processes of This Novel Scheme

In reality,projective measurements together with unitary operations are suきcient to implement POVM with the aid of the introduction of auxiliary particles[24−25]Figure 2 presents the concrete processes for the novel probabilistic teleportation by using of POVM.Moreover,the detailed implementation procedures of our proposal are elaborated as follows

Step 1Alice and Clark introduce two auxiliary particlesmandnwith an initial state|0m0n〉,respectively,then the system could be written as

Step 2On particlesiandm,Alice performs a unitary transformationU(a,b),which takes the form of the following 2×2 matrix

Meantime,Bob performs a unitary operationU(c,d)on particlesjandn.Then we can express the system as

where the probability factorspt(t=1,2,3,4)are described as

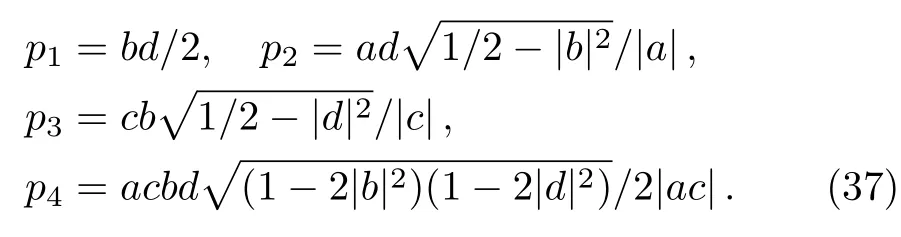
Step 3Alice measures the state of this auxiliary particlem,and completes the Bell-state measurements on particlesiandA,successively.Meanwhile,Clark performs the same measurements on particlesn,jandC.Subsequently,Alice and Clark inform Bob and David of the measurement results using a classical channel,respectively.Based on Eqs.(12)–(36),we can find that if particlemis|1m〉,particlesAandBwould collapse into|0A0B〉,which is not an entanglement state,thus the teleportation can not be performed.Similarly to particlem,particlesCandDwould become|0C0D〉when the state of particlenis|1n〉.Actually,we only need to explore how to realize the teleportation on the situation that the state of particlemis|0m〉and particlenis|0n〉,given by Eqs.(12)–(27).Namely,the teleportation could be realized successfully when particlesmandnare|0m0n〉with the probability of 16and the total probability is equal to one when quantum channel is composed of two maximally entangled states,i.e.,

Step 4In order to obtain the original state,Bob only needs to perform a unitary transformationUSon particleBbased on Alice’s measurement results,and David completes a relevant operationUTfor particleD.Table 2 indicates how to select the gatesUSandUTin terms of the measurements results of Alice and Clark.RemarksAccording to the aforementioned analyses,we would like to point out that:

Table 2 The unitary transformations UBand UD based on Alice’s and Clark’s measurements results.

(i)It should be underlined that one can use our scheme to carry out probabilistic teleportation when only the senders Alice and Clark know the partially entangled states.This is different from the former ones that the receivers Bob and David must have complete information of the entangled states.

(ii)Compared with the previous schemes[5−7,21−23]for probabilistic teleportation,an arbitrary unknown two-qubit quantum state from two senders Alice and Clark would be transmitted to two receivers Bob and David,instead of one sender and one receiver,hence this scheme could be used to probabilistic teleportation with multi-parties.

(iii)The classical communication cost of our present scheme equals to 4|bd|2,and the total successful probability is−4|bd|2log2(|bd|2/4).If and only ifi.e.,quantum channel is composed of two maximally entangled state,the classical communication cost and the overall successful probability equal to 1 and 4 bits,respectively.

4 Discussions and Conclusions

In summary,we put forward a novel scheme to probabilistically prepare an arbitrary unknown two-qubit state with the help of POVM.Moreover,the detailed realization procedures of this scheme are elaborated,the classical communication cost and the successful probability are calculated,respectively.In contrast to the previous schemes,[5−9,11,13−14,19−23]our current one has the following advantages.First,the novel proposal could be utilized to probabilistically transmit quantum states with two senders and two receives.Therefore,this scheme could enlarge the applied range of quantum communication with multi-parties.Second,one can make use of our proposal to perform the teleportation of two-qubit states when the information of the partially entangled states is only available for the senders,whereas the previous schemes are not feasible unless the receiver completely knows the partially entangled state.Third,the advantages of POVM can be used for probabilistic teleportation,and moreover,this idea can be generated to other quantum information systems,such as remote state preparation.Furthermore,we would like to point out that our novel scheme could be generalized to the teleportation of multi-qubit states by using of multi entangled states and POVM.From Refs.[14,16,24–25],one can find that all of these operations introduced for POVM could be realizable physically.Thus,from the point of the potential applications of the teleportaiton,we believe that our scheme will play an important role in expanding the field of quantum information processing.

[1]C.H.Bennett,G.Brassard,C.Grepeau,R.Jozsa,A.Peres,and W.K.Wootters,Phys.Rev.Lett.70(1993)1895.

[2]D.Bouwmeester,J.W.Pan,K.Mattle,M.Eibl,H.Weinfuter,and A.Zeilinger,Nature(London)390(1997)575.

[3]D.Boschi,S.Branca,F.D.Martini,L.Hardy,and S.Popescu,Phys.Rev.Lett.80(1998)1121.

[4]A.Karlsson and M.Bourennane,Phys.Rev.A 58(1998)4394.

[5]W.L.Li,C.F.Li,and G.C.Guo,Phys.Rev.A 61(2000)034301.

[6]H.Y.Dai,P.X.Chen,and C.Z.Li,Chin.Phys.12(2003)1354.

[7]G.Rigolin,Phys.Rev.A 71(2005)032303.

[8]H.Y.Dai,P.X.Chen,L.M.Liang,and C.Z.Li,Phys.Lett.A 355(2006)285.

[9]H.Y.Dai,M.Zhang,and C.Z.Li,Commun.Theor.Phys.49(2008)891.

[10]M.Al-Amri,J.Evers,and M.S.Zubairy,Phys.Rev.A 82(2010)022329.

[11]H.Y.Dai,M.Zhang,J.M.Chen,and C.Z.Li,Chin.Phys.B 20(2011)050310.

[13]M.Jiang and D.Y.Dong,Quantum Inf.Process.12(2012)237.

[14]J.H.Wei,H.Y.Dai,and M.Zhang,Commun.Theor.Phys.60(2013)651.

[15]X.H.Li and S.Ghose,Phys.Rev.A 90(2014)052305.

[16]J.H.Wei,H.Y.Dai,and M.Zhang,Quantum Inf.Process.13(2014)2115.

[17]X.H.Li and S.Ghose,Phys.Rev.A 91(2015)012320.

[18]J.Kim,J.Lee,S.W.Ji,H.Nha,P.M.Anisimov,and J.P.Dowling,Opt.Commun.337(2015)79.

[19]H.Y.Dai,P.X.Chen,and C.Z.Li,J.Opt.B 6(2004)106.

[20]H.Y.Dai,P.X.Chen,and C.Z.Li,Opt.Commun.231(2004)281.

[21]F.L.Yan and H.W.Ding,Chin.Phys.Lett.23(2006)17.

[22]Z.Y.Wang,D.Wang,J.Liu,and S.H.Shi,Commun.Theor.Phys.46(2006)859.

[23]X.B.Chen,N.Zhang,S.Lin,Q.Y.Wen,and F.C.Zhu,Opt.Commun.281(2008)2331.

[24]M.Zhang,H.Y.Dai,X.C.Zhu,X.W.Li,and D.W.Hu,Phys.Rev.A 73(2006)032101.

[25]M.A.Nielsen and I.L.Chuang,Quantum Computation and Quantum Information,Cambridge University Press,Cambridge(2000).