Accidental Degeneracies in N dimensions for Potential Class αr2d−2 − βrd−2via Asymptotic Iteration Method(AIM)

H.F.Kisoglu and Hakan CiftciDepartment of Basic Sciences,Faculty of Maritime,Mersin University,Mersin,Turkey

2Physics Department,Science Faculty,Gazi University,Ankara,Turkey

1 Introduction

In quantum mechanics,a microsystem is probed using many different mathematical methods.The energy eigenvalue equation of Hamiltonian of the system is solved for obtaining the energy eigenvalues and eigenfunctions.The potential function,i.e.type of interaction in the system,has a crucial role in this survey as it determines approaching way for the solution of the eigenvalue problem.

There are conventional methods can be performed such as WKB,perturbation theory,etc.for solving the energy eigenvalue eqution.[1−4]Alternatively,a method named as Asymptotic Iteration Method(AIM)[5−6]is widely used in recent years.The AIM can be utilized not only for obtaining the approximate(or numeric)solutions but also for exact and quasi-exact solvable problems.[7−12]It can be also used in the scope of perturbation theory and has some advantages over the familiar perturbation expansion because it does not require unperturbed(stable states)Hamiltonian to calculate the coeきcients of the series expansion.[8,13−17]

In this study,we tackle the potential class given asαr2d−2−βrd−2whereαandβare coupling constants(α,β＞0)andd∈＞0.[18−20]This potential class was arised out firstly by Khare’s study.[19−20]In particular,it corresponds the Coulomb and the oscillator potential ford=1 andd=2 respectively,and Hamiltonian of the system has exact energy eigenvalues.Khare showed that there are local accidental degenerecies and bound states forE=0,for the Schrödinger’s equation with this potential class in spherical coordinates.In 2012,Bera[18]rederived the exact energy eigenvalues of Schrödinger equation ford=1 andd=2,by using Nikiforov–Uvarov(NU)method[21]in two dimensions.He also reconsiders the problem using NU method inNdimensions(N≥2)forE=0.

We use AIM to obtain approximate energy eigenvalues of Schrödinger equation for this potential class inN-dimensional euclidean space ford=3 andd=4.The eigenvalues are also obtained by using the perturbation theory in the view of the AIM to compare with those as obtained approximately.

According to organization of the paper,we give a brief introduction about the AIM and perform it to obtain the approximate energy eigenvalues in Secs.2 and 3,respectively.In Sec.4,we summarize the perturbation theory in the frame of AIM and obtain the perturbative eigenvalues by performing the AIM.

2 Outline of Asymptotic Iteration Method(AIM)

The AIM was announced in Ref.[5]for figuring out the second-order linear differential equations in a form of

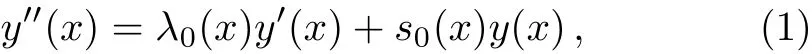
whereλ0(x)ands0(x)have continuous derivatives in the designated domain of the problem.

TheoremDifferential equation in such a form of(1)has a general solution as follows

if the following aspect exists

forn＞0 wheresnandλngiven as follows

under the assumption thatnis large enough.The AIM can be used for solving Schrödinger equation for a physical system in quantum mechanics.The(unkown)Enenergy eigenvalues of Schrödinger equation are obtained from

termination condition achieved by the means of(3).

Table 1 Some of numeric energy eigenvalues Enlfor N=3 to 10,obtained by directly application of the AIM,for d=3 and d=4(β =2,α =0.3).The subscript represents the number of iteration.

The eigenvalue equation,given in Eq.(1),can be solved exactly ifδn(x,E)=0 is satisfied for allxvalues in the defined domain of the problem.Otherwise,a convenient valuex≡x0should be specified for starting the AIM.One can obtain thex0from the zeros of theλ0.[7,22]

3 Formulation of the Problem

In this study,we use AIM to tackle the potential class given as

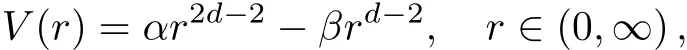
inNdimensions whereα,βare coupling constants(α,β＞0)andd∈＞0.

The radial Schrödinger equation inN-dimensions for such a potential class is written as(ħ =m=1)

where Ψ(r)=r(N−1)/2R(r)andη=l+(N− 3)/2(N≥ 2,N∈Z),l=0,1,2,...is angular momentum quantum number.For polar and spherical coordinatesNis taken asN=2 andN=3,respectively.The cases forN＞3 represent hyperspherical coordinates.According to the boundary conditions,the wave function(eigenfunction)Ψ(r)can be assumed as

One can obtain the following differential equation substituting(7)into(6)

If we define a new variable such asx=(2α)1/2dr,the following equation is got

whereω=2E/(2α)1/dandγ=This equation is in appropriate form for initiating the AIM with the functions

with regarding to(9).

3.1 Direct Application of AIM to the Problem

In direct application of the AIM,arbitrary potential parametersd,αandβare used.Furthermore,a suitablex=x0initial value is needed to initiate the AIM iterations.One can find an adequate value asx0=(1+η)1/dfrom the zeros ofλ0=0.[7]SomeEnlenergy eigenvalues forN=3 to 10 dimensions,obtained by direct application of the AIM,are reported in Table 1 ford=3 andd=4.

As is seen from the eigenvalues in Table 1,for a givend,there are accidental degeneracies coincide with the following rule

wherel2=l1+1 andN′=N+2.According to this outcome,we can say that the energy spectrum can be constructed if a few eigenvalue is known.

4 Perturbation Method of AIM

The AIM can also be used for obtaining the perturbative eigenvalues in the scope of perturbation theory.We refer the readers to the original publication[13]for a detailed introduction and applications.Presume the potential of the system is as follows

whereV0(x)is the potential of the stable(unperturbed)states whileVp(x)is unstable(perturbed)states’potential.ρis the perturbation constant(ρ＜1).So,the Schrödinger equation for the system in one dimension is written as

In perturbation theory,the eigenvalues of(13)Enis written as

which is in suitable form for the AIM.

If we expand the termination conditionδn(x,ρ,E)=0 aboutρ=0,we get

where

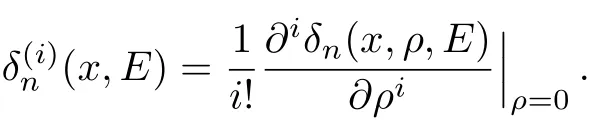
Using Eqs.(5)and(16),we get

condition for eachi.Thei-th order correction,,toEncan be obtained by solving the equationforE,in the perturbation calculations of AIM.Similar procedure is followed to attain the eigenfunctions.Theith order correction,,to the eigenfunctionis achieved with no necessity to the following stable state’s eigenfunction

whereαn(z,ρ) ≡sn(z,ρ)/λn(z,ρ).This is one of the alluring specialities of AIM.If theαn(z,ρ)in Eq.(18)is written in the form of perturbation expansion

as done for the eigenvalues in Eq.(14),thenfn(x)reads

where

Therefore,thei-th order correctiontofn(x)in Eq.(20)is as follows

4.1 Perturbation Method of AIM for the Problem

We have the proper differential equation,obtained in the previous section,as follows

for which the AIM can be applied.The parametersγandωare given asrespectively.We find the perturbative energy eigenvalues inN=5 andN=7 dimensions in the frame of AIM ford=3,in this section.

We can write the parameterγas perturbation expansion as follows:

whereωhas been chosen as perturbation expansion parameter,differently from thestandard Rayleigh–Schrödinger perturbation series.[23]The general form of the zeroth order correctionγ(0)toγis obtained by means of

as mentioned previously.We have solved this equation forγ(0)by taking the initialxvalue asx0=(1+η)1/d.Numeric results ofγ(0)for the first six energy levels inN=5 andN=7 dimensions are given in Table 2.

So,theγ(0)can be generalized as

regarding to the results given in Table 2.

Numeric values for the correctionsγ(1),γ(2),γ(3),...have to be found for each different value of eithernorlquantum numbers since theγ(0)n,ldepends on bothnandlfor a givenN.We report the numeric values forγ(1),γ(2),γ(3),γ(4),γ(5),obtained by using AIM takingx0=(1+η)1/d,in Table 3,forn=1,2,3 andl=0,1,2.The comparison of the perturbative energy eigenvaluesEp,obtained numericaly by using AIM,with directly calculated onesEdirect(see in Table 1)is reported in Table 4.The initialxvalue isx0=(1+η)1/dfor both pertubative and directly calculated energy eigenvalues.

So,existence of the accidental degeneracies such as Eq.(11)is corroborated by perturbation calculations of the AIM,according to Table 4.The eigenvaluesEpare also compatible with the ones obtained as directly.

Table 2 γ(0)zeroth order correction to γ in N=5 and N=7 dimensions for d=3.

Table 3 The numeric values for the corrections γ(1),γ(2),γ(3),γ(4),γ(5)to perturbation expansion of γ for n=1,2,3 and l=0,1,2.The parameter d has been taken as d=3 for the perturbation calculations.

Table 4 The comparison of the perturbative energy eigenvalues Ep,obtained numericaly by using AIM,with directly calculated ones Edirectseen in Table 1.E12has not been calculated for Edirect.

5 Conclusion

We have used AIM[5−6]to obtain approximate energy eigenvalues of Schrödinger equation for the potential classαr2d−2−βrd−2inN-dimensional euclidean space ford=3 andd=4(N≥ 2).The parametersαandβare coupling constants(α,β＞0)andd∈＞0.[18]

For this purpose,we have tackled the higher values ofdsuch asd=3 andd=4,and arbitrary potential parameters.The eigenvalues are not in exact form for the valuesd=3 andd=4 whereas the eigenvalue equation has exact solutions ford=1 andd=2,which represent Coulomb and harmonic oscillator potential respectively.Thus,Eenergy eigenvalues can be obtained numerically by directly application of the AIM.The initial value,which is necessary for starting the AIM iterations in such a calculation,has been found from the zeros ofλ0=0.According to the results,for a given value ofd,there are accidental degeneracies such aswherel2=l1+1 andN′=N+2.Such degeneracies can be illuminated by Eq.(24).There are two different(n,l,N)configurations for a given value ofin conformity with this equation.For instance,there is degeneracy such asfor the both energy levels.The numeric values of the corrections to perturbation expansion ofγare already the same for the energy levels which give degeneracy(see in Table 3).So,onlyn,landNplay roles on the degeneracies while the parametersαandβcan change just the numeric values of energy levels.We can say that the energy spectrum can be constructed if a few eigenvalue is known,with regarding to this outcome.

AIM can also be used in the scope of the perturbation theory.[6]In standard perturbation theory,the eigenfunctions of unperturbed Hamiltonian(solvable part)is needed for obtaining the coeきcients of the perturbation expansion.Furthermore,obtaining the coeきcients for the higher corrections to either energy eigenvalues or eigenfunctions is big challenge.The fascinating feature of the AIM is that the coeきcients of the perturbation expansion can be obtained without the need of the eigenfunctions of unperturbed Hamiltonian.In this study,we have also obtained the perturbative energy eigenvalues using the AIM,for arbitrary values of the potential parameters.For these calculations,the parameterω(see in Eq.(9))has been taken as perturbation parameter,differently from the standard Rayleigh–Schrödinger perturbation series.[23]According to the results,it is seen that the first-six corrections to perturbation expansion of the parameterγ(see in Eqs.(9)and(22))converge fastly.Furthermore,existence of the accidental degeneracies,seen in directly application of AIM,are corroborated by perturbation calculations in the view of AIM.There is,also,consistency between the perturbative eigenvalues and the eigenvalues obtained by directly application of the AIM.

[1]D.J.Griきths,Introduction to Quantum Mechanics,Upper Saddle River,New Jersey(1995)pp.221–323.

[2]L.D.Landau and E.M.Lifshitz,Quantum Mechanics Non-relativistic Theory,Long Island City,New York(1965)pp.50–75.

[3]B.Karaoglu,Kuantum Mekaniˇgine Giri¸s,Istanbul(1998)pp.150–151.

[4]B.Karaoglu,Kuantum Mekaniˇgine Giri¸s,Istanbul(1998)pp.137–142.

[5]H.Ciftci,R.L.Hall,and N.Saad,J.Phys.A:Math.Gen.36(2003)11807.

[6]H.Ciftci,R.L.Hall,and N.Saad,J.Phys.A:Math.Gen.38(2005)1147.

[7]H.Ciftci,R.L.Hall,and N.Saad,Cent.Eur.J.Phys.11(2013)37.

[8]H.Ciftci and H.F.Kisoglu,Chin.Phys.B 25(2016)030201.

[9]M.Chabab,A.El Batoul,and M.Oulne,Zeitschrift für Naturforschung A 71(2016)59.

[10]A.Demic,V.Milanovic,et al.,Mod.Phys.Lett.B 30(2016)1650003.

[11]N.Benchiheub,Y.Kasri,and A.Kahoul,Canadian J.Phys.93(2015)1486.

[12]A.V.Turbiner,J.Phys.A:Math.Gen.45(2012)025203.

[13]H.Ciftci,R.L.Hall,and N.Saad,Phys.Lett.A 340(2005)388.

[14]C.A.Onate and J.O.A.Idiodi,Chin.J.Phys.53(2015)120001.

[15]C.Y.Zhang,S.J.Zhang,and B.Wang,Nuc.Phys.B 899(2015)37.

[16]K.S.Alsadi,J.Nanoelectron.Optoelectron.10(2015)683.

[17]N.Kumaresan,M.Z.M.Kamali,and K.Ratnavelu,Chin.J.Phys.53(2015)080401.

[18]P.K.Bera,Pramana J.Phys.78(2012)667.

[19]A.Khare,Lett.Math.Phys.5(1981)539.

[20]A.Khare,J.Math.Phys.24(1983)867.

[21]A.F.Nikiforov and V.B.Uvarov,Special Functions of Mathematical Physics,Birkhauser,Basel(1988).

[22]M.Aygun,O.Bayrak,and I.Bostosun,J.Phys.B:At.Mol.Opt.Phys.40(2007)537.

[23]F.M.Fernandez and H.Ciftci,Phys.Lett.A 359(2006)272.