Equal-Time and Equal-Space Poisson Brackets of the N-Component Coupled NLS Equation∗

Ru-Guang Zhou(周汝光), Pei-Yao Li(李佩瑶), and Yuan Gao(高媛)

School of Mathematics and Statistics,Jiangsu Normal University,Xuzhou 221116,China

1 Introduction

It is well-known that Hamiltonia n structures are essential elementary properties for in finite-dimensional integrable systems.[1−2]In particular,for the(1+1)-dimensional integrable nonlinear systems with variablesxandt,the existence of bi-Hamiltonian structures is one of the most characteristic features.Indeed,the compatible equal-time or independent of temporal variabletHamiltonian operator pair may directly generate in finitely many commuting symmetries and constants of motion being in involution.

Recently Caudrelier and collaborators discovered that the nonlinear Schrödinger(NLS)equation has an equivalent Hamiltonian description of two variablesxandtby constructing two Poisson brackets,one for each spacetime coordinate.[3−4]The Poisson bracket corresponding to the space coordinate,in which time variabletis fixed,is the usual one describing the time evolution of the system;while the Poisson bracket corresponding to the time coordinate is new one.Furthermore,Caudrelieret al.showed that the two spectral matrices of Lax pair of the NLS equation satisfy the same form of ultralocal Poisson algebra(up to a sign)characterized by anr-matrix structure and the coexistence of two brackets is totally compatible with the usual properties of the NLS model,like the existence of an in finite number of conversed quantities.Hence,different from that in the bi-Hamiltonian theory,the variablesxandthave an equal position in this setting.In addition,as an application,the equal-space bracket has been used to reinterpret the defect Lagrangian as a generating function of canonical transformation in the NLS equation with defects.[3]

In the present paper we would like to extend the study to the integrableN-component coupled NLS equation[5]

which has broad applications in physical problems,[5−10]whereε= ±1,qj=qj(x,t)(1≤j≤N)are complex fields,and the superscript star denotes the complex conjugate.The equation withN=1 is nothing but the well-known NLS equation and the equation withN=2 is the Manakov equation.[6]AsN≥2 the equation has not only many of integrable properties similar to the NLS equation but also various interesting properties of their own.[11−18]

The paper is organized as follows.In Sec.2,two Poisson brackets for Eq.(1)are constructed.In Sec.3,rmatrix formations of the spectral matricesU,Vare given.We end with some conclusions and remarks in Sec.4.

2 Equal-Time and Equal-Space Poisson Brackets

The integrableN-component coupled NLS equation(1)can be derived from a variational principle.Actually,equation(1)is equivalent to the following Euler–Lagrange equation=0,1≤j≤N,where the Lagrangian density is

Following Ref.[4],we use Legendre transformation to construct the equal-time Poisson brackets which does not depend on time variable but only on the space variables.For convenience,let us denoteϕ1j=qj,ϕ2j=q∗j(1≤j≤N).Then the Lagrangian density may be written as

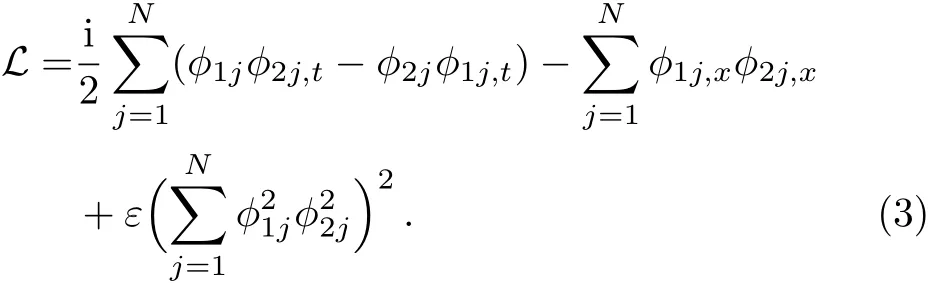
The usual canonical conjugate toϕ1j,ϕ2jare defined by

which means that Π1j,Π2j(1 ≤j≤N)have been constrained to the subspace spanning by fields:ϕ1j,ϕ2j(1 ≤j≤N).We have to modify the canonical Poisson brackets

to the Dirac bracket to keep the 2Nconstraints:

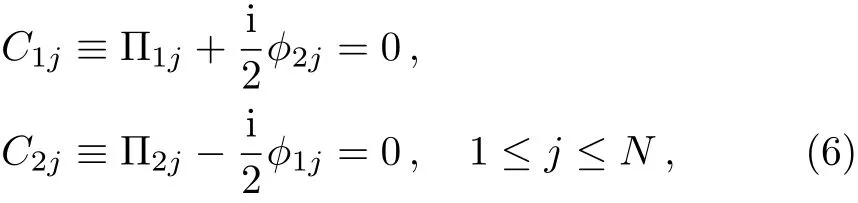
whereδ(x−y)is Diracδ-function.

From Eq.(5)we obtain

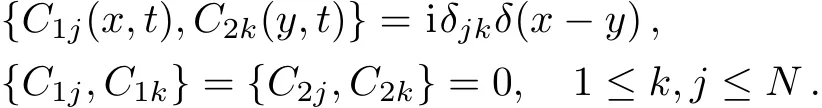
Therefore,the constraints(6)are second class and the Dirac bracket is defined by[19]After some algebra,we obtain the following fundamental Dirac brackets:

whereδjkis Kronecker delta which is 1 ifj=k,and 0 otherwise.

Finally,in terms of the original fieldsqj,q∗j(1≤j≤N),we obtain an equal-time Poisson bracket

wheretmay be understood as a fixed parameter.Equation(1)can be written as the following equal-time Hamiltonian form:

where the Hamiltonian is

with the equal-time Hamiltonian density

by the standard Legendre transformation.

Next we are going to construct equal-space Poisson brackets for Eq.(1).Again starting from the Lagrangian density(2),we choose 2Nindependent fieldsϕ1j,ϕ2j(1≤j≤N)and thus the corresponding canonical conjugate momentums are

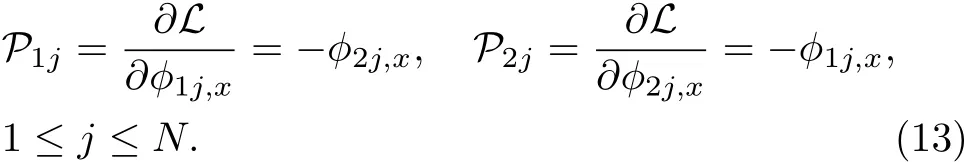
Therefore the phase space possesses 4Nfields:ϕ1j,ϕ2j,ϕ1j,x,ϕ2j,x(1 ≤j≤N)or in terms of the original fields:(1≤j≤N).

The equal-space Poisson brackets are

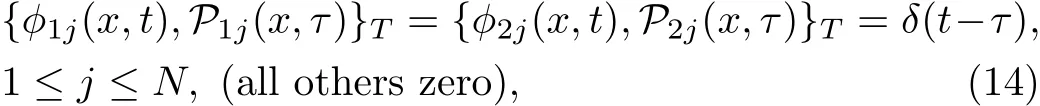
or,in terms of the original fields,

Equation(1)can be written as the following equalspace Hamiltonian form,

where the Hamiltonian is

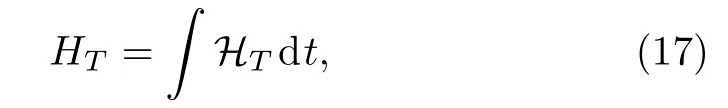
with the equal-space Hamiltonian density

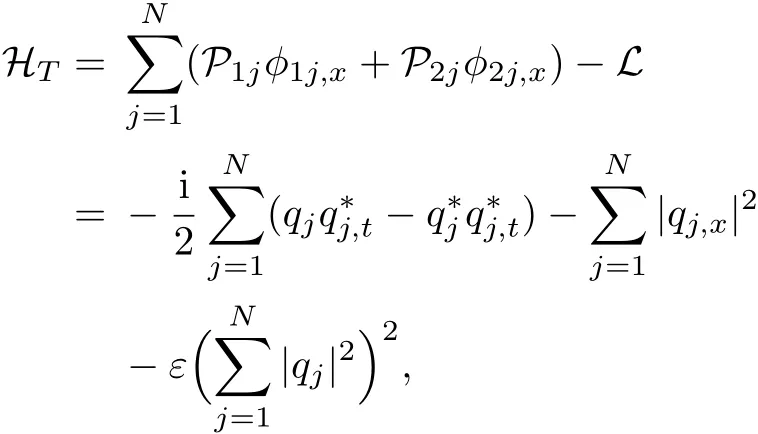
by Legendre transform.

3 Classicalr-matrix Formulations

By direct calculations,we know that Eq.(1)is equivalent to the zero curvature representation

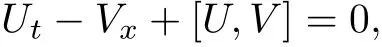
which is the compatibility condition of spectral problems or Lax pair

where

whereINis theN×Nidentity matrix,Q=(q1,...,qN)is anN-component row vector,and the superscript†denotes the Hermitian,i.e.complex conjugate transpose.

With direct calculations,we can obtain the following proposition.

Proposition 1Equipped with the canonical Poisson bracket{,}Sand{,}T,matricesU(x,t,λ)andV(x,t,λ)satisfy the following ultralocal Poisson algebras[1]

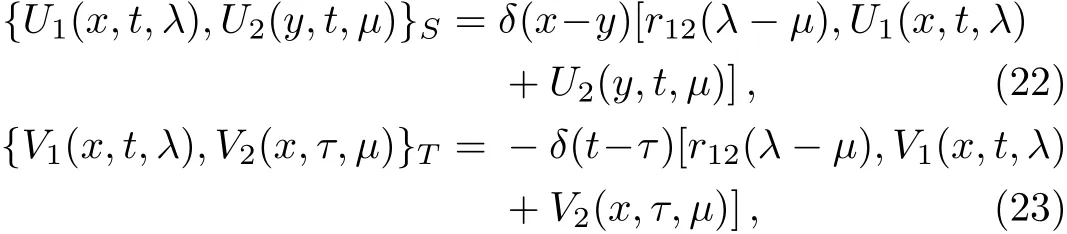
respectively,where we have used the notation

and

andeijis(N+1)×(N+1)matrix having 1 in the(i,j)-th position and zeros elsewhere.

RemarkSince the fields:q1,...,qNand corresponding momentum fields:in the equal-time case do not depend on the derivatives with respect to time parametert,we may exchange the positionsqj(1≤j≤N)andand define the following equal-time Poisson brackets:

Then equation(1)can be written as the following equaltime Hamiltonian form:

Obviously,under the equal-time bracketUenjoys the completely samer-matrix formulation toVwith respect to{,}T.

4 Conclusions and Remarks

In summary,we have constructed equal-time Poisson bracketand equal-space Poisson bracket{,}Tfor the integrableN-component coupled NLS equation(1)and shown that the spectral matrices share the samer-matrix algebras with respect to corresponding Poisson brackets.It is interesting to find applications of these results and generalize them to other soliton equations.

[1]L.D.Faddeev and L.A.Takhtajan,Hamiltonian Methods in the Theory of Solitons,Springer-Verlag,Berlin,Heidelberg,New York(1987).

[2]F.Magri,J.Math.Phys.19(1978)1156.

[3]V.Caudrelier and A.Kundu,J.High Energy Phys.02(2015)088.

[4]J.Avan,V.Caudrelier,A.Doikou,and A.Kundu,Nucl.Phys.B 902(2016)415.

[5]M.J.Ablowitz,B.Prinari,and A.D.Trubatch,Discrete and Continuous Nonlinear Schrödinger Systems,Cambridge University Press,Cambridge(2004).

[6]S.V.Manakov,Sov.Phys.JETP 38(1974)248.

[7]S.G.Evanglidis,L.F.Mollenauer,J.P.Gordon,and N.S.Bergano,J.Lightwave Tech.10(1992)28.

[8]L.F.Mollenauer,S.G.Evangelides,and J.P.Gordon,J.Lightwave Technol.9(1991)362.

[9]A.Hasegawa and Y.Kodama,Solitons in Optical Communications,Clarendon Press,Oxford(1995).

[10]Y.Kodama,A.Maruta,and S.Wabnitz,Opt.Lett.21(1996)1815.

[11]R.Radhakrishnan and M.Lakshmanan,J.Phys.A 28(1995)2683.

[12]A.P.Sheppard and Y.S.Kivshar,Phys.Rev.E 55(1997)4773.

[13]M.Vijayajayanthi,T.Kanna,and M.Lakshmanan,Phys.Rev.A 77(2008)013820.

[14]D.S.Wang,D.Zhang,and J.Yang,J.Math.Phys.51(2010)023510.

[15]Y.Ohta,D.S.Wang,and J.Yang,Stud.Appl.Math.127(2011)345.

[16]B.Guo and L.Ling,Chin.Phys.Lett.28(2011)110202.

[17]F.Baronio,A.Degasperis,M.Conforti,and S.Wabnitz,Phys.Rev.Lett.109(2012)044102.

[18]L.C.Zhao and J.Liu,Phys.Rev.E 87(2013)013201.

[19]P.A.M.Dirac,Can.J.Math.2(1950)129.