一种基于全局K-均值聚类的改进算法
2018-01-22李燕梅
李燕梅
(滇西科技师范学院,云南 临沧 677000)
1 引言
K-均值聚类算法通过迭代算法来解决实际应用中出现的聚类问题,并得出聚类误差的最优解,被广泛应用于聚类误差问题中。K-均值聚类算法采用随机的方式选择K个对象作为初始聚类中心,通过迭代算法降低聚类误差以达到改变聚类中心的目的,属于一种基于中心点的基础聚类算法。K-均值聚类算法的弊端在于选取初始聚类中心点相对慎重,进而影响了算法的效率。为得到K-均值聚类算法中聚类误差的近似最优解,需要合理安全初始聚类中心点的位置,确保每个聚类中心点之间存有差异。针对K-均值聚类算法面临的问题,专家学者不断深入研究,以期通过新型算法达到全局最优化的目的。但目前采取遗传算法、模拟算法等技术来解决该问题还存在一定的漏洞,适用性不强,导致认可度不高。因此,在解决实际问题中使用度最高的聚类算法还是K-均值聚类算法。本文提出基于K-中心点算法的改进思想,将其作为全局K-均值聚类算法的初始聚类中心,最后实现聚类时间短、鲁棒性强的目标。
2 K-均值聚类算法
K-均值聚类算法用于解决数据聚类问题,由麦克奎因首次提出。K-均值聚类算法具有算法简单、计算速度快的优势,广泛应用于工业、科技等领域。K-均值聚类算法处理了含有n个数据点集合如X={x1,x2,…,xn}中需要划分出以K为对象的Cj类簇问题,其中j=1,2,…k。K-均值聚类算法的步骤为:随机选取K个对象作为初始聚类中心,然后计算每个数据点与各个聚类中心之间的距离,并将数据点划分至距离最近的聚类中心内,以此形成K个初始聚类。对初始聚类中心根据聚类中现有的数据点重新计算,采用迭代算法进行划分,当聚类中心数值不再变化时,说明所有K数据对象已全部划分完毕,进而进行聚类准则函数收敛,如若数值还处于变化,则需要继续采用迭代算法划分,直至成功。K-均值聚类算法需要注意使用迭代算法时是对全部数据点进行分配,没有进入聚类中心的数据点在下次迭代过程中仍参与分配。当聚类中心不再变化后,说明聚类准则函数收敛完毕,K-均值聚类算法结束。
3 全局K-均值聚类算法
全局K-均值聚类算法是给定含有n个数据点集合如X={x1,x2,…,xn},以期将其划分为以K为对象的Cj类簇问题,其中j=1,2,…k,全局K-均值聚类算法具有全局最优算法的优势,无须依托于初始因素,提高了算法的确定性。全局K-均值聚类算法中的局域搜索程序采用K-均值聚类算法,全局K-均值聚类算法采用最优化方式在算法运行各个阶段添加新的聚类中心,聚类中心的初始值也不再随机选取。
针对实际应用环节中出现的K个簇聚类问题,全局K-均值聚类算法的步骤如下:将簇中心的最优位置确定为数据集的质心以此解决一个簇的聚类问题,以此类推,解决n个簇的聚类问题是执行n次全局K-均值聚类算法,明确簇的中心初始位置即可。当K-1为第一个聚类中心的最优解位置时,将x数据点作为第二个簇的初始聚类中心,i=1,2,...,n,运用全局K-均值聚类算法解决n次聚类问题后,得出K-2时的聚类问题解决方法为最优解。由此可知,使用全局K-均值聚类算法时,当我们得出(K-1)聚类问题的解决方法时,可以采用类似步骤解决K-均值聚类算法的问题。针对n次对应以K为对象的类簇问题,执行K-均值聚类算法,明确初始簇聚类中心,得出聚类问题的最优解。基于全局K-均值聚类算法的步骤,最终可以得出K个聚类问题的解决方式,当聚类数目小于K的聚类问题也可采用同类方式予以解决。
全局K-均值聚类算法的优势在于确定类聚中心数目,为充分发挥出此优势,需要有效解决各种簇数目的聚类问题,基于合理的准则来确定K值,不再随机选择K对象。因此,应用全局K-均值聚类算法可以排除初始类中心点对聚类算法结果造成的不良影响。但由于全局K-均值聚类算法中的全部K值都需要执行K均值算法,计算任务量大,所以多数使用者关心全局K-均值聚类算法应用是否过于复杂,因此在后续应用过程中改进该算法具有重要的作用。
4 基于全局K-均值聚类算法的改进
本文研究一种基于全局K-均值聚类算法的改进,首先需要对全局K-均值聚类算法进行有效掌握。其将K个聚类中心的问题转化为从局域搜索初始状态入手。当K=1时,增加一个聚类中心,需要用迭代算法求出K的聚类答案。全局K-均值聚类算法将K-1聚类质心作为默认样本,将K-1的前一个聚类中心作为K-均值聚类算法的最佳初始位置,通过反复运行全局K-均值聚类算法来确定最佳的初始中心。

图1 算法流程图
本文基于全局K-均值聚类算法的算法思想,提出新的初始化方法,将K中心为初始中心的思想融入全局K-均值聚类算法中,来确定下一个聚类中心的初始中心,形成一种新型改进方法。改进后的全局K-均值聚类算法需要针对密集的样本,找到距离现有簇中心较远的簇作为样本,并算出其最优初始中心,这样有利于避免现有簇中心点的干扰,也可以弥补全局K-均值聚类算法计算量较大的弊端。改进后的全局K-均值聚类算法确定聚类中心的初始最优位置需要计算一个函数值,改变了中心选择的方式,该算法选择样本分布密集,且距离现有簇中心较远的簇作为样本的最优初始位置选择点,具有相对的科学合理性。距离过近的样本簇在使用全局K-均值聚类算法时难免重复运算问题,造成运算结果准确性降低。对改进的全局K-均值聚类算法通过人工模拟数据和学习库中的数据实验测试,得出其相较于改进前算法具有聚类效率提升、误差降低的优势。
算法步骤如下:
第一步:针对样本点xi,计算距离比Vi。中最小的点为xi,将其作为第一个簇的中心,并置q=1(q为簇中心数);
第二步:针对簇中p=1,2,...,q,将xi,i=1,2,...,n划分至最近的簇中,并更新簇中心为第i簇的样本数,由此计算偏差
第三步:置q=q+1,当q>k时,算法结束;
5 实验与结果
通过以下随机生成人工数据集来对改进全局K-均值聚类算法进行验证,其中涵盖噪音数据,以证明改进后全局K-均值聚类算法的抗干扰性能。将数据分为三类,各含有120个二维数据样本,且满足正态分布要求。第i类中横坐标x的均值为纵坐标y的均值为第i类的标准差为在第二类数据中加入噪音点,其标准差为σ1。这三类随机生成带有噪音数据的参数如表1所示,样本分布图如图2所示。

表1 随机生成带有噪音数据的参数
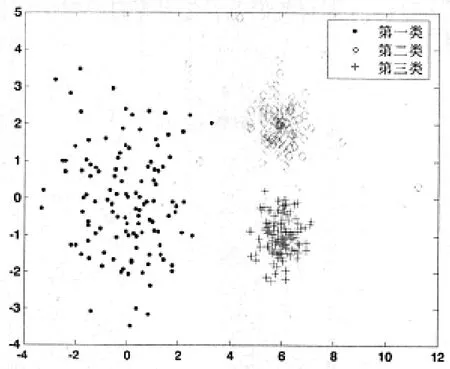
图2 随机生成的样本分布
将全局K-均值聚类算法与改进后算法应用于三类随机数据中,得出的聚类误差平方和(E)和聚类时间(T)如表2所示,聚类结果图如图3所示。

表2 应用二种算法对随机生成数据的聚类结果比较
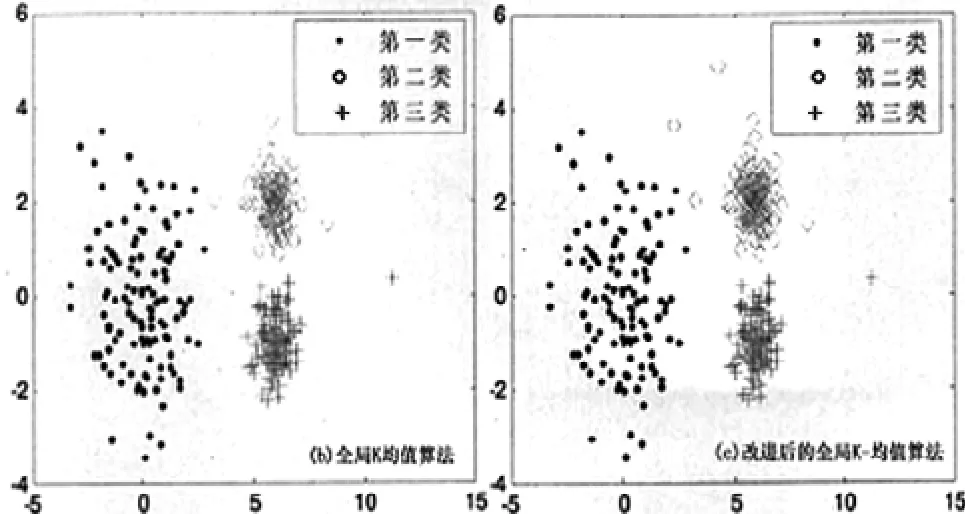
图3 二种算法的聚类结果图
由图3可知,二种算法应用于三类随机生成的带有噪音点的数据中产生了类似的聚类效果,对比全局K-均值算法和改进后算法可知,本文中改进后的算法具有聚类时间短的优点,且改进后的全局K-均值算法基本不受噪音点的干扰。通过实验可知,基于全局K-均值算法改进后的算法聚类效果良好,适合推广应用。
[1]谢娟英,张琰,谢维信,等.一种新的密度加权粗糙K-均值聚类算法[J].山东大学学报(理学版),2010,45(7):1-6.
[2]王军敏,李艳.基于K均值算法的数据聚类和图像分割研究[J].平顶山学院学报,2014(2):43-45.
[3]谢娟英,马箐,谢维信.一种确定最佳聚类数的新算法[J].陕西师范大学学报(自然科学版),2012(1):13-18.
[4]步媛媛,关忠仁.基于K-means聚类算法的研究[J].西南民族学院学报(自然科学版),2009,35(1):198-200.
[5]吴景岚朱文兴.基于K中心点的文档聚类算法[J].兰州大学学报(自然科版),2005,41(5):88-91.
[6]徐辉,李石君.一种整合粒子群优化和K-均值的数据聚类算法[J].山西大学学报(自然科学版),2011,34(4):518-523.
