基于遗传算法的网格任务调度方法分析

2018-01-22金智

电脑与电信 2017年11期

金智

（长沙医学院，湖南长沙 410219）

1 引言

随着互联网信息技术的发展，网格系统也在大量的资源计算中投入使用。网格任务调度能够把各种资源形成一个整体，通过互联网络进行资源的合理分配与共享，从而完成用户的资源请求。而遗传算法是基于生物杂交与变异的研究方法，通过搜索方式、获取过程的优化，来达到全局搜索最优解的目的[1]。遗传算法突破了求导和函数连续性的规则限制，在多种智能信息处理领域得到广泛应用。

2 网格任务调度的问题描述与定义

在任务信息、资源信息和任务时限确定的情况下，运用遗传算法进行任务的执行之前，本文主要进行以下的问题定义：在NxM的矩阵[N,M]中，Time[i,j]代表任务Ti在资源Rj上中的任务处理时限。T={T1、T2、T3、……、Tm}，代表任务集合；R={R1、R2、R3、……、Rn}，代表资源集合。

网格任务间的依赖关系，可以用有方向无环路的图表进行表示。在G=(T，E，V)这一有方向无环路图表中，T代表任务集合，E代表网格任务关系图中的边数集合，V代表给定边的权合集。G=(T，E，V)上的一个割将该图的顶点分成两个子集：V＝A＋B，而（Ti，Tj）∈E代表Ti任务先执行，Ti执行完毕后再执行Tj，其中Ti和Tj属于前项与后项的关系。将A设置为有方向无环路图表的调度方案，WAS(A)代表A调度方案中资源集合所耗费的任务时限，公式为WAS(A)=max{WA(Ri)，i=1，……，n}。因此在网格任务调度中，需要选择恰当的调度方案，以尽可能降低资源集合所耗费的任务时限[2]。

对于有方向无环路的任务图表，其中顶端阶段的深度值为1，由根节点往下每增加一层深度值也相应加1，而任务图表的高度值则与深度值的算法相反。设Ti为有方向无环路数据结构中的某一节点，Ti的前项可以用固定在前面的pre（Ti）表示，Ti的深度值用 H（Ti）表示。

在有方向无环路任务图表中，对每个网格任务的深度值进行计算，通过以上计算可以得出：若任务图表中的最大深度值为h，则该网格的任务集合就有h个。从图1中可以看出：{T1，T2}深度值为1，{T3，T4}、{T4，T5}的深度值为 2，{T6，T7}的深度值为3。若该网格中有R1、R2两个资源集合，则需要对图1的h个任务集合进行两两排列，则总的任务执行序列为{T1，T2，T3，T4，T5，T7，T6}，也就是按照{R1R2，R1R2，R1R2，R1}的资源分配方式进行分配。在该网格任务调度中，主要运用非降序的深度数值排列方式，进行任务依赖关系的表示，因此该排序属于合理的任务调度方法。网格任务调度的图1如下所示[3]：

图1 网格任务依赖关系图

3 基于遗传算法的任务调度算法设计

3.1 网格任务调度的编码

在网格任务调度的二进制编码中，由于存在能够复制的对偶基因，而产生相应的任务调度问题。所以运用实数1和0的字符串进行编码，能够有效解决等位基因的问题。实数1和0的字符串编码，其主要存在搜索范围广、搜索精度高等特征。米凯利维茨在《遗传算法和数据编码结合》一书中表明：二进制编码是具有层次性的进化个体，而实数编码的每个基因位用某一范围内的一个浮点来表示，个体的编码长度取决于决策量的个数[4]。

网格任务调度的编码规则为：假设网格有m个任务集合、n个资源集合，选择[1,n]之间的m个整数集合，共同组成G染色体集合G=[g1，g2，g3，……，gn]其中g[j]代表染色体中单个基因的编号，g[j]可以是[1,n]集合中的任意一组数值，[1,n]代表资源集合编号。大多数染色体中的基因数值都不相同，但也有某些基因数值是相同的，相同的基因数值代表不同任务在相同资源集合中完成。

3.2 网格任务调度的遗传操作

3.2.1 遗传算法的复制与选择

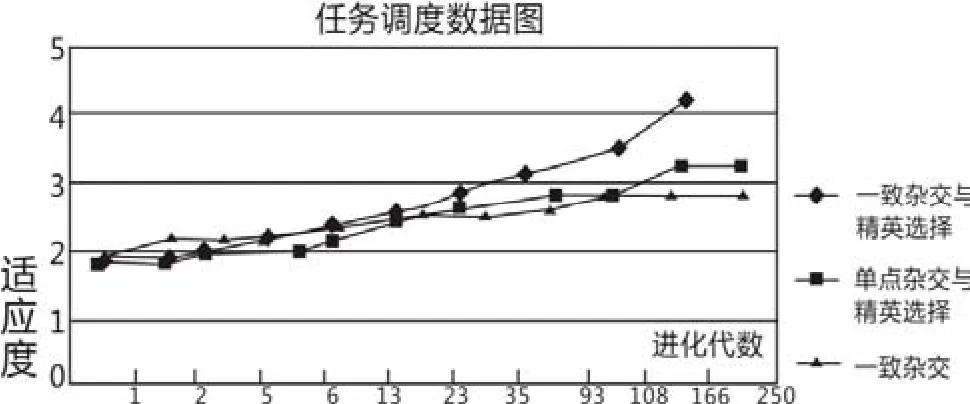
根据以上公式计算出网格任务适应度数值后，将各个适应度数值采用轮赌盘进行群体中的个体选择。例如：个体1、2、3对应的适应度分别为2、3、1，则相应累计概率为2/6、(2+3)/6和(2+3+1)/6，生成一个随机函数为rand()。如果rand()<2/6则选中个体1，如果2/6

遗传算法的杂交，主要为模拟基因进化的有性繁殖过程。其通过基因重组将良性基因传递给下一代，并完成复杂的基因重组操作。遗传算法的杂交主要包括以下几方面内容：(1)设定交叉概率Pc；(2)随机生成[0，1]间的数b，若b

本文使用均匀杂交的遗传算法，对实数1和0的字符串进行同概率杂交。设生成的新杂交个体为：s1'={a11，a12，……，a1L}，s2'={a21，a22，……，a2L}，具体公式如下所示 U(Pc，x)：均匀分布的变量）

3.2.3 遗传算法的变异

遗传算法的变异，主要仿照同一基因库中不同个体之间的分子差异，而进行实数1和0的字符串进化的方法。遗传算法将变异算子作用于群体，对群体中个体串某些基因座上的基因值进行变动，其变动的概率也为P。但遗传算法的变异，主要为了改善个体杂交后的适应度数值，从而帮助全局进化达到最优解。因此遗传算法变异对个体基因信息的改动很小，通过弥补对偶基因的丢失，来促进群体中个体差异的增大。因此杂交操作后引入变异，能够有效提升遗传算法的搜索性能。

4 基于遗传算法的仿真实验及结果分析

遗传算法仿真实验的主要参数为：交叉概率Pc=0.8、变异概率Pm=0.15、种群个数P=80和迭代次数G=300。同时将一致杂交与精英选择、一致杂交、单点杂交与精英选择的数值，放入任务数据图表中，具体如图2所示：

图2 任务调度数据图

从以上数据表中可以得出：遗传算法在进化代数较小的时候，三种数据的适应度收敛的速度很快。而随着优良个体的筛选与排除，多个种群的适应度数值开始增大，但其收敛速度则开始减小。通过遗传算法变异对个体基因信息的改动，使得算法的全局进化达到最优解。而且一致杂交与精英选择相结合的遗传算法，适应度收敛速度明显高于其他两个种群，遗传变异也最可能达到全局最优解。而单单使用一致杂交的遗传算法，其种群适应度数值的波动性较小，这表明一致杂交的遗传算法最可能达到局部最优解。而单点杂交与精英选择的遗传算法，其达到最优解的可能性较低，一般不采取该算法进行任务执行。