基于XGBoost模型的股骨颈骨折手术预后质量评分预测

贾文慧，孙林子，景英川

(1.太原理工大学 数学学院，山西 晋中 030024; 2.苏州大学 第一临床学院，江苏 苏州 215000)

股骨颈骨折是临床上常见的骨折之一，股骨颈骨折手术预后质量评分(Harris评分)是骨科医生较为关注的问题[1]。随着病例数据的累积，可利用Harris评分对病例数据进行分类预测。而面对大数据时代数据海量化、复杂化和异质化的新挑战，XGBoost模型以其高效、灵活和准确的特点成为解决分类问题的常用工具之一[2]。XGBoost 是极端梯度上升(Extreme Gradient Boosting)的简称，它兼具线性模型和Boosted Tree模型的一种优化模型[3]。由于XGBoost模型对具有输入数据要求不高、自动变量选取、计算复杂度不高等优势，被统计学、数据挖掘、机器学习等专家广泛应用于统计学习、数据分析和人工智能等领域。特别是在医疗领域，XGBoost模型可利用历史病例数据构建模型并进行分类预测。当新患者病例出现时，依据相关病例信息，可直接进行预测，帮助医生做出更加合理且有效的判断，有助于指导后续医疗工作。

医学领域学者对股骨颈近端骨折的病例做了大量研究，以股骨颈病患的临床研究和试验研究居多[1,4]。本文开创性地使用XGBoost模型，对股骨颈骨折的相关数据进行了分析，并利用使用最为广泛且认可度最高的Harris评分标准[5]对股骨颈骨折的近期疗效做了相应的评价。Harris评分是由HARRIS(1969)提出的一套适用于各种髋关节疾患的疗效数值评价标准。其满分为100分，90分以上表示手术疗效优良；80～89分表示手术疗效较好；70～79分表示手术疗效尚可；低于70分表示手术疗效较差。在临床研究中，骨科医生认为Harris评分大于70分的是“成功”手术，而小于70分的则为“不成功”。为方便临床医生的应用，笔者将Harris评分作为一个二分类问题解决。由于影响Harris评分结果的因素较多，本文将采用XGBoost模型建立预测精度高且高效的分类模型。建立Harris评分分类模型后，可依据患者的自身情况、手术状况等方面的信息进行股骨颈骨折近期疗效的准确预测，这一模型的建立，将会给临床实践带来积极的影响[3]。

1 XGBoost算法介绍及建模过程

XGBoost(Extreme Gradient Boosting)算法是一种大规模并行Boosted Tree的模型。而Boosted Tree最基本的组成被称作回归树(regression tree)，也称CART.以判断一个人是否喜欢玩电脑游戏的回归树为例[2](如图1所示)，简单说明了回归树是依据输入若干因素的属性并将其分配到每一叶子节点上，且每一叶子节点对应一个预测的实数分数。通常仅依据一棵回归树是无法准确的对数据进行预测，因而，将会采用多棵回归树对同一问题进行分类判断。根据图1的例子，构造出如图2所示的两颗回归树进行分类预测，每个样本的预测结果即为每棵树预测的分数之和。

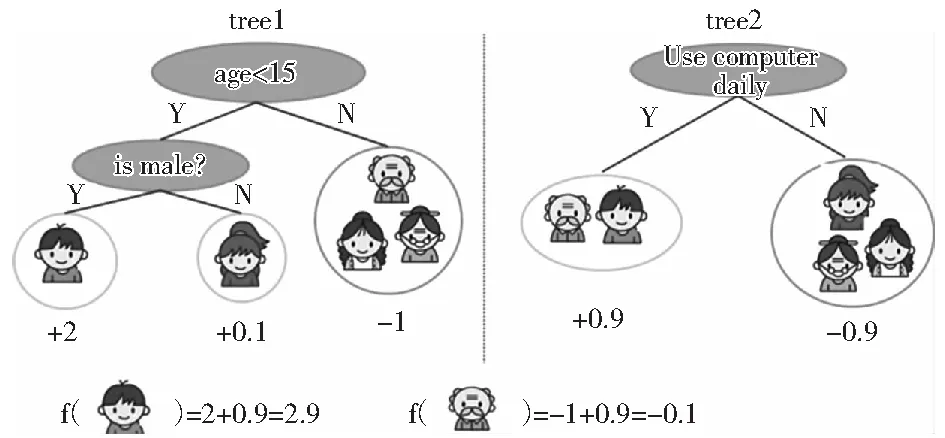
图2 两棵回归树预测模型Fig.2 Two-trees regression prediction models

将XGBoost模型可表示为：

当建立模型时，需要找到最优的参数，通常选择采用使目标函数值为最小的参数[6]。一般目标函数包含：误差项L(θ)(误差函数)和正则化项Ω(θ)(衡量模型的复杂度)两项。将目标函数fobj(θ)表示为：

fobj(θ)=L(θ)+Ω(θ) .

式中，分别定义

当对训练数据进行学习时，每次在保留原有模型不变的基础上，加入一个新的函数f，观察对应的目标函数，若加入新的函数使目标函数尽可能减到最小，则将该函数加入到模型中。过程如下：

式中，C表示与f无关的常数项[1]。

之后，对目标函数进行泰勒展开得到如下的近似目标函数：

当去掉常数项C时发现，目标函数只依赖于每个数据点在误差函数上的一阶和二阶导数。

下面讨论目标函数中模型复杂度的定义。首先，对f细化，可将回归树划分为树的结构部分q和叶子权重部分ω，即：

ft(x)=ωq(x),ω∈RT,q∶RT→{1,2,…,T} .

结构部分q把输入变量映射到叶子的索引号上，权重ω给定了每个索引号对应叶子的实数分数值。接下来，将模型的复杂度定义为每棵回归树中节点的个数与其叶子节点对应的实数分数值的平方的和。即

式中，γ,λ是调整参数，防止模型过度拟合。此时，可将目标函数进一步表示为：

式中，Ij={i|q(xi)=j}表示第j棵树中每一叶子中的样本集合，令

即

这时，假设树的结构部分q已知，则可通过此目标函数来找到最好的ω，及其对应目标函数的最大增益，其实是将需要解决的问题转化为求解二次函数的最小值问题。解得：

式中，fobj作为评价模型的打分函数，fobj值越小，代表对应模型越好[1]。接下来，需要列举大量的回归树结构，使用fobj找到最优的树结构，放到已有模型中，重复以上方法，建立最优的Boosted Tree.但列举全部的回归树的结构不太现实，因此，采用“贪心法”，即每次对已有的叶子加入新的分割，并计算因此获得的最大增益。对于具体的分割方案，可获得的增益计算公式如下：

式中，第1项表示分割后左子树产生的增益，第2项表示分割后右子树产生的增益，第3项表示不进行分割的增益，γ表示由于分割加入新叶子带来的复杂度代价。

为了进行高效的分割，需要具体计算对某一分割左右的导数，对于所有分割，只需按上述方法计算导数即可。值得注意的是，由于分割加入新叶子后会带来增加复杂度的代价，因此加入新的分割不一定总是件好事。

以上推导了Boosted Tree的学习过程，了解到Boosted Tree的实质，这有利于将此方法直接应用于解决实际分类问题中。本文使用XGBoost方法的实质就是在单个多CPU计算机上并行Boosted Tree，提升Boosted Tree的预测精度[2,6]。

2 股骨颈骨折手术Harris评分预测模型

股骨颈手术预后质量分析，主要是对Harris评分进行分类。根据已有研究表明[3-4]，影响Harris评分结果的因素变量较多，主要有患病年龄、患者性别、骨折类别、致伤原因、身体质量指数、是否患有糖尿病、是否饮酒、是否吸烟、pauwl分型类型、garden分型类型 、手术持续时间、手术解剖部位、正位螺钉是否平行、侧位螺钉是否平行、受伤至手术时间、复位质量、复位过程是否穿透股骨头、螺钉是否至软骨下、是否为三角结构、经过股骨距是否合理、患者术后不负重时间是否合理、骨折是否愈合等。

本文数据来自山西医科大学第二附属医院骨科，2014年10月—2016年10月股骨颈病患的数据。依据大量的相关研究[1,5]，收集了上述22个影响Harris评分结果的自变量，及“成功”与“不成功”两类评分因变量，共采集病例样本数80例。由于数据样本量有限且影响Harris评分的变量较多，同时希望能高效利用数据信息，因此，采用XGBoost模型对这一数据进行分析研究。

2.1 数据预处理

数据预处理对于模型建立有至关重要的作用，能够直接影响最终预测结果。收集数据涉及较多的变量，且变量类型复杂，原始数据的自变量中有8个多分类变量和14个二分类变量(见表1)。为方便建模，将变量矩阵改写成数值矩阵，其中多分类变量被有序分类，如患病年龄分为如表2所示的v1(18岁以下)、v2(18—50岁)、v3(51—70岁)和v4(70岁以上)。另外，需要把因变量和自变量分离，并在XGBoost模型中分别指定数据集。将75%的数据设为训练集，25%的数据设为测试集。

表1 原始数据自变量及取值Table 1 Variables and values of data

表2 部分多分类变量的有序分类Table 2 Part of the multivariate orderly classification

2.2 设定调整参数

在XGBoost模型中最为重要的一步就是确定调整参数值。需要确定的参数主要有γ，λ回归树的最大深度等，取值范围分别为0到1，0到∞，1到∞；默认值分别为0.3，1，6.由于R语言程序中已有成熟的XGBoost模型的程序包xgboost，可以直接使用其设定的参数取值。此外，也可以通过C++、python等程序完成这一步骤。

2.3 模型建立及结果分析

由于影响Harris评分的变量众多，本研究数据涉及22个相关变量。由于变量并不是越多越有利于模型的建立，为高效地建立XGBoost模型，故使用主成分分析法对数据进行进一步的处理[7]，得到了与Harris评分相关性较大的5个影响因子，分别是：患者年龄、身体质量指数、pauwl分型类型、garden分型类型和手术解剖部位。接下来，我们可以直接利用R语言程序进行XGBoost建模过程。此外，由于数据样本量较为有限，为充分利用样本信息，本研究根据实际经验进行了500次大量重复建模过程，每次从样本总体中随机抽样75%的样本量作为训练集，剩下25%的样本量作为测试集。

使用未经主成分分析处理的数据建立的XGBoost模型，该模型的分类预测准确率为87.36%，经主成分分析处理后的数据建立的XGBoost模型，模型的分类预测准确率达90.57%，预测值方差为0.004，而这一结果说明了主成分分析对数据处理的有效性。由XGBoost模型的预测准确率可知，XGBoost模型对股骨颈骨折病例数据的拟合程度较高且稳定性好，XGBoost模型可以帮助骨科医生处理Harris评分分类的相关问题。

3 结论

在建立XGBoost模型前，通过对数据的处理，找到患者年龄、garden分型、pauwl分型类型等5个与Harris评分相关度较高的主成分，使得XGBoost建模过程更为高效。同时发现，数据中较多变量与Harris评分的相关度低，因此，基于XGBoost建立的股骨颈骨折Harris评分模型，能够为骨科医生在临床预测Harris评分起到指导作用。

从XGBoost模型的分类预测准确度方面来看，在股骨颈数据上搭建XGBoost模型是成功的，有较高的预测精度、良好的稳定性及运行的高效性。XGBoost模型虽广泛应用于数据挖掘与人工智能领域，但经研究表明，XGboost模型是可以推广到相关医疗领域中。同时，利用XGBoost建立的股骨颈骨折Harris评分模型的封闭性较高，不能直观地看到模型的建立过程，模型的复杂程度高。本研究由于数据样本量有限，未能建立预测效果更为准确的XGBoost模型，这将成为后续研究中需要改进的问题。

[1] 李瑞龙,张强.股骨颈骨折的外科治疗进展[J].医学综述,2011，17(14)：2127-2129.

LI R L,ZHANG Q.Advances in surgical treatment of femoral neck fracture[J].Medical Recapitulate,2011，17(14)：2127-2129.

[2] CHEN T Q,GUESTRIN C.XGBoost:A scalable tree boosting system[C]∥ACM.Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM,2016:785-794.

[3] 吴险峰,尚希福.股骨颈骨折治疗进展[J].医学综述,2008,14(12):1873-1876.

WU X F,SHANG X F.Progress in therapy of femoral neck fractures [J].Medical Recapitulate,2008,14(12):1873-1876.

[4] LIPORACE F,GAIN R,COLLING C et al.Result of internal fixation of pauwels type-3 vertical fernoral neck fractures[J].J Bone Joint Surg Am,2008,90(8):1654-1659.

[5] 艾自胜,张长青,刘粤，等.股骨颈骨折内固定术后随访资料的Harris评分分析[J].中国修复重建外科杂志,2009,23(4):435-439.

AI Z S,ZHANG C Q,LIU Y,et al.Analysis on Harris scores at follow-up after internal fixation of femoral neck fracture[J].Chinese Journal of Reparative and Reconstructive Surgery,2009,23(4):435-439.

[6] FRIEDMAN J H,POPESCU B E.Importance sampled learning ensembles[J/OL].CiteSeerX,2003:1-32[2003-09-09].https://www.researchgate.net/publication/2888930_Importance_Sampled_Learning_Ensembles.

[7] 林海明,杜子芳.主成分分析综合评价应该注意的问题[J].统计研究,2013,30(8):25-31.

LIN H M,DU Z F.Some problems in comprehensive evaluation in the principal component analysis[J].Statistical Research,2013,30(8):25-31.