融合结构对城市轨道交通列车组合测速定位精度的影响

刘豪鹏 董德存 庄倩倩 翟亚婵

（1.同济大学交通运输工程学院，201804，上海；2.北京全路通信信号研究设计院集团有限公司，100070，北京∥第一作者，硕士研究生）

随着城市轨道交通运行控制的发展，无论是ATP（列车自动保护）的超速防护，ATO（列车自动运行）的自动驾驶和定点停车，还是ATS（列车自动监控）的列车追踪显示，这些功能都与列车测速定位息息相关。单一的测速定位传感器逐渐难以满足CBTC（基于通信的列车控制）和移动闭塞列车测速定位的性能需求，采用多元传感器，通过信息融合的方法提高列车组合测速定位性能成为一种值得研究的解决方案。

测速定位传感器、融合算法和融合结构是决定列车组合测速定位方案性能的三个要素。其中，融合结构决定列车组合测速定位方案的基本框架，不同的融合结构方案的精度、复杂度、实时性、容错性、成本等均有不同。本文将在采用相同传感器、融合算法的前提下，研究不同融合结构对基于信息融合的列车组合测速定位精度的影响。

1 融合结构综述

基本的融合结构包括集中融合结构和分散融合结构。集中融合结构局部输出的是测量值，分散融合结构局部输出的是估计值。分散融合结构中又有两种具有代表性的结构，即级联融合结构和联邦融合结构。此外，在复杂的特殊应用中，可形成分层次的多级融合结构或将集中融合结构与分散融合结构组合形成的混合结构［1］。

1.1 集中融合结构

集中融合结构如图1所示，各传感器的量测值Z直接送入一个集中滤波器中进行融合，得到最优估计值＾Xg和估计误差协方差阵Pg。图1中，虚线的反馈通道可视传感器情况配置，“黑箱”结构的传感器可能不接受反馈。

图1 集中融合结构示意图

1.2 分散融合结构

分散融合结构中的级联融合结构如图2所示，是一种松耦合的结构，分为子滤波器和主滤波器两层。主滤波器的＾Xg和Pg通过信息分配系数β反馈回子滤波器。

图2 级联融合结构示意图

联邦融合结构如图3所示，设参考传感器，在子滤波器部分将参考传感器和辅助传感器信息融合，再送入主滤波器融合。联邦融合结构适用于采用间接法估计测速定位参数误差量的系统。

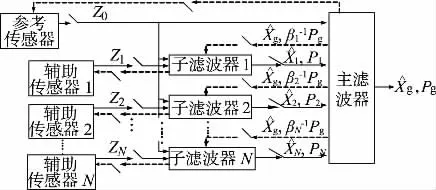
图3 联邦融合结构示意图

由于多级融合结构及混合融合结构仅在某些特殊情况下应用，本文将主要分析集中融合结构与分散融合结构中的级联融合结构对列车组合测速定位精度的影响。

2 集中融合结构及级联融合结构在列车组合测速定位中的应用

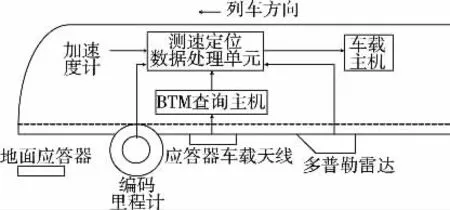
图4 列车组合测速定位系统构成

本文构建如图4所示的城市轨道交通列车组合测速定位系统。其主要由编码里程计、DRS05型多普勒雷达、ADXL105型加速度计实现速度测量及相对定位，并设S21型应答器进行绝对位置校正。

选取工程中常用的标准卡尔曼滤波作为本系统的融合算法。本文分别应用集中融合结构与级联融合结构构建列车组合测速定位案。

2.1 集中融合结构在列车组合测速定位中的应用

集中融合结构的列车组合测速定位系统工作流程见图5。来自多普勒雷达、编码里程计的速度测量值及来自加速度计的加速度测量值，经过硬同步或软同步处理后确保时间和空间上的一致性，经过数据预处理除去空滑误差、温漂误差等非高斯噪声，通过故障检测和隔离单元除去“坏值”；然后将有效数据送入集中滤波器中，通过标准卡尔曼滤波算法对列车状态进行估计。

标准卡尔曼滤波算法应用于列车测速定位时，需建立线性列车系统状态方程及传感器量测方程。所建的匀变速列车系统状态模型见式（1）。其中，列车k-1时刻的位移、速度、加速度分别为lk-1、vk-1、ak-1，Wl，k-1,Wv，k-1，Wa，k-1为对应系统噪声，采样周期Ts=0.1 s［3］。

集中融合结构的传感器量测模型见式（2）。

式中：

vodo，k，vdop，k，aacc，k——分别为k时刻编码里程计、多普勒雷达和加速度计的测量值；

kodo，kdop，kacc——分别为误差分析得到的对应误差系数；

Vodo，k，Vdop，k，Vacc，k——分别为对应量测噪声；

modo，mdop，macc——分别为对应的传感器故障隔离系数，其正常值为1，故障值为0。

2.2 级联融合结构在列车组合测速定位中的应用

级联融合结构的列车组合测速定位系统工作流程见图6。来自多普勒雷达、编码里程计的速度测量值及来自加速度计的加速度测量值经过同步处理及数据预处理后，先采用检测法进行故障检测，再分别送入对应的标准卡尔曼子滤波器中滤波。通过故障隔离单元将有效的滤波值送入主滤波器中进一步融合估计。

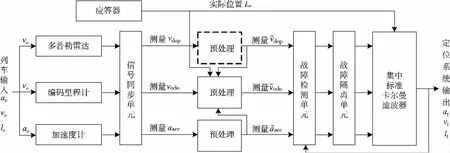
图5 集中融合结构标准卡尔曼滤波列车组合测速定位系统的工作流程

图6 级联融合结构标准卡尔曼滤波列车组合测速定位系统工作流程

级联融合结构的列车系统状态方程与集中结构相同，可见式（1）。子滤波器1的多普勒雷达量测方程见式（3）。

子滤波器2的编码里程计量测方程见式（4）。

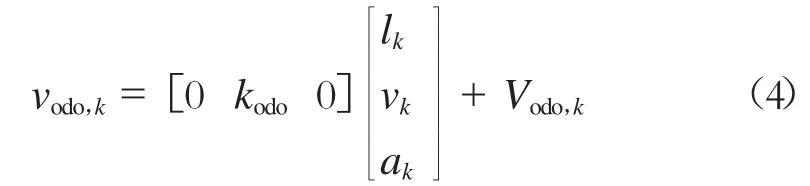
子滤波器3的加速度计量测方程见式（5）。

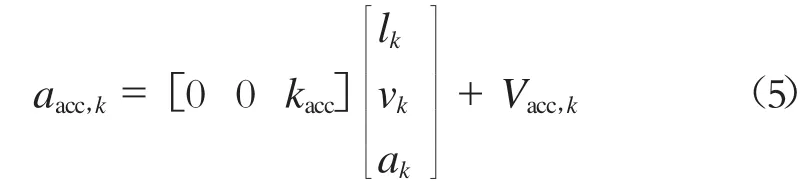
估计信息全部来源于各子滤波器，主滤波器只起合成作用。主滤波器可采用加权平均原理。其权值即为前面提到的信息分配系数β，也用于反馈。子滤波器提供的信息量与其估计协方差成反比。编码里程计的信息分配系数见式（6），其中，P为估计误差协方差阵，多普勒雷达与加速度计的信息分配系数同理。

在实际应用中，上述信息分配系数确定法可能使矩阵中元素数量级降至10-16以下，从而形成发散，故可采用如式（7）所示的基于速度的信息分配系数确定法。其原理为各传感器的测速精度变化随速度变化呈现规律性。其中，分别对应于编码里程计、多普勒雷达、加速度计的传感器故障隔离系数nodo、ndop、nacc，其正常值为 1，故障值为 0。

3 集中融合结构与级联融合结构列车组合测速定位精度仿真比较

通过所建立的系统模型和量测模型，采用标准卡尔曼滤波算法，在Matlab中分别仿真同一场景下集中融合结构与级联融合结构列车测速定位方案的精度，并进行定性定量比较。

3.1 集中融合结构及级联融合结构列车组合测速定位精度定性比较

仿真场景：设城市轨道交通A、B两站相距1 600 m，且为无隧道、平直、无限速的理想状态。假设列车以启动-加速-匀速-惰行-制动策略运行，取采样时间间隔Δt=0.1 s。

仿真流程见图7。通过列车运行动力学分析，得到列车运行控制曲线，加入有色噪声仿真实际运行曲线；在实际速度中加入空滑、轮径磨损等误差及其他高斯性误差仿真编码里程计测速值，在实际速度中还加入车体震动、安装及频率测量等误差仿真多普勒雷达测速值；在实际加速度中加入初始偏差，以及温漂、安装等测加速度值误差。预处理之后分别送入集中融合结构和级联融合结构滤波器，将其估计加速度、速度及位移进行比较。

通过在Matlab中执行图7的仿真流程，可分别得到集中融合结构及级联融合结构对加速度、速度及位移的估计误差曲线。通过误差曲线可知，集中融合结构系统的测速定位精度整体高于级联融合结构，其优势在加速度的估计上尤为明显。主要原因在于级联融合结构是一种松耦合结构，在主滤波器融合过程中丢失部分信息，加速度计的加速度估计精度高，编码里程计和多普勒雷达的加速度估计精度低，“中和”后的加速度精度低于加速度计的估计精度。

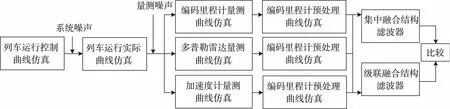
图7 仿真流程

3.2 集中融合结构及级联融合结构列车组合测速定位精度定量比较

通过计算在Matlab中运行100次集中融合结构及级联融合结构列车组合测速定位仿真代码的平均均方根误差，可以实现对集中融合结构及级联融合结构列车组合测速定位系统精度的定量比较。运行100次集中融合结构及级联融合结构列车组合测速定位仿真代码，其加速度计测量均方根误差、加速度计预处理均方根误差、集中融合结构和级联融合结构的加速度估计均方根误差见图8。计算这100次运行测加速度均方根误差的平均值见表1。

运行100次集中融合结构及级联融合结构列车组合测速定位仿真代码，其编码里程计、多普勒雷达、加速度计测速均方根误差的集中融合结构和级联融合结构测速估计均方根误差见图9。计算这100次运行测速均方根误差的平均值见表2。

表1 运行100次各算法平均测加速度均方根误差

表2 运行100次各算法平均测速均方根误差

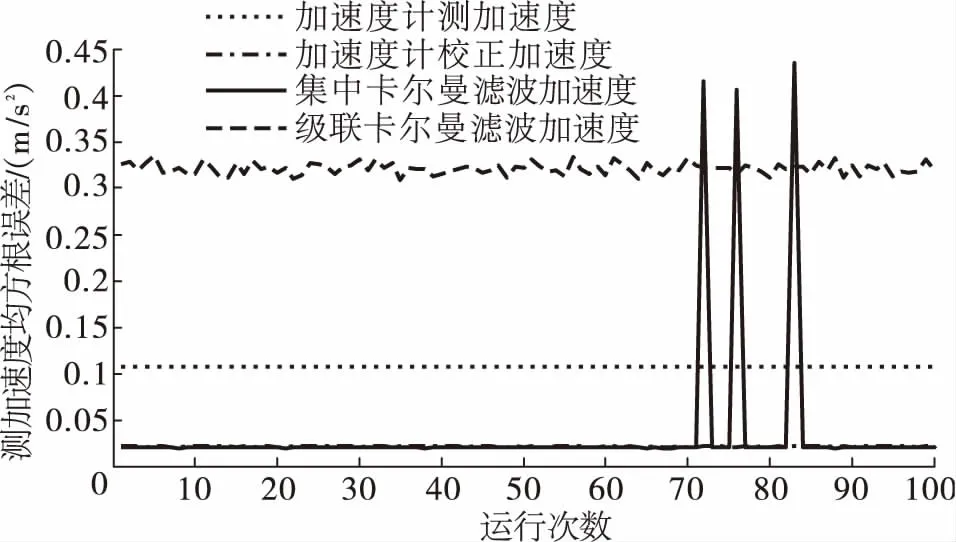
图8 运行100次的各算法测加速度估计均方根误差曲线

图9 运行100次的各算法测速估计均方根误差曲线

运行100次集中融合结构及级联融合结构列车组合测速定位仿真代码，其编码里程计、多普勒雷达的集中融合结构和级联融合结构定位估计均方根误差见图10。计算这100次运行的定位均方根误差的平均值见表3。

图10 运行100次的各算法定位估计均方根误差曲线

表3 运行100次各算法的平均定位均方根误差

对上述仿真结果进行分析，可得到如下结论：融合结构对列车组合测速定位精度具有较大影响，集中融合结构比级联融合结构具有更高的测速定位精度，对加速度的估计优势最为突出。

4 级联融合结构在列车组合测速定位应用中的改进

通过上述分析可知，集中融合结构比级联融合结构具有更高的测速定位精度，但是通过图8可知，级联融合结构比集中融合结构更为稳定（集中融合结构中有三个发散的波峰）。此外，级联融合结构可以降低主滤波器的运算量和复杂度，可以提高信息处理的实时性，具有其本身的优势。故本文提出一种基于精度的a-v-l分离的信息分配系数确定法，旨在提高级联结融合构列车组合测速定位方案的精度。

基于精度的a-v-l分离的信息分配系数确定法将加速度、速度、位置分离，分别配置信息分配系数，见式（8）。

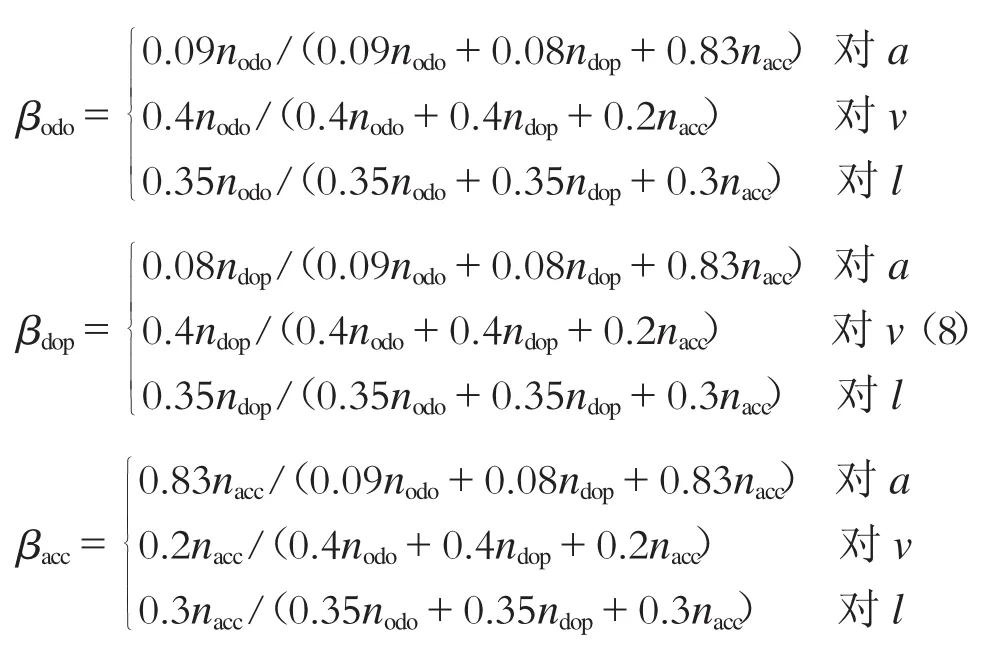
该改进算法对于加速度的估计误差见图11。该改进方案可部分改进原级联融合方案的加速度估计精度，误差较大处是由于通过检测法判定加速度计故障失效而导致的。

运行100次级联及改进级联融合结构列车组合测速定位仿真代码，其测加速度估计均方根误差见图12，测速度估计均方根误差见图13，定位估计均方根误差见图14。计算这100次运行测加速度、测速、定位均方根误差的平均值见表4。

表4 运行100次各算法平均估计均方根误差

图11 改进级联融合结构列车组合测速定位系统测加速度误差曲线

图12 运行100次的测加速度估计均方根误差曲线

图13 运行100次的测速估计均方根误差曲线

图14 运行100次的定位估计均方根误差曲线

通过上述仿真结果，可得到如下结论：本文提出的a-v-l分离的信息分配系数确定法可在一定程度上改善原级联融合结构列车组合测速定位精度，其中，对测加速度估计的改善作用比较明显。

5 结语

融合结构对基于信息融合的列车组合测速定位性能具有较大影响。本文通过仿真分析，证明了集中融合结构的测速定位精度高于级联融合结构。为充分利用级联融合结构具有降低滤波中心运算量、提高融合系统实时性等优势，本文提出a-v-l分离的信息分配系数确定法，并通过仿真证明了该方法可在一定程度上提高原级联融合结构算法的精度。

［1］ 中华人民共和国铁道部．铁路行车事故案例选编［M］.北京：中国铁道出版社，1999.

［2］ 万德钧，房建成，王庆.GPS动态滤波的理论、方法及其应用［M］.南京：江苏科学技术出版社，2000.

［3］ 袁振江.列车组合定位系统多传感器信息预处理技术研究［D］.北京：北京交通大学，2007.

［4］ 顾启泰，王颂.联邦滤波器理论研究［J］.中国惯性技术学报，2002，10（6）：34.

［5］ 纽瑞萍，蔡伯根.一种加速度计误差修正方法的研究［J］.传感器技术，2002，21（4）：4.

［6］ 顾桂梅，高渐强.基于H～∞鲁棒滤波技术的列车组合定位方法研究［J］.自动化与仪器仪表，2012（3）：40.

［7］ 曹长虹.城市轨道交通列车定位方法研究［D］.兰州：兰州理工大学，2011.

［8］ BASS R W.Kalman filtering：theory and practice［J］.Proceedings of the IEEE，1996，84：321.

［9］ LIU C Y，SHUI P L，LI S.Unscented extended Kalman filter for target tracking ［J］.Journal of Systems Engineering and Electronics，2011，22（2）：188.