施工控制网复测起算点可靠性研究
2018-01-21李忠峰赵浩鹏张海龙
李忠峰,赵浩鹏,张海龙
(西北电力设计院有限公司,陕西 西安 710032)
1 概述
根据《火力发电厂工程测量技术规程》(DL/T 5001-2014)第10.1.11的要求,“厂区控制点应采取保护措施,并在施工期间每隔3~6个月复测一次”的规定,对于施工控制网的复测已成为日常重点工作,其关系到施工放样的准确性和建构筑物之间连接的正确性。
众所周知,火力发电厂是一个由多个分部工程组成的系统工程,由于施工现场是多道工序组成的,基础开挖、地基处理、大型车辆运输、龙门吊起吊重物及施工过程中会产生震动,高大建筑物封顶后对地面施加的压力,这些因素会对测量控制点的稳定性产生负面影响。同时,自然雨水的侵蚀以及管道漏水的浸泡都会加速控制点的沉降和位移。要排除这些因素对控制网精度的影响,复测过程中选择数据可靠、点位稳定的控制点作为起算数据,使整个控制网数据前后统一、保证放样数据的一致性具有现实意义。
施工控制网复测是基于控制点在上述环境中其点位稳定性发生了变化,且因位置不同,变化不一;有的点位稳定性发生了变化,有的点位稳定性未发生变化,这种现象难以用直观的方法识别。因此,如何判断起算控制点的可靠性,显得尤为重要。针对此问题,本文运用误差理论知识,计算高程较差中误差、距离较差中误差的方法,通过观测计算,筛选出稳定点位,达到解决问题的目的。
2 高程较差、距离较差的限差计算
本文以某电厂建立施工控制网和复测为实例。该电厂首次高程控制网使用三等水准建立。采用“测量控制网平差系统HLADJV3.0”进行平差计算,平差后每km高差中误差±1.0 mm,起始点相对于最弱点高差中误差±1.0 mm,各项精度指标满足技术规程的要求。平面控制网采用四等导线建立,采用“测量控制网平差系统HLADJ V3.0”进行平差计算,平差后测角中误差mβ=±0.7″,最弱边相对精度为1/140000,最弱点点位中误差±2.1 mm。成果见表1。
2.1 高程较差的限差计算
假定第二次水准测量采用同精度观测,则起始点相对于最弱点高差中误差在±1.0~±2.0 mm之间。考虑到施工场地控制点稳定性发生了变化,起始点高程中误差按考虑。
则有:ΔH=H首次-Hi
高程较差中误差:

高程较差的限差:

即所有控制点在保持稳定状态下,首次计算的高程(或i-1次)与第i次计算的高程较差不得大于3.0 mm(或5.0 mm)。关于高程较差的限差取值范围见本文6.2。
2.2 距离较差的限差计算
由平面控制平差报告可知,最弱边相对精度1/140000,则有:
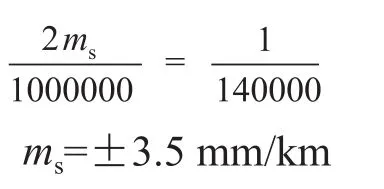
距离较差的限差:

或直接使用仪器标称精度指标,如TC1201的测距精度为:1+1.5 ppm,则:
距离较差的限差:

火力发电厂一般占地面积大约在800 m×1000 m左右,施工控制网边长大于500 m的概率较小,用500 m作为参考值,则:距离较差的限差采用±5.0 mm较为适宜。
2.3 算例
2013年10月完成了某电厂建立施工控制网的测量工作,2015年3月业完成施工控制网复测,经现场实际测量,其成果见表1。

表1 某电厂工程控制点成果
3 高程较差中误差及距离较差中误差的计算

式中:V为高程较差,V=H首次-Hi;改正数为(VV中数);n代表点数。
计算距离较差中误差、距离较差中数的公式与(1)、(2)相同。
4 对比分析
就本次复测的成果进行对比,依据误差理论确定起算点。高程较差统计表分为三类。
第一类:随意选取某个控制点作为起算点,计算结果见表2。

表2 第一类高程较差统计
第二类:对某一测段或两段的高差进行了检测,主观上有倾向性选择某控制点作为起算点,计算结果见表3。

表3 第二类高程较差统计
第三类:采用高程较差和的中数作为依据,选出的控制点作为起算点,计算结果见表4。
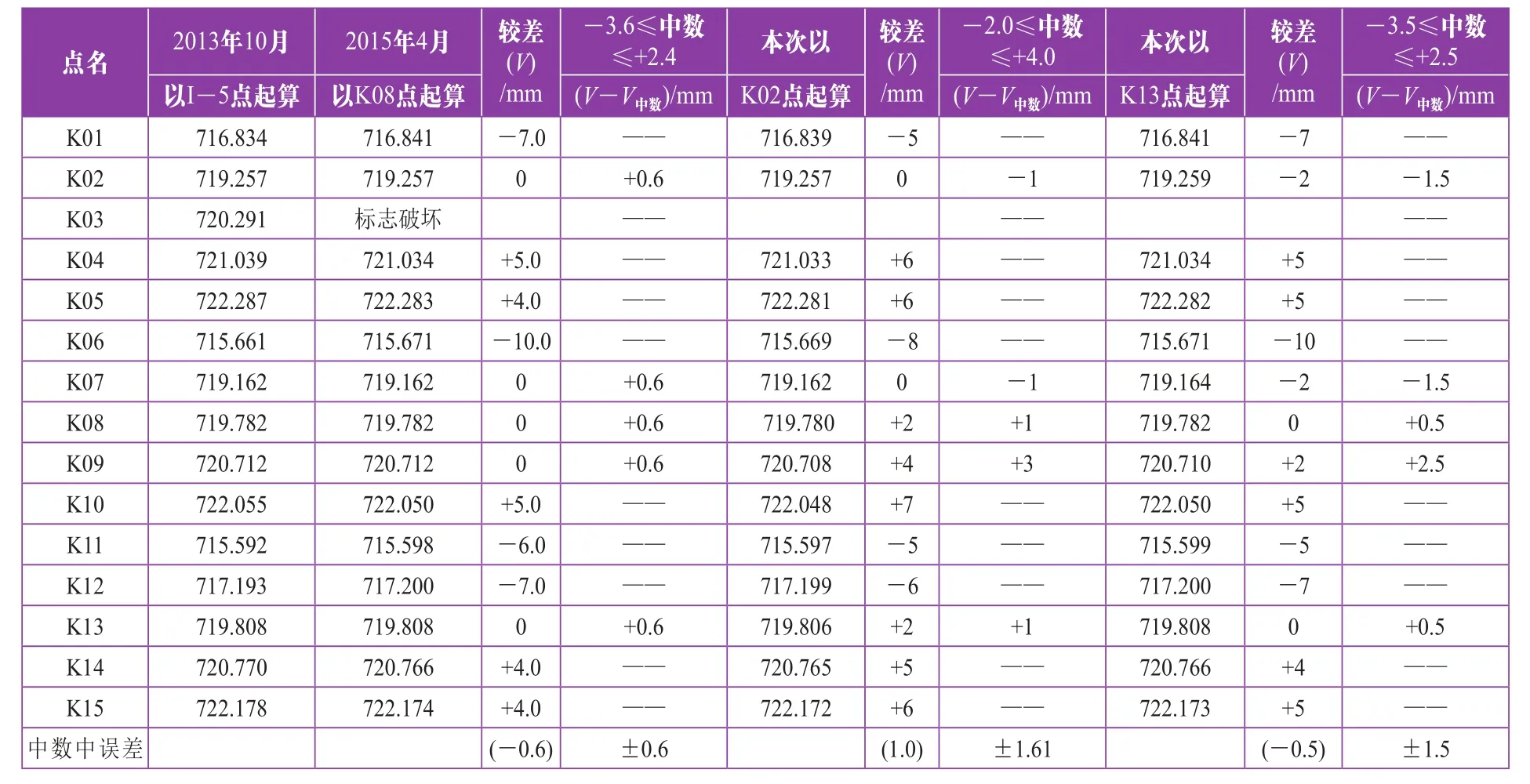
表4 第三类高程较差及高程较差中误差统计
4.1 高程较差计算与统计
以本次选择的起算点为准,按水准线路逐一求出其它各点的高程;再对应点号,用首次的高程值减去本次的高程值,得到该点的高程较差。计算结果见表2、表3、表4。
由表2可知,只依赖前次的成果或随意选择起算点,而未对起算点的高差没有进行检测,结果不能确保起算点的可靠性。例如:随意选用K06或K01再或K12作为起算点,高程较差呈现的是系统性误差,其结果不正确的。
如表3所示,K04~K05测段、K11~K12测段、K14~K15测段高差较差满足技术规程的要求,可以任选用其中的一点作为起算点,但从整个控制网的情况来衡量,起算数据仍不可靠。
(1)如K04~K05测段高差较差满足技术规程的要求,K05~K06测段高差较差不满足技术规程的要求,这时第一选择是满足技术规程要求的K04或K05作为起算点。
(2)又如K11~K12测段高差较差满足技术规程的要求,K12~K13测段高差较差不满足技术规程的要求,这时第一选择是满足技术规程要求的K11或K12作为起算点。
(3)再如K14~K15测段高差较差满足技术规程的要求,K13~K14测段高差较差不满足技术规程的要求,这时第一选择是满足技术规程要求的K14或K15作为起算点。
施工控制网即使进行了检测工作,片面强调某测段高差较差满足技术规程的要求,但起算点不一定可靠。只有用误差理论选取M值最小的点才是最可靠的。
在表2中,以K12为起算点计算的高程较差列中,取高程较差和的中数,本例中数为6.4 mm,对应的起算点应是K13或K08。
如表3中,以K11为起算点计算的高程较差列中,取高程较差和的中数,本例中数为5.6 mm,对应的起算点应是K13或K08。以K08、K02、K13为起算点,计算结果见表4。
在表4第五列、八列、十一列中,只取满足条件[(中数-3 mm)≤高差较差的中数≤(中数+3 mm)]的点进行统计,其余点不进行统计(剔除粗差)。
4.2 距离较差计算与统计
以本次选择的起算点为准,经平差计算,求出各点坐标。采用坐标反算,求出本次起算点到各点的距离。如以K08为起算点,则:

用同样的方法,计算首次K08到各点的距离,计算结果见表5。

表5 距离较差统计
表5为距离较差统计表。本算例平面控制网起算点的可靠性为一次性通过,符合要求,在此不做过多叙述。但衡量起算点可靠性的算法、思路与选择高程起算点是一致的。
5 选取控制点作为起算点频次统计
本算例共6次选择起算点,现将每次与高程较差和的中数最接近的控制点选出,并进行统计,统计结果见表6。

表6 被选为起算点频次统计
由表4、表6统计结果表明,选出K08作为起算点是最佳方案。在表4中,以K08、K02、K13为起算点,计算的高程较差中误差属同一个量级,可靠程度一样。
6 几点说明
6.1 选择起算点和选择可靠点的区别
用高程较差的取值范围进行可靠点筛选,如:(中数-3 mm)≤高程较差的中数≤(中数+3 mm),即满足这个条件的点被选出;而起算点是用高程较差的中数选取的,其结果见表7。

表7 被选为可靠点频次统计
表6共进行了6次计算,选出的起算点和表7每一次选出结果基本一致。可见,用高程较差的取值范围选取可靠点更加快捷方便。
从实际工作角度出发,在表2中,高程较差统计只计算一次,按区间〔(中数-3 mm)≤高程较差的中数≤(中数+3 mm)〕选择可靠点,取4-6个比较合适。
6.2 高程较差取值范围
(1)把高程较差取值范围扩大,如取(中数-5 mm)≤高程较差中数≤(中数+5 mm),则选出的可靠点多,计算工作量增大,但选取最佳起算点的结果是一样的。
(2)把高程较差取值范围缩小,只取最靠近高程较差中数的点,有可能把最佳起算点排除在外,如表6所示,在第四次、第六次选取的过程中,没有选取K08、K13点。虽然计算工作量减小了,但预期目的没有达到。
6.3 高程较差中误差
本文设定的高程较差中误差与实际计算的高程较差中误差比较接近,且计算值小于目标值。
7 结论
(1)采用本方法确认的施工控制网复测起算点可靠性高,能使整个控制网数据前后统一、保证放样数据一致性;可以排除原先复测计算时的随意性和片面性,更重要的是统一认识,杜绝随意性和片面性(高程较差呈现系统误差)计算成果的使用;具有快速寻找到起算点并合理选择点位的优点。不论是高程较差、还是距离较差,只要大于限差的规定,控制点点位就发生了变化,应以本次复测的成果为准。
(2)本方法对沉降观测基准网、变形观测控制网的复测也有借鉴意义。
[1]DL/T 5001-2014,火力发电厂工程测量技术规程[S].
