基于聚类分析多通道InSAR联合相位解缠算法∗

薛永娇,禹卫东

(1.中国科学院电子学研究所,北京100190;2.中国科学院大学,北京100039)

0 引言

干涉合成孔径雷达(Interferometric Synthetic Aperture Radar,InSAR)测量技术是通过从两幅SAR复数据图像中提取的干涉相位差,利用地表高程信息和干涉相位差之间的关系,获取地表三维信息的重要遥感技术[1-2]。传统的单通道InSAR技术相位解缠算法通常要求相邻像素点的相位变化不超过π,即要求高程重建区域具有空间连续性,在地形起伏较大的地区,例如高山、城市等区域,传统单通道InSAR无法有效解决复杂地形高程反演问题[2],并且单通道相位解缠方法运算较为复杂,受噪声影响比较大,存在误差传递现象,因此很难满足实际反演精度的要求。

随着InSAR技术的发展,多通道InSAR测量技术(包括多频率InSAR测量技术[3]和多基线In-SAR测量技术[4])成为目前InSAR技术的研究热点。多频率InSAR测量技术通过使用不同的工作频率或者对SAR信号频谱进行子带分割得到[5],通过载频不同,扩大干涉处理高度模糊数。多基线InSAR测量技术通过在单航过飞行器上设置多个天线或者对同一区域多次航过,得到同一地区不同角度或者不同时间的SAR图像,通过基线不同,扩大干涉处理高度模糊数[6]。模糊高度数的扩大有效解决了高程层叠问题和相位欠采样问题,实现对复杂地形进行相位解缠,得到精确度更高的解缠相位信息[7]。

随着多通道干涉SAR系统的发展,多通道高度重建算法也不断地涌现出来。自从多通道InSAR高程重建算法提出以来,各类方法中最具代表性的算法有:1)基于多通道数据的相位概率统计特性直接进行高程重建,代表算法有多通道最大似然估计(ML)算法[8]和基于Markov随机模型的MRF-MAP算法[9]。ML算法反演精度与工作频率、相干系数以及干涉图数目有很大关系,MRF-MAP算法能够通过利用相邻像素信息提高反演精度,但运算时间长、内存压力大。2)利用多通道InSAR数据的多样性将单通道相位展开算法拓展为多通道相位展开算法,最具代表性的是最小平方法[10]。3)利用不同通道的缠绕相位和对应高度模糊数之间的线性关系进行高程反演。最早在1994年由Xu提出,同时提出中国余数定理(CRT)的多通道相位解缠方法[11],但是该方法存在鲁棒性较差的问题,对噪声非常敏感,所以在实际应用中比较差。2011年,于瀚雯在CRT算法的基础上提出了一种快速聚类的高程重建(CA)方法[6],将具有相同模糊数向量的像素聚为一类,对某一类像素进行相位解缠绕,从而达到降噪和快速相位解缠的目的,然而数据量过大时,由于噪声的积累,像素聚类数目选择对高程反演精度产生很大影响。在CA算法基础上,刘会涛等在2015年提出了密度聚类的改进聚类分析高度重建(CANOPUS)算法[12],利用多通道InSAR缠绕相位的线性组合,作为待聚类数据,充分利用待聚类数据的空变特性,使得聚类精度有所提高、速度加快。

本文针对CA算法噪声鲁棒性差、反演精度较低的问题提出了基于聚类分析的多通道InSAR联合高程重建算法(CARE)。第1节首先介绍基于聚类分析的多通道高程重建算法原理以及该算法存在的问题,第2节详细介绍聚类分析和区域扩展的联合相位解缠算法原理,第3节给出联合高程重建算法在仿真和实测数据集上的重建结果,第4节给出分析和结论。

1 基于聚类分析的InSAR相位解缠算法原理

在多通道的干涉合成孔径雷达系统中,φl为第l通道的缠绕相位值(-π≤φl＜π),ϕl为第l通道的实际相位值,缠绕相位和实际相位之间满足关系:

以双频InSAR系统为例,实际的地形高度h和绝对相位ϕl之间满足关系式:

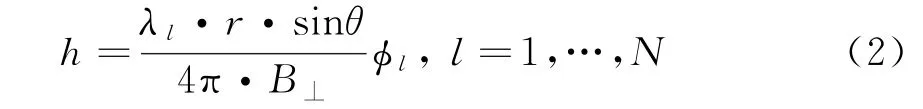
式中,λl为第l通道的波长,B⊥为垂直基线长度,r为主天线到目标的斜距,θ为主天线到目标的斜视角。对于同一观测区域,由式(1)和式(2),可得到双频InSAR系统中缠绕相位和频率的约束关系:

由此,可以得到不同通道波长、模糊数向量和缠绕相位之间的关系为

式中,k,λ和φ分别表示相应通道对应像素模糊数向量、波长和缠绕相位,下标为通道数。由式(4)可知,干涉图中某一像素的信息可以表示成线性方程,其斜率和截距由λ1,λ2,φ1和φ2共同确定。该像素的模糊数向量[k1,k2]是该直线上的整数点。因此,具有相同模糊数向量的所有像素对应同一直线。在低噪情况下,截距存在明显的聚类现象,如图1所示,图1(a)是待聚类数据。

聚类分析算法利用相同模糊数向量的像素具有式(4)中相同截距的特性,将具有相同模糊数向量的像素聚为一类。其算法流程为:

1)获得截距直方图和直方图包络;

2)获得直方图包络峰值,将截距峰值内所有像素归为一类;

3)直方图中峰值点的横坐标作为该类中截距,通过搜索方法获得满足式(4)的[k1,k2],这组[k1,k2]即为该峰值截距对应的模糊数向量,通过式(1)即可获得解缠相位值。

在InSAR图像处理中,数据量大,很容易因为噪声的积累淹没某个聚类中心,导致该类消失,噪声越高,聚类的准确性越不可靠。为了减少噪声积累,本文提出只针对突变地形进行基于聚类分析的多通道相位解缠。

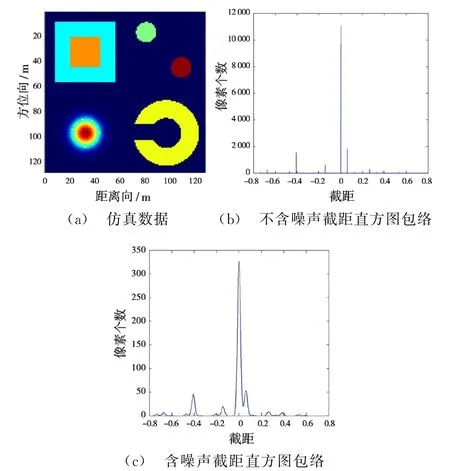
图1 截距直方图包络

2 联合相位解缠算法基本原理

在InSAR相位图中,在地形连续的高相干区域,相邻像素之间的相位变化较小,在随机散射严重或者地形起伏较大的区域,相邻像素之间的相位变化较大,相位产生突变[15]。因为多通道InSAR系统对突变地形解缠精度高,所以本算法通过边缘提取,获得突变地形位置信息。

2.1 边缘提取

干涉相位图中相位跳变明显的区域通过图像边缘检测可以得到十分明显的边缘曲线[14]。在一幅M×N的干涉图中,利用式(4)中截距的空变特性信息,将截距矩阵设为边缘提取矩阵:

为了找到边缘,可以在矩阵ψ中利用一阶或者二阶导数来获取相位变化,从而提取干涉相位图的边缘曲线:

式中,ψm,n∈N(ψi,j),N(ψi,j)为像素点ψi,j的邻域(如4邻域,8邻域)。在InSAR图像中,因为地形复杂导致相位变化不规则,因此,本文利用prewitt算子进行X方向和Y方向边缘提取,利用sobel算子进行对角线方向的边缘提取。prewitt表达式和sobel表达式如下所示:

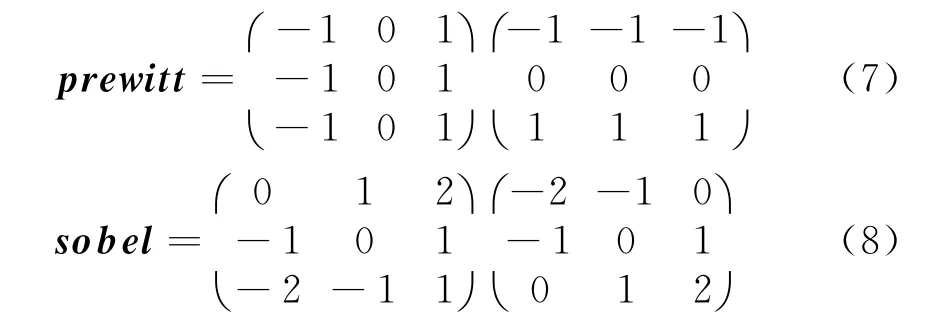
边缘提取后得到的曲线图E′=[e i,j],i∈[0,M-1],j∈[0,N-1],该曲线图对研究突变相位关系时,并不能提供有效信息,因此需要对边缘曲线图进行形态骨架提取。处理后可表示为

式中,skel[]为骨架提取算子,E″为处理后的边缘曲线矩阵。

实际提取得到的并非是某一区域的边缘,而是边缘的轮廓,并不是有效的突变位置信息,所以对检测到的边缘进行二次边缘检测,得到相邻边缘E。E是一个二值矩阵,有效记录了相位突变的位置信息。二次边缘检测也保证了待解缠像素24邻域中有效已解缠像素的个数,提高邻域像素对待解缠像素的影响力,加快区域扩展速度。

为了保证聚类的准确性,本文提出对截距矩阵进行均匀采样,提取的突变数据作为初步待聚类数据。为了进一步降低噪声对聚类准确性的影响,本文将待聚类数据中低相干区域数据剔除,作为最终的待聚类数据集D。然后根据多通道CA相位解缠算法进行相位解缠,得到区域扩展种子像素集S。这样在保证数据多样性的前提下降低数据量,从而降低噪声积累,提高聚类准确性。

2.2 区域扩展相位解缠

区域扩展处理是从种子点开始将其邻域中满足条件的像素合并到同一区域,直到处理完所有相邻像素。InSAR干涉图像中的相位解缠绕过程实际是将像素从“缠绕相位”扩展为“解缠相位”的过程[15]。在CA算法中,即使不会因噪声积累淹没聚类中心,含噪点的解缠相位仍然误差较大,因此本文提出利用数据集D的解缠相位S作为区域扩展种子点。利用区域扩展进行其余像素的相位解缠,按照邻域已经解缠像素的“影响力”大小,选择和估算待解缠像素的相位。

邻域已经解缠像素的“影响力”分为两种:像素距离“影响力”和相位连续性“影响力”。将待解缠像素的24邻域看作5阶矩阵P5×5,8邻域视为3阶矩阵P3×3。P中已解缠像素所在位置值为1,待解缠像素所在位置值为0。设相位梯度矩阵为G3×3,以目标待解缠像素为中心,两个像素的半径中,若某一方向两个像素均解缠,相位梯度矩阵G3×3在该方向的值为1,否则为0。图2中,黑色像素为目标像素,白色像素为未解缠像素,网格和斜线分别表示8邻域已解缠像素和16邻域已解缠像素。将目标像素受到24邻域中已经解缠像素的距离“影响力”和相位连续“影响力”如下:

式中,ω1,ω2,ω3为归一化影响权重系数,且ω1＜ω2＜ω3。当目标像素邻域影响力大于某一阈值,即可对该像素解缠相位进行初步估计。设目标像素24邻域中16邻域和8邻域已经解缠像素的相位矩阵为H5×5和H3×3,则相位的初步估算值为

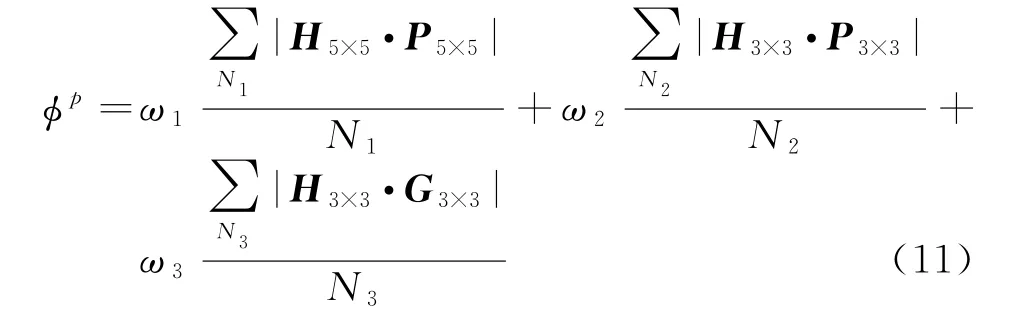
式中,N1,N2,N3分别为矩阵P5×5,P3×3和G3×3中非零值个数。得到的估算解缠相位需要通过可靠性检测。设估算解缠相位预测可靠性参数为d p,是初步估算解缠相位和邻域中解缠相位差值的加权平均值,其表达式如下:

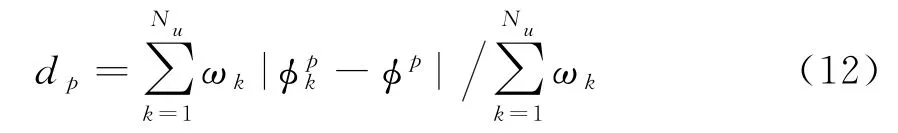
当d p＜π/2时,初步估算模糊数为

估算解缠相位:

这样,对于一些含噪声较大的像素点,估算相位不能通过可靠性检测,可以忽略该像素,继续进行区域扩展,待其周围解缠相位个数增多,估算相位可靠性增大,同时,适当放宽估算可靠性检测条件为d p＜π或者d p＜2π,直到所有像素解缠完成。

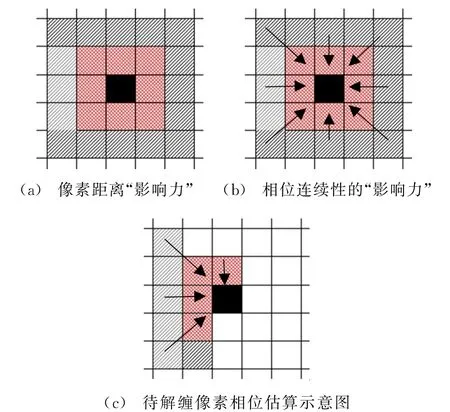
图2 待解缠像素邻域的“影响力”模型

3 实验结果

本文提出的基于聚类分析的多频率联合高程重建算法,通过对仿真数据(128像素×128像素)、基于美国Isolation Peak国家公园的仿真数据(458像素×157像素)和巴塞罗那部分城区多基线InSAR实测数据(96像素×131像素)进行验证。

3.1 仿真数据实验结果

仿真数据建立了一个128行×128列的模拟突变模型。如图3所示,数据表征最大高度为450 m,最大高度差为450 m。高度模糊数分别为42.22 m和57.47 m,相邻两点的最大干涉相位差分别为21.32π和15.66π。表1是仿真数据的主要参数。

表1 基于模拟地形的仿真系统参数

图3(a)为无噪声仿真数据的三维立体图,图3(b)和图3(c)为通道1和通道2对应的含噪声去平地干涉相位图,图像的信噪比为20 dB,图3(d)为截距图,即为CA算法的待聚类数据,图3(e)为通过对待聚类数据进行边缘检测得到的突变地形的位置信息,图3(f)为通过采样和二次边缘检测后得到的本文提出算法的待聚类数据。

图3 仿真数据

下面,通过仿真数据来比较最大似然估计(MLE)相位解缠算法、CA算法及本文算法的性能,如图4所示。

图4 仿真数据高程重建结果

从图4(a)可以看出,最大似然估计(ML)相位解缠结果中存在大量噪点。由图4(b)可以看出,传统CA算法解缠结果较好,但噪点数目仍然不少。图4(c)本文算法相位解缠结果,图4(d)为本文算法得到的高程反演误差,可以看出该算法不仅解缠精度高,而且噪点数目少。算法性能对比如表2所示。

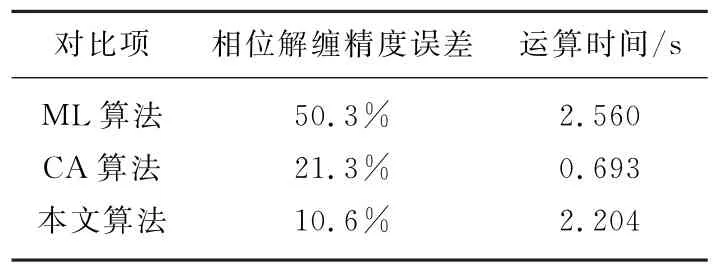
表2 基于模拟地形的算法性能对比

第二个仿真实验采用的是美国Isolation Peak国家公园DEM数据。基于地形的多通道仿真系统频率分别为4.9 GHz和3.6 GHz,干涉数据的相干系数约为0.85,其他参数如表3所示。图5(a)和图5(b)分别是高频和低频数据获得的干涉相位图,图5(c)是截距图,图5(d)是由截距图进行边缘检测得到的突变地形位置数据,图5(e)是经过数据均匀采样和突变检测后得到的待聚类数据。

表3 基于真实地形的仿真系统参数

图6(a)显示了Isolation Peak地形的真实DEM值,图6(b)是最大似然估计算法得到的DEM数据,图6(c)是聚类分析算法得到的DEM数据,图6(d)是本文算法得到的DEM数据,图6(e)是本文算法得到的高程反演误差值。对比图6(c)和图6(d)可以发现,本文算法解缠结果比CA算法解缠结果中噪点明显减少,并且本文算法的误差值要明显小于CA算法。算法性能对比如表4所示。

表4 基于真实地形的算法性能对比

由表2和表4中不同算法相位解缠精度和运算时间对比发现,本文提出算法较CA算法虽然运行时间相比于CA算法要慢,但是解缠精度提高10%,本文算法运行时间和最大似然估计算法时间相当,在提高解缠精度的同时,一定程度上保证了运行效率。

图5 Isolation Peak仿真数据

图6 Isolation Peak数据集高程重建结果

3.2 实测数据实验

实测数据使用的是巴塞罗那部分城区干涉SAR图像。这两幅图像由TerraSAR-X以重复轨道方式获得。两幅干涉图对应的基线长度分别为151.5 m和86.6 m,高度模糊数为36.64 m和64.12 m。图7(a)、图7(b)分别为基线151.5 m和86.6 m对应干涉图。图8(a)为最大似然估计高程重建结果,图8(b)为CA算法高程重建结果,图8(c)为本文提出算法重建结果,图8(d)为本文算法重建后的三维高程图。

图7 不同基线对应Barcelona部分城市区域干涉图

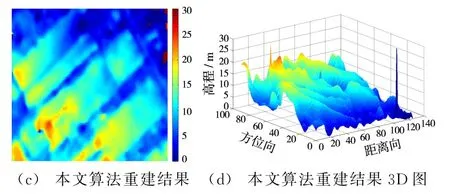
图8 Barcelona实测数据集高程重建结果

4 结束语

本文提出一种联合聚类分析和区域扩展的多通道干涉SAR高程重建算法,聚类分析算法对突变地形解缠精度高,区域扩展相位解缠算法对连续地形细节恢复效果好,本文算法结合两种算法的优点,与传统CA算法相比,通过边缘提取和对数据的均匀采样降低待聚类数据量,减小数据噪声积累。同时,均匀对带聚类数据进行采样,避免了区域扩展算法中噪声的传递,噪声鲁棒性好、相位解缠精度高、计算量适中。该算法适合数据量大、解缠精度要求高的干涉SAR图像相位解缠。但本文算法仍然存在不足,以后工作中,仍然需要对边缘检测和采样获得的待聚类数据进行优化,减少区域扩展种子数据带来的重建误差。

[1]BAMLER R,HARTL P.Topical Review:Synthetic Aperture Radar Interferometry[J].Inverse Problems,1998,14(4):1.

[2]YU H,XING M,BAO Z.A Fast Phase Unwrapping Method for Large-Scale Interferograms[J].IEEE Trans on Geoscience and Remote Sensing,2013,51(7):4240-4248.

[3]PASCAZIO V,SCHIRINZI G.Estimation of Terrain Elevation by Multifrequency Interferometric Wide Band SAR Data[J].IEEE Signal Processing Letters,2001,8(1):7-9.

[4]FERRETTI A,PRATI C,ROCCA F.Multibaseline InSAR DEM Reconstruction:the Wavelet Approach[J].IEEE Trans on Geoscience and Remote Sensing,1999,37(2):705-715.

[5]王伟.多频率InSAR高程信息重建算法研究[D].哈尔滨:哈尔滨工业大学,2006:18-19.

[6]于瀚雯.单/多基线相位解缠绕技术研究[D].西安:西安电子科技大学,2012:75-87.

[7]YU H,LI Z,BAO Z.A Cluster-Analysis-Based Efficient Multibaseline Phase-Unwrapping Algorithm[J].IEEE Trans on Geoscience and Remote Sensing,2011,49(1):478-487.

[8]PASCAZIO V,SCHIRINZI G.Multifrequency In-SAR Height Reconstruction Through Maximum Likelihood Estimation of Local Planes Parameters[J].IEEE Trans on Image Processing,2002,11(12):1478-1489.

[9]FERRAIUOLO G,PASCAZIO V,SCHIRINZI G.Maximum a Posteriori Estimation of Height Profiles in InSAR Imaging[J].IEEE Geoscience and Remote Sensing Letters,2004,1(2):66-70.

[10]靳国旺,张红敏,徐青,等.多波段InSAR差分滤波相位解缠方法[J].测绘学报,2012,41(3):434-440.

[11]YUAN Z,LI F,DENG Y,et al.Multichannel In-SAR DEM Reconstruction Through Closed-Form Robust Chinese Remainder Theorem[J].IEEE Geoscience and Remote Sensing Letters,2013,10(6):1314-1318.

[12]刘会涛,张欢,邢孟道,等.改进的多基线相位解缠绕CANOPUS算法[J].系统工程与电子技术,2015,37(8):1767-1772.

[13]FANG S,MENG L,WANG L,et al.Quality-Guided Phase Unwrapping Algorithm Based on Reliability Evaluation[J].Applied Optics,2011,50(28):5446.

[14]郭春生.优化的区域增长InSAR相位解缠算法[J].中国图象图形学报,2006,11(10):1380-1386.

[15]毕海霞,魏志强.基于区域识别和区域扩展的相位解缠算法[J].电波科学学报,2015,30(2):244-251.