图像配准与角点提取算法研究

徐 静，刘延芳，唐中海

(万博科技职业学院计算机科学技术系，合肥 230031)

0 引言

图像配准是指在不同时间段，对取自不同传感器、不同成像条件下的同一景物的若干图像进行匹配，建立图像之间的对应关系和确定几何变换参数的过程。

1 图像配准的一般方法

一般情况下，根据在配准中所用到图像信息的不同把配准分成：基于灰度的方法、基于变换域的方法和基于特征点的方法等[1]。

1.1 基于图像灰度的方法

这种方法是利用图像中的灰度数据来确定一种比较模板，在待匹配的图像上用比较模板按某种相似性度量顺序来进行搜索获得最佳匹配点。一般采用的函数是SSD(Sum of Squared Difference)，称作灰度差的平方和函数[2]。

(1)

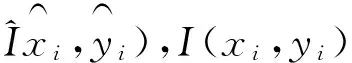
1.2 基于变换域的方法

基于变换域的方法又被称为相位相关法。利用傅里叶变换的原理将图像由空间域变换到频率域来进行图像配准，因此图像上的操作如：平移、镜像、旋转和缩放在傅立叶变换域上都有相应的体现[3]。

1.3 基于特征的方法

基于特征的方法要先提取图像的相关信息，再根据特征点对两幅图像进行匹配，估计出几何变换参数，从而建立两幅图像间的映射。图像特征的分类如下：

1)区域特征。当图像的待配准区域轮廓分割较明显时，则可以考虑使用基于区域的特征匹配，它的优点非常明显：直接选取区域内的灰度值作为匹配信息，所以不需要额外计算。它的局限性是只适用于配准平移变换。

2)边缘特征。图像的边缘是比较直观的，一般来说，边缘特征的计算量比区域匹配更少。所以具有更高的实时性。但是边缘特征也存在着一些不足：比如它要求图像本身有着较为明显的形状轮廓，利用边缘的搜索策略复杂度较高等。

3)点特征。通过角点这个特征元素，可以迅速掌握对象的外部轮廓，因此它在图像匹配和目标识别等方面有十分重要的作用。特征点分为狭义特征点和广义特征点[4]。狭义特征点具有一般意义上的常规属性，而广义上的特征点一般用封闭曲线或范围的重心点代表分割点。

2 基于SUSAN角点匹配算法

2.1 SUSAN算法原理

它的基本原理是：以简单的二值图像为例，中间的像素点为核子，以核子为圆点做一个圆形区域，像素点所在区域被称为USAN，是SUSAN算法的模版[5]。当核心位于一条直线边缘附近时(即模板b)，USAN面积区域就会减少；当核心恰好位于直线边缘上时(即模板c)，USAN面积减半。当核心恰好位于角点上时(即模板e)，USAN面积最小。USAN面积大小决定了该点是特征点的可能性，其越小则是特征点的可能性就越大[6]。

图1 SUSAN圆形模板

图2 图像上不同位置的圆型模板

2.2 算法描述

用模板对整幅图像进行扫描，再与给定的阈值来比较灰度值，从而判断它是否属于USAN区域，如式(2)：

(2)

式中：C(r，r0)为判别函数，判断点是否属于USAN区域；(r，r0)为模板某点的位置坐标；I(r0)为模板核心像素点的灰度值；I(r)为任意某像素点的灰度值；t为给定的阈值。

USAN中像素点的个数可以用式(3)求得：

(3)

式中s(r)就是表示在所选定区域内像素点的个数。

2.3 SUSAN算法特点

SUSAN算法对于直线和曲线的边缘检测的效果都比较好，而且不需要计算导数。缺点是很难检出弱边缘上的角点，当灰度差异较小时，很容易遗漏掉角点。此外角点定位精度不够高，容易出现角点漂移和错检的情况[7]。

2.4 SUSAN算法实验结果

图3是应用SUSAN算法对室内外图进行角点提取的效果图，对图像边缘的直线和曲线检测的效果都比较好。SUSAN算法无需梯度运算，保证了算法的效率。

(a)室内图

(b)室外图图3 SUSAN算子角点特征图

3 基于Moravec角点匹配算法

3.1 Moravec算法简介

它的思想是：以像素为中心，先取一个m×m的窗口(如图4所示的5×5窗口)，获得每个像素的兴趣值(interest value)，计算0°、45°、90°和135° 4个方向的灰度差平方和，取其中的最小值，再设定一个阈值去遍历，筛选出候选角点。

图4 5×5窗口

3.2 Moravec算法特点

该算法的优点是运算速度快，对边缘角点敏感，但也存在一些问题：1)由于只考虑4个方向，具有方向上的局限性；2)由于没有降噪，所以该算法虽然速度快但抗噪表现不佳。

3.3 Moravec算法实验结果

图5是应用Moravec算法对室外图进行角点提取的效果图。由于Moravec算法过于简单，所以轻易就可以看出图中有一些明显的特征点没被检测出来，并出现了一些伪角点，需要后期进行筛选。

(a)室内图

(b)室外图图5 Moravec算子角点特征图

4 基于Harris角点匹配算法

4.1 Harris算法简介

C.Harris和M J.Stephens[8]于1988年提出了基于Moravec算法的Harris角点检测算法，该算法认为，特征点是一定域值范围内的兴趣值筛选出的最大像素点的集合。实际操作中，可以依次取出每个像素的邻域中的若干个像素，从中心像素和这几个像素中提出最大值。如果中心点像素的兴趣值就是最大值，则该点就是特征点[9]。

其数学描述为式(4)：

(4)

式中：E为亮度变化的值；(u，v)为特征点在x，y方向的平移量；w(x，y)为滤波窗口函数；I(x，y)为图像在(x，y)的亮度；M为2×2的对称矩阵。

进行泰勒展开后得到：

(5)

式中IxIy分别为所取的点在水平和垂直方向上的导数。将M相似对角化后得到：

(6)

式中：λ1和λ2为矩阵M的特征值，每个像素对应着一个矩阵；Q为旋转因子。

图6中划分了3个区域，分别是：“flat”region，“edge”region，“corner”region[10-11]。通过对矩阵M的两个特征值的分析，可以得出：

1)如果两特征值都很小，意味着窗口所处区域灰度近似常量，可以任意方向移动，函数E发生很小的改变，如图6中的“flat”region；

2)如果一个特征值很大，而另一个特征值很小时，表现成屋脊状。沿着边缘方向移动使得函数E变化很小，如图6中的“edge”region；

3)如果两个特征值都很大，表现成尖峰状，沿任意方向的移动都将使得E急剧增大，如图6中的“corner”region。

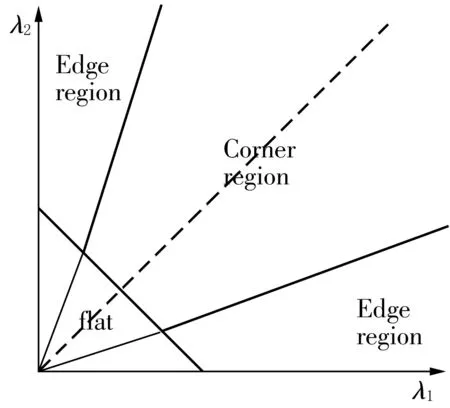
图6 Harris角点检测示意图

4.2 Harris算法特点

Harris算子是一种非常有效的角点检测算法，一般来说有以下几个方面的优点：

1)自动化程度较高：Harris算子操作简单，在运算过程中只用到图像灰度的一阶差分以及滤波。因不需设置阈值所以自动化程度高。

2)角点提取较为均匀：在图像纹理信息较丰富的区域部分用Harris算法可以提取出比较多的有用的角点，反之则较少。

3)提取出的角点较稳定：当图像存在旋转、灰度变化时，对Harris算法提取出来的角点影响不大。

4.3 Harris算法实验结果

从图7中可以看出，Harris提取的角点分布均匀，而且Harris算子的抗噪能力比SUSAN算子强。此外Harris算法是各向同性的，所以在检测角点的过程中不会因为图像旋转移动等外部环境的变化而变化。另外，Harris是用一阶偏导数描述图像的亮度变化的，角点检测结果基本不受光强影响[12-13]。

(a)室内图

(b)室外图图7 Harris算子角点特征图

5 几种算法性能比较

在进行图像匹配之前，需要检测出角点具有以下性质：一是即使在不同视角范围中，仍然能准确定位在图像中同一空间范围的特征点的位置；二是特征点周围区域的信息丰富，所以特征点能够快速准确地去匹配。

在图像检测领域，角点是比较直观并且重要的一个特征，是掌握图像轮廓特征的重要因素。在实际应用中，各种角点检测方法各有特点，主要从以下两个方面去衡量它们的可操作性：首先是匹配的准确性。在角点提取过程中，不可避免地有噪声等干扰，可能出现误操作和漏提取，要尽量避免。其次是要保证角点在同场景中不同图像上的一致性。

本文采用基于匹配支持度的松弛匹配算法对几种算法的匹配正确率进行了比较。比较结果见表1。

表1 匹配正确率的比较

再对原始图像加入了不同程度的噪声干扰，利用上述算法得出噪声对不同算子的影响，比较结果见表2。

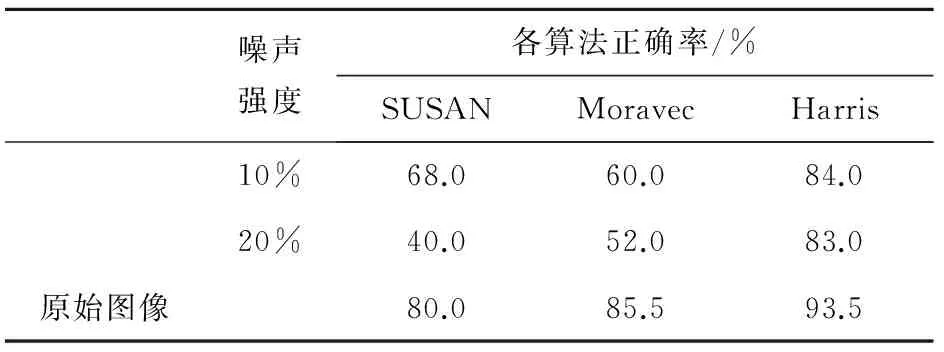
表2 抗噪声效果比较

通过分析得出：Harris算子具有较明显的优势：计算量小，计算过程不需要设置阈值，自动化程度高，提取的角点分布比较均匀，且抗干扰能力强。

6 结语

本文较详细地分析了Maravec、SUSAN和Harris这3种图像特征提取角点检测算法，在此基础上，从匹配正确率和抗噪声效果等方面对此3种算法进行了分析比较，最后确定了Harris算法具有抗干扰能力强、精度高、稳定性好、鲁棒性高等优点。

[1] Ranades，Rosenfeld A.Point pattern matchingby by relaxation[J].Pattern Recognition，1980，12(4):269.

[2] Ton J，Jaln A K.Registering landsat images by point matching[J].IEEE Trans.On Geoscience and Remote Sensing，1989，27(5):642-651.

[3] Huttenlocher D P，Klanderman G A，Rucklidge W J.Comparing images using the Hausdorffdistance[J].IEEE Trans on Pattern Analysis and Machine Intelligence，1993，15(9)：850-863.

[4] Goshtasby A，Stockman G C，Page C V.A region based approach to digital imageregistration witll subpixel accuracy[J].IEEE Trans on Geoscience and Remote Sensing，1986，24(3):390-399.

[5] 王蕾.图像配准技术及应用研究[D].西安：西安电子科技大学，2007.

[6] 谢东海.改进Harris算子用于点特征的精确定位[J].测绘信息与工程，2003，28(2):22-23.

[7] 李红梅，黄梦涛，田爱玲，等.亚像素级标定角点提取新算法[J].西安科技大学学报，2006，26(4):536-540.

[8] Harris C G，Stephens M J.A combined comer and edge detector[C]//Processings of The Fourth Alvey Vision Conference.Manchester，UK：s.n.，1988:147-151.

[9] 管海燕.常用图像边缘检测算子定位精度对比研究[J].测绘与空间地理信息，2005，12(1):36-40.

[10] 张迁，刘政凯，庞咽龙，等.基于SUSAN算法的航空影响的自动配准[J].测绘学报，2005，32(3):245-250.

[11] 程中林，王永国，刘平.一种改进的低照度视频增强方法[J].山东理工大学学报：自然科学版，2010，24(4):98-101.

[12] 覃征.鲍复民.李爱国，等.数字图像融合[M].西安：西安交通大学出版社，2004.

[13] Szeliski R.Video mosaics for virtual environments[J].Computer Graphics and Application，1996，16(2):22-30.