插齿机接刀杆的结构分析与优化
2018-01-19邓志华
杨 涛 邓志华
(武汉交通职业学院,湖北 武汉 430065)
随着制造业的发展,工业上对制齿机床的精度要求越来越高,制齿机床的生产中,插齿机是一个重要的组成部分,插齿的基本原理为用形状为齿轮或齿条的插齿刀具与被加工齿轮按一定的速比作啮合运动的同时,刀具沿齿宽方向做往复运动切削,即展成加工。插齿机接刀杆的生产由厂商自行设计和制造,机床的制造者在机床床身的设计分析、接刀杆的结构设计等方面已做出了大量的研究[1,2],但作为连接刀具和机床的载体,机床的设计者一般只是从接刀杆的材料、硬度、刚度、安装的同轴度等方面对其进行校核,而并未形成系统、完整的设计体系和标准,目前也尚未见文献在此方面进行详细研究。事实上,接刀杆的结构及其安装精度是机床是否合格的重要指标,尤其是在切削时,巨大的切削力矩以及冲击作用下,一旦接刀杆发生变形,导致装刀架轴线弯曲,进而使刀具安装位置产生偏差,将严重影响齿轮的加工质量。为此,本文以某型号直齿插齿机为对象,针对其接刀杆现有结构及安装精度的问题,对其结构进行了分析,给出了优化建议,也为今后其他型号的插齿机开发设计提供支持。
1 现有接刀杆的安装及精度调节方法
1.1 现有接刀杆的结构
如图1所示,为某型号直齿插齿机的刀架示意图,接刀杆一端与机床的刀架体相连,一端与插齿刀相连,刀轴上下运动切削的同时,蜗轮蜗杆带动刀轴作旋转运动。
接刀杆的尾部采用莫式4号锥度与主轴内孔配合,接触面积达锥面面积85%以上,刀具通过另一端的紧刀螺母固定。安装时其端面与主轴端面留有少量间隙便于调整精度,弥补装刀架的制造误差。由于该间距,若接刀杆刚度不够,切削时产生的切削力矩可使其端面变形,导致装刀架轴线弯曲,进而使刀具安装位置产生偏差,影响机床加工精度。
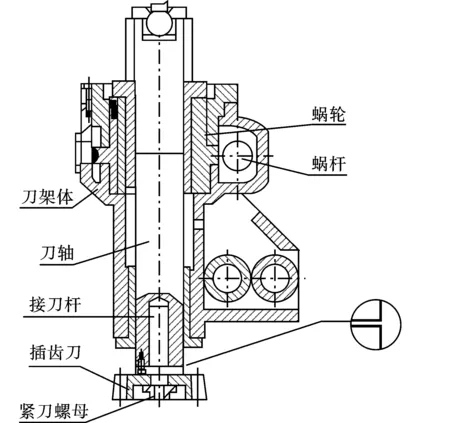
图 1 刀架结构简图
1.2 安装精度调节方法
如图2所示,接刀杆盘状部分上的四个沉孔用来将接刀杆固定在主轴上,插齿刀通过紧刀螺母固定在圆形突台上。主轴调整至与工作台垂直后装上接刀杆,一边旋转主轴,一边在接刀杆端面上打表测量端面跳动误差,调节四个螺母的松紧来平衡跳动误差。此举是使接刀杆发生形变达到
精度要求。同理,由于切削时的切削力,接刀杆也可能发生形变影响精度。初步推测切削时变形大部分都发生在直径为85“厚度D=15”的圆盘部分,厚度的大小对变形影响最大,故对“D=15”尺寸进行优化。
2 确定切削力
开始分析之前需计算插齿时的最大切削力,根据插齿最大切削力计算公式[3]:
Fzmax=∑AmaxP
Fzmax——最大切削力
P——单位切削力
∑Amax——最大切削总面积
m——工件模数(mm)
z——工件齿数
fc——圆周进给量(mm/dst)
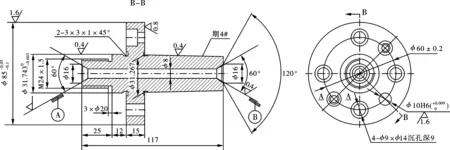
图 2 接刀杆零件图
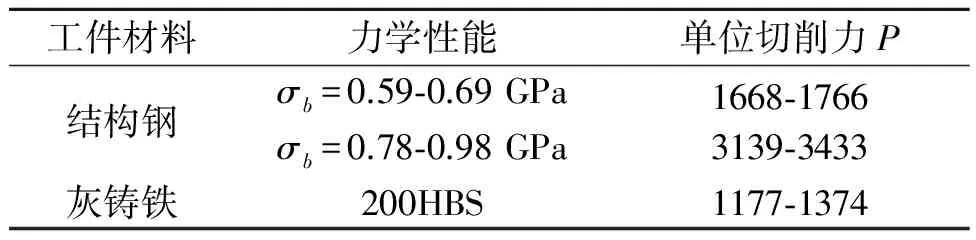
工件材料力学性能单位切削力P结构钢σb=0.59⁃0.69GPaσb=0.78⁃0.98GPa1668⁃17663139⁃3433灰铸铁200HBS1177⁃1374
模拟以圆周进给量为0.5,加工3模50齿,材料为结构钢的齿轮,得出最大切削力为6118.1 N。
3 建立有限元模型及求解
分析最大切削力时刻的形变为静力分析,插齿过程中可认为刀具不发生形变,主要研究接刀杆的形变,故可将刀具视为刚体,刀具与接刀杆之间可视为“刚-柔”接触,在此分析中刀具充当传递载荷的作用。
本文选取的插齿机加工范围为:公称直径100mm、m=1-6mm、α=20°,根据GB 6081—2001《直齿插齿刀基本型式和尺寸》中的标准要求,本文在进行有限元分析时,以“公称直径100mm、m=1-6mm、α=20°”系列中的模数3mm的插齿刀参数,建立插齿刀的几何模型。
由于插齿刀和接刀杆分别设置材料属性,独立划分网格,接触面共享节点。接刀杆在UG中建模,设定图2中“D=15”为参数变量,设定参数变量名为“ds_D”,使Ansysworkbench内置的参数过滤器识别变量,建立好装配模型后双向导入,在DM模块勾选参数“ds_D”作为输入变量。插齿刀和接刀杆的接触面在螺纹连接的预紧力和形变下产生摩擦力,且形变时会有微量分离,故接触面性质设定为摩擦接触,设定滑动摩擦系数为0.17,为非线性接触。刀具刚度较大,定义为刚体并将相关面设定为目标面,接刀杆面为接触面。接刀杆为旋转体,为了划分网格更方便,建模时省略了螺纹特征,采用多重区域网格划分[4]。对于刀具的接触面采用三角网格,划分网格后的模型如图3。
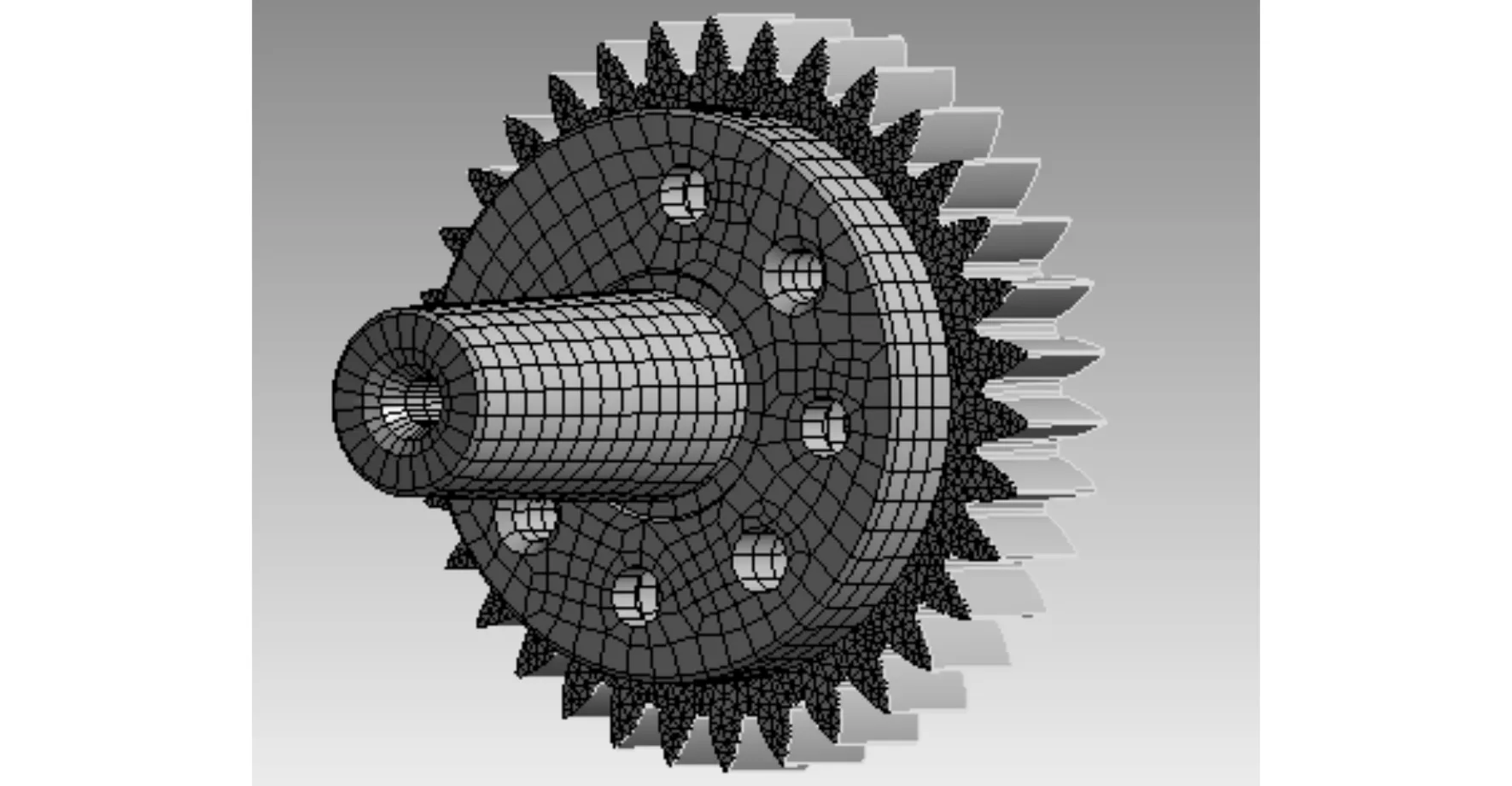
图 3 划分网格后的模型
将接刀杆锥面施加固定约束,并对插齿刀单个齿廓底面施加竖直向上的载荷。在计算结果中插入应力与整体变形,勾选这两项结果的最大值作为输出变量,求解后得到如图4与图5整体变形云图。

图 4 接刀杆应力云图
可以看出应力与形变都与接刀杆轴线大致对称,其中切削力所在的一边应力较大,应力最大的部位位于接刀杆锥面底部,增大锥面底部的直径和圆滑过渡拐角会对应力有所改善,但对于同一型号插齿机而言,其主轴直径固定,接刀杆锥面底部直径无法再有过多调整空间,故可通过调节接刀杆圆盘部分的厚度来分析是否会对应力大小有所改善。

图 5 整体形变
而整体形变最大的部位位于切削力所在的插齿刀刀尖,由于插齿刀圆盘部分的变形,导致插齿刀相对于原来位置的整体偏移量与刀具直径成正相关。这一偏移量直接影响了插齿精度。可见在插齿时,除了减小切削力以外,若选用直径较小的刀具亦有助于改善加工精度。
4 优化分析
基于之前的结果对接刀杆进行优化,在Workbench项目视图中插入“Response Surface”,插入过程笔者不在此赘述[5]。进入DOE中设定输入参数“ds_D”的下边界值13上边界值为18,当前值为15,并插入并行参数图表。选择更新项目数据,系统会在参数边界内自动选取点进行计算。因为一次计算多个参数,此次计算过程会比较长,求解完后进入DOE查看数据如表2和图6。
表2中A列为系统给定的设计点序号,B列为设计点的数值,C和D列内为每个设计点对应的最大应力与最大整体形变,可以看到,从13-18mm选取了五个设计点,并分别计算除了这五个设计点对应的最大应力和最大总体变形;图6中P5为设计点尺寸,P6为最大应力,P7为最大整体变形量。我们选出最大变形量最小、最大应力最小、和最大变形量与应力都相对较小的三个设计点,为图中4号、3号、1号和2号线条。对于5号线条,其变形量与应力都较大,故舍弃。4号线条整体形变最小,但应力最大,3号线条应力最小,但整体变形最大,都不宜作为最佳设计点。1号线条整体变形较小,应力较大,2号线条整体变形较大,应力较小。由于最大变形量为主要研究对象,故综合考虑选取1号线条,即设计点值为15.5mm。此时最大变形为0.038892mm,最大应力为216.35MPa,较优化前的最大变形0.050255,最大应力224.51MPa,分别下降了22.6%和3.7%,说明将接刀杆连接圆盘的厚度增加至15.5mm,可以较好地增加接刀杆的整体刚度,避免由于接刀杆变形、偏斜等造成的加工质量变差。
表2输入参数与输入变量表格
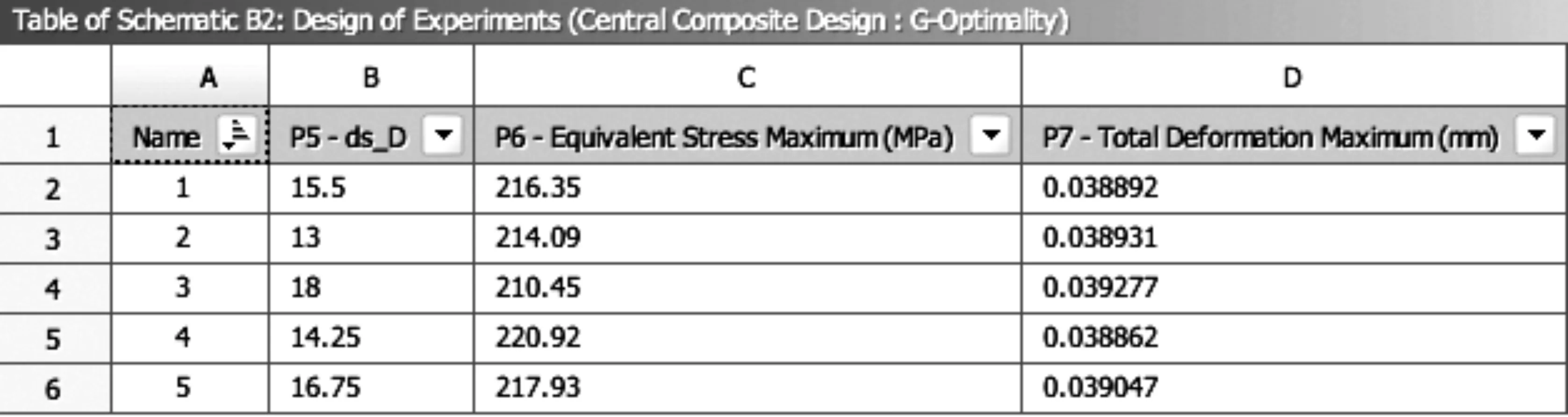
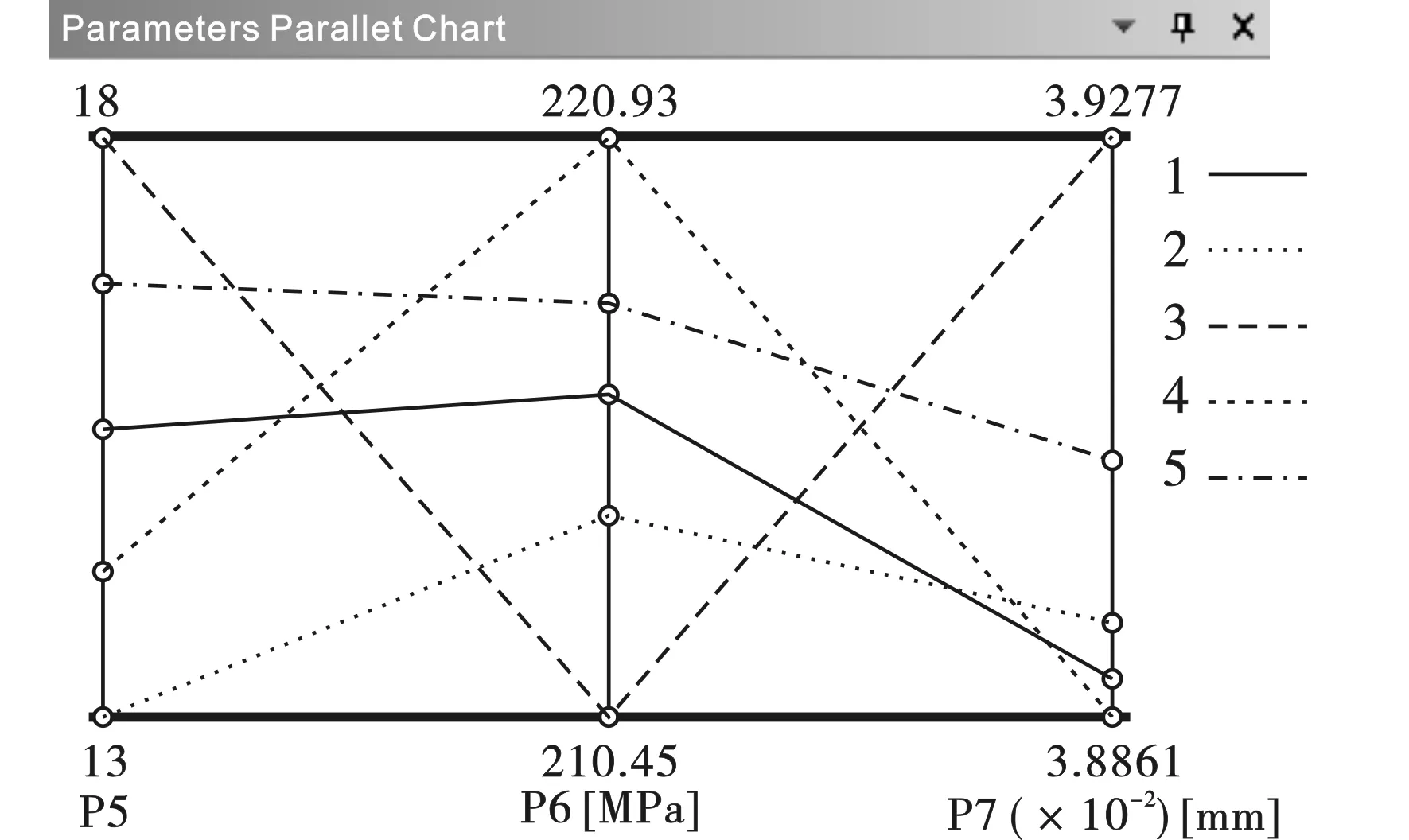
图 6 并行参数图
5 结论
(1)利用Ansys Workbench分析出接刀杆加工时的变形分布及应力分布,结果表明插齿刀的直径对接刀杆的整体变形有较大影响,同时接刀杆圆盘部分的厚度对应力和整体变形都有明显影响。
(2)在插齿机主轴直径固定,接刀杆锥面底部直径无法再有过多调整空间的条件下,调节接刀杆圆盘部分的厚度,对于接刀杆的受力变形、内部应力状态等,可有一定的调节作用。
(3)以整体变形小为优化目标,应力较小为参考对象,计算分析了不同圆盘厚度条件下,接刀杆的应力和变形状态,优选出圆盘的厚度尺寸,使整体变形和应力都较小。
(4)本文在优化时所给出的边界较小,优化区域也较小。尽管如此,依照文中所给出的方法和流程,增大边界、选取更多模数的插齿刀,亦能计算出最优设计点。后续可开展接刀杆优化后的插齿机实际加工和对比试验,验证优化结果的有效性,并进一步提高优化的效果。
[1]田启华,周祥曼,杜义贤,等.YKS5120B-3数控插齿机床身结构有限元分析[J].机械设计与研究,2010,26(3):53-56.
[2]代国辉,严红毅.数控插齿机新型刀架结构设计[J].制造技术与机床,2013(5):40-40.
[3]杨叔子.机械加工工艺师手册[M].北京:机械工业出版社,2002:1304.
[4]许京荆.ANSYS 13.0 Workbench数值模拟技术[M].北京:中国水利水电出版社,2012:93-97.
[5]李兵,何正嘉,陈雪峰.ANSYS Workbench设计、仿真与优化[M].北京:清华大学出版社,2013:96-98.
