股票配资的收益与风险控制模型

吴红英， 朱 萱， 杨 令

1 股票配资合同

2015年6月，一条“长沙股民4倍配资、全仓中车，两天赔光跳楼”的消息，让股民无法平静，拥有天使和魔鬼双重血统的场外配资要了他的命.从技术层面来说，投资失败导致跳楼的关键原因是对配资炒股这种高回报、高风险投资行为缺乏正确的评估和风险管理技能.炒股的目的一般有风险对冲、套利机会和投机，显然跳楼投资人是典型的投机者，风险管理尤为重要.精确的风险管理需要较为复杂的数学工具和较高的计算手段.

设r，σ，δ分别为股票价格的无风险利率、市场波动率和分红强度，则股票价格St服从随机微分方程（SDE）

其中Wt为标准Brownian运动.假定股民自己出资q，再从配资公司借贷kq买入一支股票，其股价正好为S=（1+k）q，此时配资率（杠杆率）为1∶k.股民与配资公司订立4项合同条款：（1）借贷利率为γ，合同到期日为T，当前日期记为0.（2）如果在[0，T]时间内，股票价格降至kqeγt，股票自动平仓，股民资金全部亏损，配资公司收回本金与利息kqeγt.（3）如果在[0，T]时间内，股票价格升至μq，股票自动平仓，配资公司收回本金与利息kqeγt，股民资金收益为 μq-kqeγt-q=（μ-1）q-kqeγt.这里总是假定 μq＞kqeγt+q，设定 μ 的初衷是防范估计被高估的风险，当股价高到一定程度时及时退市.（4）在到期日，配资公司收回本金与利息kqeγt，股民收入为ST-kqeγt.

杠杆炒股具有股票借贷的某些特征[1，2]，也具有期权的一些基本要素[3-6]，本文采用随机分析和Black-Scholes-Merton偏微分方程来建模，同时设计有限差分格式求解，同时给出数值算例进行必要的讨论.

2 配资收益与风险模型

首先考虑收益状况.股民在到期日的收益支付可以看作股票看涨期权收益，即 h（T，ST）=（ST-kqeγt-q）+，（·）+表示取正部函数，而股民在任意t时刻的贴现收益期望为

在 Black-Scholes-Merton 分析框架上（见文献[3，4]），股民收益期望 V（t，St=S）满足偏微分方程（PDE）

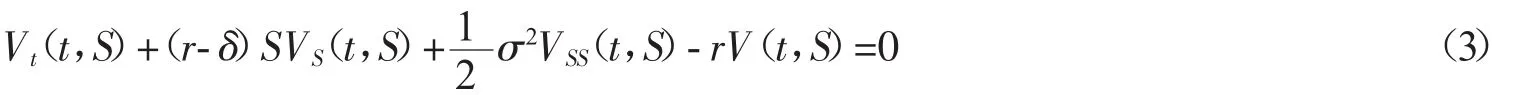
这里S为哑变量，不再是时间的函数.同时加上终端条件

考虑到合同条款（2）（3），我们必须加上边界条件

PDEs（3）（4）（5）和（6）构成所谓的欧式看涨障碍期权.

再来讨论风险度量.股民在到期日的风险支付可以看作股票看跌期权收益，即h~（T，ST）=（q+kqeγt-ST）+，而股民在任意t时刻的贴现风险期望为

与收益分析类似，股票风险期望V（t，St=S）满足PDE

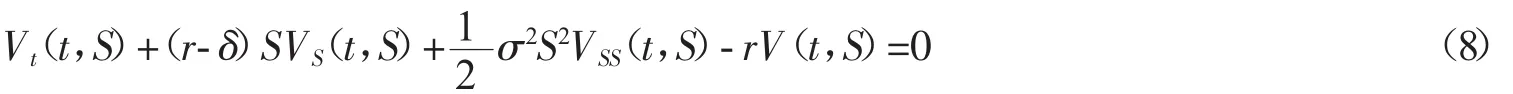
和终端条件

考虑到合同条款（2）（3），我们同样加上边界条件

PDEs（8）（9）（10）和（11）构成所谓的欧式看跌障碍期权.

已知零时刻股票价格S0并给定配资率k，股民投入资金数量，此时股民收益率R、风险率R和风险收益比λ可分别定义为

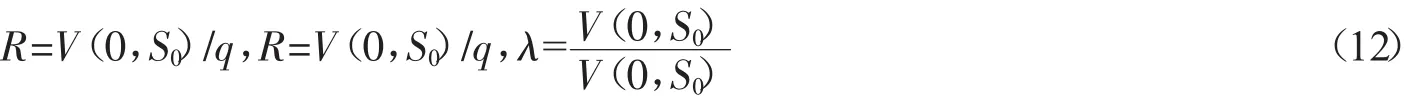
R，R和λ都是无量纲的，R表示单位投入的收益，R表示单位投入的风险，λ则表示单位收益所面临的风险大小.R，R和λ对配资率k较为敏感，同时与借贷利率γ有关，应该是股民最为关注的数量指标.

计算收益期望的PDE（3）-（6）可用有限差分方法来求解.定义固定时间网格

和移动空间网格

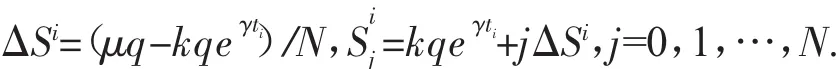
运用中心差分的隐式格式离散PDE（3）得到

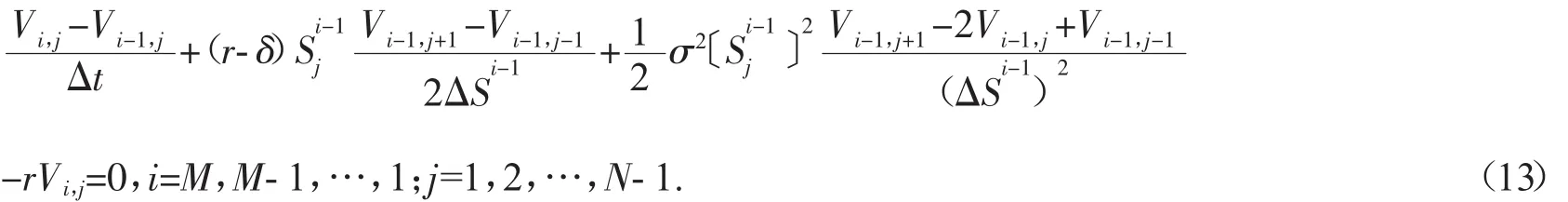
其中 Vi，j为 Vi，j在时间层 Vi-1上的插值函数.对离散系统（13）进行整理，依次关于时间节点 i=M，M-1，…，1 有

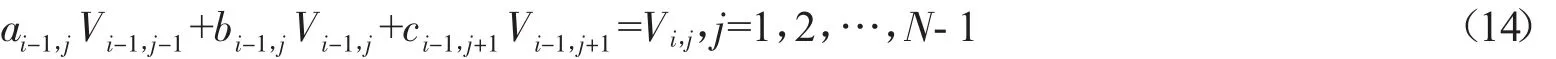
其中

加上终端条件和边界条件

线性方程组（14）可按时间反向演化求解.同理计算风险期望的PDE（8）-（11）也可用有限差分方法来求解，方法类似，这里不再赘述.

表1 不同配资率对收益和风险的影响

3 数值模拟与分析

取无风险利率r=0.05（年利率），股价波动率σ=0.5，初始股价S0=10（元），借贷利率γ=0.07，到期时间T=1（年），其它参数为q=S0/（1+k），μ=6，M=1000，N=1000.

表1列出了有限差分方法的部分计算结果.从表中看到，随着配资率k的增加，单位资本的收益（R）先增后降；在较低配资水平下确实能增加股民期望收益，这正是股民涉足场外配资炒股的动力所在；但在较高配资水平下，由于面临高额借贷利息，股民期望收益必然受损.同时我们也看到，随着配资率k的增加，单位资本的风险（R）先增后降；高配资高风险不难理解；配资水平达到一定程度以后，股民投入很少，风险自然会减低，其余风险已经转嫁给配资公司.单位收益所面临的风险λ总是在提高，这说明风险增长速度快于收益增长速度.另外从表中我们也能看到高收益高风险的投资特征.

从以上分析看出，本文提出的股票配资模型基本体现了借贷炒股的主要特征，实际数值计算结果能够给出股民最为关心的数量指标，具有很强的实用价值.

[1]X.P.Lu and E.R.M.Putri.Semi-analytic valuation of stock loans with finite maturity[J].Commun Nonlinear Sci Numer Simulat，2015，27：206-215.

[2]X.P.Lu and E.R.M.Putri.Fintiematurity margin call stock loans[J].Operations Research Letters，2016，44：12-18.

[3]S.E.Shreve.Stochastic Calculus for Finance I：the Binomial Asset Pricing Model[M].New York：Springer，2003.

[4]S.E.Shreve.Stochastic calculusfor finance II：Continuous-Timemodels[M].Springer Press，2004.

[5]Z.Zhou and X.Gao.Numerical Methodsfor Pricing American Optionswith Time Fractional PDEModels[J].Mathematical Problemsin Engineering，2016：ID 5614950（8 pages）.

[6]Z.Zhou and J.Ma.Lattice Boltzmann methodsfor solving PDEsof exotic option pricing[J].Front.Math.China，2016，11：237-254.