非自治动力系统中的平均跟踪

易 鹏， 吴红英

1 引言与预备知识

就我们所知，对于非自治动力系统的研究，始于20世纪60年代，起步比较晚，其理论也不像自治动力系统那么完善和丰富.近年来，许多自治动力系统的性质被放在非自治动力系统的框架内研究.在文献[1]中，作者研究了非自治动力系统中弱混合和混沌性质.在文献[5-7]中，作者研究了非自治动力系统中混沌性质.在文献[3]中，作者定义和研究了非自治动力系统中的扩张，跟踪和拓扑稳定性质.本文研究非自治的半离散动力系统的跟踪性质.我们用Z+表示非负整数.下面给出本文所涉及的一些概念，有关概念可参见文[1-9]等.设（X，ρ）是一个度量空间.对每一个n∈Z+，令 fn∶X→X 是一个连续映射，其中 f0=id（x）.我们称F={fn}∞n=0是X上的一个时间变化的映射簇.称（X，F）是一个时间变化非自治的半离散动力系统（或者简称动力系统）.对每一个 n∈Z+，我们记 Fn=fn·fn-1·…·f0.

设 A⊂X.用 A 表示｜A｜的基数；用 d（A）表示 A 的密度，用d（A）表示A的上密度，d（A）表示A的下密度.设（X，F）是一个动力系统，其 δ＞0 中 F=.给定，称X中序列是F的一条δ-伪轨，如果对任意 n∈Z+，有

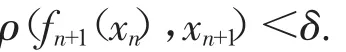
设 x=x0，x1，x2，…，xn=y 为 X 中的有限序列，如果对每一个i∈{0，1，…，n-1}，有ρ（fi+1（xi），xi+1）＜δ，则称x0，x1，x2，…，xn是一条从 x到 y长度为 n 的 F 的 δ- 链（δ-伪轨可以看做无限长的δ-链）.如果对任意的x，y∈X，δ＞0，存在一条从x到y的F的δ-链，则称F是链传递的.

本文主要结果为：若（X，F）和（Y，G）具有平均跟踪性质，则（X×Y，F×G）具有平均跟踪性质（见定理2.4）；系统（X，F）有平均跟踪性质当且仅当对任何q∈[0，1），（X，F）有 q- 平均跟踪性质（见定理 3.2）；具有0-平均跟踪性质的系统（X，F）是链传递的（见定理 3.5）.

2 平均跟踪

接下来我们给出平均跟踪性质在非自治系统上的定义.

定义2.1 设（X，F）是一个动力系统.称X中的一个序列是F的一条δ-平均伪轨，是指存在一个正整数N，使得对任意的n≥N和任意的k∈Z+，都有

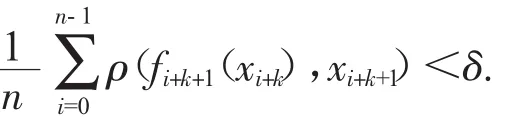
定义2.2 设（X，F）是一个动力系统.称映射F（或系统（X，F））有平均跟踪性质，是指对任意的ε＞0，存在一个δ＞0，使得对F的每一条δ-平均伪轨ξ=这时，也称点z，ε-平均跟踪ξ.

下面的引理来自于文献[9].

引理2.3 令ck是非负的实数列.给定正整数t，令 Ct，n是{k＜n：ck≥t}的基数，即 Ct，n=|{k＜n：ck≥t}|.

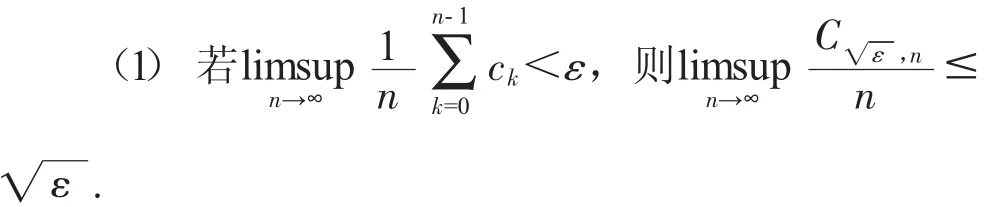
（2）若 ck是以 D为界且

定理 2.4 设（X，F）和（Y，G）是两个动力系统，其中（X，ρ1）和（Y，ρ2）为两个度量空间，F={fn}∞n=0和G=分别是（X，ρ1）和（Y，ρ2）上的一个时间变化的映射簇.若F和G都有平均跟踪性质，则F×G也有平均跟踪性质.

证明 由于ρ1和ρ2分别是X和Y上的度量.取X×Y 上度量为：ρ，对任意 x=（x1，y1），y=（x2，y2）∈X×Y，ρ（x，y）=max{ρ（1x1，x2），ρ（2y1，y2）}.令D=max{ρ（x，y），x，y∈X×Y}和

由于F和G具有平均跟踪性质.对σ＞0，存在δ＞0，使得对每一条F的δ-平均伪轨和每一条G的δ-平均伪轨，分别存在X中的点和Y中的点σ-平均跟踪之.设是X×Y的一条δ-平均伪轨，易知分别是F和G的一条δ-平均伪轨，因此存在点u∈X和v~∈X，使得

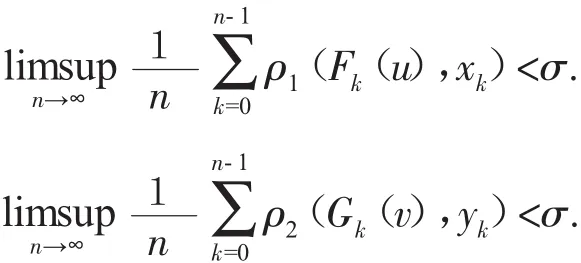
记 ck=ρ1（Fk（u），xk），dk=ρ2（Gk（v），yk），mk=max{ck，dk}，Ct，n=|{k＜n∶ck≥t}|，Dt，n=|{k＜n∶dk≥t}|，

Mt，n=|{k＜n∶mk≥t}|.

易知 Mt，n≤Ct，n+Dt，n.

由引理 2.3（1），知

＜ε

因此F×G具有平均跟踪性质.

3 q-平均跟踪

定义 3.1 设（X，F）是一个动力系统.q∈[0，1）.称映射F（或系统（X，F））具有q-平均跟踪性质，是指对任意的ε＞0，存在一个δ＞0，使得对F的每一条δ-平均伪轨，存在点 z∈X，满足

这时，也称点z，ε-q-平均跟踪ξ.

定理3.2 设（X，F）是一个动力系统.则下列条件等价：

（1）F具有平均跟踪性质；

（2）对任何的q∈[0，1），F具有q-平均跟踪性质.

证明 （1）⇒（2）.取定 q∈[0，1）.对任意 ε＞0，令γ=（1-q）ε.由 F 具有平均跟踪性质，故存在 δ＞0，对 F的任意一条δ-平均伪轨，存在点 z∈X，γ- 平均跟踪之.令A={i∈Z+∶ρ（F（iz），x）i＜ε}.则有

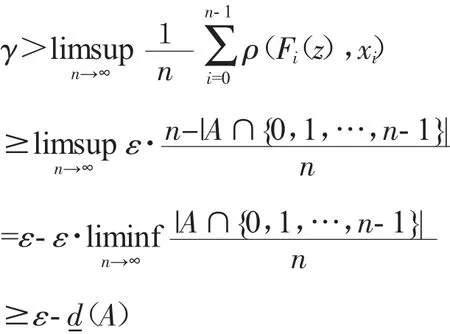
又 γ=（1-q）ε，从而 d（A）＞q.于是 F 具有 q- 平均跟踪性质.

（2）⇒（1）.不失一般性，设 diamX=1.任意取定ε∈（0，1），取.由于F具有q-平均跟踪性质，则存在η＞0，对F的每一条η-平均伪轨ξ=，存在点-平均跟踪之.令

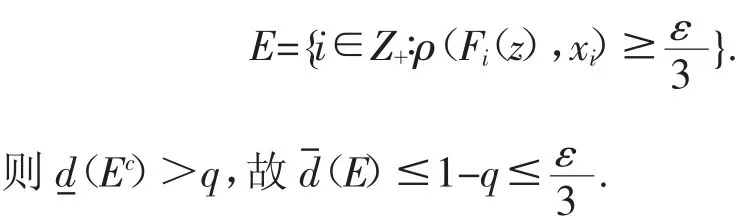
令 En=E∩{0，1，…，n-1}，故

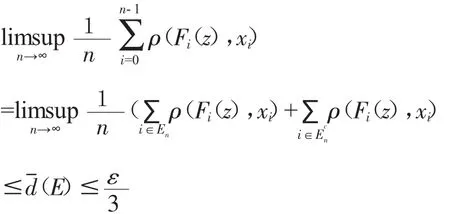
＜ε

于是具有平均跟踪性质.

定理3.3 设（X，F）是一个动力系统，其中F是一个时间变化的映射簇.则下列条件等价：

（1）F具有平均跟踪性质.

（2）对任意的 ε＞0，存在 δ＞0，对F的每一条 δ-平均伪轨，存在点z∈X，满足

证明 （1）⇒（2）.由于F有平均跟踪性质，则对任意的ε＞0，存在δ＞0，使得对F的每一条δ-平均伪轨，能够被点 z∈X，ε2- 平均跟踪之.即

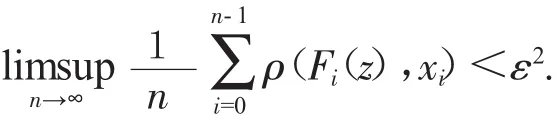
令E={i∈Z+∶ρ（Fi（z），xi）≥ε}，则有

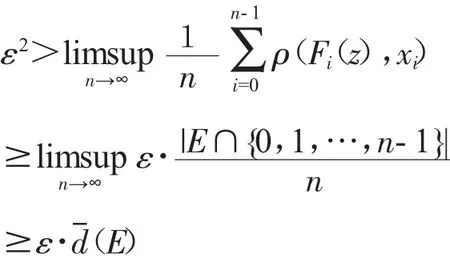
故 d（E）＜ε，所以（2）成立.

（2）⇒（1）.不失一般性，我们设 diamX=1.根据（2），对＞0，存在 δ＞0，对F的每一条 δ-平均伪轨，存在点 z∈X，满足

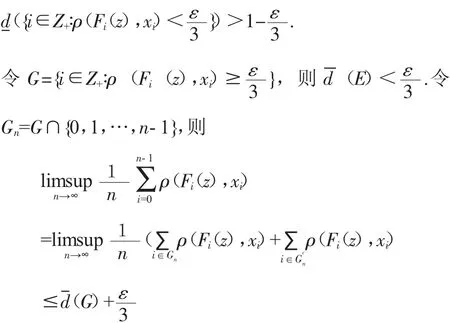
＜ε

故（1）成立.

引理 3.4 设 E，F⊂Z+.若 d（E）=1 且 d（F）＞0，则d（E∩F）＞0.

证明 不失一般性，我们假定diamX=1.任取ε＞0，和任取 x，y∈X.设 δ＞0和 ε＞0满足 0-平均跟踪性质的定义的两个参数.令n0≥2，并且满足＜δ.对任意的 i∈N，令 ni=i!·n0.

下面我们定义一组序列：

…

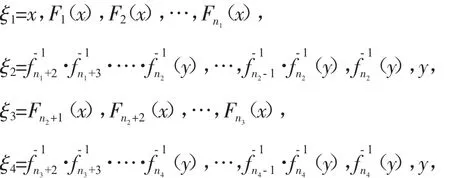
因此，ξ是F的一条δ-平均伪轨.于是存在点z∈X，使得

d（{i∈Z+∶ρ（Fi（z），xi）＜ε}）＞0.

令 M1=[0，n1]∪[n2+1，n3]∪[n4+1，n5]∪…=[0，n1]∪[n2k+1，n2k+1].d（M1）=1，令 M2=Z+M1，则 d（M2）=1.

令E={i∈Z+∶ρ（Fi（z），xi）＜ε}.由于F有0-跟踪性质.故d（E）＞0，则d（E∩M1）＞0，d（E∩M2）＞0.（由引理3.4）

我们能够找到正整数 r∈E∩M1，s∈E∩M2，并且r＜s-1，使得下面的式子成立

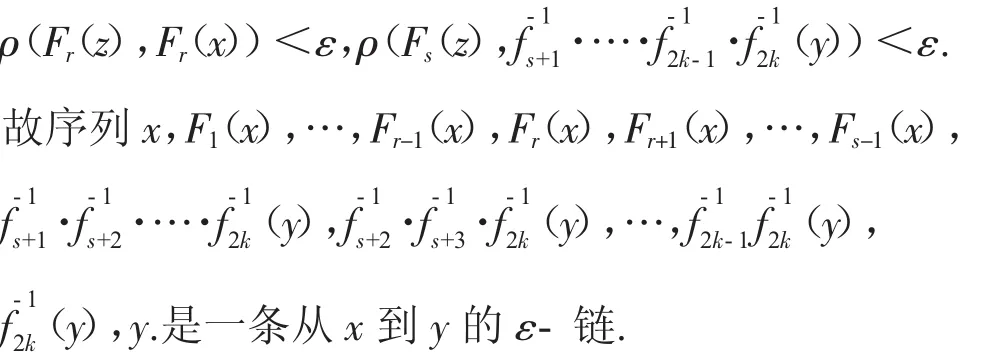
[1]F.Balibrea，P.Oprocha.Weak mixing and chaos in nonautonomous discrete systems[J].Applied Mathematics Letters，2012（25）：1135-1141.

[2]David Richeson，Jim Wiseman.Chain recurrence rates and topological entropy[J].Topology and its Applications，2008（156）：251-261.

[3]Dhaval Thakkar，Ruchi Das.Topological stability of a sequence of mapson a compact metric space[J].Bull.Math.Sci，2014（4）：99-111.

[4]S.Kolyada，L'.Snoha.Topological entropy of nonautonomous dynamical systems[J].Random and Computational Dynamics，1996（4）：205-233.

[5]Qiuling Huang，Yuming Shi，Lijuan zhang.Sensitivity of nonautonomous discrete dynamical systems[J].Applied Mathematics Letters，2015（39）：31-34.

[6]Y.Shi，G.Chen.Chaos of time-varying discrete dynamical systems[J].Journal of Diference Equations and Applications，2009（15）：429-449.

[7]X.Wu and P.Zhu.Chaos in a class of non-autonomous discrete systems[J].Applied Mathematics Letters，2013（26）：431-436.

[8]Yingxuan Niu.The average-shadowing property and strong ergodicity[J].Journal of Mathematical Analysis and Applications，2011（376）：528-534.

[9]Wang H Y，Zeng P.Partial shadowing of average-pseudo-orbits（in Chinese）[J].Sci Sin Math，2016（46）：781-792.