广义内射环的扩张

向跃明

1 引言

在文献[1]中，Page和周引入了环与模的AP-内射性和AGP-内射性的概念.环R称为左AP-内射环，如果对任意 0≠a∈R，aR 是 rRlR（a）的直和项；环R是左AGP-内射环，如果对任意0≠a∈R，存在n＞0使得an≠0且anR是rRlR（an）的直和项.在左AP-内射环与左AGP-内射环两类环上得到了许多左P-内射环的结果.之后，周在文献[2]中继续研究了带各种链条件的左AP-内射环与左AGP-内射环.本文研究AP-内射环和AGP内射环的各种扩张.证明了矩阵环Mn（R）是左AGP-内射环，则R是左AP-内射.因此，作为一个左AGP-内射环不是Morita不变量.此外，我们还证明了如果R的平凡扩张是左AGP-内射，则R是左AP-内射.最后考虑了R[D；C]的左AP-内射性.

本文中R表示有单位元的结合环，所有模都是酉模，J=J（R）是R的Jacbson根.如果X是R的一个子集，X在R中的右零化子（左零化子）记作rR（X）（lR（X））.对于通常的符号参考文献[3]和[4].

2 主要结论

我们首先有如下引理.

引理2.1 如果R是左AGP-内射环，则eRe也是左AGP-内射环，其中e2＝e∈R使得ReR=R.

证明：令 S=eRe，0≠a∈S.则存在 n≥1 使得 an≠0且rRlR（an）=anR⊕Xan这里Xan是R的右理想.由1-e∈lR（an）可知对任意 t∈Xan有（1-e）t=0，这推出.于是eanRe∩eXane=0.显然eanRe⊆rSlS（an），由eanR=anR，

现在我们证明另外一个包含关系.不妨设x∈rSlS（an），记 1＝aiebi，其中 ai，bi∈R.于是对任意 y∈lR（an）和任意 i，有 ebiyean=ebiyan=0.这推出对任意 i，有ebiyex=0.

rSlS（an）=eanRe⊕eXane=anS⊕Xane，这里Xane是S的右理想.故S是左AGP-内射环.

注2.2 引理2.1中的条件ReR=R是必需的.例如，设R是域F上的矩阵代数，有如下形式

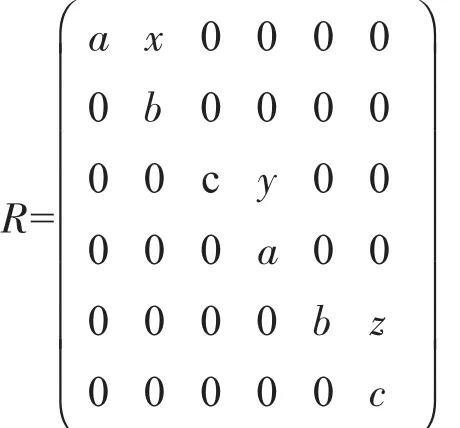
由文献 [5]的例子9，R是QF-环，于是R是左AGP-内射环.

设e=E11+E22+E44+E55矩阵单位的和.则e是R的幂等元且有ReR≠R和）.我们证明S不是左 AGP-内射环.事实上）.于是选因此不存在S的右理想XS使得rSlS（琢）=琢S⊕XS.

推论2.3 如果R是左AP-内射环，则对任意满足条件ReR=R的幂等元e，eRe也是左AP-内射环.

我们现在探讨矩阵环Mn（R）是左AGP-内射环的充分和必要条件.记矩阵单位为 Eij，1≤i，j≤n.

引理2.4设S=Mn（R），a∈R.则下述等价：

（1）rSlS（aE1n）=（aE1n）S⊕XS，这里XS是S的右理想；

（2）rRlR（a）=aR⊕XR，这里XR是R的右理想.

证明：（1）⇒（2）对任意 b∈rRlR（a），lR（a）⊆lR（b）.如果（cij）∈lS（aE1n），则ci1a=0，i=1，…，n，于是ci1∈lR（a）⊆lR（b），推出ci1b=0，i=1，…，n，这证明了（cij）（bE1n）=0.因此lS（aE1n）⊆lS（bE1n），进而bE1n∈rSlS（aE1n）=（aE1n）S⊕XS.记bE1n=（aE1n）（cij）+（dij），其中（cij）∈S，（dij）∈XS，则b=acnn+d1n∈aR+XR，这里XR={d|dE1n∈XS}.假设 c∈aR∩XR，则 c=ar，r∈R.于是 cE1n=（aE1n）（rEnn）∈（aE1n）S∩XS=0，这推出 c=0.故 rRlR（a）⊆aR⊕XR.现在需要证明XR⊆rRlR（a）.对任意x∈XR，有xE1n∈XS⊆rSlS（aE1n）.对任意y∈lR（a），有（yE11）（aE1n）＝0，于是yE11∈lS（aE1n）.因此（yE11）（xE1n）＝0.这推出yx=0，即有x∈rRlR（a）.所以aR⊕XR⊆rRlR（a）.

（2）⇒（1）如果B=（bij）∈rSlS（aE1n），则lS（aE1n）⊆lS（B）.对任意j≠1，Eij（aE1n）=0，因此EijB=0，这证明了=0 对 k=1，2，…，n，bjk因此如果 b∈lR（a），则bE11∈lS（aE1n）⊆lS（B），因此b∈lR（b1j），j=1，…，n.故lR（a）⊆lR（b1j），这推出b1j∈rRlR（a）=aR⊕XR.不妨记 b1j=ac1j+e1j，其中 c1j∈R，e1j∈XR.

定理 2.5 如果Mn（R）（n≥2）是左 AGP-内射环，则R是左AP-内射环.

证明：对任意0≠a2∈R，设U=aE1n.由Mn（R）左AGP-内射环，故存在m＞0，使得Um≠0且rSlS（Um）=（Um）S⊕XS，这里 XS是 S 的右理想.然而 U2=0，故 rSlS（U）=US⊕XS.根据引理2.4，存在R的子集XR使得rRlR（a）=aR⊕XS.因此R是左AP-内射环.

推论2.6 设R是环.则下述等价：

（1）Mn（R）是左AGP-内射环（n≥1）；

（2）Mn（R）是左AP-内射环（n≥1）；

（3）HomR（Rn，R）是 HomR（I，R）的直和项，这里 I是Rn的任意n-生成子模.

证明：（2）⇒（1）是显然的.

（1）⇒（2）由假设，对n≥1，M2（Mn（R））≅M2n（R）是左AGP-内射环.由定理2.5，Mn（R）是左AP-内射环.

（2）⇒（3）由[1]中推论 3.9可得.

注2.7 设K是域，L是K的子域且ρ：K→L是一个同构.例如，令K=F（y1，y2，….），这里F是域，ρ（yi）=yi+1，ρ（c）=c，c∈F.设 K[x1，x2；ρ]是 K 上的扰多项式环，其中对任意 k∈K 和 i=1，2 有 kxi=xiρ（k）.记 R=K[x1，x2；ρ]/（x21，x2

2）.根据文献[6]中例子 1 和命题 2，R 是左AGP-内射环但不是左AP-内射环，于是由定理2.5，Mn（R）不是左AGP-内射环n＞1.因此环的左AGP-内射性不是Morita不变量.

设R是环，M是R上的双模.R在M上的平凡扩张R∝M={（a，x）|a∈R，x∈M}，加法定义为分量分别相加，乘法定义为（a，x）（b，y）=（ab，ay+bx）.为简便起见，我们记I∝X={（a，x）|a∈I，x∈X}，这里I是R的子集，X是M的子集.

下列结论是文献[7]中命题3.1的对偶情况.

引理2.8 设R是环，对任意a∈R，Xa是R的右理想，T=R∝R.则下述等价：

（1）rRlR（a）=aR⊕Xa；

（2）rTlT（0，a）=（0，a）T⊕X（0，a），其中X（0，a）=0⊕Xa是T的右理想；

（3）rTlT（a，0）=（a，0）T⊕X（a，0），其中X（a，0）=Xa⊕0是T的右理想；

（4）rTlT（a，a）=（a，a）T⊕X（a，a），其中X（a，a）=Xa⊕Xa是T的右理想.

命题2.9 设R是环.如果R∝R是左AGP-内射环，则R是左AP-内射环.

证明：令 T=R∝R.对任意 0≠a∈R，（0，a）2=0.由假设，存在T的右理想X（0，a）使得rSlS（0，a）=（0，a）S⊕X（0，a）.对任意（b，c）∈rSlS（0，a），有lS（0，a）⊆lS（b，c）.因为（0，1）∈lS（0，a），0=（0，1）（b，c）=（0，b），这证明b=0.如果（m，n）∈（0，a）S，则 m=0.因此 X（0，a）=0⊕Xa，其中Xa是R的右理想.由引理2.8，我们有rRlR（a）=aR⊕Xa，这证明了R是左AP-内射环.

注2.10 值得注意的是：R是左AGP-内射环不一定能推出T=R∝R是左AGP-内射环.例如，令R是注2.7中的环.假设T=R∝R是AGP-内射环，则根据命题2.9，R是AP-内射环，矛盾.

设D是环，C是D的子环，1c∈D.我们记

R[D，C]={（d1，…dn，c，c…）|di∈D，c∈C，n≥1}其中的加法（乘法）定义为相应的分量分别相加（相乘）.自从 Nicholson 在文献[8]中利用 R[D，C]构造半正则环不是正则环的例子，越来越多的代数学者使用这种结构构造各种反例（见[9]，[10]）.

下列引理由零化子的性质显而易见.

引理2.11 设D是环，C是D的子环.则对任意rDlD（a）⊆rDlC（a）且 rClD（a）⊆rClC（a）.

定理2.12 设D是环，C是D的子环，1c∈D.则下述等价：

（1）R[D，C]是左 AP-内射环；

（2）D 是左 AP-内射环且对任意 a∈C，C∩（aD⊕X）a⊆aC⊕X′a，其中Xa⊆rDl（Da），X′a⊆rCl（Da）.

证明：（1）⇒（2）记 S=R[D，C].我们首先证明 D 是左 AP-内射环.对任意 d∈D，令 d=（d，0，0，…）∈S.由S是左AP-内射环，rSlS（d）=dS⊕Xd¯，其中Xd¯⊆rSlS（d）是S的右理想.对任意a∈rDlD（d），记a=（a，0，0，…）∈S.设 y=（y1，…，ym，y，y，…）∈lS（d），则有 yd=0，于是y1d=0，进而y1a=0，这推出ya=0.因此a∈rSlS（d）=dS⊕Xd¯，进而a∈dD⊕Xd，这里Xd={x∈D|（x，0，0，…）∈Xd¯}.故 rDlD（d）⊆dD⊕Xd. 反之对任意 γ∈Xd，γ=（γ，0，0，…）∈Xd⊆rSlS（d）.任取b∈lD（d），b=（b，0，0，…）∈S，有bd=0，因此bγ=0，这推出bγ=0，即b∈rDlD（d），故有Xd⊆rDlD（d），所以 dD+Xd⊆rDlD（d）.现令 m∈dD∩Xd，则有 m=dd′，d′∈D 且 m=（m，0，0，…）∈Xd¯.故有 m∈dS∩Xd¯=0，这推出 m=0.我们证明了 rDlD（d）=dD⊕Xd.因此D是左AP-内射环.

现设 x∈C∩（aD⊕X）a，其中 a∈C，Xa⊆rDl（Da），则 x=ad+k，k∈Xa.令 x=（x，x，…），a=（a，a，…）∈S.对任意y=（y1，…，ym，y，y，…）∈l（Sa），我们有yi∈lD（a）（i=1，…，m），y∈l（Ca）.由引理2.11，yix=y（iad+k）=yiad+yik=0，yx=yad+yk=0.这推出 yx=0.因为 S 是左 AP-内射环，x∈rSl（Sa）=aS⊕Xa¯，进而x=ac+l，c∈C，l∈X′a，其中X′a={l∈C（|l，l，…）.如果n∈aC∩X′a，则 n=ac，c∈C.令 n=（n，n，…）∈S，因此 n∈aC∩Xa¯=0，推出n=0.所以有 C∩（aD⊕X）a⊆aC⊕X′a.对任意 h∈X′a，h=（h，h，…）∈Xa¯⊆rSl（Sa）.如果g∈l（Da），则g=（g，g，…）∈l（Sa），因此gh=0，进而gh=0.于是h∈rClD（a），这推出⊆rCl（Da）.

（2）⇒（1）任取 a=（a1，…，am，a，a，…）∈S，设 b=（b1，…，bn，b，b，…）∈rSl（Sa）.我们不妨令n≥m.对任意xi∈l（Da）i，i=1，…，m，记xi=（0，…，0，xi，0，…，0），这里xi是第 i个分量. 则 xi∈lS（a），进而 xib=0，这推出xib=0，i=1，…，m.因为D是左AP-内射环，bi∈rDl（Da）i=aiD⊕Xai，i=1，…，m，其中Xai⊆rDl（Da）i是D的右理想.类似地，我们有 bj∈rDl（Da）=aD⊕Xa，j=m+1，…，n，其中Xa⊆rDl（Da）是D的右理想.b∈rDl（Da）=aD⊕Xa.因此b∈C∩（aD⊕X）a⊆aC⊕X′a.由假设，X′a⊆rCl（Da），这推出 b∈aS+Xa¯，其中

对任意 x=（x1，…，xn，x，x，…）∈Xa¯和 z=（z1，…，zk，z，z，…）∈l（Sa）（k≥n），我们有ziai=0（i=1，…，m）；zja=0（j=m+1，…，k）；za=0.因此 zixi=0（i=1，…，m）；zjxj=0（j=m+1，…，n）；zj′x=0（j′=n+1，…，k）；zx=0，这证明了 zx=0，进而x∈rSl（Sa），于是有Xa¯⊆rSl（Sa）.如果x=（x1，…，xn，x，x，…）∈aS∩Xa¯，则 xi∈aiD∩Xai=0（i=1，…，m）；xj∈aD∩Xa=0（j=m+1，…，n）且 x∈aC∩X′a=0，故rSl（Sa）=aS⊕

所以S左AP-内射环.

引理2.13 设D是环，C是D的子环，1c∈D.如果 C 是左 AP-内射环，则对任意 a∈C，C∩（aD⊕I）⊆aC⊕I′，其中I⊆rDl（Da），I′⊆rCl（Ca）.

证明：若 x∈C∩（aD⊕I）.则 x=ad+γ，这里 d∈D，γ∈I⊆rDl（Da）.任取y∈l（Ca），由引理2.11γ∈rDl（Da）⊆rDl（Ca）.故yx=y（ad+γ）=yad+y＝0.我们得l（Ca）⊆l（Cx）.又由C是左AP-内射环，故x∈rCl（Ca）＝aC⊕I′，其中I′⊆rCl（Ca）.所以C∩（aD⊕I）⊆aC⊕I′.

根据定理2.12和引理2.13我们有：

推论2.14 设D是环，C是D的子环，1c∈D.如果C和D都是左AP-内射环，且对任意a∈C，rCl（Ca）⊆rCl（Da），则R[D；C]是左AP-内射环.

注2.15 推论2.14的逆命题不成立.例如，设T=R[D；C]，其中 D=Z∝，C＝Z∝0.可知 C≅Z 不是 AP-内射环.由文献[10]中例子28的讨论，T是FP-内射环，因此T是AP-内射环.

[1]PAGESS，ZHOUY Q.Generalizations of principally injective rings[J].J.Algebra，1998，206（2）：706-721.

[2]ZHOUYQ.Ringsin which certain right ideals aredirect summandsof annihilators[J].J.Aust.Math.Soc.，2002，73（2）：335-346.

[3]ANDERSONFW，FULLERKR.Ringsand Categoriesof Modules[M].New York：Springer-Verlag，1974.

[4]LAMTY.Lectures on Modulesand Rings[M].New York：Springer-Verlag，1999.

[5]KOIKEK.Dual rings and cogenerator rings[J].Math.J.Okayama Univ.，1995，37：99-103.

[6]CHENJL，ZHOUY Q.GP-injectiveringsneed not be P-injective[J].Comm.Algebra，2005，33（7）：2395-2402.

[7]XIANGYM.Almostprincipally small injectiverings[J].J.Korean Math.Soc.，2011，48（6）：1189-1201.

[8]NICHOLSONWK.Semiregular Modulesand Rings[J].Can J.Math，1976，33（5）：1105-1120.

[9]CHENJL，LIY L，ZHOUYQ.Constructing Morphic Rings[J].Advancein Ring Theory，World Scientific，2005：26-32.

[10]CHENJL，ZHOUY Q.Extensionsof injectivity and coherent rings[J].Comm.Algebra，2006，34（2）：275-288.