叠加法求均匀带电球体电场问题
2018-01-19郭泓昊张雅男李庆芳
郭泓昊 张雅男 李庆芳
(南京信息工程大学,江苏 南京 210044)
大学物理在静电场章节中,先是讲解了点电荷的电场强度计算方法,然后利用场强叠加原理先后求出均匀带电圆环、均匀带电圆盘等电荷均匀分布的带电体轴线上的电场分布。而对于均匀带电球体的电场分布,一般是在讲解过静电场中的高斯定理后,利用高斯定理来求解。因为利用高斯定理求解均匀带电球体的电场无论从物理概念还是计算方面都是简单易懂的。课堂上求解均匀带电圆环轴线上一点的电场强度,是将其分解为无数个电荷微元,求每个电荷微元在轴线上的电场矢量和,求解均匀带电圆盘轴线上电场强度也是相同的方法[1-3]。学过该方法后,有的同学想利用这种方法求解均匀带电球体外的场强分布却得到了错误结果,但各种教材中没有给出相关的推导。查阅了若干文献,虽然也介绍了求解方法,但这些方法都是先求出圆盘的电势,然后利用电势梯度求出场强分布[4-6]。这种方法是静电场章节最后的知识点,而且还要利用泰勒展开来讨论电场分布。对于初学静电场知识的同学,有一定的难度,理解上也不如电荷微元叠加方法简单。为此,本文作者根据自己的理解,将符号函数引入均匀带电圆盘电场计算公式,然后利用该公式,根据电场叠加原来推导出均匀带电球体的电场分布。虽然数学计算略微复杂,但物理概念清晰,有利于同学理解微元法在物理中的应用。
1 叠加法求解均匀带电球体场强
大学物理教材中对于求解均匀带电球体在空间中产生的静电场,一般是利用高斯定理求解[3]。已知球体半径为R,电荷体密度为ρ,与球心距离为r的场点处,其电场强度大小为
(1)
大学物理课本中,在讲解高斯定理求解电场强度之前,是利用对电荷微元在场点的电场强度求矢量和来计算不同带电体的电场[3]。笔者并不满足于直接由高斯定理求解均匀带电球体在空间中产生的场强大小,也利用上述方法计算均匀带电球体产生的电场,计算过程如下。
如图1所示,以球心为坐标原点建立坐标系。令所求场点P位于坐标轴Z轴上,且坐标为(0,0,a)。根据球体的对称性,此处只讨论上半球体,即a>0。将均匀带电球体分解成无数个均匀带电圆盘体积微元。大学物理教材中均匀带电圆盘轴线外一点处场强公式[3]为
(2)
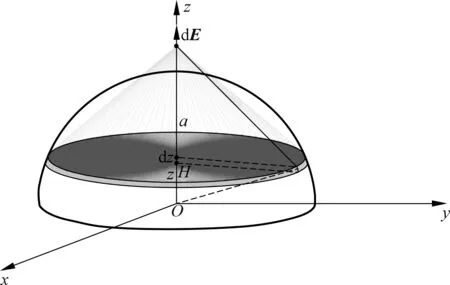
图1 均匀带电半球示意图
式中,σ为圆盘电荷面密度;R为圆盘半径;x表示圆盘轴线上的场点位置。利用公式(2)可以求出均匀带电球体分解出的每一个均匀带电圆盘体积微元在P点产生的电场强度dE。
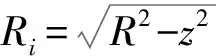
(3)
经计算,得到结果
(4)
显见,当a>R时,即场点位于球体外,结果与利用高斯定理计算结果相同。但当0≤a 既然推导过程没有错误,那错误应该出现在所用的公式上。重新检查均匀带电圆盘轴线上一点场强公式(2),发现如果将其理解为计算得到场强的矢量解,则场强不满足对称性,即不满足E(r)=-E(-r)。原来,公式(2)中的x仅表示坐标原点到P点的距离,故得到的场强E始终为正,只表示场强大小。笔者认为式(2)中的x为矢量坐标,计算得到的E值的正负可以确定场强方向,这才导致错误结果。但课堂中,老师强调电场强度是一个矢量,能否利用公式计算出的场强就是矢量呢?笔者试图自己推导出均匀带电圆盘轴线上一点场强矢量计算结果。 图2 均匀带电圆盘示意图 如图2所示,设圆盘半径R,电荷面密度为σ,令圆盘中心到轴线一点P的距离用一带有符号的标量r0表示,r0的符号选取原则为,设定圆盘一侧的场点与圆盘中心的距离为正,则另一侧为负。根据均匀带电圆环轴线上场强公式可得某一圆环微元在P点产生的场强为 (5) 图3 3种情形(a) 体积微元圆盘位于场点下侧; (b) 场点位于圆盘体积微元中心; (c) 体积微元圆盘位于场点上侧 式中,r为选取的圆环微元的半径。考虑到dq=σ2πrdr,对整个圆盘积分,可得 (6) 代入上下限,可求出均匀带电圆盘轴线上一点场强为 (7) 经过整理,利用符号函数[7],得到均匀带电圆盘轴线上一点的电场强度计算式 (8) 无论圆盘带电量是正还是负,其两侧的电场强度方向一定相反。则求解场点与圆盘中心的距离为正的一侧的电场强度时,上式中sgn(r0)=1,反之,sgn(r0)=-1。如此,根据式(8)计算均匀带电圆盘轴线上一点电场场强,可以满足E(r0)=-E(-r0),即圆盘两侧距圆盘中心相同距离的两个场点,其电场强度大小相等,方向相反。同时,由于符号函数定义了sgn(0)=0,所以利用式(8)求解圆盘中心的电场强度为零,而利用式(2)计算时,中心场强不为零,这也说明了式(2)的局限性。与式(2)相比,式(8)中将圆盘中心到场点的距离用符号函数来代替,这样就可以清楚地表示出当场点位于圆盘不同侧面时,场点的电场强度方向与圆盘之间的相对关系。笔者查阅了许多大学物理教材,虽然有部分教材对此有说明[8,9],但绝大多数教材中均匀圆盘轴线上的电场强度计算公式仍采用式(2)计算,并且对公式(2)中的x定义不明确,有的只在图中标出x,很容易使读者误解距离x为P点的矢量坐标,而利用公式(2)也只求解出场强大小,其方向还需另行说明[8,9]。也有其他的方法来计算均匀圆盘轴线上的电场强度[10],但式(8)给出的结果,更为简单,清晰。 既然得到了更为准确的均匀圆盘轴线上的电场强度计算式,利用其重新求解均匀带电球体内一点电场强度,验证一下结果是否正确。 如图3所示,仍取图1所示坐标系,考虑P位于球体内且在z轴正半轴的情况。对于组成球体的任意均匀带电圆盘微元会出现3种情况:带电圆盘微元在P上侧,即z>a;带电圆盘微元中心与P重合,即z=a;带电圆盘微元在P下侧,即z 如前所述,将式(8)中相关物理量变换,统一积分变量,可以得到均匀带电球体的场强求解式。因为式(8)中有符号函数,而根据前文分析,可以用积分变量z来判断所求场点位于当前圆盘微元的上侧还是下侧,即用z来确定符号函数的取值。 利用圆盘微元求解均匀带电球体场强,积分变量的范围为-R~R。如图3所示,将圆盘微元分成在场点上侧和下侧后,利用式(8)可将式(3)变换为 (9) 不同位置的圆盘位于场点的不同侧,当z的积分范围为-R~a时,圆盘微元位于所求场点P的下侧,r0符号与a-z同为正,如图3(a)所示;当z的积分范围为a~R时,圆盘微元位于所求场点P的上侧,r0符号与a-z同为负,如图3(c)所示。 先计算出带电微元在场点产生的电场强度,然后对带电体求场强的矢量和。利用这种场强叠加法求解电荷均匀对称分布的带电体的电场是大学物理教学中的重要内容。根据现有大多数教材给出的均匀带电圆盘轴线场强计算式(2),由于说明不清,很容易会错误的理解为场强的矢量结果,因此,得到的均匀带电球体场强也是错误的。本文引入符号函数,重新推导了均匀带电圆盘轴线场强计算式。该公式不仅可以计算出场强的大小,也清楚的表示出场强相对于圆盘的方向。根据场强叠加法利用该公式求解均匀带电球体的电场分布,得到了正确的结果。若大学物理教材中对均匀带电圆盘轴线上一点场强公式进行补充说明,或采用式(8)代替式(2),虽然改动微小,但表达清晰准确,体现了学习物理知识的严谨性。 [1] 程守珠,江之永. 普通物理学上册[M]. 6版. 北京:高等教育出版社,2006. [2] 张三慧. 大学物理学第三册[M]. 2版. 北京:清华大学出版社,1999. [3] 詹煜,张成义. 大学物理教程(下册)[M]. 2版. 北京:科学出版社,2011. [4] 周海英. 均匀带电薄圆盘的电场[J]. 大学物理,2005,24(11): 31-34. Zhou Haiying. The electric field of a uniformly charged thin disk[J]. College Physics, 2005, 24(11): 31-34. (in Chinese) [5] 吴崇试. 均匀带电圆盘电场的静电势问题[J]. 大学物理,2000,19(11): 1-4. Wu Chongshi. Electrostatic potential of electric field on a uniformly charged disk[J]. College Physics, 2000, 19(11): 1-4. (in Chinese) [6] 吴崇试,张之翔. 轴对称荷电圆盘的静电势[J]. 大学物理,2000,19(12): 5-8. Wu Chongshi, Zhang Zhixiang. Electrostatic potential of an axially symmetric charged disk[J]. College Physics, 2000, 19(12): 5-8. (in Chinese) [7] 李刚,王顺凤,朱凤琴,等. 高等数学(上)[M]. 北京:高等教育出版社,2010. [8] 惠和兴,郑锡琏. 普通物理学(2)[M]. 北京:北京理工大学出版社,1997. [9] 卢德馨. 大学物理学[M]. 北京:高等教育出版社,1998. [10] 李瑾. 均匀带电圆盘电场的研究[J]. 陕西学前师范学院学报,2014,30(5): 123-125. Li Jin. Study of electric field of uniform charged disk[J]. Journal of Shaanxi Preschool Teachers College, 2014, 30(5): 123-125. (in Chinese)2 引入符号函数的均匀带电圆盘轴线上场点的电场强度
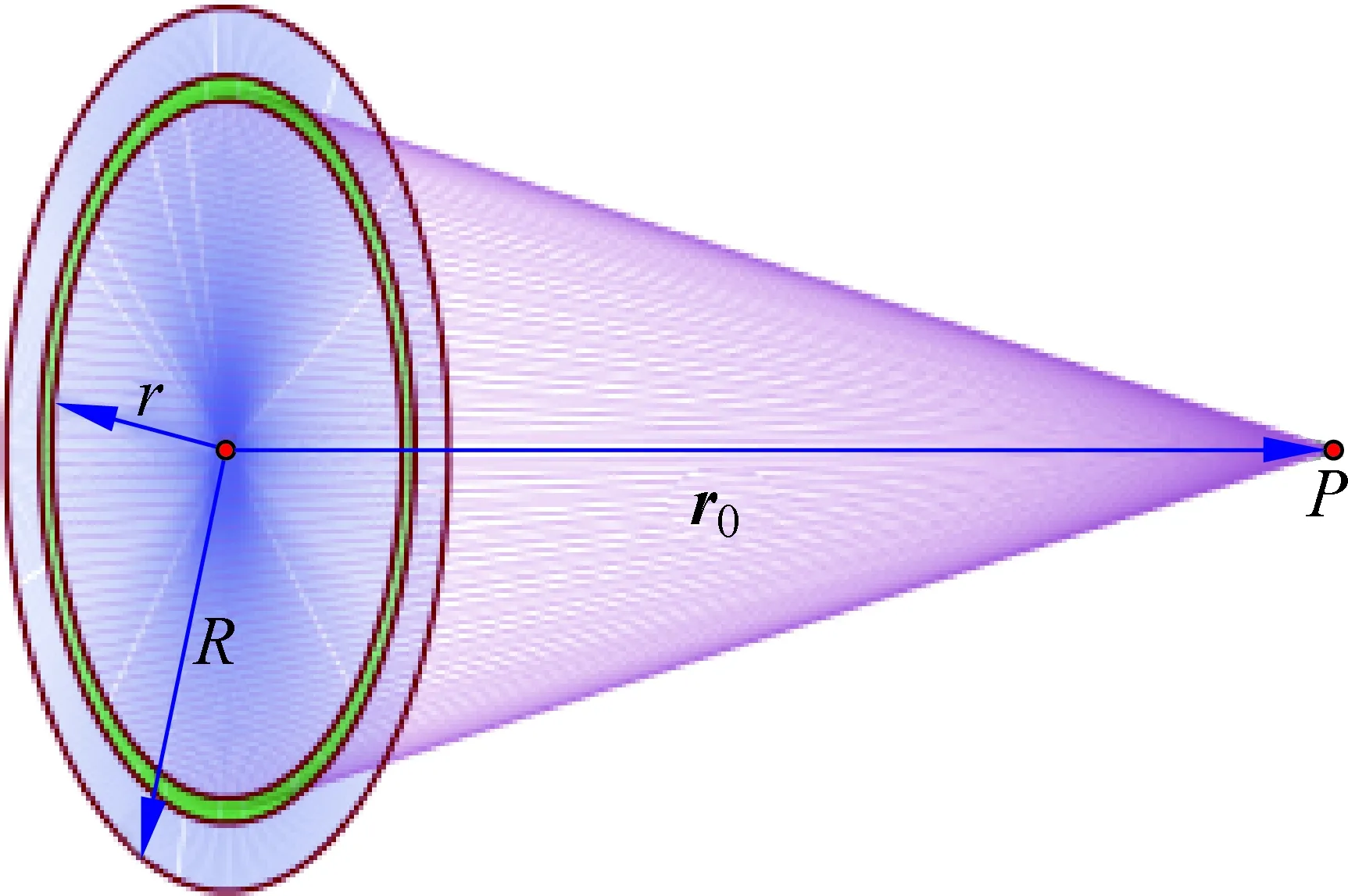

3 叠加法求解均匀带电球体场强
4 结语
