随机振动螺栓松动数值仿真分析
2018-01-19朱光宇郑保仲
朱光宇,郑保仲
(福州大学 机械工程及自动化学院,福建 福州 350002)
1 引言
在机械设计中,由于很多零件都处于随机振动载荷工况下,伴随着随机振动失效预测及有效控制是结构设计中的关键,而随机振动外载荷不像其他载荷可以用确定的函数表达,但人们对随机振动的研究步伐从未停歇。人们把统计学、通讯噪声及湍流理论移植到机械结构随机振动中去研究。
FPK方程法[1],随机平均法[2],随机等效线性法,柔性结构随机等效线性法均是研究单自由度非线性随机振动常用的方法。其中由林家浩提出的虚拟激励法[3]将平稳的随机振动转变为简谐振动,大大提升运算速度及效率,而Pradiwarter和Harnpornchai采用MonteCarlo法[4]对结构进行非线性随机振动分析,但该方法求解精度是以牺牲计算时间为代价,故对大规模多自由度系统该方法不能适用,文献[5]最早提出等效线性化方法在实际工程中应用较为普遍。随着计算机硬件资源高速发展以及模拟仿真软件的不断升级换代,运用有限元法数值模拟非线性系统在时域中的随机振动。其原理是通过给定的随机振动加速度功率谱密度采用文献[6]转化为随机振动的时域信号供大型显示有限元软件计算。螺栓联接是一种结构设计中普遍存在的紧固方式,而螺栓联接在随机振动作用下轴向力跳跃关系着联接的失效与否,故对随机振动环境下的螺栓联接可靠性提出更高的要求。实际以某款电动车车载充电机为主体,充电机用四个螺栓与车架相连,载荷的来源主要是通过车架传来的路面不平度激励,考查连接充电机螺栓预紧力变化情况及螺栓等级选择。运用SineOnRandom法生成振动信号时域样本,采用显示非线性求解施加预紧力螺栓轴向力响应情况。
2 随机振动信号转化原理
统计信号有两种方法:一种是将信号采集成时域函数,另一种是将采集的信号通过傅里叶转换成频率函数。时间函数是真实世界中唯一存在的,同时产品的安全性最终也是在时域中检测的。频域不是真实存在的,它是一种数学构造,遵循特定的数学范畴,同时正弦波的频域,且时域中的任何波形都可以用正弦波叠加,这是正弦波一个十分重要的性质。根据信号等效原理,转化前后信号的统计学特性是一致的。依据随机振动数学函数关系,功率谱密度表达式[7-8]:
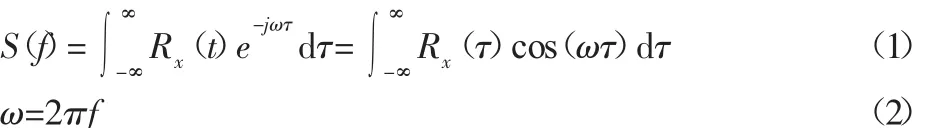
式中:f—振动频率;R(τ)是互相关函数,对于一个正弦位移信号:
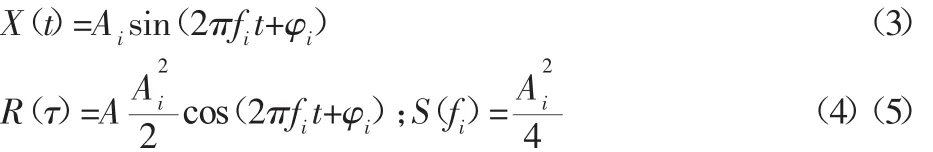
可见正弦波的功率谱密度是一冲击常数,其值与φ无关,在频域中每个频率点都有本身的幅值与相位。按谐波的频率、幅值、相位等信息可以求得谐波所对应时域的波形,最后将各谐波的时域叠加起来,即转化成时域中的信号波。将所要转换的功率谱密度函数所对应的频率区域(fstart,fend)划分为n个区间,用第i个区间的中点频率fmid,i的功率谱密度来替代该区间的功率谱密度大小,所以第i个区间上的功率谱密度:

式中:Gq(,)—位移密度谱;Δfi—频率间隔
因此,当随机振动过程采用正弦信号叠加法模拟随机过程的表达式为:
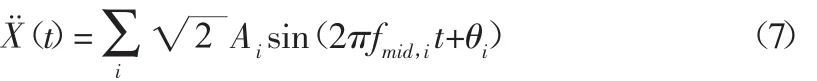
SineOnRandom法合成随机振动时域信号适用于模拟具有任意形状的谱密度的平稳随机过程,而且所得到结果的样本是连续的。值得注意的是,等效信号的时间样本大小应根据标准正态分布均值方差均方值等一致的前提下尽量缩短计算时间。
3 显式计算中心差分法
用世界上著名的通用显式动力分析有限元软件LSDYNA[9-10],该求解程序特别适合求解冲击碰撞仿真,特别是在高应变率数值计算中优势明显。LSDYNA显示动力分析采用中心差分法,第n个时间步结束时刻的加速度由速度的一阶中心差分给出,速度由位移的一阶中心差分给出向量通过下式表达:
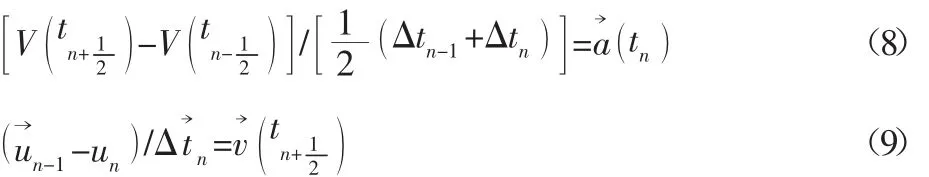
显式算法的特点是:(1)不形成总体刚度矩阵,弹性项放在内力中,避免了刚度矩阵的求逆,大大减小了求解程序对计算资源的占用,特别是对于非线性分析非常有益,避免在分析步中由于每个增量步都会带来刚度矩阵的变化重新计算带来的代价。(2)质量阵为对角时,利用中心差分法计算运动方程时不需要进行质量矩阵的求逆运算,仅仅利用矩阵的乘法得到等效载荷,计算效率很高。(3)中心差分法是条件稳定算法,保持稳定状态需要相对较小的时间步长,因此在计算模型设定时需减小初始时间增量步保证计算稳定。
4 数值模拟随机信号获取
数值模拟采用新国标GB/T 31467.3-2015,规定的振动功率谱密度要求,如图1和表1所示。由于表的频谱数据是根据实际路谱采集信号经过信号处理后再由FFT变化得到的原始功率谱密度,但该功率谱密度是频域范围内的,不能用于时域的非线性系统计算,因此在信号处理软件中采用SineOnRandom方法产生随机振动时域信号波。信号的失真度由采样频率,计算时间控制,前提是保证产生的时域信号加速度均方值与原始数据相差不大,通过不同组合得到的样本,如表2所示。通过表数据规律分析可知,运用SineOnRandom方法获取的时间样本由于采样频率及样本大小不同会产生不一样的模拟时域信号,且信号的加速度峰值存在着这样一条规律:样本越小,则采样频率越高才不会使信号失真过多,反之则采样频率相对下降才会使加速度峰值靠近原始值。考虑到计算效率及样本失真度,采用时间样本为1s,采样频率为4500Hz进行样本抽取。但遵循的原则是样本信号经过傅立叶变换与原始功率谱密度进行比对,失真度不能过高,在保证要求的前提下尽量的缩短计算时间,否则会给后续的有限元计算带来沉重的负担。
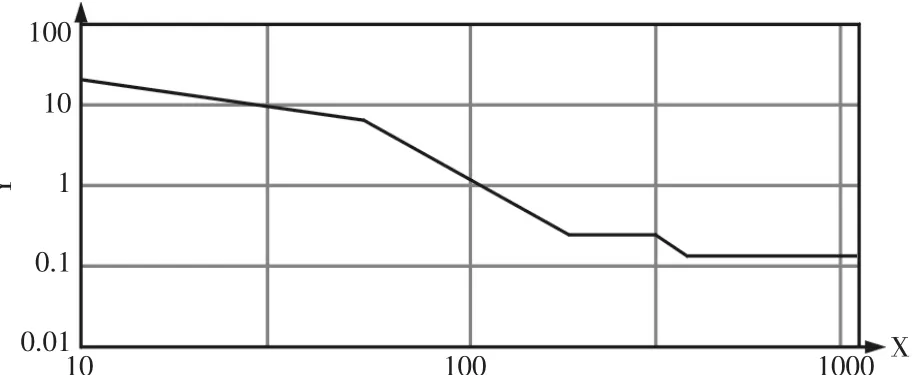
图1 加速度PSD和频率对应关系Fig.1 Acceleration PSD and Frequency Correspondence

表1 PSD值和频率Tab.1 PSD Value and Frequency
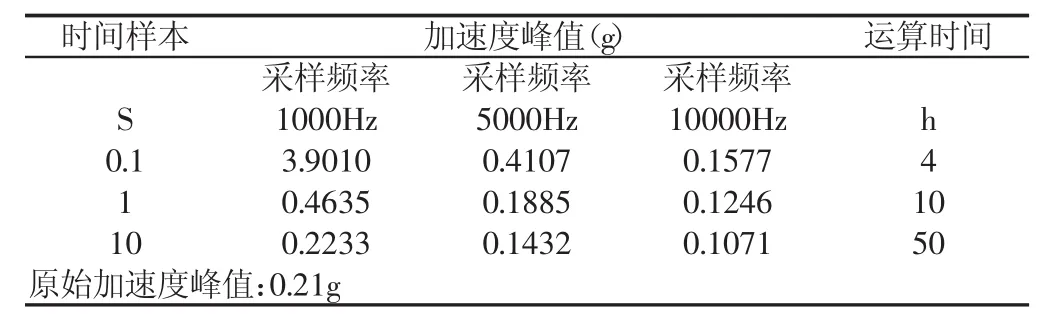
表2 时间和加速度峰值Tab.2 Time and Peak of Acceleration

图2 原始与模拟功率谱密度比对Fig.2 Comparison of Original and Simulation Power Spectral Density
如图2所示,模拟功率谱与原始功率谱在随机振动所关注的低频段误差在可接受范围内,这样保证了信号转换前后的一致性,即失真度达到要求的情况下可以等效的认为转换后的时域信号可以替代随机振动的功率谱密度信号。在随后的非线性有限元计算中作为载荷输入条件,通过计算时间轴函数来表达各个要求物理量的时域响应特性。
5 随机振动数值仿真实际案例应用
仿真建模思路参照实际装车中充电机的装配关系,截取与之相关的几何零部件离散成有限元网格集合,由于仿真中不考虑焊接关系对结构刚度影响,故对焊接关系采用刚性连接替代建立整个系统的仿真模型,其中所有参与振动的部件全部加入接触考虑接触非线性及几何非线性和材料非线性,并且对紧固充电机的四颗螺栓采用beam单元模拟实际的螺栓连接,beam单元与联接的两个零部件采用刚性耦合,通过对beam单元施加预紧力模拟实际装车条件下的预拧紧力矩,通过beam单元在振动时域信号下的轴向力响应输出来判断螺栓是否会发生松动模型,如图3所示。
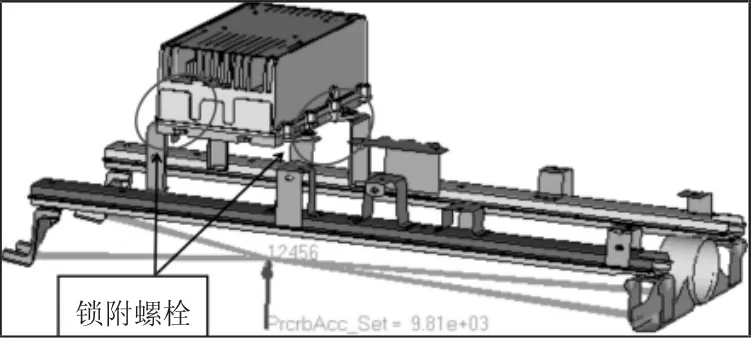
图3 数值计算模型Fig.3 Numerical Compute Model
模拟仿真主要考查车载充电机紧固螺栓振动强度,故对非关注区域的有限元离散不做详细要求,由于充电机内部电子元件复杂导致建模费时费力又不是计算关注点,故对充电机内部进行简化,采用配重的方式保证充电机质量及惯量一致即可。另外整个模型网格大小为5mm,激励源为与车架连接处,约束激励处的5个自由度,放开Z方向的平动自由度。通过不同组合仿真计算结果,如表3所示。
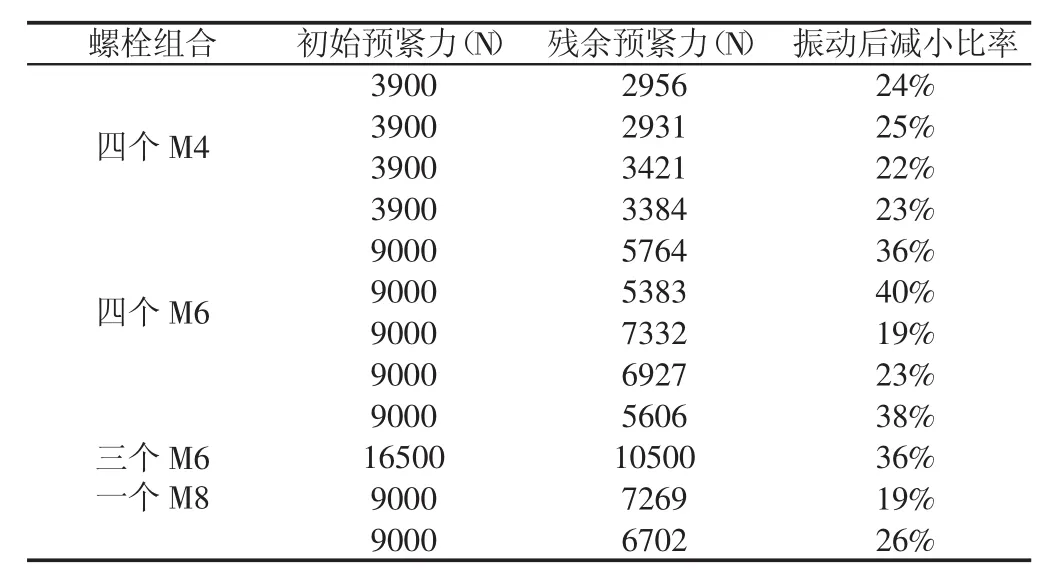
表3 不同仿真工况结果Tab.3 Different Simulation Condition Result
由表3可以得出,不同的螺栓组合由于不同的初始预紧力及结构不对称导致不同的振动后力量减小比率。且根据数据规律发现,螺栓等级强度越高,由于初始预紧力很大导致力量掉落比较厉害。通过仿真发现高强度螺栓在振动一开始预紧力就掉落厉害,且由于预紧力增大结构不对称导致螺栓上力量分布差距更加明显,故振动后力量减小厉害。
6 实验验证
该实验由振动台、夹具、试件等组成。分别采用M4,M6,M8不同强度等级的螺栓依规定的初始拧紧力矩把充电机锁附在振动台面上,如图4所示。实验参照GB/T2423.56执行随机振动,进行8h的振动后测试充电机上螺栓残余预紧力大小并与仿真比对结果,如表4所示。

图4 振动试验Fig.4 Vibration Test
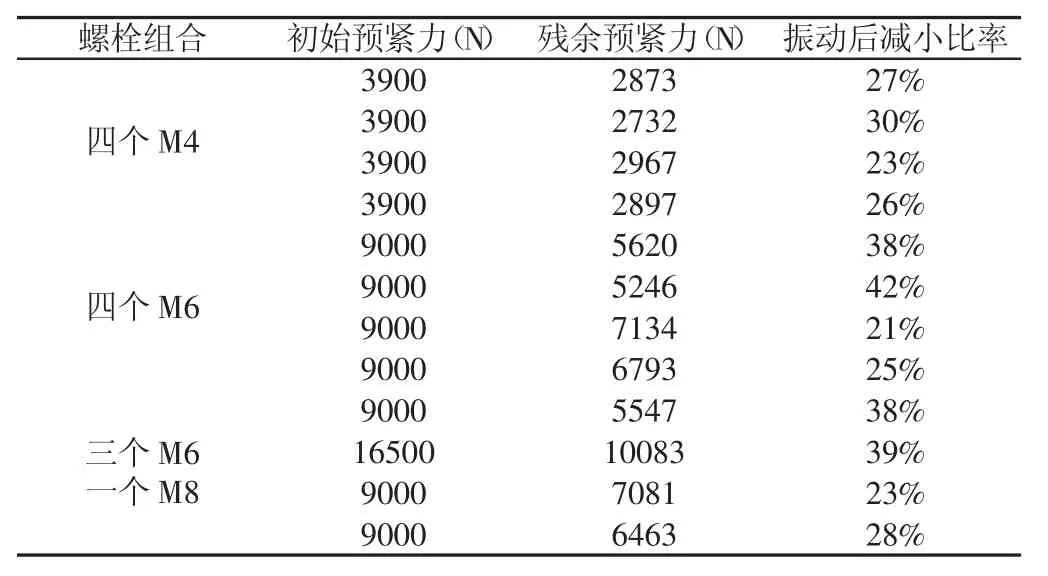
表4 振动前后对照表Tab.4 Collation of Vibration Test
由表4可以得知,试验过后螺栓预紧力减小相对于仿真计算更厉害,但在误差控制在合理范围内说明仿真计算结果还是可以接受。而且通过实验也可以说明实际振动过程中螺栓预紧力跳动更大,后续在数值仿真中须对时间样本容量及采样频率作进一步的研究以取得更为精确的样本信号以提升仿真计算精度。
7 结论
(1)采用SineOnRandom法把随机振动信号由频域转换成时域,从而使得随机振动在显示非线性计算中实现复杂的接触行为及性能参数响应。(2)通过SineOnRandom法获取时间样本容量须根据计算机性能谨慎选择,但基本原则是时间样本容量在统计学上的均值,方差及均方值与原始信号一致的前提下适当获取。(3)通过仿真很好地验证了实际设计中不同等级强度的螺栓在随机振动过程中的强度原则。
[1]Caughey T-K,Ma F.The exact steady-state solution of a class non-linear stochastic[J].International Journal of non-linea Mechanics,1982,17(3):137-142.
[2]Zhu Wei-qiu.Recent developments and applications of the stochastic averaging method in randomvibration[J].Applied Mechanics Reviews,1996,49(10):72-80.
[3]林家浩,张亚辉.随机振动的虚拟激励法[M].北京:科学出版社,2004.(Lin Jia-hao,Zhang Ya-hui.Pseudo-excitation method in random vibration[M].Beijing:Science Press,2004.)
[4]Harnpornchain Stochsstic analysis of dynamical systems by phase-spacecontrolled Monte Carlo simulation[J].Computer Methods in Applied Mechanics and Engineering,1999,168(1-4):273-283.
[5]Caughey T-K.Equivalent linearization techniques[J].Journal of coustical Society of America,1963,35(11):1706-1711.
[6]Ansys ncode designlife Help
[7]杨文,郭连水.螺纹连接非线性随机振动仿真分析[J].机械工程学报,2000,49(560):9-13.(Yang Wen,Guo Lian-shui.Simulation analysis of nonlinear random vibration of thread connection[J]Journal of Mechanical Engineering,2000,49(560):9-13.)
[8]张言,曾国英,赵登峰.振动环境下螺纹连接松动的实验研究[J].中国重型装备,2010,36(4):23-25.(Zhang Yan,Zeng Guo-ying Zhao Deng-feng.Experimental research on threadconnectionloosenessinvibrationenvironment[J].ChinaHeavyEquipment,2010,36(4):23-25.)
[9]Ls-dyna keyword user’s manual volume
[10]刘文光,陈国平,贺红林,吴晖.结构振动疲劳研究综述[J].工程设计学报,2012,36(4):1-6.(Liu Wen-guang,Chen Guo-ping,He Hong-lin,Wu Hui.Review of studying on vibration fatigue[D].Chinese Journal of Engineering Design,2012,36(4):1-6.)
