磨床砂轮动平衡测控系统控制新策略
2018-01-19张琳娜薛靖雯
薛 兵,张琳娜,郑 鹏,薛靖雯
(郑州大学 机械工程学院,河南 郑州 450001)
1 引言
精密磨削加工过程中,磨床砂轮的振动不平衡会对磨削加工造成不利影响。不仅会影响被加工工件的表面质量,导致废品率升高,还会影响砂轮及磨床的使用寿命。目前,砂轮平衡采取的主要措施是安装前的静平衡,主要依靠工人的技术经验,操作繁琐,精度差。在磨加工过程中,砂轮的磨损、冷却液的吸附还会引起砂轮的振动不平衡。随着当前精密技术的发展和工业自动化水平的提高,日益要求解决砂轮的动平衡问题,砂轮动平衡仪应运而生[1]。它能够在磨加工过程中在线监测砂轮的振动不平衡量,并将测量数据反映给动平衡仪,从而控制动平衡头,实现磨床砂轮的动平衡补偿。
DPH-1型测控仪是东京精密与中原精密早起合作生产的产品。其以振动幅值、相位为参数,采用逐步寻优的平衡算法来调整加工过程中出现的不平衡量,虽然精度较高但耗时长,效率低下,亟需寻找一种新的控制算法对产品进行升级换代。
变结构控制是自动控制系统一种普遍的设计方法。它可以在动态过程中,根据系统的当前状态有目的的不断变化,迫使系统按照预定“滑动模态”的状态轨迹运动[2]。在分析磨床砂轮动平衡测控仪的结构特点和工作原理的基础上,进一步研究平衡头的控制策略。提出以变结构控制理论为基础,采用基于组合趋近律的滑模变结构控制方法,来实现磨床砂轮的在线动平衡,通过实验验证并与现有平衡头控制策略作分析比较,验证了滑模变结构控制算法能够在较短时间内补偿磨床砂轮的振动不平衡量,精度达到(0~0.2)μm,有效提高了动平衡效率。因此,此项技术具有较高的使用前景和经济价值。
2 动平衡测控系统的原理及结构
以DPH-1磨床砂轮动平衡测控仪为研究基础,该系统采用模块化设计,主要由不平衡量采集模块、控制器模块、平衡头控制模块、LCD显示模块和键盘控制模块组成。系统的整体结构,如图1所示。系统通过加速度传感器采集砂轮的不平衡振动信号,通过霍尔传感器获得砂轮的转速。测控系统采用脉冲测振法获得振动不平衡量的幅值大小和相位,即采集振动不平衡信号的同时以相同频率触发转速信号采集,将转速信号作为键相脉冲基准信号,然后将振动信号与键相脉冲基准信号二者作比较得到相位差值,从而得出振动不平衡量的幅值和相位。当砂轮的振动不平衡量被检测后,动平衡测控系统根据测量值控制平衡头内部电机的转动,调节偏心齿圈的位置,使砂轮达到平衡状态。DPH-1磨床砂轮动平衡测控仪采用FL1300型号平衡头,其结构主要由驱动单元、传动系统和偏心齿圈组成。驱动单元采用20ZYW6型直流永磁电机,调速性能较好且体积小。传动系统采用蜗轮蜗杆和精密齿轮系,实现运动的传递和平衡后偏心齿圈锁定。电机的运动经过一级蜗轮蜗杆传动后将旋转运动传给齿轮轴,经过二级蜗轮蜗杆传动传给内啮合齿轮,最后经过内啮合齿轮传动传给偏心齿圈,即平衡块。
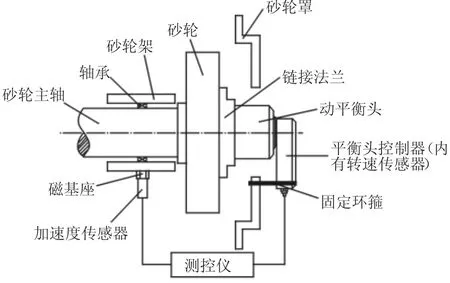
图1 磨床砂轮动平衡测控系统整体结构图Fig.1 Grinding Wheel Dynamic Balance Measurement and Control System as a Whole Structure
3 动平衡测控系统的控制策略
3.1 平衡原理及建模
砂轮出现振动不平衡时,20ZYW6型直流永磁电机经蜗轮蜗杆和精密齿轮系减速后带动偏心齿圈的移动,测控系统通过控制两个直流永磁电机的控制电压u1、u2的通电时间,就可以得到偏心齿圈的相对转角。首先保持偏心齿圈的夹角不变使电机同向转动,当偏心齿圈的合成不平衡量变化到与振动不平衡量反向成180°时,达到相位平衡,然后调节两偏心齿圈之间的夹角,当系统指示到最小值时,达到幅值平衡。
测控系统对平衡头的控制就是对直流永磁电机转角和转向的控制,即对电机控制电压的调节,由电机电势平衡方程和转矩平衡方程,建立其数学模型。电机原理图,如图2所示。
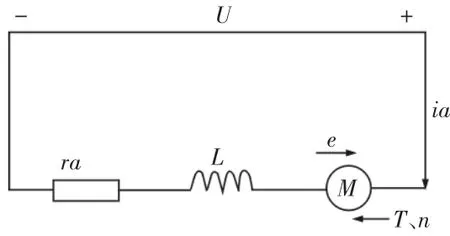
图2 电机原理图Fig.2 Electrical Principle Diagram
电势平衡方程:
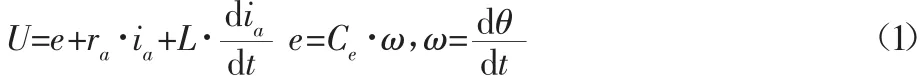
转矩平衡方程:

式中:Ce,Ct—感应电动势系数和转矩系数;T,TL—总电磁转矩和负载转矩;J—电机转动惯量。
3.2 基于趋近律的滑模变结构控制
探讨公路桥梁建设中存在的问题及解决对策…………………………………………… 莫轻文,陈景丽(1-121)
在滑模控制中,对于线性系统有:x˙=Ax+bu
其中,x满足x˙i=xi+1,i=1,…,n-1
结合电机电势平衡方程和转矩平衡方程式,根据式(1)、式(2),故令 x1=θ,x2=ω,x3=ia可得:
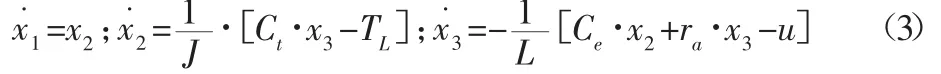
作状态变换,令 y1=x1,y2=y˙1,y3=y˙2可得:
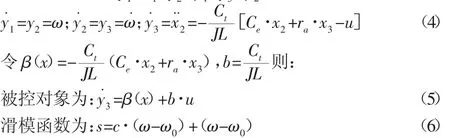
式中:c>0,满足Hurwitz条件,ω-ω0—跟踪误差。
滑模变结构虽与参数摄动和外部扰动无关,但由于时滞特性、系统惯性及系统本身造成的影响,系统到达滑模切换面后,总是在滑模面两侧来回穿越产生抖振现象[3]。采用组合趋近律的方法来改善系统趋近滑动模态后的动态品质,在滑模运动前期,采用基于指数趋近律的控制律,滑模运动的后期和稳定段,采用基于变速趋近律的控制律。
滑模运动前期,指数趋近律为:s˙=-εsgns-ks ε>0,k>0 (7)
结合式(4)~式(7)可得滑膜运动前期的控制律为:
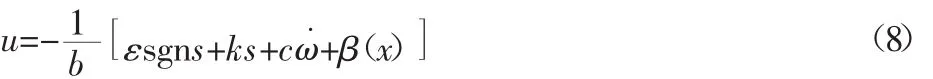
滑模运动后期和稳定状态,变速趋近律为:

由式(5)~式(7)、式(10)可得滑模运动后期和稳定段的控制律为:
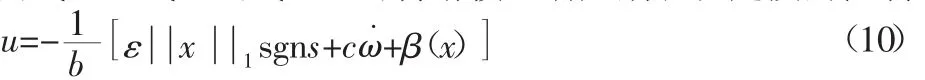
选定一个正的实数t0作为控制律的转换点,综合两种趋近律的优点,使系统性能达到最优,转换点的选择依据实际情况确定。取t0=0.6。由式(8)、式(10)得系统的整个滑模变结构控制律为:
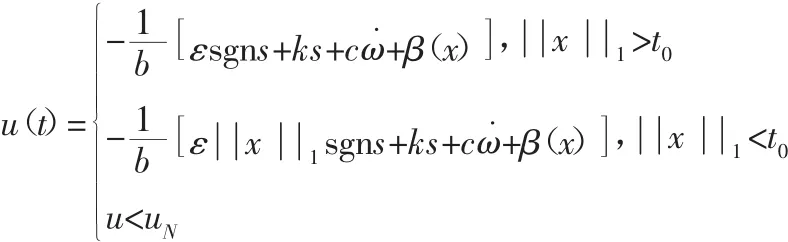
式中:uN—电机额定电压。
通过单片机控制两个20ZYW6型直流永磁电机的通电时间调节电机转动,电机经蜗轮蜗杆和精密齿轮系减速后,能够准确获得偏心齿圈的相对转角,实现偏心齿圈的精确移动,完成砂轮的在线动平衡补偿。
3.3 平衡程序流程
程序编写基于Keil MDK平台,C语言为其汇编语言。振动不平衡量信号被采集后,经A/D转换、数字滤波整合成单片机能够处理的数字信号。振动不平衡量的处理采用定时中断方式。当振动不平衡量超过设定值时,进行手动动平衡操作;振动不平衡量未超设定值,测控系统进行自动平衡,获得振动不平衡量的幅值和相位后,先判断偏心齿圈当前位置,计算偏心齿圈需要移动到的位置,单片机发送移动指令,控制电机转动,调节偏心齿圈位置,使系统达到动平衡状态。中断平衡程序流程图,如图3所示。
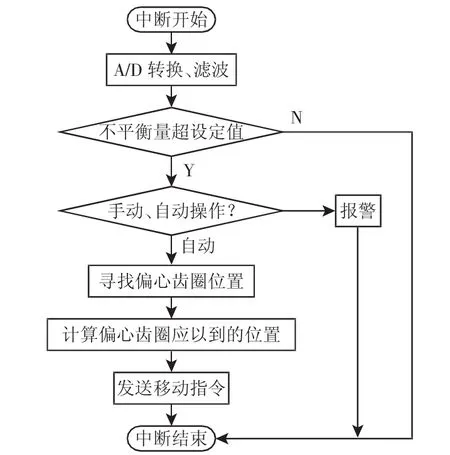
图3 中断平衡程序流程图Fig.3 Interrupt Balance Program Flow Chart
4 动平衡过程仿真和实验测试分析
利用MATLAB中的罗盘向量图进行控制新策略的动平衡过程的仿真。在MATLAB中产生一个砂轮的振动不平衡量,其幅值为(1~6)的一个随机数,相位为(0~2π)的一个随机数。再生成两个偏心齿圈,其幅值假定为4,相位为(0~2π)的一个随机数。两个幅值为4的点画线向量为偏心齿圈不平衡量,幅值约为4.5的实线向量为砂轮的振动不平衡量,如图所示。由图4可以看出此时平衡头对砂轮的振动不平衡量不但没有减小的趋势反而砂轮与平衡头的整体不平衡量增大。需要进行自动平衡,首先进行相位平衡,保持偏心齿圈的夹角不变使其同步转动,当偏心齿圈的合成不平衡量变化到与振动不平衡量反向成180°,为进一步减小砂轮振动不平衡量,应进行平衡块合量的幅值平衡,两个电机一个正转一个反转同步转动,仿真结果,如图4所示。
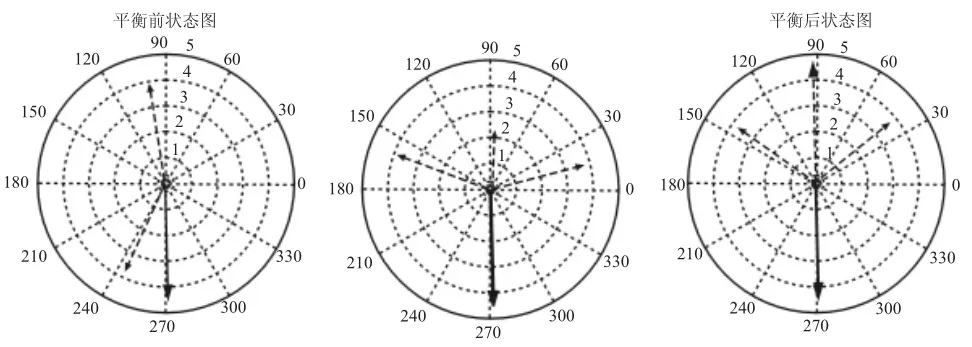
图4 相位平衡和幅值平衡向量图Fig.4 Phase Balance and Amplitude Vector Diagram
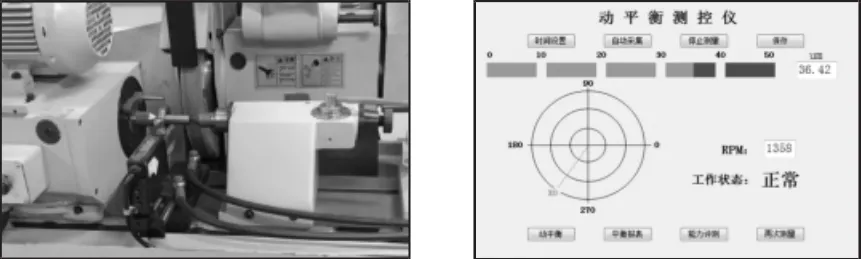
图5 磨削实验Fig.5 Grinding Experiment
为验证动平衡控制器的工作性能,在实验室的MGB1320E型高精度半自动外圆磨床上进行实验分析。磨削工件材料为45钢,磨削外圆直径为24mm,主轴转速设置在1400r/min,磨削方式为外圆切入磨。实验装置,如图5所示。对采用逐步寻优控制算法和滑模变结构控制算法的动平衡仪在同一磨床上对一批工件进行磨削试验。实验结果,如表1所示。

表1 不同控制算法磨削实验对比结果Tab.1 Grinding Experimental Comparison Results
由表1可知,对磨床砂轮动平衡头的控制电机采用滑模变节构控制能够有效提升动平衡精度,精度达到(0~0.2)μm,动平衡的时间有效缩短,平衡时间可以提升50%。工件的表面粗糙度作为衡量磨床磨削性能优劣的重要指标,故采用测量加工工件的表面粗糙度来验证控制器系统的稳定性,工件的表面粗糙度采用2206B型表面粗糙度测量仪测量,每个工件在圆周方向上以120°为间隔测量3次表面粗糙度,取平均值,测量结果,如表2所示。由表2的测量结果可以看出后工件的表面加工质量较为良好,表面粗糙度值控制在0.4以下。由此证明控制器系统的工作性能优异,稳定性好。同时实验结果也表明改进的磨床砂轮动平衡测控系统不但控制性能良好,而且系统运行速度快,性能可靠,实时性好。测量表面粗糙度,如图6所示。

图6 测量表面粗糙度Fig.6 Measuring Surface Roughness
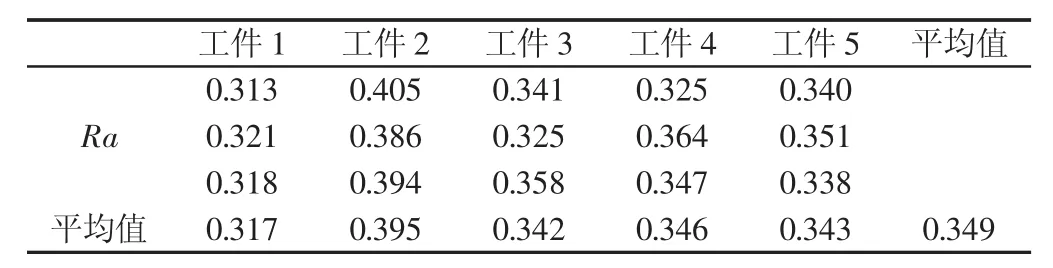
表2 工件粗糙度测量结果Tab.2 The Workpiece Roughness Measurement Results
5 结论
采用基于组合趋近律的滑膜变结构控制方法来控制平衡头内部两个直流电机的转动,对于砂轮的不平衡调整取得良好的效果,平衡时间比现有设备有明显的提高。由此证明采用该控制方法的测控仪能够有效提高生产效率。此外,经实验分析证明测控仪能够减少被加工工件废品率,满足工业自动化的要求,对精密加工技术的发展具有极为重要的支撑推动作用和广阔的产业应用价值。
[1]田力波,佟大鹏.基于DSP的砂轮动平衡测控系统[J].科技创新导报,2010(33):121.(Tian Li-bo,TongDa-Peng.Grinding wheel dynamic balance measurement and control system based on DSP[J].Science and Technology Innovation Herald,2010(33):121.)
[2]刘金琨.滑模变节构控制MATLAB仿真[M].北京:清华大学出版社,2012.(Liu Jin-kun.Defect Structure Sliding Mode Controller is MATLAB Simulation[M].Beijing:Tsinghua University Press,2012.)
[3]高为炳.变节构控制理论及设计方法[M].北京:科学出版社,1996.(Gao Wei-bing.Defect Structure Control Theory and Design Method[M].Beijing:Science Press,1996.)
[2]郑鹏,张琳娜,陶金伟.具有断续表面特征零件的磨削加工在线测量方法[J].机械设计与制造,2014(3):110-113.(Zheng Peng,Zhang Lin-na,Tao Jin-wei.An on-line grinding measuring method for workpiece with intermittent surface[J].Machinery Design&Manufacture,2014(3):110-113.)
[5]杨晓红.不平衡量信号的精密谱分析及其在砂轮动平衡测控仪中的应用[D].长春:中国科学院研究生院(长春光学精密机械与物理研究所),2006.(Yang Xiao-hong.Rough measure the precision of signal spectrumanalysis and its application in the grinding wheel dynamic balance measurement and controlinstrument[D].Changchu:Graduate School of Chinese Academy of Sciences(changchun institute of optical precision machinery and physical),2006.)
[6]秦源章,张琳娜,郑鹏.基于单片机的磨床砂轮动平衡测控系统的设计[J].制造技术与机床,2015(10):50-53.(Qin Yuan-zhang,Zhang Lin-na,Zheng Peng.Grinding wheel dynamic balance measurement and control system based on single chip design[J].Manufacturing Technology and Machine Tools,2015(10):50-53.)
[7]郗元.砂轮不平衡量检测相关技术研究[D].长春:长春工业大学,2013.(Xi Yuan.Grinding wheel unbalancetesting related technology research[D].Changchun:Changchun University of Technology,2013.)
[8]TSENG C Y,SHIH T W,LIN J T.Dynamic balancing scheme for motor armatures.Journal of Sound and Vibration,2007.
