近场强震动记录基线校正方法的振动台实验研究1

卢 滔 胡国瑞 何 福 郭 迅 霍敬妍



近场强震动记录基线校正方法的振动台实验研究1

卢 滔 胡国瑞 何 福 郭 迅 霍敬妍

（防灾科技学院，北京 101601）

为了获取近场永久位移，通常采用基线校正方法，对近场加速度记录进行基线校正并积分得到永久位移值，但这一结果主观性较强，其可靠性也往往缺乏验证。为了解决这一问题，本文提出了一种能产生包含永久位移振动过程的振动台实验方案，采用振动台加滑动机构的方法，模拟记录到永久位移台站测点的真实振动情况；在实验中分别采用加速度计、摄影测量方法分别直接得到加速度和位移时程，对加速度时程进行基线校正并积分得到位移时程，将其与直接获得的位移时程进行对比，以验证采用基线校正方法的有效性。实验结果表明，在实验室条件下采用现有的基线校正方法校正后，通过积分能得到可以接受的位移时程。

近场 强震动记录 基线校正 永久位移 振动台实验

引言

近场强震动记录往往包含永久位移信息，不进行基线校正直接积分往往会使速度和位移时程出现非常明显的漂移现象，这与实际的情况是相悖的，而常规的基线校正方法和高通滤波处理的结果很难满足该类型强震动记录的处理要求（Trifunac，1971；Iwan等，1985）。为了更好地处理该类记录，得到可信的近场位移时程和永久位移，研究人员开展了大量的工作，并在研究成果的基础上提出了专门针对近场强震动记录的基线校正方法，并用这些方法对一系列强震动观测记录进行了处理（Iwan等，1985；Boore，1999，2003；王国权等，2004；Wu等，2007；周宝峰，2012）。

虽然大量的校正方法已用于处理实际记录，但都存在以下共同特性：①这些方法都是从数学意义上出发，令最终处理得到的速度时程趋向于0，位移时程末尾段与坐标轴平行，最后值即为永久位移（王国权等，2004）；②在处理过程中校正参数的选择主观性较大，最终得到的永久位移值的参数敏感性较大，很难确定参数选择何值是最优的，到底哪个校正结果是合理的（黄蓓，2003；王国权等，2004；陈勇等，2007）；③缺乏能施加符合真实工况（包含可精确测量的永久位移值）的振动台试验去验证方法的合理性及针对如何有效地选择参数而开展的讨论（于海英等，2009；胡国瑞，2016）。

在现有研究成果基础上，本文提出一种能产生包含永久位移振动过程的振动台实验方案，并开展振动台实验，通过实验数据分析讨论现有常用校正方法的有效性。

1 基于机器视觉的动态位移测量方法

在本试验中，动态位移过程是验证基线校正效果的最终直接对比物理量，获得较为精确的动态位移时程极为重要。现有的较大量程（位移达到几十厘米及以上）的宏观动态位移量测方式主要分为2大类，即接触式测量和非接触式测量。对于实验室的常规测量，前者主要使用拉线式位移计，后者主要使用激光位移计。然而，随着机器视觉和数字图像解析技术的发展，基于机器视觉的动态位移测量技术现也成为一种经济、可行的非接触式测量方式。相比拉线式位移计测量和激光位移计测量而言，基于机器视觉的测量方法具有量程范围大（cm—m）、测试成本较低（无须购置较为昂贵的专用设备）、多点测量同步效果好等特点，因此本实验选用其作为测量方法开展动态位移测量，并开发了相应的软件并进行了动态位移测量精度分析。

1.1 基于机器视觉的动态位移测量方法的工作原理

由图1可知，基于机器视觉的动态位移测量方法的工作流程大致分5个步骤：①采用高速摄像机采集带有标识点物体运动的动态视频；②对视频进行分帧，提取每一帧对应的静态数字图像；③开展数字图像识别，确定标识点圆心在每一帧图像中的位置（x,i，y,i）；④根据识别确定的圆心坐标计算当前帧圆心相对开始时刻（即第一帧）圆心的相对运动距离，即（X,i，Y,i）＝（x,i，y,i）－（x,1，y,1）；⑤根据图像中像素与实际长度的换算关系＝/，计算在当前时刻（即第帧时刻）的实际位移值（X，Y）＝×（X,i，Y,i），每一时刻实际位移值确定后即可得到物体标识点位置的动态位移时程。

图1 基于机器视觉的动态位移测量方法工作流程

不难看出，在上述测试流程中，从每一帧静态数字图像中准确识别出圆形标识点是方法实现的最重要的一步。本试验基于MATLAB自带的图像处理工具，先对静态数字图像进行降噪与灰度处理、标识点对应颜色提取，并将图形从RGB空间转换到HSV空间，然后针对HSV空间图层分量调用MATLAB软件自带的边缘检测算法模块对标识点进行精确识别定位（胡国瑞，2016）。在图形识别过程中，采用彩色（如红色）标识点对图像开展颜色提取时，除保留数字图像中标识点对应的色彩外，其他部分全部灰度化，以便提高图像的反差和饱和度差异，起到改善标识点识别效果的作用；对HSV空间分量进行边缘识别效果比直接在RGB空间进行识别效率更高，在图像背景噪声较高的情况下效果尤为明显，如图2所示。

图2 标识点识别算法及优化算法实现效果图

1.2 测试方法的精度对比分析

依据上述算法和流程，编制开发了基于机器视觉的动态位移测试分析软件——“基于数字影像特征标识点识别的动态位移测量系统（Video2DynaDisp）”，并采用如图3所示的实验系统验证软件的可行性并开展测试方法的精度分析。

该验证试验系统由简易振动模型和多种位移测试系统组成。简易振动模型为1个2自由度的钢制框架模型，测试实验中将模型第二层顶板自由振动时的动态位移时程作为观测对象，验证试验中采用3种方式，即使用拉线位移计、百分表和基于机器视觉动态位移测量系统进行位移测试并开展对比分析，其中将拉线位移计测量值作为本试验方法精度比较的标准值，百分表测量值作为控制值，并安放了加速度计实时记录加速度。为了比对机器视觉识别效果，本验证试验中还专门比较了白底红色标识点和黑底红色标识点的测试效果，并采用25帧/s和50帧/s的帧率摄制数字视频，最终图像解析得到的位移时程的采样频率分别为25Hz和50Hz。

图3 验证试验系统组成示意图和模型测点局部实际布置图

验证试验中采用中国地震局工程力学研究所研制开发的拉线位移计，加速度计为Kinematrics公司生产的ES-T三分向力平衡式加速度计，摄像设备为PENTAX K3数字单反数码相机。图4和图5为验证试验中采用不同方式获得的典型动态位移时程曲线和局部放大结果，其中图4为摄像帧率为25帧/s识别的结果对比，图5为50帧/s识别的结果对比。表1给出了机器视觉的动态位移测量方法基于不同测试方案得到的位移时程峰值和拉线位移计测得值的比较，其中基于机器视觉测量方法的测量值中，括号中的百分数表示该方案测试值与对应拉线位移计测量值的相对误差。

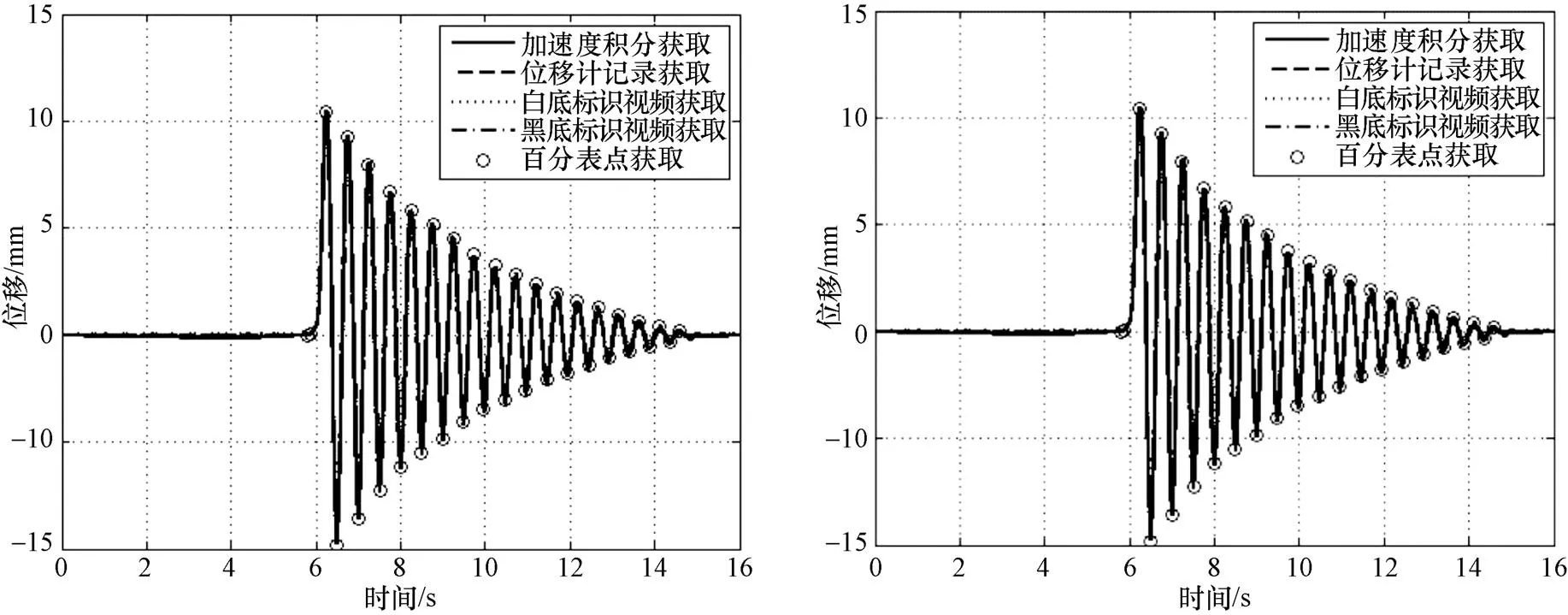
图4 摄像帧率为25帧/s时的实验数据处理结果及局部放大比较

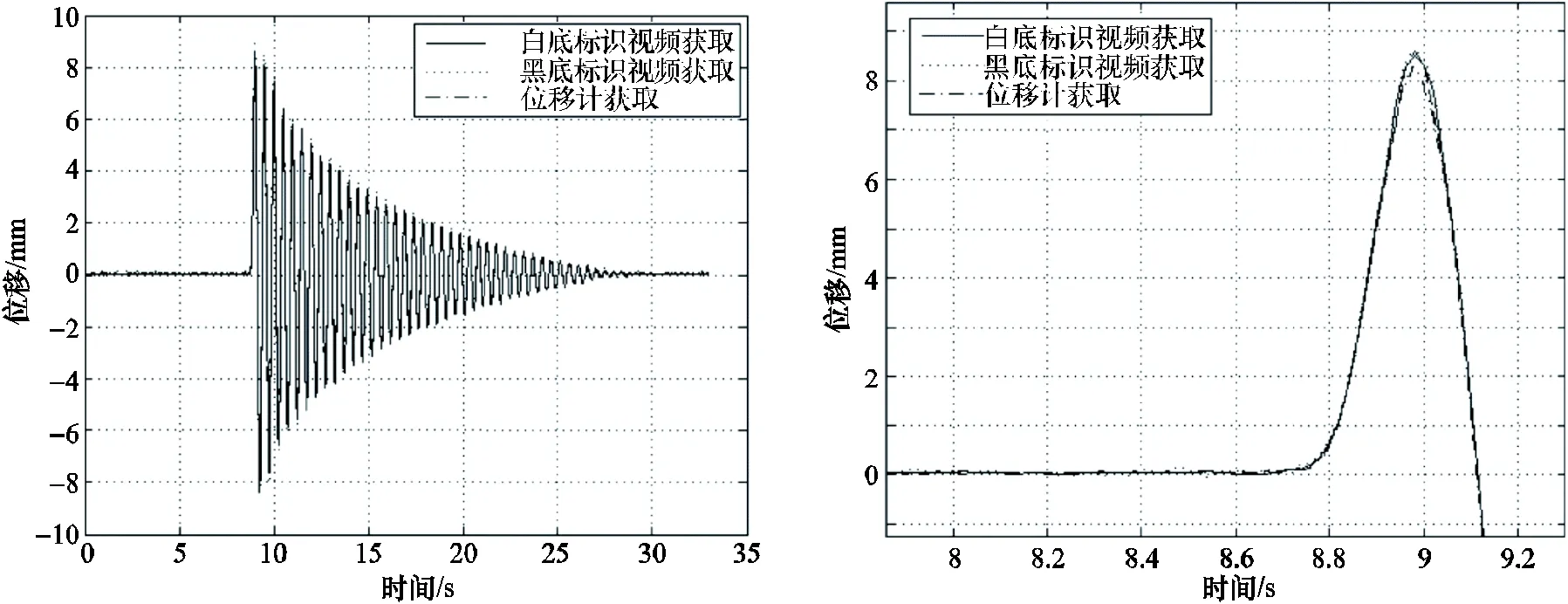
图5 摄像帧率为50帧/s时的实验数据处理结果及局部放大比较

表1 不同测量方法得到动态位移峰值

续表

通过比较验证试验的动态位移曲线和动态峰值后不难看出，在本实验中采用基于机器视觉的动态位移测量方法是可行的，相对拉线位移计测量值而言，其相对差值在5%以内，而且从表1中可以看出，摄像帧率越高相对误差值越小，尤其是采用白底红点标识方案时更为显著。同时，从图中的加速度积分位移时程曲线也可以看出，不存在永久位移的情况下，加速度积分得到的位移时程与实际位移时程也基本吻合。根据最终实验要求，在近场强震动记录基线校正方法振动台试验中，实验测试选用了50帧/s摄像，采用白底红色标识点及红色提取预处理方案开展相应研究。

2 近场强震动记录基线校正方法的振动台实验

2.1 实验基本思路

本实验基本思路是通过构建实验系统产生包含永久位移的振动过程，同步记录测点的加速度时程和位移时程。对经基线校正后的测点加速度时程进行积分，再与实测位移时程相对比，以讨论其可靠性。实验系统的组成和实验思路示意图如图6所示。

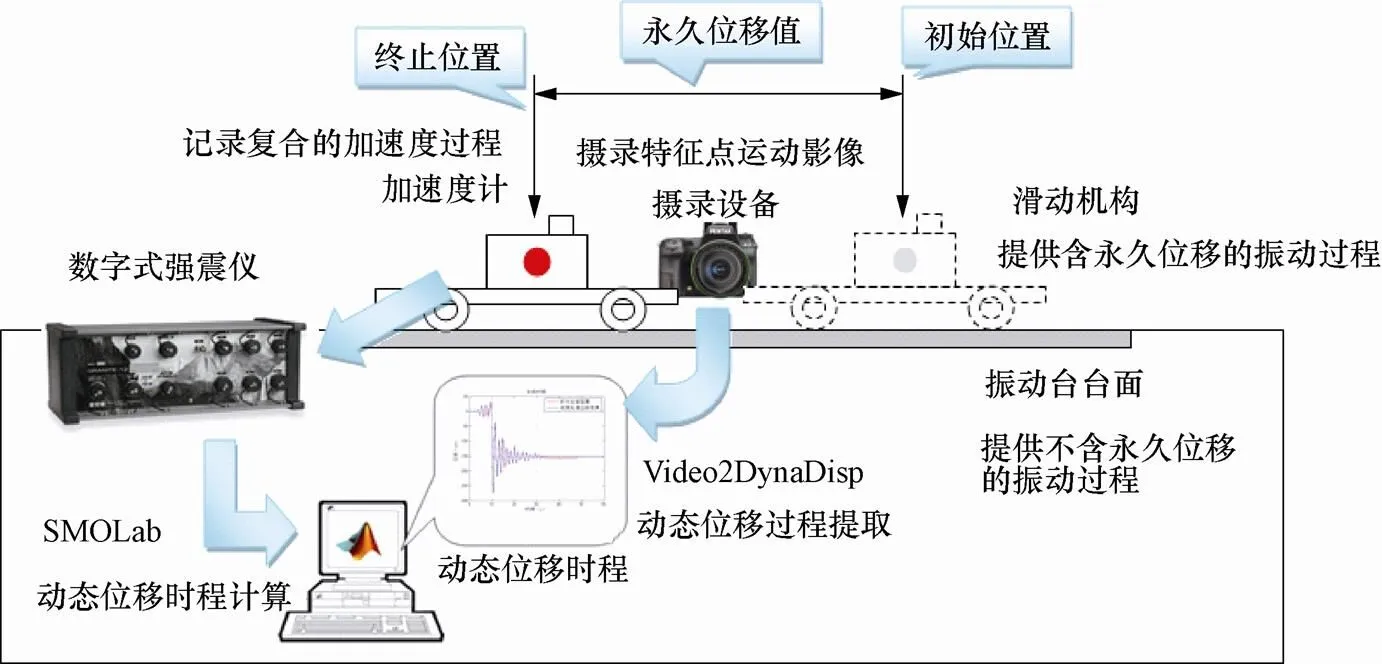
图6 实验系统组成和实验思路示意图

产生包含永久位移的振动过程是本实验系统的关键，该过程由图6和图7中所示的振动台和滑动机构组合作用生成。鉴于振动台本身在振动过程完成后会停留在位移为0的平衡位置，为了产生具有真实的永久位移的振动过程，本实验在振动台台面上安装了专门产生永久位移的滑动机构，其由固定在振动台台面上的直线导轨和能在导轨上滑动的平台组成，并由专门的弹簧驱动。在振动台开始运动前，滑动机构上的平台（用于安置加速度计）由人为拉离平衡位置，振动过程中释放平台让其在导轨上自由滑动，最终停止在弹簧控制的平衡位置。平台的起始位置和最终停留的平衡位置之间的距离就是实验工况中给定的永久位移值。

在本实验中滑动机构平台的加速度由强震动仪获取，振动台台面和强震动仪加速度计的动态位移数据采用本文提出的基于机器视觉的动态位移测量系统获取。振动台和滑动机构都为单向运动，采用“强震动观测辅助教学和数据处理系统（SMOLab）”进行加速度记录处理和积分，加速度基线校正方法及积分位移算法直接引用了王国权等（2003）提出的算法。

2.2 实验设计

实验在防灾科技学院地震模拟实验室的3m×3m双水平向振动台上进行，实验现场布置如图7所示。产生永久位移机构滑动的滑动导轨（图7中的C）紧固在振动台上，与振动台不会发生相对运动；产生永久位移的滑动平台（图7中的D）安置于滑动导轨上，只能沿导轨延伸方向做水平方向滑动，由端头分别固定在导轨两端和滑动平台的处于拉伸状态的两根弹簧产生滑动的驱动力。用来记录包含永久位移信息的加速度计固定在滑动机构上，并以白底红色标识点予以标识（图7中的A）。为了对比包含和不包含永久位移振动时程的差别，另在振动台台面上设置台面对照加速度计（图7中的B）。

实验中采用美国Kenimatrics公司的ES-T三分量力平衡式加速度计，灵敏度为2.5V/g，通频带为0—200Hz；记录器为美国Kinemetrics公司的12通道Granite型记录器，A/D转换单元为24位，动态范围为120dB，实验采样率取200sps；数字影像摄录设备为日本Pentax公司的K3数码单反相机，其具备2400万像素APC幅面CMOS传感器，摄录帧率为50帧/s。

图7 振动台实验现场工作照片

为了对比在不同峰值加速度和永久位移情况下由加速度时程确定位移时程和永久位移的可靠性，并减小其它因素的影响，本实验将考虑3档振动台台面加速度峰值输入水平、2档设定永久位移水平，具体设计如下：

（1）振动台激励选用El Centro地震动加速度记录作为母波，将输入加速度峰值调整到100cm/s2、200cm/s2和500cm/s2，振动台单向加载。

（2）设定施加永久位移为15cm和40cm，由滑动机构提供（人工施加振动状态，施加值以摄影测量值为准）。

3 实验数据处理和结果分析

按照前述处理方法对实验得到的6组典型数据进行处理和分析并得出相关结果。限于篇幅，本文仅给出了输入加速度峰值为200cm/s2、滑动机构产生40cm永久位移工况下的积分位移时程与直接量测位移的结果，如图8所示；图9给出了振动台峰值为500cm/s2、永久位移预设值分别为15cm和40cm工况下，直接量测位移时程和积分位移时程，以便对比分析输入加速度峰值较大的情况下2种设定施加永久位移的结果；同时，为了比对振动台台面位移时程，图8和图9中亦给出了固定在振动台台面上的加速度计的对应时程。

图8（a）—（d）中对应加速度时程为加速度计直接记录（未经或已经基线校正的），速度和位移值分别由加速度时程积分得到；图8（e）中位移时程由本文采用的基于机器视觉的动态位移测量方法直接测量得到。图9中台面位移时程为本文采用的基于机器视觉的动态位移测量方法直接测量得到的固定在台面上的加速度计运动的位移时程，不包含永久位移。

图8 振动台峰值加速度200cm/s2、永久位移40cm工况位移时程获取和基线校正结果

图9 积分校正位移时程和本文方法直接测得位移时程对比

图8和图9所示结果表明：

（1）采用现有的基线校正方法，加速度积分得到的位移时程与直接量测位移时程吻合较好。对比基线校正后积分得到的位移时程和本文直接测试得到的位移时程，在本实验室条件下，现有基线校正方法的结果是可以接受的，无论是否有永久位移条件下的加速度时程积分结果都是可以接受的。

（2）本实验中，不但得到的最终永久位移值可以接受，积分得到的整个位移过程也是可以接受的。

（3）本实验方法可以用来开展基线校正方法的可靠性和校正参数选择的有效性研究。

为了进一步对基线校正方法的计算精度进行讨论，本实验还对6个实验工况积分得到的最终永久位移和本文方法直接测得的永久位移进行了比较，并以本文方法直接测得值为基准计算了积分结果的相对误差，如表2所示。由表2可以看出，采用现有校正方法，所有工况都能得到可接受的永久位移值，实际上整个位移时程也都能够接受，限于篇幅不再详述。以本文方法直接测量永久位移值为基准，相对误差基本也能接受，均小于13%，尤其是永久位移大的情况下（40mm工况）效果更佳，相对误差控制在6%以内。

表2 永久位移15cm和40cm积分位移时程和视频处理位移时程尾值

4 结论

基于振动台实验及测试数据分析可以得到以下结论：

（1）本文提出的振动台实验方案能产生包含永久位移信息的振动过程，能较好地模拟记录永久位移测点的真实振动情况，能满足近场强震动记录基线校正方法的合理性验证和校正参数选择的有效性讨论的要求。

（2）采用现有基线校正方法校正后的加速度时程积分得到的位移时程是可以被接受的，包括最终的永久位移值和整个振动位移过程。

（3）在本实验条件下，现有校正方法得到的永久位移值的相对误差是可以接受的。

陈勇，陈鲲，俞言祥，2007．用集集主震记录研究近断层强震记录的基线校正方法．地震工程与工程振动，27（4）：1—7．

胡国瑞，2016．近场强震记录基线校正实验系统研究．北京：防灾科技学院．

黄蓓，2003．基于集集地震记录的近断层地震动特性分析．北京：中国地震局地球物理研究所，1—127．

王国权，周锡元，2004．9·21台湾集集地震近断层强震记录的基线校正．地震地质，26（1）：1—14．

于海英，江汶乡，解全才等，2009．近场数字强震仪记录误差分析与零线校正方法．地震工程与工程振动，29（6）：1—12．

周宝峰，2012．强震观测中的关键技术研究．哈尔滨：中国地震局工程力学研究所．

Boore D. M., 1999. Effect of baseline corrections on response spectra for two recordings of the 1999 Chi-Chi, Taiwan, earthquake. California：U. S. Geological Survey Open-File Report 99-545

Boore D. M., 2003. Analog-to-digital conversion as a source of drifts in displacements derived from digital recordings of ground acceleration. Bulletin of the Seismological Society of America, 93(5): 2017—2024.

Iwan W. D., Moser M. A., Peng C. Y., 1985. Some observations on strong-motion earthquake measurement using a digital accelerograph. Bulletin of the Seismological Society of America, 75(5): 1225—1246.

Trifunac M. D., 1971. Zero baseline correction of strong-motion accelerograms. Bulletin of the Seismological Society of America, 61(5): 1201—1211.

Wu Y. M., Wu C. F., 2007. Approximate recovery of coseismic deformation from Taiwan strong-motion records. Journal of Seismology, 11(2): 159—170.

卢滔，胡国瑞，何福，郭迅，霍敬妍，2017．近场强震动记录基线校正方法的振动台实验研究．震灾防御技术，12（3）：625—634．

Analysis on Baseline Correction Method of Strong Motion Accelerogram Recorded on Near-fault Site by the Shaking Table Test

Lu Tao, Hu Guorui, He Fu, Guo Xun and Huo Jingyan

(Institute of Disaster Prevention, Beijing 101601, China)

For determining the near-fault site permanent displacement in some specialized methods, near-fault accelerogram was corrected with baseline, and integrated into the displacement time history. The above result is often of uncertain and even not easy to be validated because of using the subjective parameters in process. To solve this problem, we proposed a shaking table test scheme to simulate the shake process including the permanent displacement. In the test, a system comprising the shaking table and the specialized sliding mechanism were used to model the actual shake situation on the site recorded the permanent displacement. The accelerogram was recorded by the accelerometer on the sliding mechanism, and the actual displacement time history was achieved on close-range photogrammetry. The displacement integrated by the accelerogram corrected the baseline was compared with the actual displacement to prove the reliability of the correction method. Our results show that the accelerogram could be integrated to the reliable displacement time history under the laboratory condition, after the baseline corrected with the specialized method.

Near-fault site; Strong motion accelerogram; Baseline correction; Permanent displacement; Shaking table test

10.11899/zzfy20170318

中央高校基本科研业务费专项资金创新团队资助计划项目（ZY20160110），地震科技星火计划项目（XH16002Y），国家自然科学基金（51208108）

2017-05-27

卢滔，男，生于1979年。博士，副教授。主要从事工程地震理论和应用研究。E-mail：lutao@cidp.edu.cn