一种新型椭圆齿轮马达的动力学分析
2018-01-19李殿起陈平亮刘光辉
魏 爽,李殿起,陈平亮,刘光辉
(沈阳工业大学机械工程学院,辽宁 沈阳 110870)
0 前言
非圆行星齿轮液压马达是一种新型的液压马达,具有结构紧凑、抗污染能力强等特点,已成为近年来马达研究的一个新方向[1]。武丽梅综述了非圆齿轮技术的发展及应用[2];熊镇芹研究了非圆齿轮马达的配流特性,计算了配流孔的个数及配流面积[3];许鸿昊提出了阶梯型设计内齿圈、行星轮及太阳轮厚度的方法,以提高马达的总效率[1],但以上都局限于对低阶非圆齿轮马达的研究。本文提出一种高阶非圆齿轮马达:6-8阶椭圆齿轮马达,研究了该马达中椭圆齿轮系统的动力学特性,并分析了振动响应。为非圆齿轮马达应用过程中合理的确定动态系数来满足工程要求提供了依据。
1 6-8阶椭圆齿轮马达的工作原理及结构
1.1 椭圆齿轮马达的工作原理
6-8阶椭圆行星齿轮马达由6-8阶椭圆行星齿轮机构、马达壳体、配液装置、动力输出装置、密封系统等组成。马达壳体外侧有两条进排液管道,通过液压软管与换向阀相连,内侧设有进排液孔[4],与椭圆行星齿轮机构中相邻的两个行星轮形成密闭容腔。其中,椭圆齿轮系统是由节曲线分别是6阶椭圆的太阳轮和8阶椭圆的内齿圈以及圆柱行星轮组成的。由于相邻两行星轮的中心夹角是变化的,因此椭圆行星齿轮马达没有行星架,依靠齿轮之间的啮合力运转,既液压油推动行星轮旋转,太阳轮通过连轴钢球与动力输出轴相连,在行星轮的啮合作用下,输出动力。图1是6-8阶椭圆行星齿轮马达中行星轮系统的结构。

图1 6-8阶椭圆行星齿轮马达行星轮系统的结构
1.2 椭圆行星齿轮机构中太阳轮及内齿圈的节曲线
在椭圆行星齿轮机构中,令行星轮的公转角速度为0,那么太阳轮和内齿圈分别以W1、W3的角速度转动,行星轮在以角速度W2自转的同时,还要沿中心连线方向做平移[5]。令行星轮与内齿圈及太阳轮节曲线的瞬时切点分别为C、D两点,由三心定理可知,轮系中心0与C、D三点是共线的[6]。图2是非圆齿轮机构的运动关系简图。

图2 非圆齿轮轮系运动关系
椭圆太阳轮的极坐标方程为[5]
(1)
令D点的节曲线切线正向与向径rs的夹角为μ1,则
(2)
内齿圈的节曲线方程为
(3)
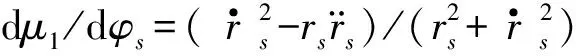
为保证马达能正常工作,椭圆行星齿轮系统的节曲线需要满足以下条件:

(3)不发生干涉的条件,即太阳轮最大向径处的齿顶与内齿圈最小向径处的齿顶不会碰撞[7]。
给出不同的Ns、Nr、模数m,行星轮齿数zp,由以上方程就能得到相应的RZ和e,从而得到椭圆齿轮系统中各齿轮的节曲线。图3是取m=1时,得到的6-8阶椭圆齿轮的太阳轮和内齿圈的节曲线。

图3 6-8阶椭圆齿轮的节曲线
1.3 太阳轮及内齿圈的齿廓
对于节曲线有内凹的非圆齿轮,需要用产形齿轮与非圆齿轮内、外啮合来设计非圆齿轮的齿廓,其中产形齿轮基圆的切线是产形齿轮与啮合齿轮的瞬时啮合线[6]。本文介绍一种借助MATLAB计算语言由太阳轮的节曲线参数插值得到内齿圈齿廓的方法。

(4)
在静坐标系o1x1y1中,Fs点的直角坐标为[6]
(5)
其中,x2s、y2s是Fs点在坐标系o2x2my2m中的坐标;β1是过C点的竖直线与直线O2C之间的夹角;x102、y102是产形齿轮的中心在静坐标系o1x1y1中的坐标。
式(1)~(3)用极坐标的方法,由太阳轮的节曲线,得出了内齿圈的节曲线,而式(5)是直角坐标的形式,因此可以用三样条插值法把极坐标转换成直角坐标:将太阳轮的转角φs分成若干等分,并找到内齿圈瞬时极角φr对应的相邻的四个太阳轮转角,采用插值的方法,拟合可得到这四个太阳轮转角对应的内齿圈极径的公式。
令产形齿轮的半径为r2,则产形齿轮的中心在静坐标系o1x1y1中的坐标为
(6)
其中r2是产形齿轮的节圆半径。通过式(6)可把极坐标转换成直角坐标表示,把式(6)带入式(5)便可得到Fs点的直角坐标。Fs点的坐标是关于转角t1的参数方程,当t1由小变大时,将动坐标系o2x2my2m和静坐标系o1x1y1进行坐标转换,啮合点在内齿圈的齿廓上,由齿顶运动到齿根部,即得到了内齿圈的顺时针齿廓,内齿圈的逆时针齿廓及太阳轮的齿廓是用类似的方法得到的。图4是已知太阳轮的节曲线公式通过插值法得到的内齿圈的齿廓,由于内齿圈节曲线的曲率时刻变化,导致内齿圈的各个齿廓的形状也各不相同[7]。

图4 由插值法得到的内齿圈齿廓
2 6-8阶椭圆行星齿轮系统的动力学分析
2.1 椭圆行星齿轮系统的运动规律
找出各参数随太阳轮转角的变化规律,能为齿轮动力学研究提供方向。图5~7分别绘制了太阳轮的极径、内齿圈的转角及内齿圈的角速度随太阳轮转角的变化规律。
由图5~7看出,太阳轮的极径随着转角时刻变化,导致太阳轮与行星轮外啮合的中心矩以及太阳轮的当量圆齿轮的转动惯量是时变的。由于非圆齿轮每个齿廓的形状各不相同,导致啮合角时刻变化;以太阳轮为参考,内齿圈的角速度是波动的,导致太阳轮转角为φs时,行星轮的转角不等于φs/(Ns+Nr),而是在其上下波动 。非圆行星齿轮系统的动态特性比圆柱行星齿轮系统的动态特性复杂,因此,需要对非圆行星齿轮的动力学特性进行分析,以减小非圆行星齿轮系统在实际应用中的振动及噪声。

图5 太阳轮的极径与太阳轮转角的关系
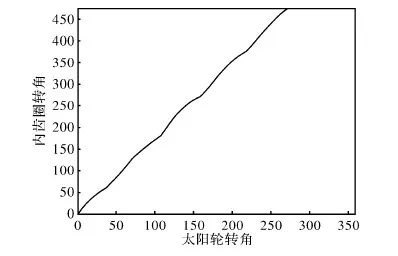
图6 内齿圈的转角与太阳轮转角的关系

图7 内齿圈的角速度与太阳轮转角的关系
2.2 6-8阶椭圆行星齿轮的动力学模型及分析
6-8阶椭圆齿轮系统产生振动的因素除了包括轮齿动态激励,如:齿轮本身的结构形式、几何特性及误差等,还包括动态啮合力等。因此原则上必须从整个行星齿轮系统出发,建立齿轮的振动分析模型。本文假定齿轮传动轴、支撑轴承和马达壳体的支撑刚度足够大,可不考虑它们的弹性,并且输出轴的刚度较小,可将行星齿轮系统与原动机隔离,从而单独建立齿轮系统的纯扭转振动模型。图8是基于以上条件建立的椭圆行星齿轮系统的力学模型。

图8 椭圆行星齿轮系统的力学模型
由于椭圆行星齿轮内、外啮合的传动比是时刻变化的,在每一瞬时,都可以将椭圆太阳轮和内齿圈等效成各自瞬时半径对应的圆齿轮。那么在任意时刻椭圆齿轮的动力学模型也可以由节圆半径分别为rs、rr的圆柱太阳轮和圆柱内齿圈替代,然后利用逐段线性近似法[8]求出整个系统的振动响应。首先,将每个回转周期划分成微小的时间段[9],采用数值解法来分析微小时间段内椭圆行星齿轮的振动模型。
定义内外啮合线上的相对位移Xrdi及Xsdi为
(7)
则微小时间段内非圆行星齿轮副啮合传动的振动方程为
(8)
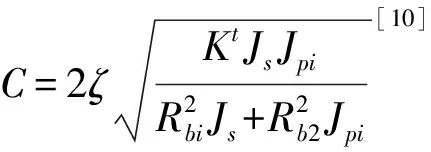
为转矩的等效力;J为转动惯量;Rb为瞬时当量齿轮半径;Ms为太阳轮的当量质量;Mpi为单个行星轮的当量质量。
扭转振动模型可用矩阵表示为[11]

(9)

(10)
式中,Km为刚度的平均值;Kpic、Kpis分别为啮合副时变啮合刚度的余弦系数及正弦系数[12]。
啮合时间
(11)



图9 行星轮直径与太阳轮转角的关系
当确定负载转矩后,根据转矩关系及与各个行星轮啮合的太阳轮的瞬时当量半径,就可以确定PL、PDi。以上分析将动力学模型中随集中转动惯量的转角变化的参数(振动产生的根本因素):刚度K、阻尼C及转矩等效力P确定了。
2.3 动力学方程的求解
对于非线性方程组,可以利用龙格库塔方法进行求解,得到其数值解。以模数m=2的6-8阶椭圆行星齿轮为算例,该齿轮系统的参数为:齿数Zs=78,Zpi=12,Zr=104,齿宽b=20 mm,压力角∂=20°,齿轮副侧隙bps=bpr=30 μm,阻尼比系数ζ=0.04,太阳轮的转速ns=180 r/min,啮合综合误差espi=erpi=2 um,输出转矩T=80 N·m,外啮合平均刚度Kmsp=0.556 98 GN/m,内啮合平均刚度Kmrp=0.534 82 GN/m。
图10是该椭圆齿轮系统的速度响应,图11是位移频率谱。

图10 速度响应
由图10及图11看出,在以上给定的参数下,椭圆行星齿轮系统的位移响应不像圆柱行星齿轮系统那样,最大幅值并不在啮合频率及倍频处,但内外啮合振动的最大幅值出现在同一频率处。

图11 位移频率谱
3 结论
(1)提出了一种新型的低速大扭矩马达即6-8阶椭圆齿轮马达, 相比于现有文献中研究的非圆齿轮马达,该类型马达的排量大、效率高,同时由于结构相对复杂,导致动态特性较差。
(2)椭圆行星齿轮马达由液压油推动行星轮来输入动力,太阳轮连接输出轴输出动力。行星轮与太阳轮的转角关系及行星轮的啮合相位差不同于普通圆柱行星齿轮,导致椭圆行星齿轮系统的动力学方程与普通圆柱行星齿轮不同,文中给出的动力学方程及求解方法适用于任何类型椭圆行星齿轮系统,从而为椭圆行星齿轮马达的振动分析提供了理论依据。
[1] 许鸿昊,张华,沈银杰.非圆行星齿轮液压马达总效率的提高[J].液压与气动,2014(04):80-84.
[2] 武丽梅,鲁墨武.非圆齿轮技术的发展及应用[J].沈阳航空工业学院学报,2000,17(01):23-26.
[3] 熊镇芹,吴序堂,高本河.非圆行星齿轮液压马达参数设计[J].机床与液压,2004(05):50-51.
[4] 非圆齿轮行星轮系低速大扭矩液压马达[P].
[5] 吴序堂,王贵海.非圆齿轮及非匀速比传动[M].北京:机械工业出版社,1997.
[6] 姚文席.非圆齿轮设计[M].北京:机械工业出版社,2013.
[7] Bair B W.Computer Aided Design of Elliptical Gears[J].Journal of Mechanical Design,2002,124(12):787-793.
[8] 杨叔子,杨克冲.机械工程控制基础[M].武汉:华中科技大学出版社,2002.
[9] 王雷.非圆齿轮动力学特性研究[D].郑州:郑州大学,2008.
[10] 孙智民,季林红,沈允文.2K-H行星齿轮传动非线性动力学[J].清华大学学报(自然科学版),2003,43(05):636-639.
[11] 叶福民.非等模数非等压力角行星齿轮传动系统设计与动力学特性研究[D].南京:南京航空航天大学,2014.
[12] 肖正明.土压平衡盾构机主减速器三级行星齿轮系统动力学[D].重庆:重庆大学,2011.
